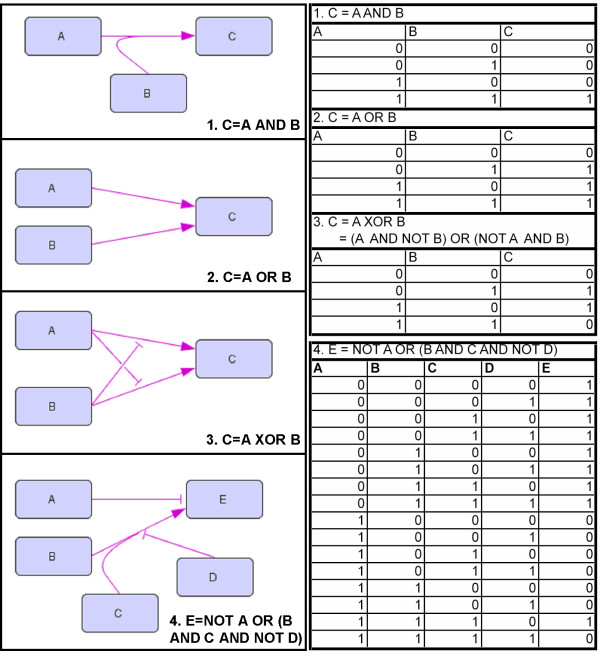
Figure 2.

Example of Boolean expressions and corresponding logical hypergraphs and truth tables. A logical hypegraph is an interaction network where each edge (or hyperarc) connects a set of start-nodes (tails) to an end-node (head), and the combination of incoming hyperarcs to an end-node represents a Boolean expression. Any Boolean expression can be written in a disjunctive normal form (only using AND, OR and NOT operators). On the disjunctive normal form, expressions are built up by literals (i.e. variables or their negation) connected by AND relations forming clauses, and clauses can then be connected by OR relationships. In the logical hypergraph, each clause is represented by a hyperarc, while separate hyperarcs linked to an end-node represents clauses connected by an OR relationship. When the value of a tail species is negated, this is marked by a repression symbol in the corresponding hyperarc (see also the symbolic explanation in Figure 3). The Boolean function determining the state of a node is thus given by all the incoming hyperedges.