Development of a Novel Post-processing Treatment Planning Platform for 4D Radiotherapy

Abstract

The aim of this study is to develop an Automatic Post-processing Tool for four-dimensional (4D) treatment planning (APT4D) that enables the user to perform some necessary procedures related to 4D treatment planning, such as automated image registration, automatic propagation of regions of interest, and dose distribution transformation. Demons-based deformable registrations were performed to map the moving phase images (such as the end-inhalation phase or 0% phase) to the reference phase (typically the end-exhalation fixed phase or 50% phase). Contours were automatically propagated into the moving phase using the image registration results. The dose distribution of each moving phase was transformed to the fixed phase and subsequently was summed as an average with equal weighting factor. To validate the application of APT4D utility, the 4D computed tomography (CT) images of a lung cancer patient and an abdominal cancer patient were acquired and resorted into ten respiratory phases. 4D plans based on the 4D CT images were developed. The correlation coefficient ranged from 0.992 to 0.999 for the re-sampled deformed moving phase image against the fixed phase image for the lung patient plan and from 0.977 to 0.999 for the abdominal patient plan. For all the organs, the match indices between the manual contours and automatic contour propagation results were around 0.92 to 0.95. The 4D composite dose-volume histogram showed dosimetric reductions for liver and kidneys in the high dose region. The APT4D adds automation, efficiency, and functionality, while integrating the whole process of 4D treatment planning.

Introduction

The goal of modern radiotherapy treatment methodologies, such as intensity-modulated radiation therapy (IMRT) and stereotactic body radiation therapy (SBRT), is to treat the tumor with more conformity, and possibly higher dose, while sparing the normal structures and yielding improved local control and survival (1). To achieve this goal, accurate patient setup and precise geometric knowledge of the target volume are needed for treatment planning and treatment delivery. Variations in patient setup can be minimized with the help of immobilization devices and patient positioning systems. However, internal organ motion, both inter-fractionally and intra-fractionally, limits the dosimetric accuracy of the treatment and presents a challenge. Inter-fractional motion occurs when the clinical target volume (CTV) changes on a daily basis and is a result of tumor growth or shrinkage, weight loss or gain, daily bowel and bladder filling, and radiation induced change of tissue. In clinical practice, the acquisition of computed tomography (CT) images just prior to the treatment could be used to adjust and verify the daily location of the CTV. Additionally, so-called “adaptive” radiotherapy offers the ability to account for the inter-fractional motion (2). Intra-fractional motion on the other hand, occurs while the patient is being irradiated. It is caused by motion due to the patient’s respiratory, skeletal muscular, cardiac and gastrointestinal systems. Of these systems, respiration-induced motion is the most significant and one that has the highest impact in radiation therapy. Respiratory motion can introduce significant errors in imaging (3–9), treatment planning (9–11), and treatment delivery (12–15). In current radiotherapy treatment practice, the respiratory motion is typically accounted for by adding uniform, population-based margins to the CTV in order to obtain the internal target volume (ITV) (1), often resulting in undesirably higher doses to unnecessarily exposed normal tissue.

The development of 4D imaging technology brings us to the era of 4D radiotherapy, which allows us to capture and utilize the temporal changes in anatomy during the imaging, planning, and delivery of radiotherapy. Acquiring 4D images (three spatial dimensions + phase) offers the capability to track the patient’s respiratory motion with a reduction in motion artifact. This facilitates the more accurate delivery of treatment, especially in the abdomen and thorax. These images enable 4D treatment planning, reflecting the realistic motion of the target that allows for reduction of the ITV margin. In theory, the concept of 4D planning is intuitive; however, in practice it is very complex because of the expanded amount of image data (10~20 times more image data than a standard planning scan) (7). In principle, the work flow of 4D planning involves automated image registration, automatic propagation of regions of interest (ROIs) between phases and dose distribution transformation. Several investigators have published their efforts to implement 4D treatment planning through specific aspects of the 4D planning procedure (16–19). However, a robust solution for 4D treatment planning is not yet widely available. The need for the automation tools that can perform the necessary tasks and reduce the workload is clear to all (20). Logistically, performing all of the 4D planning tasks manually on such a large volume of CT images would necessitate significant human interaction time. Although manual contouring slice by slice is reliable, it is too time-consuming and labor-intensive to be used routinely. To add the dose mathematically from different phases, a process of dose transformation to the same physical space and coordinate system is necessary.

In this study, we have constructed an Automatic Post-processing Tool for 4D treatment planning (APT4D) that allows deformable image-based registration. Additionally, we perform automatic contour deformation and propagation between different imaging phases and 4D dose summation. The APT4D is a post-planning tool since it depends on the output from a commercial three-dimensional (3D) treatment planning system (TPS), requiring data such as contours and dose calculation matrix. In the following sections, the functionality and clinical application of APT4D are described and tested for one lung cancer patient and one abdominal cancer patient since the respiratory motion gives a special challenge to the case of thoracic and abdominal tumors compared to tumors at the other sites of the body. It is important to note that APT4D is a proof-of-principle at current stage rather than a clinical tool.

Materials And Methods

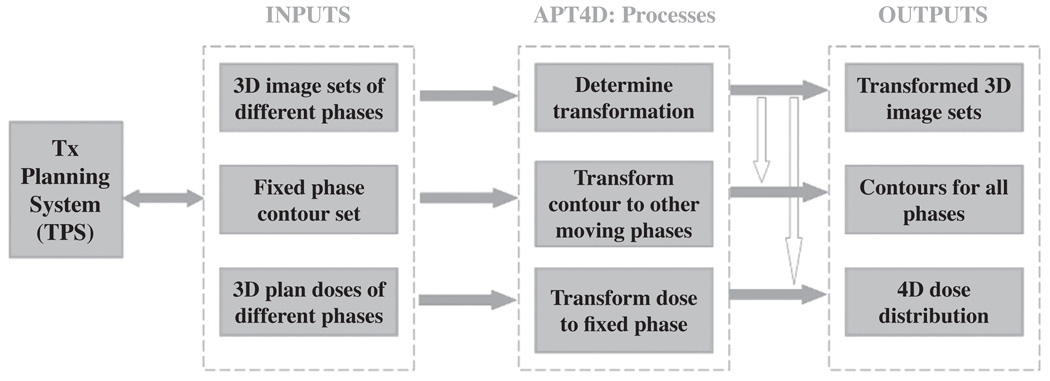
The graphical user interface (GUI) of APT4D was developed to facilitate the generation of a 4D plan. The interface was constructed using Matlab 6.5 (The MathWorks Inc., Natick, MA, 01760, USA). The rigid registration algorithm and non-rigid demons deformable registration algorithm were implanted on the open source Insight Toolkit (ITK, www.itk.org/) and implemented in C++ programming language. The code was compiled as the executable file to be called in APT4D. The data flow chart between APT4D and the TPS is illustrated in Figure 1. The three dashed blocks represent, respectively, the input to APT4D, the functionality of APT4D, and the output from APT4D. It is important to note that, APT4D is not designed for a specific TPS although currently APT4D has been tested and implemented in our institution in two commercial TPS (Pinnacle³, Medical Systems, Milpitas, CA; Corvus, North American Scientific, Chatsworth, CA).

Figure 1.

Flow chart of integration of APT4D and TPS.

As seen in Figure 1, the inputs into APT4D include 3D image sets of different phases, one contour set manually delineated on the fixed (reference) phase, and dose matrices calculated for different phases. APT4D performs three major tasks: (i) non-rigid deformable registration, which determines the transformation mapping between the fixed phase image and each of the moving phases images; (ii) contour propagation, which transforms contours of the fixed phase to all the moving phases; (iii) dose transformation, which maps voxel-based dose information from the moving phases back to the fixed phase. The output of APT4D can be exported back to TPS to finalize the plans for 4D delivery.

Image Acquisition

The images for a non-small cell lung cancer patient and a pancreatic caner patient were acquired on a multislice CT scanner (Lightspeed QX/I 4-slice scanner, GE Medical Systems, Milwaukee, WI) in axial cine mode with quiet, free breathing. During the scanning, respiratory motion information was acquired by monitoring the position of the anterior abdominal surface (Real-time Position Management, RPM, Varian Medical Systems, Palo Alto, CA). The reconstructed axial images and RPM respiratory data were retrospectively sorted into ten respiratory phase bins using a commercial software package (Advantage 4D CT application software package, GE Medical Systems, Milwaukee, WI). Data sets were labeled by the percentage of the respiratory cycle, with 0% corresponding to end-inhalation and 50% corresponding to end-exhalation. The 50% phase was assigned as the fixed phase (reference phase) in this study since this phase was generally considered as the most reproducible phase (21). To reduce the memory burden, images were down-sampled to a size of 256 × 256 with a pixel resolution of 1.96 × 1.96 mm², while keeping the same cranial-dorsal direction resolution of 2.5 mm.

Image Registration

The local deformable registration from the moving phase to fixed phase was performed using the demons method. This method was derived from the algorithm by Thirion (22). It was inspired by the concept of optical flow and was initially used in computer vision research. The algorithm was based on the concept of diffusing models to perform image matching through the movement of a deformable grid through a semi-permeable contour of an object surface in the other image. Each object surface in the image is defined by pixels on its boundary contour, so called “demons”. The diffusion model assumes the “demons” at each voxel from the fixed image are applying forces that push the voxels of the moving image m into the matched fixed image f. Iteratively, as the model approaches the final convergence, the forces applied gradually decreases. The displacement between the fixed and moving images was derived by Eq. [1]: (22)

$$\overrightarrow{\mathrm{D}}=-\frac{(m-f)\overrightarrow{\nabla }f}{\left|\right|\overrightarrow{\nabla }f|{|}^2+{(m-f)}^2/k}$$ [1]

where ∇⃗ f represents the relationship between the neighboring points in the fixed image, k is the normalization factor that accounts for the units imbalance between intensities and gradients, D⃗ stands for the displacement or optical flow between the images, and the (m−f) means the differential force of the interaction between the images. The above equation was iteratively calculated with a Gaussian filter smoothing the deformation field between iterations. Typically, a total of 150 iterations were to be sufficient in our implementation in order to obtain optimal convergence.

The evaluation of the performance for image registration is without any generally recognized “gold standard”. Both subjective and objective evaluation methods were applied to assess the behavior of the registration results. The subjective examination was qualitative. The transformed images were either exported back to the TPS for visual inspection or visually checked at APT4D. A subtraction image between the fixed phase images and deformed moving phase images was computed to assess the deformation and registration operation. The quantitative evaluation involves the similarity measurements between the two images. The normalized correlation coefficient of two images at each slice was calculated using Eq. [2]:

$$r=\frac{{\displaystyle \sum _m{\displaystyle \sum _n(A_{mn}-\overline{A})}(B_{mn}-\overline{B})}}{\sqrt{({\displaystyle \sum _m{\displaystyle \sum _n{(A_{mn}-\overline{A})}^2}(\sum _m\sum _n{(B_{mn}-\overline{B})}^2})}}$$ [2]

Here, A and B were the image intensities and A̅ and B̅ were the mean intensity of the two images, respectively. If the two images are identical, the correlation coefficient is equal to 1. The closer the value to 1, the better the image registration result. It is important to note that APT4D can be extended to other registration algorithms, although currently only the demons method is implemented.

Automatic Contour Propagation

The deformable registration-based contour propagation method was applied in APT4D. The contouring of region of interests (ROI) for the fixed phase was performed using the Pinnacle³ TPS. A series of discrete transverse contours that were represented by a list of vertices for ROIs at the fixed phase were imported into APT4D. Since Matlab offers the ability to handle images as a matrix operation, the planar parallel contours were reconstructed as the 3D binary mask image data that has zero value outside of the 3D outline of ROIs. A user assigned image pixel value (also treated as organ identification) was assigned to each ROI for future identification. The imported ROIs were then transformed with the displacement map from the image registration result into other phases. Each new ROI was identified and extracted as a contiguous chain of coordinates for the closed contour. The performance of the contour propagation was evaluated by visually comparing the manual contours, and by quantitatively calculating the matching index. The matching index was defined as the ratio of the intersection percentage of the volume between the automatic contour propagation and the manual contouring to the union of the two volumes, and is given in Eq. [3]. If the contour propagation is identical to the manual contour, the match index is equal to 1. When the contour propagation does not have any intersection, the match index is 0.

$$\mathit{\text{math index}}=\frac{\mathit{\text{contour propagatio}}\cap \mathit{\text{manual contour}}}{\mathit{\text{contour propagatio}}\cup \mathit{\text{manual contour}}}$$ [3]

Dose Transformation

The 3D dynamic MLC (DMLC) based IMRT treatment plans were generated for 0% and 50% respiratory phase for both patients. The lung cancer patient plan used five beams (each at gantry angles: 130°, 180°, 230°, 280°, 330°). The seven beams (each at gantry angles: 30°, 80°, 130°, 180°, 230°, 280°, 330°) were used for the pancreatic cancer patient plan. Each phase of the IMRT plans produced deliverable step-and-shoot beams at the completion of the optimization with the same parameters. The dose matrix for the 0% phase plan was transformed to the 50% phase via the matrices obtained from the deformable image registration. The final combined 4D dose distribution was calculated on APT4D with an equal weighting factor for each phase. Although, an equal weighting factor was utilized, different weighting factors may be required for the optimization of 4D treatment planning.

Results

Image Registration

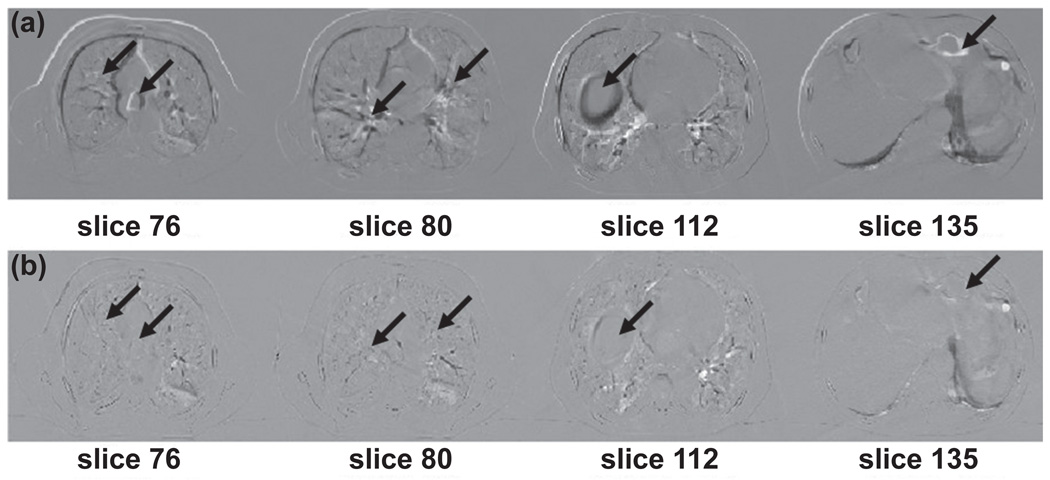
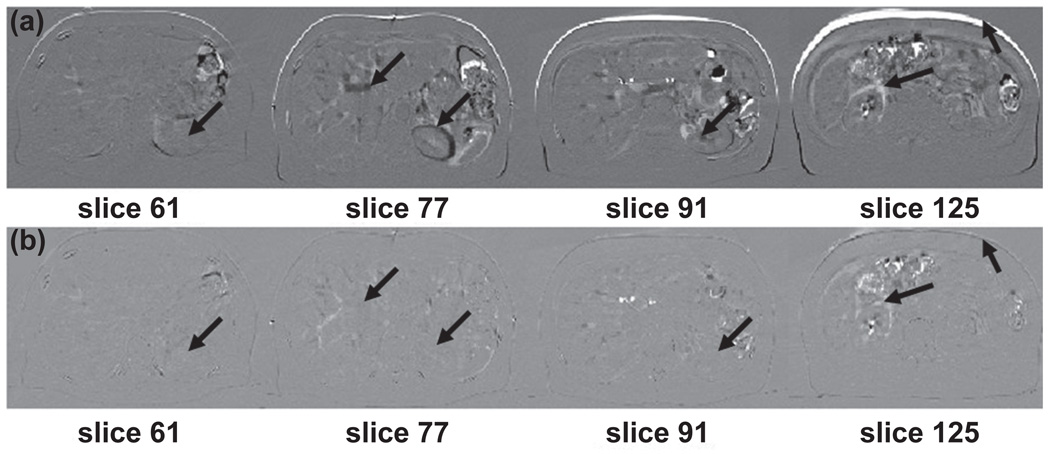
Figure 2 illustrates the subtraction (difference) images in axial view for CT volumes before and after image registration at the 0% and 50% phases for the lung cancer patient. The top row (a) shows the subtraction of images at different slices before deformable registration. The bottom row (b) displays the subtraction of images at different slices after deformable registration. Arrows indicate the regions where differences in pre and post registration are observed. The registration results for the abdominal cancer patient are shown in Figure 3. A large anatomic change was apparent between the two peak respiratory phases. Visually inspection of the performance of deformable image registration indicates most of the motion was mapped correctly by the demons registration.

Figure 2.

Difference slices of images for pre and post image registration of end-inhalation and end-exhalation 4D CT volumes for lung cancer patient. Top row: subtraction images before image registration. Bottom row: subtraction images after image registration. Arrows indicate structures where differences are observed.

Figure 3.

Difference slices of images for pre and post image registration of end-inhalation and end-exhalation 4D CT volumes for abdominal cancer patient. Top row: subtraction images before image registration. Bottom row: subtraction images after image registration. Arrows indicate structures where differences are observed.

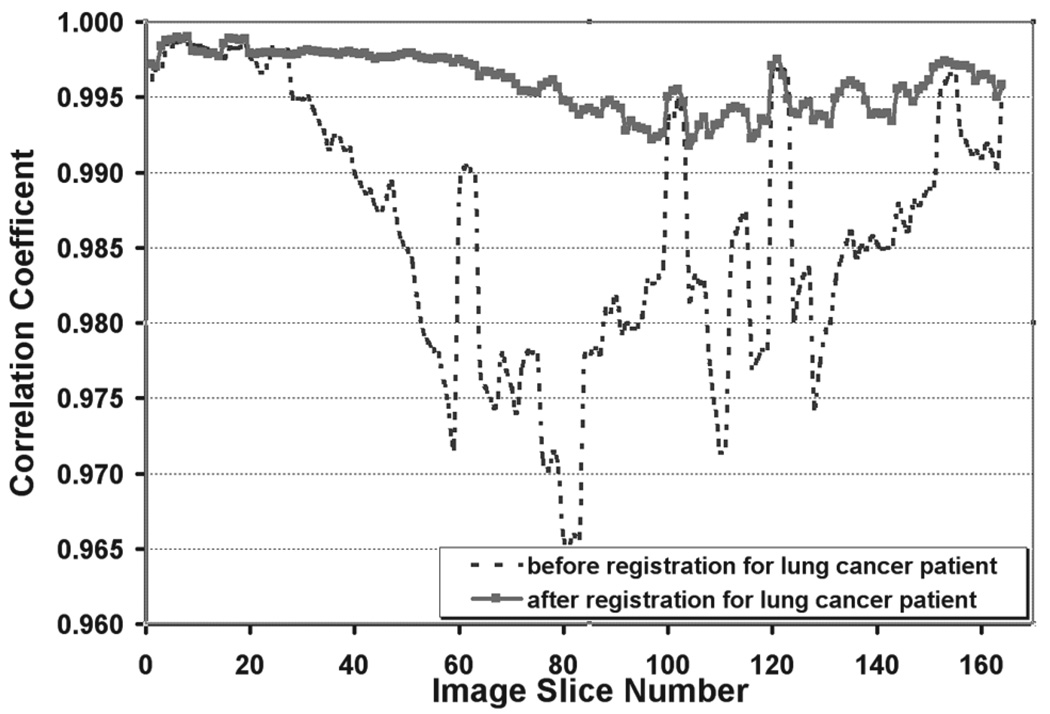
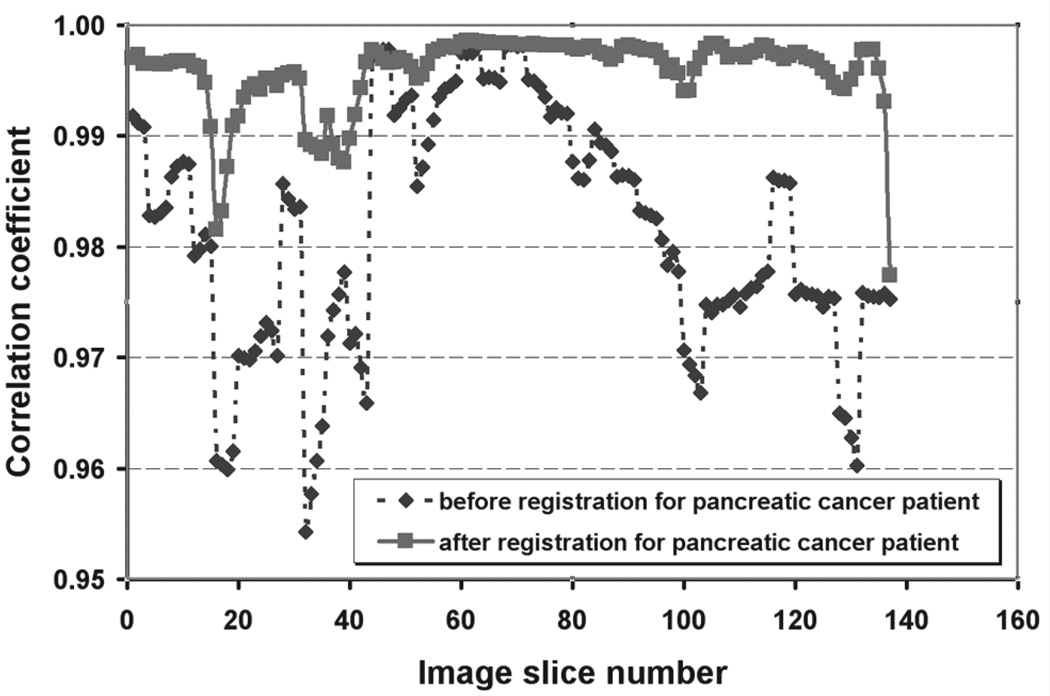
The quantitative validation for image registration is shown in Figure 4 and Figure 5. Figure 4 plots the correlation coefficient as a function of the image slice numbers before and after deformable registration for the lung cancer patient. Figure 5 shows the correlation coefficient for the abdominal cancer patient. The correlation coefficient ranged from 0.992 to 0.999 for the resampled deformed moving phase image against the fixed phase image for the lung patient and from 0.977 to 0.999 for the abdominal patient.

Figure 4.

Correlation coefficient calculated before and after image registration of end-inhalation to end-exhalation 4D CT volumes for the lung cancer patient. The dashed line represents the correlation coefficient before image registration. The solid line with the square represents the correlation coefficient after image registration.

Figure 5.

Correlation coefficient calculated before and after image registration of end-inhalation to end-exhalation 4D CT volumes for the abdominal cancer patient. The dashed line with the diamond represents the correlation coefficient before image registration. The solid line with the square represents the correlation coefficient after image registration.

Contour Propagation

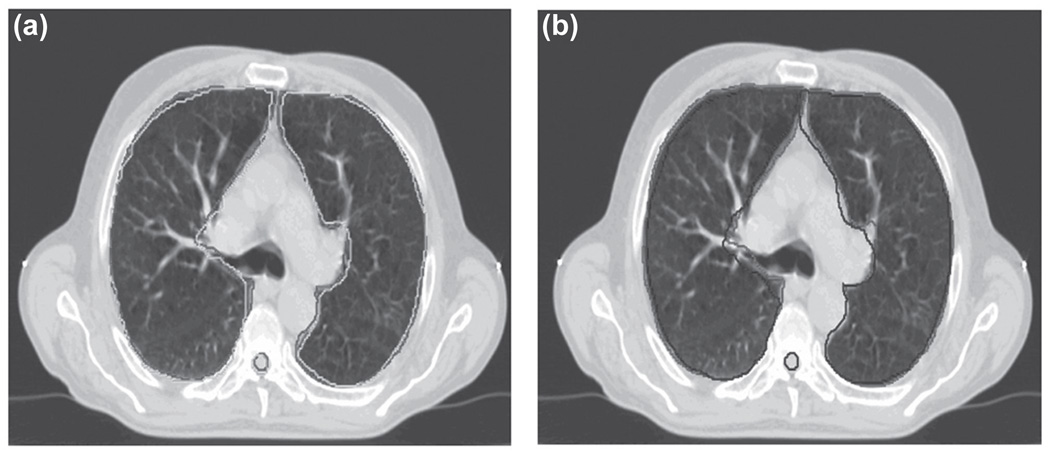
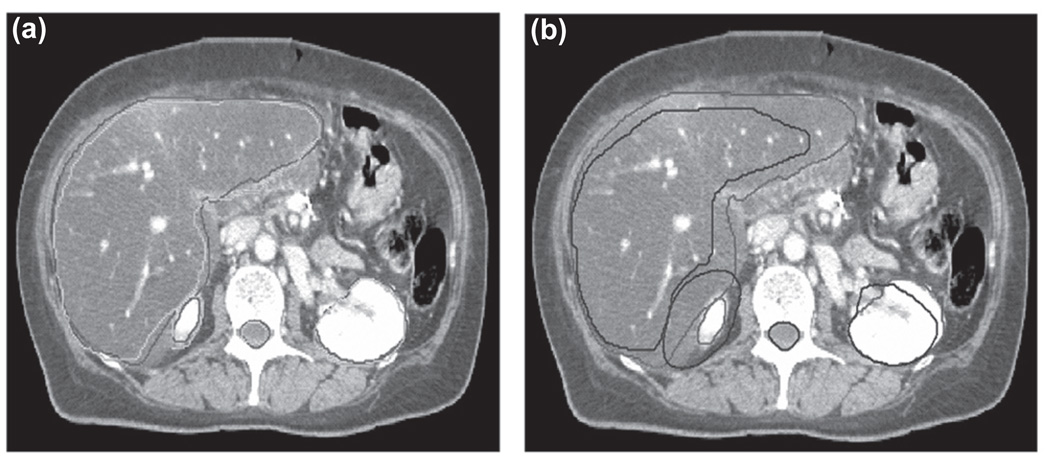
The 50% phase manual contour was used as the reference contour. The 3D binary mask contour image at the 50% phase was deformed to the 0% phase. Figure 6a shows the 0% phase CT image of the lung patient with its associated manual contours. The manual contours for the 50% phase CT image are included for comparison in Figure 6b. Figure 7a compares the automatic contour propagation results with the manual contours for the 0% phase superimposed on the 0% phase CT image. Figure 7b shows the manual contours for the 0% phase and 50% phase overlaid on the 0% phase CT image. It is evident that both the liver and kidneys have large deformation due to respiratory motion. The implementation of automatic contour propagation provides a much improved and efficient way to complete the tedious contouring work for multiple scanning phases, even though some contouring editing may still be necessary on some slices.

Figure 6.

(a) Comparison of automatic contour propagation results (green) and the manual contour (red) for lung patient superimposed on the end-inhalation phase CT image. (b) Manual contour on the end-inhalation phase (red) vs. manual contour on the end-exhalation phase (blue).

Figure 7.

(a) Comparison of automatic contour propagation results (green) and the manual contour (red) for abdominal patient superimposed on the end-inhalation phase CT image. (b) Manual contour on the end-inhalation phase (red) vs. manual contour on the end-exhalation phase (blue).

The match indices between the manual contours and automatic contour propagation results for the two extreme respiratory phases are summarized in Table I. The anatomic change and deformation for the lung patient case is relatively smaller than that for the abdominal patient case. The match indices for the lungs between two manual contours on two peak phases are around 89%. While the matching between the manual contours for liver and kidneys are relatively poor (less than 80%). For all the structures, the match indices between the manual contours and automatic contour propagation results are increased at least 5% and up to 21%. This increase demonstrated that the automatic contour propagation algorithm based on the deformable image registration can match the contours to the real data very well.

Table I.

Contour match indices for different organs.

	Left lung	Right lung	Liver	Left kidney	Right kidney
Phase0 manual contour vs. Phase5 manual contour	0.89	0.89	0.71	0.80	0.76
Phase0 manual contour vs. automatic contour propagation	0.94	0.95	0.92	0.93	0.92

Dose Transformation

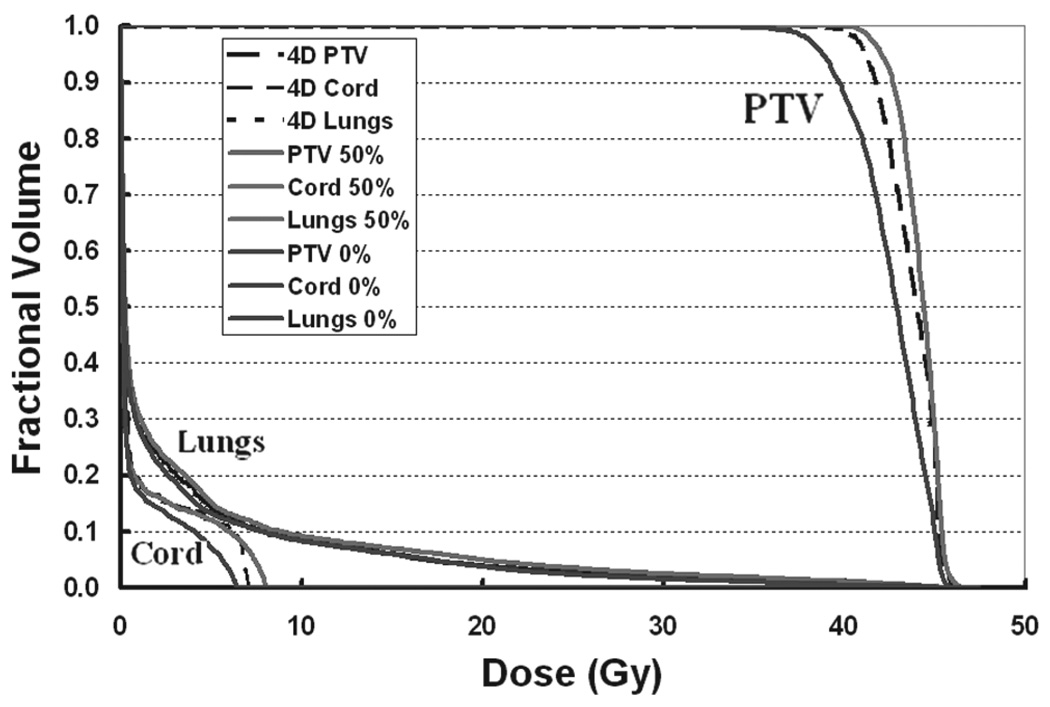
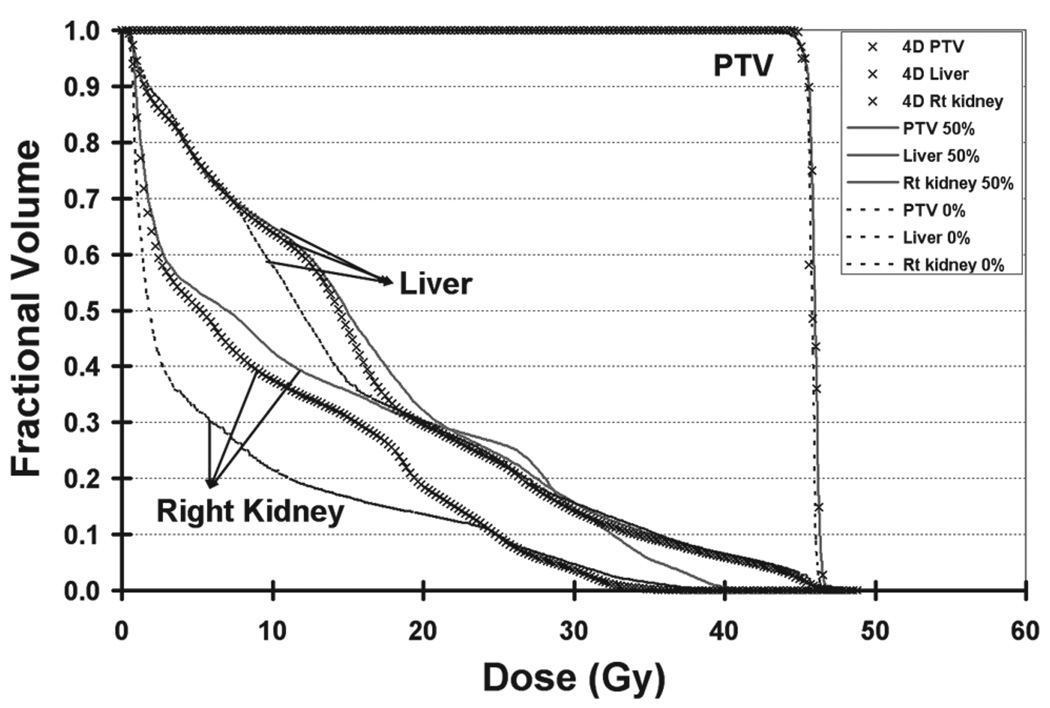
Comparison of the dose volume histograms (DVH) among the 0% phase plan, 50% phase plan and 4D plan are given in Figure 8 for the PTV, cord and total lung. The DVHs for the total lung were closely bunched. The 4D composite DVH for PTV and spinal cord appeared to be around the middle of each phase DVHs and tended to be closer to the 50% phase DVH. The DVH for 0% and 50% phase plan and the 4D plan for the PTV, liver and kidneys are shown in Figure 9. The variation in liver and kidneys DVHs for the two extreme phases was due to the change of the anatomy with respiratory motion. For liver and kidney, the 4D composite DVHs were around in the middle and showed the dosimetric reductions in the high dose region. The 4D composite DVH was derived from the summation over time and space through temporal deformable image registration. It reflected a dynamic dose distribution and assessed the dose delivered to each voxel of the region of interest during the organ motion.

Figure 8.

Dose volume histogram comparison of end-inhalation, end-exhalation phase plan, and the 4D plan for the PTV, cord, and lungs of patient.

Figure 9.

Dose volume histogram comparison of end-inhalation, end-exhalation phase plan, and the 4D plan for the PTV, liver, and kidney of patient.

Discussion

In principle, the accuracy of 4D plans lies in the accuracy of 4D image acquisition, the reproducibility of patient respiratory patterns, and the sorting process of respiratory signal to difference phases. Commercially available software provides the automatic ability to sort images retrospectively into the desired respiratory phases based on the temporal correlation between image data acquisition and the abdominal surface motion from the RPM system. The post-processing can produce phase errors and may introduce a phase shift. Rietzel et al. (23) reported that the RPM system inadequately models respiratory phase for about 30% of the patients at their institution due to the irregularities in the respiratory cycle. However, the phase shift itself does not degrade the 4D plan (17). The variations between the actual organ motion and acquired respiratory signal can degrade the accuracy of 4D delivery. Breathing training techniques had been proposed and may be helpful to retain the breathing regularity over the treatment course (24).

The residue uncertainty from the implementation of deformable registration needs to be taken into account for the 4D specific uncertainties as no single non-rigid image registration algorithm can be perfect for all anatomical situations. Various deformable registration algorithms have tradeoffs between the accuracy of organ deformation and the efficiency of computation. Currently, the most prevailing image registration algorithms available to the radiation oncology community include demons (25), free form deformation (26, 27), finite element modeling (28–30), thin-plate splines and B-splines (16, 31, 32), and diffeomorphic registration (17). An extensive and detailed comparison of different image registration methods is discussed in the literature (26, 33). Although the demons registration algorithm was used in our study, the inclusion of other methods to our software is very feasible and is the topic of ongoing research work from our group.

The study of automatic contour propagation is a complex matter and an active research topic. The method presented in this paper is based on the deformable registration of ROIs. Even though our patient study showed promise, more investigation needs to be carried out. Visual verification of the segmentation results is a necessary part of the validation process. Manual contour editing may be required if the automatic contour propagation is not satisfactory. Other methods such as elastically deform contour and surface model (34, 35) and automatic re-contouring using free from registration technique (36, 37) can achieve the same goal of automatic contour delineation in 4D planning. In this study, we chose a simple and straight-forward algorithm to implement the automatic contour propagation function to demonstrate the utility of the APT4D tool.

The next step after the computation of the 4D plan is the delivery of the plan. The 4D dynamic delivery for the conformal plan is a little easier than the IMRT plan due to the complexity of the IMRT plan itself. If the body motion is rigid and without deformation, the implementation is straight forward. The delivery of 4D radiotherapy is beyond the scope of this paper. Various factors need to be considered including the respiratory patterns prediction, the optimization of the leaf sequence, the leaf response, and limitations in acceleration and velocity, et cetera. Some pioneering works have been published (18, 38–40), but further developments and advancements are expected.

The efficiency in completing the 4D treatment plan is critical to its applicability. For the case that requires deformable image registration, the total time for the entire 4D planning on APT4D is about 15~20 minutes per phase depending on the size of the image matrix and the number of ROIs. This time does not include the time for the 3D plan in each phase and the time for manual delineation.

Conclusion

An integrated platform for 4D radiotherapy called APT4D has been developed for assisting the generation of a composite 4D treatment plan. The software platform includes an automatic non-rigid image registration, automatic contour mapping, and 4D dose combinations. A composite 4D treatment plan can be generated from the phase specific treatment plans that are summed using appropriately weighting factors. Preliminary results using the APT4D platform with deformable image registration showed that the software performs well in contour propagation as well as image and dose deformation. The automation and functionality added with APT4D have enabled us to improve the efficiency of the 4D treatment planning process.