Historical Divergence and Gene Flow in the Genus Zea

Abstract

Gene flow plays a fundamental role in plant evolutionary history, yet its role in population divergence—and ultimately speciation—remains poorly understood. We investigated gene flow and the modalities of divergence in the domesticate Zea mays ssp. mays and three wild Zea taxa using sequence polymorphism data from 26 nuclear loci. We described diversity across loci and assessed evidence for adaptive and purifying selection at nonsynonymous sites. For each of three divergence events in the history of these taxa, we used approximate Bayesian simulation to estimate population sizes and divergence times and explicitly compare among alternative models of divergence. Our estimates of divergence times are surprisingly consistent with previous data from other markers and suggest rapid diversification of lineages within Zea in the last ∼150,000 years. We found widespread evidence of historical gene flow, including evidence for divergence in the face of gene flow. We speculate that cultivated maize may serve as a bridge for gene flow among otherwise allopatric wild taxa.

GENE flow plays a fundamental role in plant evolutionary history, from maintaining cohesion among geographically separated populations (Morjan and Rieseberg, 2004; Arnold 2006) to accelerating evolution via adaptive introgression (Arnold 2004). Yet despite its importance, the role of gene flow in population divergence and speciation is poorly understood. Conventional theory argues strongly for the predominance of an allopatric model of divergence, in which populations are separated geographically and evolve in isolation without genetic exchange (Coyne and Orr 2004). Nonetheless, the simple allopatric model may not be appropriate for many plant lineages: ample plant data support the occurrence of population divergence (Antonovics 2006; Arnold 2006; Mallet 2007; Rieseberg and Willis 2007) and perhaps even speciation (Savolainen et al. 2006) in the face of gene flow.

While the population genetics of gene flow have been studied in numerous plant species (Hamrick and Godt 1989; Hamrick and Nason 1996; Coyne and Orr 2004; Morjan and Rieseberg 2004), few studies have made explicit attempts to study the process of population divergence. In fact, conventional analyses of gene flow often make assumptions about drift–migration equilibrium that preclude simultaneous evaluation of divergence and gene flow. Moreover, the vast majority of studies to date have not used DNA sequence data, instead relying on other molecular markers for which model-based inference is less tractable. Explicit molecular population genetic analysis of divergence between plant lineages has so far been limited to a handful of studies in Arabidopsis (Ramos-Onsins et al. 2004), rice (Zhang and Ge 2007), and tomatoes (Städler et al. 2005, 2008). These studies have advanced our understanding of divergence beyond a simple analysis of gene flow under equilibrium conditions, using coalescent methods to estimate divergence parameters and test the null model of divergence in isolation. But while all of these studies have suggested that their data provide evidence of introgression, none have been able to statistically reject a null model of isolation or draw firm conclusions about the role of gene flow in plant speciation.

The fact that no clear picture has emerged from these initial studies stems from several important limitations of the work to date. First, investigations have been limited to retrospective assessment of divergence between heterospecific populations, and such analyses may paint a different picture than studies of populations currently undergoing both divergence and gene flow. Second, studies to date have looked at only a handful (≤10) of loci, such that sampling variance may have as much effect as biological processes in determining observed patterns of variation. Third, and most importantly, these studies have all relied heavily on the divergence population genetic (DPG) approach of Hey and colleagues (Wakeley and Hey 1997; Wang et al. 1997), which uses coalescent simulations to test the fit of observed data to a model of divergence in isolation. While these approaches represent a substantial advancement, the goodness-of-fit test employed in these analyses is likely to be conservative for identifying introgression (Städler et al. 2008). More importantly, while newer software allows estimation of migration parameters (Hey and Nielsen 2004; Becquet and Przeworski 2007), the DPG approach and its descendants do not evaluate alternative models of divergence (but see Hey and Nielsen 2007 for an improved implementation).

Here we extend the DPG approach to investigate divergence and speciation in the genus Zea (Poaceae). The genus Zea is composed of four species distributed across Mexico and into Central America. Zea has historically been divided into two sections (Doebley and Iltis 1980; Iltis and Doebley 1980). Section Luxuriantes consists of the perennial Zea diploperennis, its autotetraploid derivative Z. perennis, and the annual Z. luxurians. The only species in section Zea is Z. mays, which is an annual composed of four subspecies: the domesticate maize (ssp. mays), its wild progenitor ssp. parviglumis, and the wild taxa ssp. mexicana and ssp. huehuetenangensis. A number of authors have utilized genetic data to elucidate relationships within Zea (Doebley et al. 1984; Buckler and Holtsford 1996; Hanson et al. 1996; Hilton and Gaut 1998; Tiffin and Gaut 2001; Fukunaga et al. 2005; Vigouroux et al. 2005), but substantial uncertainty remains about the evolutionary history of the genus, due in part to the complicating effects of hybridization and introgression (Wilkes 1977; Doebley 1990; Fukunaga et al. 2005). And while considerable attention has been directed toward maize domestication (Eyre-Walker et al. 1998; Hilton and Gaut 1998; Matsuoka et al. 2002; Tenaillon et al. 2004; Wright et al. 2005), the process of divergence among other lineages in Zea remains unclear. In particular, little is known about the role gene flow has played in diversification within Zea, even in the well-studied case of domestication.

In this study we combined existing sequence polymorphism data with new resequencing data to create a combined set of 26 loci sampled from Z. luxurians and three subspecies of Z. mays: ssp. mays, ssp. parviglumis, and ssp. mexicana (Figure 1). This sampling allowed us to study divergence at three distinct levels: recent domestication, subspecies differentiation, and speciation. We evaluated patterns of diversity in these four taxa, testing for evidence of recent introgression and investigating the history of selection using divergence data from the sister genus Tripsacum. We then utilized coalescent simulations under an approximate Bayesian framework to simulate four alternative models of divergence, explicitly evaluating the relative probability of our models and using the models to estimate effective population sizes and divergence times.

Figure 1.—

Geographical distribution of Zea luxurians and the wild subspecies of Z. mays. Circles represent collection locations from herbarium specimens in the Missouri Botanical Garden and approximate the geographic range of these taxa.

METHODS

Sampling:

We analyzed rangewide samples of Z. luxurians and three subspecies of Z. mays: the domesticate maize (ssp. mays), its wild progenitor ssp. parviglumis, and the wild ssp. mexicana. Basic passport information on the samples used can be found in supplemental Table S1, and geographic information about the wild taxa is presented in Figure 1.

DNA sequencing:

Sequencing methods followed Tenaillon et al. (2001, 2004). Amplified PCR products were cloned into a pGem TA cloning vector, and a single clone (single allele per individual) was then sequenced in both directions with BigDye chemistries on ABI automated sequencers. We reamplified and recloned individuals showing evidence of singleton polymorphisms in the initial alignment, sequencing five clones per individual per locus to confirm the sequence of the original allele. Singleton polymorphisms that could not be confirmed in this manner were assumed to be due to PCR error and were discarded from the analysis. We supplemented these data with sequence data from previous publications (supplemental Table S2) and with outgroup sequence from Tripsacum dactyloides at most loci. In total, we sampled sequence data from rangewide collections of an average of ∼13 individuals per taxon at 26 loci in four taxa of Zea (supplemental Table S2). All new sequences have been submitted to GenBank (accession nos. FJ707611–FJ708483).

Sequence analysis:

Sequences were initially aligned using the software Geneious (Biomatters) and then manually adjusted. Twelve of these loci were known genes, and previous determinations of exon structure were used for all analyses of these genes. For the remaining loci, we first identified open reading frames (ORFs) using a combination of the ORF-finding software at NCBI and in Geneious and using blastn searches of mRNA databases in GenBank. Final decisions on coding regions were based on assessment of the translation of potential regions and homology of the translated product with proteins found in GenBank. We calculated a suite of standard diversity statistics from nongapped, biallelic sites, including pairwise nucleotide diversity θ_π, Watterson's (1975) estimator θ_W, Tajima's (1989) D statistic, F_ST, and Hudson and Kaplan's (1985) Rmin, using the analysis package of software from the libsequence C++ library (Thornton 2003). We compared levels of silent diversity among taxa using the recursion equations of Hudson (1990) to estimate the multilocus value of θ (= 4Nμ, where N is population size and μ is mutation rate) for loci with samples from all four taxa. We estimated the likelihood of values of the population recombination rate ρ (= 4Nc, where c is the recombination rate per locus per generation) over a grid from 0 to 100, using the composite-likelihood approach of McVean et al. (2002) implemented in the software LDHat.

Detecting introgression:

We used the Bayesian clustering procedure of Pritchard et al. (2000) to test explicitly for recent introgression separately at each locus. We applied the program STRUCTURE (Pritchard et al. 2000) to data on the basis of two different genotype definitions. In the first, we defined haplotypes on the basis of sequence identity alone. In the second, we followed a procedure similar to Chen et al. (2009), dividing each sequence into regions following the four-gamete test algorithm of Hudson and Kaplan (1985). Haplotypes within each region were defined by sequence polymorphism, excluding regions with fewer than three polymorphic sites. Thus, the genotype of each individual at a locus was defined ultimately by its haplotype configuration across regions. With each of the two genotypic definitions, we tested for gene flow among all four taxa, using the software STRUCTURE (Pritchard et al. 2000) to estimate the assignment probability of each individual to its original population. We ran STRUCTURE under the no admixture model for haploid data for 200,000 steps, using predefined populations assumed to have correlated allele frequencies, and with a burn-in of 50,000 steps including 10,000 steps of admix burn-in. Following suggestions in the documentation, we tested for evidence of admixture up to two generations in the past, assuming a prior probability of migration of 1%.

Investigating selection:

We evaluated evidence for selection at these loci, using data on polymorphism and divergence from the 14 coding loci with samples from all four taxa and a Tripsacum outgroup (supplemental Table S2). As an initial test for selection, we performed the McDonald–Kreitman (MK) test (McDonald and Kreitman 1991) individually for all loci. We also performed the MK test on the pooled data, summing numbers of fixed and polymorphic synonymous and nonsynonymous sites across loci. For each taxon, we calculated the neutrality index (NI) (Rand and Kann 1996) as 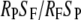, where R and S refer to counts of nonsynonymous and synonymous SNPs, and the P and F subscripts refer to polymorphic and fixed sites, respectively. An excess of fixed nonsynonymous sites relative to synonymous sites, often considered suggestive of positive selection, will lead to values of NI lower than unity, while an excess of polymorphic nonsynonymous sites may suggest purifying selection. Finally, we used counts of fixed and polymorphic sites to estimate the population selection parameter γ = 2Ns, where N is the effective population size and s is the selection coefficient. We estimated γ with the MKPRF software (Bustamante et al. 2002) for each locus separately as well as for data pooled across loci. We ran MKPRF with default parameters, except that burn-in and sampling were both extended to 5000 steps.

Approximate Bayesian computation:

We used an approximate Bayesian framework (Marjoram and Tavare 2006) to investigate four models of population divergence. For each model, we compared Z. mays ssp. parviglumis against three other taxa: Z. luxurians, Z. mays ssp. mexicana, and domesticated maize. All four models are variations of a simple divergence model (Wakeley and Hey 1997) in which an ancestral population instantaneously splits into two daughter populations of constant size (Figure 2). Our first model, referred to here as the isolation model, assumes no gene flow between populations. The second model is an island model with continuous gene flow between populations. In the sympatric model, gene flow occurs only during population divergence and is followed by eventual isolation between populations. Our fourth model, termed the allopatric model, posits initial population divergence in isolation followed by renewed contact and gene flow.

Figure 2.—

Schematic representation of the four divergence models tested for each comparison. See text for description of parameters. (A) Isolation. (B) Island. (C) Sympatry. (D) Allopatry.

All models incorporate the divergence time τ_D, scaled in units of 4N generations (N is the diploid effective population size), as well as the scaled population mutation rate θ and the population recombination rate ρ. Mutation and recombination parameters are defined for the reference population (θ₁, ρ₁, referring to Z. mays ssp. parviglumis in each case), the second daughter population (θ₂ and ρ₂), and the ancestral population (θ_A and ρ_A). Given the recent divergence between ssp. parviglumis and maize, we assumed θ_A = θ₁ for this comparison (Eyre-Walker et al. 1998; Wright et al. 2005). For models with gene flow, migration is included as the scaled parameter M = 4Nm (M₁ for migration into Z. mays ssp. parviglumis and M₂ for migration into population 2), where m is the per generation probability of a lineage having immigrated from outside of the current population. Gene flow begins at a time τ_A < τ_D for the allopatric model and ceases at time τ_S < τ_D in the sympatric model. To convert scaled parameter estimates to values in terms of years or effective population size, we used a mutation rate of 3 × 10⁻⁸/bp/year. This rate was estimated independently by Clark et al. (2005) from analysis of postdomestication mutations in locus tb1 and calibrated using archaeological data on the timing of maize domestication. This rate is higher than previous estimates based on less certain fossil evidence (Stebbins 1981; Gaut et al. 1996; White and Doebley 1999), but is nonetheless within the range of values thought plausible for plant nuclear sequences (Wolfe et al. 1987).

We simulated multilocus coalescent data under each of our models, drawing parameter values from specified prior distributions (supplemental Table S3). We used values of θ₁ and ρ₁ estimated from the data, and, assuming that c and μ do not vary among populations (but may vary among loci), placed uniform priors on the ratios θ_A/θ₁ and θ₂/θ_1. Identical uniform prior distributions were also used for the divergence times τ_D, τ_S, and τ_A, although the latter two parameters were constrained as described above. Finally, the prior distribution of the migration parameters M₁ and M₂ was also assumed to follow a uniform distribution, but independent values of M₁ and M₂ were drawn for each locus.

To estimate parameter values from these simulations, we used Bayes' theorem. Specifically, we can write 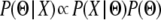, where Θ represents a vector of parameters of interest and X is the observed data. If the vector of summary statistics S is sufficient for the data, then . Given a proposed vector Θ, we can simulate the summary statistic vector S′; thus . To incorporate several continuously distributed summary statistics, we allow S′ to approximate S by including a tolerance parameter δ, such that ; with a uniform prior probability 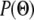this becomes , or the acceptance rate of simulations for a given vector .

For each simulated data set, we calculated the mean and variance across loci of four commonly used summary statistics (for a total of eight summary statistics): the number of shared (S_S) and fixed (S_F) silent sites between populations and the number of unique silent sites (S_X1 and S_X2) in each population (Wakeley and Hey 1997; Becquet and Przeworski 2007; Fagundes et al. 2007). These summary statistics were compared to observed summary statistics from our sequence alignments, rejecting simulations not within δ = 0.3 of both the mean and the variance of each statistic. Posterior distributions for the parameters of interest were then estimated as described above. Software used for the generation of priors, rejection sampling, and coalescent simulation is available from the authors.

RESULTS

Diversity and divergence:

We collected sequence data at 26 loci from an average of 13 individuals from each of four Zea taxa (supplemental Tables S1 and S2). Silent diversity varies greatly among these taxa (Table 1), with maximum-likelihood estimates of the population mutation rate θ in Z. mays ssp. parviglumis (hereafter simply “parviglumis”) and Z. mays ssp. mexicana (“mexicana”) significantly higher than estimates for Z. mays ssp. mays (“maize”) and Z. luxurians (“luxurians”) (Figure 3). Measures of nucleotide and haplotype diversity show a similar pattern (Table 1), pointing to a much larger effective population size in parviglumis and mexicana. Both of these taxa also contain an excess of low-frequency polymorphisms (high numbers of singletons and a negative Tajima's D). In contrast, maize and luxurians show a frequency spectrum shifted toward zero, with fewer singleton polymorphisms and Tajima's D values close to the expectation under neutral equilibrium. Differences in effective population size are reflected in our estimates of the population recombination rate ρ as well, with lower estimates for luxurians and maize (Table 1).

TABLE 1.

Diversity statistics at silent sites in the studied taxa of Zea

Taxon	S	η1	H	θπ	D	RM	ρ
Maize	20.9	6.8	0.802	0.013	0.002	2.1	0.032
parviglumis	25.7	13.4	0.936	0.017	−0.402	2.7	0.059
mexicana	24.4	12.1	0.906	0.016	−0.295	2.5	0.063
luxurians	11.3	5.1	0.807	0.010	−0.082	1.0	0.051

Shown are average numbers of segregating sites (S) and singletons (η₁), haplotype diversity (H), nucleotide diversity (θ_π), Tajima's D (D), Hudson and Kaplan's Rmin (RM), and the recombination rate per base pair (ρ).

Figure 3.—

Maximum-likelihood estimates of the population mutation rate θ in four taxa of Zea. Ninety-five percent C.I.'s can be approximated by the intersection of each curve with the horizontal shaded bar at −2.

Substantial variation is evident among loci (Table 2 and supplemental Tables S4–S6). Within parviglumis, for example, θ_π at silent sites ranges from 0.7% at locus gl1510 to 3.6% at d8 (Table 2). Loci also differ in frequency spectra, with Tajima's D values in parviglumis ranging from −1.68 at locus d8 to 1.55 at csu1138. The D value of several loci deviates significantly from the expectation of the standard neutral model, but only tb1 in maize remains significant after multiple-test correction (data not shown). In parviglumis, estimates of ρ per base pair are 0 for five loci (bnl7-13, c1, d8, csu636, and fus6), and as high as 0.48 for locus mgs3020 (Table 2).

TABLE 2.

Diversity statistics at silent sites for all loci in parviglumis

Locus	bp	n	S	η1	H	θπ	D	RM	ρ
adh1	808	8	57	27	0.964	0.026	−0.224	5	0.018
asg11	395	6	10	9	1.000	0.009	−1.069	0	0.001
asg35	467	12	31	19	0.985	0.016	−1.327	3	0.041
asg64	509	16	27	21	1.000	0.010	−1.505	1	0.058
asg65	531	14	20	4	0.912	0.013	0.297	2	0.005
bnl7-13	758	12	26	7	0.955	0.012	0.061	0	0.000
bz2	205	12	10	4	0.909	0.015	−0.255	1	0.037
c1	440	11	20	3	0.909	0.018	0.633	3	0.000
csu1132	330	8	28	16	0.964	0.029	−0.548	3	0.013
csu1138	186	14	5	1	0.835	0.012	1.547	1	0.047
csu1171	466	9	18	11	0.972	0.012	−0.869	1	0.010
csu381	916	10	42	24	1.000	0.014	−0.561	4	0.020
csu636	643	15	16	6	0.952	0.008	0.275	0	0.000
csu838	257	13	15	10	0.962	0.013	−1.186	2	0.120
d8	206	13	37	30	1.000	0.036	−1.677	2	0.000
fus6	153	10	4	2	0.644	0.010	0.143	0	0.000
gl1510	484	15	12	5	0.933	0.007	−0.437	2	0.137
glb1	511	8	52	37	1.000	0.033	−0.878	6	0.033
mgs3020	179	14	10	5	0.879	0.012	−1.254	2	0.483
pepc1070	712	13	63	22	1.000	0.029	0.098	8	0.016
pepc1150	233	16	15	8	0.883	0.015	−0.870	2	0.086
tb1	1982	7	79	49	0.952	0.015	−0.578	7	0.007
ts2	301	10	13	3	1.000	0.018	0.841	4	0.168
vp1010	167	12	9	4	0.803	0.017	−0.179	0	0.032
wip1	232	15	20	8	0.933	0.026	−0.088	4	0.060
wx1	497	19	29	14	0.994	0.013	−0.839	6	0.138

bp, number of silent sites; n, sample size; S, segregating sites; η₁, number of singletons; H, haplotype diversity; θ_π, nucleotide diversity per base pair; D, Tajima's D; RM, minimum number of recombination events; ρ, recombination rate per base pair.

We made an initial assessment of differentiation between taxa by calculating F_ST and counts of shared (S_S), fixed (S_F), and unique (S_X1 and S_X2) polymorphisms between pairs of taxa (Figure 4). F_ST clearly reveals a distinction between luxurians and Z. mays. Among the subspecies of Z. mays, parviglumis has the lowest median F_ST to luxurians, at 0.19. In contrast, the subspecies of Z. mays have substantially lower pairwise F_ST values. Among these taxa, parviglumis has lowest F_ST when compared to mexicana, perhaps suggesting large long-term population sizes in both taxa. Maize has a lower F_ST (0.066) with mexicana than with its wild ancestor, parviglumis (0.079). The distributions of S_S and S_F mirror the broad patterns revealed by F_ST (Figure 4). S_S is greater than zero in all pairwise comparisons among Zea taxa, but S_F > 0 between luxurians and all subspecies of Z. mays, suggesting some measure of isolation between species. Among the subspecies of Z. mays, only parviglumis and maize have a fixed difference between them, due to one SNP at locus asg65.

Figure 4.—

Divergence in Zea. (A) Distribution of pairwise F_ST values between Zea taxa studied. (B) Comparison of proportions of shared (S_S), fixed (S_F), and unique (S_X1 and S_X2) silent sites among pairwise comparisons. MA, maize; ME, mexicana; PA, parviglumis; LU, luxurians.

Selection:

If all mutations are neutral, drift alone should determine both the number of fixed differences between species and the level of polymorphism within species; the ratios of these values for different classes of SNPs are thus potentially informative about deviations from the expectation under neutrality (McDonald and Kreitman 1991). Using divergence information from a Tripsacum outgroup, we applied the MK test to the 14 loci with coding regions and with data representing each of our four Zea taxa (supplemental Table S2). None of the loci deviate significantly from neutral expectations in any taxon (data not shown). Consistent with the MK results, absolute values of the population selection parameter γ are low, with confidence intervals that overlap zero for most loci (Figure 5).

Figure 5.—

Estimates of γ = 2Ns, based on MKPRF analyses. Solid squares represent point estimates, with shaded bars showing the 95% C.I. of each estimate. A black vertical dashed line represents γ = 0 and gray dashed lines show the interval −1 < γ < 1. Loci adh1 and wx1 had too few sites in luxurians to estimate γ.

Analyses of individual loci may have low power to detect selection, and we thus analyzed samples pooled across loci. MK tests remain nonsignificant for counts pooled across loci, but the NI differs from unity for both parviglumis and maize (Table 3), suggesting deviation from neutrality in these taxa. For parviglumis, the NI of 0.76 differs from unity in a direction consistent with positive selection acting to fix nonsynonymous variants. For maize, an NI of 1.23 suggests the action of purifying selection preventing deleterious nonsynonymous variants from fixing. Estimates of γ from the pooled data are consistent with NI estimates; γ is estimated to be close to zero for mexicana and luxurians, but is slightly positive in parviglumis and slightly negative in maize (Table 3).

TABLE 3.

Inference of selection in Zea

Taxa	SNP type	Fixed	Poly	NI	γ
Maize	Synonymous	119	90	1.23	−0.30
	Nonsynonymous	58	54
mexicana	Synonymous	118	91	1.02	−0.06
	Nonsynonymous	61	48
luxurians	Synonymous	123	64	1.08	−0.10
	Nonsynonymous	64	36
parviglumis	Synonymous	108	135	0.76	0.33
	Nonsynonymous	62	59

Poly, polymorphic; NI, neutrality index.

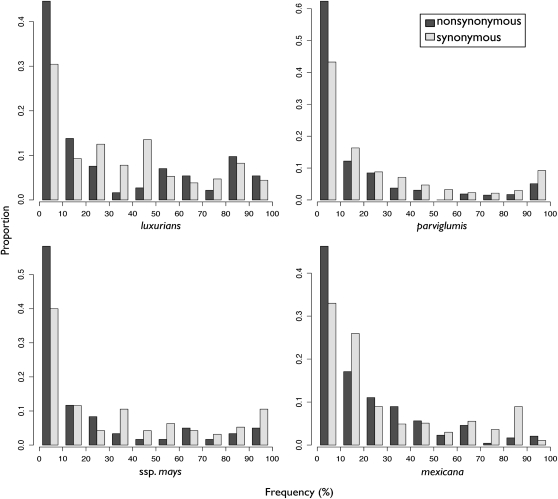
The comparison of polymorphic to fixed sites highlights long-term evolutionary patterns. To investigate more recent evidence of selection, we plotted the frequency spectrum of synonymous and nonsynonymous polymorphisms pooled across all 14 loci (Figure 6). All four taxa show an excess of low-frequency nonsynonymous variants, a pattern commonly taken to represent the effects of purifying selection preventing weakly deleterious mutations from rising to high frequency or fixing in a population (Fu and Li 1993).

Figure 6.—

Site frequency spectra of synonymous and nonsynonymous variants in each taxon. Frequency data have been binned into 10% intervals for plotting.

Evidence for introgression:

Low F_ST values and shared variants suggest the potential for gene flow among Zea taxa, but these measures do not allow explicit tests of migration. We more formally tested for the possibility of gene flow at each locus using the software STRUCTURE (Pritchard et al. 2000), comparing a null model of no admixture (in which individuals are assumed to be assigned to the correct population) to an alternative model of recent admixture in the past several generations. These analyses are motivated by the observation of shared sequences among taxa, including both entire sequences (supplemental Table S7) and sequence fragments. Using the entire sequence to define haplotypes, STRUCTURE analyses did not identify any likely cases of introgression (data not shown). Nonetheless, to examine the possibility that our observations of shared segments may be the result of past introgression events, we partitioned each locus into semi-independent fragments using the four-gamete test (see methods). Table 4 presents the results from these analyses, showing loci for which at least one genotype has a posterior probability of assignment to its original population of <50%. (cf. Fukunaga et al. 2005). Approximately half of the loci analyzed show evidence supporting introgression of sequence segments (Table 4). Most (∼70%) of these inferences point to recent introgression among subspecies of Z. mays, although there is a suggestion of gene flow between luxurians and one or more subspecies of Z. mays at six loci.

TABLE 4.

STRUCTURE analysis of putative admixture

	Taxon
Locus	Source	Destination
adh1	Maize	parviglumis
adh1	mexicana	parviglumis
adh1	parviglumis	Maize
adh1	Maize	mexicana
asg35	parviglumis	Maize
c1	Maize	parviglumis
csu1132	mexicana	luxurians
csu1132	luxurians	Maize
csu1132	parviglumis	Maize
csu1132	luxurians	mexicana
csu1132	Maize	mexicana
csu1132	Maize	parviglumis
csu1138	parviglumis	luxurians
csu1171	parviglumis	Maize
csu381	luxurians	Maize
csu381	mexicana	Maize
csu381	luxurians	mexicana
csu381	Maize	mexicana
csu381	Maize	parviglumis
csu838	mexicana	luxurians
pepc1070	parviglumis	Maize
pepc1070	parviglumis	mexicana
pepc1070	Maize	parviglumis
pepc1150	mexicana	Maize
pepc1150	parviglumis	mexicana
pepc1150	Maize	mexicana
tb1	mexicana	luxurians
tb1	Maize	mexicana
tb1	luxurians	mexicana
tb1	Maize	parviglumis
tb1	mexicana	parviglumis
wip1	mexicana	luxurians
wip1	parviglumis	Maize
wx1	mexicana	Maize

Each line represents a taxon pair/locus combination for which the posterior probability of assignment to the original taxon is <50% for at least one genotype.

Modeling population divergence:

STRUCTURE analyses suggest there may have been recent gene flow among taxa. To further examine the historical role of gene flow during divergence, we employed an approximate Bayesian framework to assess the probability of four alternative models of population splitting (Figure 2) in three independent divergence events. Our rejection-sampling scheme accepted simulated data that closely approximated the observed multilocus data. Using the acceptance rate P(S | Y₁), or the probability of the observed vector of summary statistics S given model Y₁, we calculated a Bayes factor representing the relative weight of the evidence for alternative model Y₁ over model Y₂, as . Following Jeffreys (1998), we considered values of K > 10^1/2 “substantial” evidence for model Y₁, thus rejecting model Y₂. Bayes factors comparing each of the four models to the isolation model are shown in Table 5. Evaluation of the four models for the parviglumis–luxurians divergence allows us to reject alternative models in favor of the sympatric model, suggesting a history of ancestral gene flow during divergence. For the parviglumis–mexicana comparison, models excluding recent gene flow (isolation and sympatry) exhibit notably lower probabilities, but only the isolation model can be rejected. The parviglumis–maize comparison reveals the opposite pattern: models including recent gene flow (island and allopatry) have the lowest probabilities, but only the island model can be rejected.

TABLE 5.

Relative probabilities of alternative divergence models

Comparison	Model	K
parviglumis–luxurians	Isolation	1.00
	Island	0.23
	Sympatry	3.27
	Allopatry	1.04
parviglumis–mexicana	Isolation	1.00
	Island	4.08
	Sympatry	1.50
	Allopatry	3.31
parviglumis–maize	Isolation	1.00
	Island	0.22
	Sympatry	1.17
	Allopatry	0.39

The Bayes factor (K) comparing each model to the isolation model is shown.

For each comparison, we performed parameter estimation under the most likely model by building a posterior density distribution of parameter values from accepted simulations (Figure 7). We took the highest probability value of each distribution as a point estimate of the parameter; using a recent estimate of the mutation rate in Zea (Clark et al. 2005), we converted parameter estimates into values of effective population size (N) and divergence time in years. While posterior probability distributions of the migration parameter M are not substantially different from our priors—suggesting that our data offer little power to quantitatively differentiate levels of gene flow among these taxa—distributions for all other parameters are clearly distinguishable. Estimates of effective population sizes reveal relatively similar values of N across the phylogeny: N's for mexicana, the parviglumis–mexicana ancestor, and the parviglumis–luxurians ancestor are all approximately the same as for modern-day parviglumis, or 120,000–160,000 individuals. The only estimates notably different from parviglumis are those of luxurians (θ₂/θ₁ ∼ 40% or 50,000 individuals) and maize (θ₂/θ₁ ∼ 30% or 45,000 individuals). Because our model restricts N to be constant within a lineage, however, these lower N values may represent strong population bottlenecks followed by recovery.

Figure 7.—

Parameter estimates of the most likely model for each of the three divergence comparisons to parviglumis. Posterior probability distributions are shaded and prior probability distributions are open. The mode of each parameter is given along with its conversion into N or years. Estimates are from the island model for parviglumis–mexicana and from the sympatric model for parviglumis–luxurians and parviglumis–maize (see Table 5).

The posterior distributions of τ_D all support divergence ≪4N generations (Figure 7), consistent with the observed levels of shared polymorphism (Figure 4). Our estimate of ∼55,000 years for the parviglumis–maize divergence is nearly indistinguishable from the mexicana divergence estimate of ∼60,000 years, but severalfold higher than current dates for the domestication of maize (Pohl et al. 2007); the estimated timing of isolation (τ_S) for parviglumis–maize is more recent (∼27,000 years), but still implausible given the archeological record. Divergence (τ_D) between parviglumis and luxurians is estimated at ∼140,000 years and followed by the cessation of gene flow (τ_A) at ∼60,000 years in the past.

DISCUSSION

Polymorphism and divergence:

We investigated diversity at 26 nuclear loci in four taxa of the genus Zea spanning three divergence events: between species, between subspecies, and between a domesticate and its progenitor. Even in the absence of coalescent models, our data provide information about the divergence history of the taxa studied. Given that the time to loss of shared variants is expected to be ∼2N generations (Clark 1997), the observed shared variation between luxurians and Z. mays (Figure 4) precludes an ancient divergence between these species without invoking either a very large effective population size for luxurians or a history of continual gene flow at all loci. Levels of recombination and diversity in luxurians (Table 1) attest to its reduced population size, however, and substantial unique polymorphism suggests that continual gene flow is unlikely. Among the subspecies of Z. mays, unique polymorphisms support the distinctness of mexicana and parviglumis, but patterns of shared variants and a low F_ST suggest a recent divergence and/or some amount of introgression (Figure 4).

The frequency spectrum of polymorphism provides information about changes in population size for these taxa. Negative values of Tajima's D are not expected from specieswide sampling except under population size expansion (see discussion in Arunyawat et al. 2007 and references therein). Along with previous evidence for population structure (Doebley et al. 1984; Fukunaga et al. 2005; Moeller et al. 2007), the observed negative D values in parviglumis and mexicana thus suggest a history of expansion, consistent with the fact that our coalescent estimate of N for the parviglumis–mexicana ancestor is roughly half that of the two descendant taxa combined. In contrast to mexicana and parviglumis, values of D near zero in maize and luxurians may reflect a reduction in effective population size. Multiple analyses of domestication have already suggested a population reduction for maize (Eyre-Walker et al. 1998; Hilton and Gaut 1998; Doebley 2004; Tenaillon et al. 2004; Wright et al. 2005); for luxurians, the suggestion of a population reduction is consistent with previous studies (Hilton and Gaut 1998), low diversity levels (Figure 3), low ρ-estimates (Table 1), and a restricted geographic distribution (Wilkes 1977; Doebley and Iltis 1980).

Selection:

Few striking patterns emerge from our analyses of selection. In luxurians, confidence intervals for all estimates of the population selection parameter γ overlap zero (Figure 5), consistent with estimates of a low effective population size from our divergence model. A low N decreases the efficacy of selection, allowing otherwise strongly deleterious variants to rise to appreciable frequencies before being removed from the population and converting weakly deleterious mutations into effectively neutral variants. The site frequency spectrum of luxurians hints at this possibility; only in luxurians are nonsynonymous polymorphisms more frequent than synonymous polymorphisms for both low-frequency categories (0–20%; Figure 6).

The evidence for selection in the three subspecies of Z. mays is more difficult to interpret. Given their extensive shared evolutionary history, one might expect strong correlations in the patterns of selection that compare divergence from Tripsacum to extant polymorphism. Superficially, shared history might seem to explain the striking correlation in estimates of γ between mexicana and maize (Pearson's r > 0.85; Figure 5), but the relatively distinct patterns of γ seen at loci in parviglumis (Pearson's r = 0.47 and 0.55 for comparisons with mexicana and maize, respectively) cast doubt on such an interpretation. A potential explanation for the relatively low correlation of γ between parviglumis and mexicana is that differences in population structure obscure shared history (e.g., Fukunaga et al. 2005). The striking correlation of γ between maize and mexicana could be indicative of recent gene flow (and thus shared history) between these taxa (Blancas et al. 2002; Baltazar et al. 2005; Fukunaga et al. 2005; Ellstrand et al. 2007); indeed, our analyses detect recent gene flow between maize and mexicana at several loci (Table 4).

Pooling data across loci, our results further suggest the possibility of adaptive evolution in parviglumis. The pooled estimate of γ for parviglumis is weakly positive and NI < 1 (Table 3); using the NI values as a crude estimate, as many as 25% of fixed nonsynonymous variants may have been subjected to positive selection. These results are far from conclusive, however, as the estimated value of γ is not significantly different from zero (Table 3) and we do not detect a negative correlation between nonsynonymous divergence and synonymous diversity (Pearson's r = −0.25, P = 0.39 after controlling for synonymous divergence), as might be expected from selective sweeps (Andolfatto 2007).

In plant lineages, similar estimates of selection are available only from the genus Arabidopsis. Initial investigation found evidence of negative selection in Arabidopsis thaliana, a result that was interpreted as consistent with the species' largely self-pollinating mating system (Bustamante et al. 2002). More recent work, however, has found similar patterns in both A. thaliana and its outcrossing relative A. lyrata (Foxe et al. 2008), suggesting that mating system alone is unlikely sufficient to explain differences in estimates of selection. While our data suggest some potential differences in the action of selection among taxa, all four taxa share a similar mating system, and, unlike the predictions of Bustamante et al. (2002), the taxon with the lowest estimated effective population size (luxurians) does not exhibit the most negative estimates of γ.

Models of divergence:

In addition to providing estimates of diversity and recombination, our multilocus data and stratified sampling of taxa within Zea allow for model-based population genetic analysis of divergence. Like the most recent incarnations of the DPG approach (Hey and Nielsen 2004, 2007; Becquet and Przeworski 2007)—and in contrast to other current methodologies (e.g., Kuhner 2006)—our approximate Bayesian approach incorporates both migration and divergence under the isolation model. Unlike other DPG methods, however, our approach allows for both the inclusion of recombination and a framework in which to explicitly test alternative models of population divergence and speciation.

None of our models of divergence can be systematically rejected in all comparisons, and in fact each finds some measure of support (K > 1) in at least one of the divergence events compared (Table 5). Overall, our modeling provides strong support for the sympatric model of divergence for the split between parviglumis and luxurians, for recent gene flow between mexicana and parviglumis (76% of total probability in the allopatric and island models), and in favor of models devoid of recent introgression for maize and parviglumis (78% total probability in the isolation and sympatric models). Comparison of Bayes factors further hints that gene flow between mexicana and parviglumis may have been continuous throughout their divergence and that parviglumis and maize may have diverged in sympatry. These differences among comparisons suggest that the divergence process is heterogeneous among taxa in Zea.

Our Bayesian estimates of divergence time (Figure 7) match surprisingly well with estimates based on allozyme differentiation between parviglumis and luxurians (135,000 years) and between parviglumis and mexicana (61,000 years) (Hanson et al. 1996). Additionally, our estimates of both divergence time and effective population size are broadly similar to those from previous analyses using fewer loci (Hilton and Gaut 1998; White and Doebley 1999) after accounting for differences in the substitution rates assumed.

Interpretation of the difference between archaeological data (Pohl et al., 2007) and our estimate of the parviglumis–maize divergence is not as straightforward. One possible explanation is that widespread selection during domestication has caused our loci to appear more divergent than expected under neutrality. This seems unlikely, however, given the small percentage of the genome thought to be under direct selection during domestication (Wright et al. 2005) and the rapid breakdown of linkage disequilibrium in the maize genome (Remington et al. 2001). Furthermore, our data lack strong evidence for selection, and reanalysis of the sympatric model excluding loci thought to be important for domestication (tb1, c1, d8, and ts2) still provides an overestimate of the divergence time (∼35,000 years, data not shown). Alternatively, several other scenarios might explain the high proportion of unique variants seen in maize (Figure 4) and thus the high estimates of divergence time. Our sampling of parviglumis, for example, might not have included samples of the population most directly ancestral to domesticated maize, and either a history of population expansion or conscious efforts on the part of cultivators to preserve diversity might have maintained more polymorphism in maize than expected under our constant-size model. Finally, although microsatellite analysis clearly shows that parviglumis is the wild ancestor of maize (Matsuoka et al. 2002), our data highlight the similarities of mexicana and maize and the possibility of extensive gene flow between them (see below). Such gene flow may help to explain why the estimated timing of the parviglumis–maize divergence is indistinguishable from the timing of the parviglumis–mexicana divergence with our methods.

Introgression and its consequences:

Our ABC model comparisons are based on mean patterns of shared, fixed, and exclusive polymorphisms over the entire data set and thus cannot identify gene flow events at individual loci. Additionally, our pairwise modeling approach cannot identify gene flow between taxa that were not compared (e.g., mexicana–maize). To complement our modeling efforts, we used STRUCTURE to perform tests for recent gene flow at individual loci. Although a number of loci share identical sequences between one or more of the taxa studied (supplemental Table S7), the STRUCTURE analysis using haplotypes defined by complete sequence identity did not uncover any likely cases of introgression at any locus. This may not be surprising, however; this approach is undoubtedly conservative because the data were reduced to a measure of either complete sequence identity or sequence difference, with no recognition of similarity. Because some individuals shared identity along long regions of sequence, we applied an alternative approach, defining haplotypes within nonrecombining segments (Chen et al. 2009) to represent genotypes at individual loci. With this approach, STRUCTURE analysis identified several sequence segments that appear to suggest recent gene flow (Table 4).

These STRUCTURE results are not without caveats, however. Because each region within a locus was treated as an independent marker, much of the gene flow identified as recent by STRUCTURE could reflect older introgression events broken up by subsequent recombination or may even be the product of shared (but rare) ancestral polymorphism. Moreover, STRUCTURE treats each region as independent, and linkage among these regions could mislead the analyses. Finally, our inferences of historical and recent gene flow—based on ABC and STRUCTURE analyses, respectively—are not in perfect agreement. This is not entirely unexpected, however, because the approaches are fundamentally different. It is not difficult to imagine, for example, that the mean numbers of shared and fixed variants could be suggestive of continued gene flow even if few loci show distinct enough patterns to be identified by STRUCTURE. Similarly, ABC might identify an overall pattern of isolation, but a few individual loci might show patterns suggestive of recent introgression.

In spite of these caveats, inspection of individual alignments supports the plausibility of our inference of recent gene flow for at least some loci. Shared derived indels, identified by comparison to the outgroup Tripsacum but not included in haplotype assignment or clustering analyses, are present in several of the loci highlighted by our STRUCTURE analysis. One particularly striking example is the shared presence of a 131-bp MITE-like transposable element insertion in two alleles of locus tb1 in luxurians and the purportedly introgressed segment in mexicana.

Overall, both coalescent and clustering approaches thus provide evidence for gene flow among the taxa of Zea. How reasonable are these inferences? While there is little empirical data to support a given model of speciation, previous work investigating introgression and gene flow substantiates our inferences of recent introgression. For example, hybridization is known to occur at least sporadically between domesticated maize and parviglumis (Wilkes 1977), and, despite genetic incompatibility factors limiting unidirectional gene flow between maize and mexicana (Evans and Kermicle 2001), the two taxa readily hybridize (Baltazar et al. 2005; Ellstrand et al. 2007). Allozyme data further suggest that introgression between maize and mexicana may be common (Blancas et al. 2002), and some evidence suggests that introgression from mexicana may have contributed to maize domestication (Gallavotti et al. 2004). Finally, although our data support both historical (Table 5) and more recent (Table 4) gene flow between mexicana and parviglumis, we are not aware of field observations of hybridization between these taxa, and they are not currently found in sympatry. It is likely, however, that the historical distribution of these taxa was different from that observed today (Wilkes 1972), and our results are corroborated by microsatellite evidence of admixture between these taxa (Fukunaga et al. 2005).

Although we identify one possible recent introgression event between Z. luxurians and parviglumis (Table 4), strong support for the “sympatric model” (Table 5) suggests that gene flow between these taxa has been predominantly historical. This inference is consistent with current geographic patterns, because luxurians is isolated from known populations of either parviglumis or mexicana (Wilkes 1977; Sánchez González and Ruiz Corral 1997; Fukunaga et al. 2005). Several lines of evidence nonetheless suggest that our inferred historical introgression is not implausible. Recent collections have identified populations of luxurians in the Mexican state of Oaxaca (Cuevas 2006), not far from the range of mexicana. Furthermore, extant populations of a fourth subspecies of Z. mays, ssp. huehuetenangensis, are currently found in Western Guatemala, suggesting that the ancestral ranges of Z. mays and luxurians may have overlapped to some extent.

If introgression has played both an historical and a recent role in Zea, what are the implications for systematic inference? Clearly, nuclear sequence data from multiple unlinked loci are not ideal for phylogenetic reconstruction because, among other reasons, introgression can obscure historical relationships. Nonetheless, we can use such data to generate a distance estimate (Nei and Li 1979) that can be converted to divergence time given the rate of substitution. We took this approach to see what light our data could shed on the larger phylogeny of the genus Zea. To accomplish this, we made use of sequences of the diploid perennial taxon Z. diploperennis (hereafter diploperennis) from adh1, c1, wip1, and wx1 (Tiffin and Gaut 2001). Nei's net divergence values at these four loci between parviglumis and luxurians (0.0169) and parviglumis and diploperennis (0.0148) seem to suggest a more recent common ancestor between parviglumis and diploperennis. However, using three of these loci to compare mexicana to both luxurians and diploperennis reveals the opposite pattern, and both luxurians and diploperennis are closer to Z. mays than they are to each other (data not shown). These incongruous values echo the conflicting phylogenies found with ribosomal DNA (Buckler and Holtsford 1996) and other markers (Doebley et al. 1984, 1987; Fukunaga et al. 2005). The possibility of introgression from diploperennis (Fukunaga et al. 2005) or luxurians (Doebley et al. 1984; this article) complicates estimates of divergence times from these numbers (Teshima and Tajima 2002), but they agree well with our Bayesian inference and previous estimates from other markers.

Together, these and other estimates (Gaut and Clegg 1993; Hanson et al. 1996; Hilton and Gaut 1998) suggest that the various species of Zea may have arisen nearly contemporaneously—on the order of 100,000–300,000 years using the mutation rate of Clark et al. (2005). Similar divergence measures between our outgroup Tripsacum and parviglumis (Nei's divergence = 0.0637) or luxurians (0.0729) provide estimates of ∼1–1.2 million years as the upper limit on the age of the genus. Although this is older than the estimates of White and Doebley (1999) based on divergence at terminal ear 1 (∼0.5 million years using the mutation rate of Clark et al. 2005), it agrees well with the observation from ITS data that speciation in Zea is recent compared to its divergence from Tripsacum (Buckler and Holtsford 1996).

Our ABC analyses suggest that these systematic inferences are complicated by historical introgression, and the STRUCTURE analyses open the possibility that recent introgression events may also cloud systematic relationships. One intriguing possibility, which might serve to explain support for recent (but perhaps limited) introgression between all of our taxa (Table 4), is that domesticated maize may serve as a bridge for the flow of alleles among wild taxa. Cultivated maize is nearly ubiquitous in Mexico and Guatemala and can be found in close proximity to all of the wild taxa of Zea. Data presented here and elsewhere (Wilkes 1977; Doebley et al. 1984; Baltazar et al. 2005; Fukunaga et al. 2005; Ellstrand et al. 2007) suggest that maize exchanges genes with its wild relatives. Broader sampling of maize and its wild relatives will be required to definitively test this hypothesis, but the possibility that domesticated maize may have functioned as a genetic go-between for wild populations certainly has profound implications both for the maintenance in situ of teosinte diversity and for our understanding of the risks and consequences of transgene escape from cultivated maize.