TABLE 2.

The density function and the information gain function for select distributions

Distribution	Density function	Information gain	Expected information	Parameter
Normal		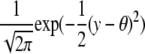y2		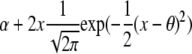θ
Cauchy		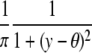		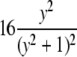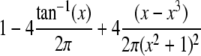θ
Logistic		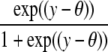		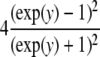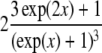θ
Exponential	(1/σ) exp(−y/σ), y > 0	4(y − 1)2	α + α log(α)2	θ = log(σ)
Gamma		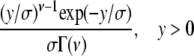4(y − ν)2		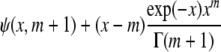θ = log(σ)
Weibull	(ν/σ) (y/σ)ν−1 exp(−(y/σ)ν), y > 0	4ν2(yν − 1)2	α + α log(α)2	θ = log(σ)

The parameter of interest for the first three distributions is the location parameter. For the last three, the parameter of interest is the scale parameter, the respective shape parameters being fixed. ψ(·, ·) is the incomplete Gamma function.