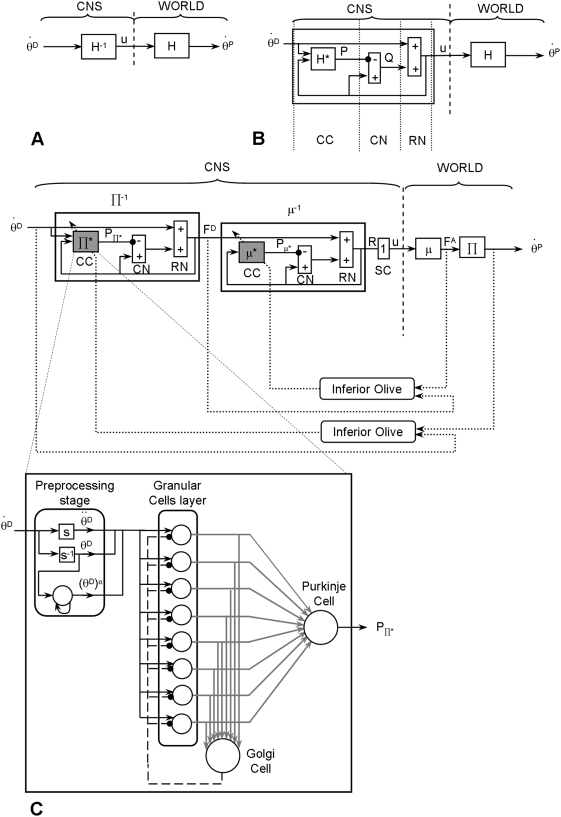
Figure 1. Main principles of the cerebellar architecture of the model.

For the sake of clarity, only the command circuit for one muscle is illustrated. (A) Structure of a command circuit accounting for the physical constraints. θ^D: desired movement; θ^P: performed movement; u: neural command. H: direct function incorporating all biophysical features of the limb. H⁻¹: internal inverse model of the direct function. (B) Control scheme used to compute an approximate inverse function. The two summing elements (positive/negative inputs) represent the cerebellar nuclei (CN) and the red nucleus (RN). H*: internal forward model of the direct function H. P and Q represent the signals originating from the cerebellar cortex (CC) and CN, respectively. (C) Direct functions Π* (representing the mechanical constraints, e.g. gravity, inertia) and μ (representing the muscle features) in the external world, and their counterparts in the CNS labeled Π* and μ*. These two internal forward models (Π* and μ*) are embedded through two internal feedback loops placed in series to calculate their approximate inverse, i.e., Π⁻¹and μ⁻¹. The direct pathways convey signals of desired position θ^D and forces F^D. In the indirect pathways, the negative output of the elements computing Π* and μ* are comparable to the inhibitory projections of the Purkinje cells of the cerebellar cortex to the neurones of the cerebellar nuclei. The P signals are comparable to simple spike activities of Purkinje cells. Dashed lines represent the climbing fibers. SC: spinal cord. Lower scheme: artificial neural networks simulating the CC. Granular, Golgi and Purkinje cells (respectively 8, 1 and 1 for each predictor) are modelled by formal neurones. s and s⁻¹ represent respectively the derivative and integration in the Laplace domain. α represents multiplicative higher orders of the position. The adaptive elements and connections are represented in grey, fixed elements in black. For the sake of the clarity only the first neural network is represented.