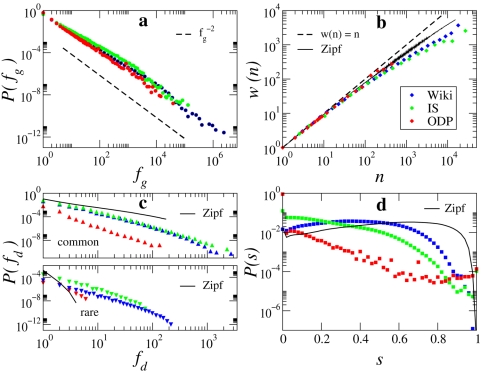
Figure 1. Regularities in textual data as observed in our three empirical datasets.

(a) Zipf's Law: word counts are globally distributed according to a power law 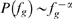. The maximum likelihood estimates of the characteristic exponent are 1.83 for Wikipedia, 1.78 for IS, and 1.88 for ODP. A Kolmogorov-Smirnov goodness-of-fit test [32] comparing the original data against 2500 synthetic datasets gives p-values for the maximum likelihood fits of 1 for Wikipedia and IS and 0.56 for ODP, all well above a conservative threshold of 0.1. This ensures that the power-law distribution is a plausible and indeed very good model candidate for the real distributions. (b) Heaps' law: as the number of words n in a document grows, the average vocabulary size (i.e. the number of distinct words) w(n) grows sublinearly with n. (c) Burstiness: fraction of documents P(f_d) containing f_d occurrences of common or rare terms. For each dataset, we label as “common” those terms that account for 71% of total word occurrences in the collection, while rare terms account for 8%. (d) Similarity: distribution of cosine similarity s across all pairs of documents, each represented as a term frequency vector. Also shown are w(n), the distributions of f_d, and the distribution of s according to the Zipf null model (see text) corresponding to the IS dataset.