EFFECTS OF TENSION-COMPRESSION NONLINEARITY ON SOLUTE TRANSPORT IN CHARGED HYDRATED FIBROUS TISSUES UNDER DYNAMIC UNCONFINED COMRESSION

Abstract

Cartilage is a charged hydrated fibrous tissue exhibiting a high degree of tension-compression nonlinearity (i.e., tissue anisotropy). The effect of tension-compression nonlinearity on solute transport has not been investigated in cartilaginous tissue under dynamic loading conditions. In this study, a new model was developed based on the mechano-electrochemical mixture model [Yao and Gu, J. Biomech. Model Mechanobiol. 2006; Lai et al., J. Biomech. Eng. 113:245-258, 1991] and conewise linear elasticity model [Soltz and Ateshian, J. Biomech. Eng. 122:576-86, 2000; Curnier et al., J. Elasticity 37:1-38, 1995]. The solute desorption in cartilage under unconfined dynamic compression was investigated numerically using this new model. Analyses and results demonstrated that a high degree of tissue tension-compression nonlinearity could enhance the transport of large solutes considerably in the cartilage sample under dynamic unconfined compression whereas it had little effect on the transport of small solutes (at 5% dynamic strain level). The loading-induced convection is an important mechanism for enhancing the transport of large solutes in the cartilage sample with tension-compression nonlinearity. The dynamic compression also promoted diffusion of large solutes in both tissues with and without tension-compression nonlinearity. These findings provide a new insight into the mechanisms of solute transport in hydrated, fibrous soft tissues.

INTRODUCTION

The main function of cartilaginous connective tissues such as articular cartilage and intervertebral disc is to transmit large loads during body motion. The mechanism which enables such soft hydrated fibrous tissues to support high loads is interstitial fluid pressurization. When the tissue sustains loads, the pressurization of interstitial fluid results from drag force acting on the interstitial fluid which is flowing through the dense extracellular matrix within the tissue [1,2]. The cells residing in the tissue continuously maintain the integrity of extracellular matrix so that the tissue can perform this remarkable mechanical function through decades. Due to the avascular nature of cartilaginous connective tissues, poor nutrition supply (e.g., oxygen and glucose) and insufficient removal of metabolic waste (e.g., lactate) are believed to be detrimental to viability and matrix synthesis of cells [3-8], leading to tissue degeneration [9]. Therefore, proper knowledge of solute transport mechanisms can lead to a better understanding of the nutrition-related etiology of cartilage degeneration.

Diffusion is believed to be a primary mechanism of solute transport in cartilaginous connective tissues and has been extensively studied [10-18]. The diffusion coefficients of solutes in articular cartilage decrease with increasing compressive strain on tissue [14-15,18]. The transport of solutes in articular cartilage can also be enhanced by convection which results from cyclic compression [19-21] or electro-osmosis [22]. It has been shown experimentally that dynamic compression augments the transport of large solutes in articular cartilage [15,19,20,23,24] but has little effect on the transport of small solutes [19,24]. Theoretical studies have also been conducted to investigate the mechanism of solute transport in cartilaginous tissues and gel under dynamic compression [25-27]. Mauck et al. [25] employed the mixture theory [1,28-30] to model the solute transport in uncharged hydrogel. The authors reported that the effects of dynamic loading on solute transport in the tissue were governed by several non-dimensional parameters and that the transport of large solutes could be enhanced under physiological loading condition. Yao and Gu [26] analyzed the transport of solutes in articular cartilage using the mechano-electrochemical mixture theory [29,30] and demonstrated that dynamic loading induced different responses [26] of solute flux for large and small solutes and the convective flows were affected by the fixed charge density.

The extracellular matrix of cartilaginous tissues often exhibits tension-compression nonlinearity. The tensile modulus of articular cartilage differs by two orders of magnitude from the compressive aggregate modulus, demonstrating a high degree of tension-compression nonlinearity [31]. More recently, theoretical models incorporating the tension-compression nonlinearity [32-36] have shown that interstitial fluid pressurization is considerably enhanced in compression by the disparity in tensile and compressive moduli of articular cartilage. The transport of solutes may be affected by this property as well. However, the effect of tension-compression nonlinearity on solute transport in cartilaginous tissues has not been studied. To precisely analyze solute transport in cartilaginous tissues under various loading conditions, the tension-compression nonlinearity of the extracellular matrix is incorporated into the mechano-electrochemical mixture model [29,30] in this study. The objective of this study was to examine the effects of dynamic loading on solute transport (diffusion and convection) in the cartilage samples with different degrees of tension-compression nonlinearity using this new theoretical formulation.

THEORY

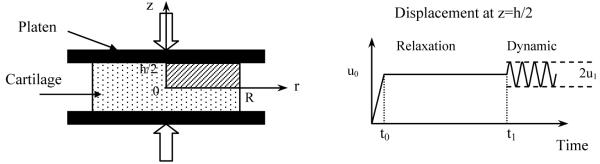
The framework of mechano-electrochemical mixture theories has been developed for cartilaginous tissues [29,30]. In the present study, desorption of neutral solute from cartilage explant under unconfined dynamic compression is of interest and numerically investigated (Figure 1). The size of the tissue explant is 1.5 mm in radius, R, and 1 mm in thickness, h (disk). The tissue is compressed between two rigid, frictionless, and impermeable loading platens. Initially, the tissue is equilibrated with a bathing solution of NaCl (c*=0.15M) plus an uncharged solute (concentration c^o* =40 nM). The strain components of the tissue at this initial state (relative to hypertonic configuration) are $E_{\mathit{rr}}^0$ (radial) and $E_{\mathit{zz}}^0$ (axial), and tissue dilatation is e₀($=E_{\mathit{rr}}^0+E_{\mathit{zz}}^0$). The osmotic pressure within the tissue is

$$p_o=\mathit{RT}[\Phi (c_o^{+}+c_o^{-})-2{\Phi }^{\ast }{c}^{\ast }+(\kappa \Phi -{\Phi }^{\ast })c^{o\ast }]-B_w{e}_o,$$ (1)

where R is the universal gas constant, T is the absolute temperature, $c_o^{+}$ is the initial concentration of Na+ and $c_o^{-}$ is the initial concentration of Cl⁻ within the tissue, Φ is the osmotic coefficient in tissue, Φ* is the osmotic coefficient in water, κ is the partition coefficient of uncharged solute, and B_w is the coupling coefficient [29]. It should be noted that the osmotic pressure depends on the value of tissue fixed charge density since the sum of $c_o^{+}$ and $c_o^{-}$ is a function of fixed charge density (due to electroneutrality condition). The concentration of uncharged solute in the tissue (c^o) is related to its concentration in the bathing solution (c^o *) by c^o = κ c^o *.

Figure 1.

Schematic of dynamic unconfined compression test configuration for solute desorption experiment. A ramp compression (u₀= 20% offset strain) was applied in 100s. After stress relaxation for 800,000s, a dynamic compression (u₁=2.5% or 5% dynamic strain) was imposed and the concentration of uncharged solute in the bathing solute was changed to zero.

At t=0, an offset compressive displacement −u₀ is applied on the tissue sample at a constant rate (=u₀/t₀) and is kept constant until the tissue reaches equilibrium at t=t₁. Then the tissue surface (z=h/2) is subjected to a sinusoidal displacement with amplitude of u₁ (Figure 1) and frequency of f, given as follows:

$$\mathrm{At}z=h∕2:u_z=\{\begin{array}{cc}u\left(t\right)=-u_{o}t∕t_o\text{when}\mathrm{t}<{\mathrm{t}}_0\hfill & \hfill \\ u\left(t\right)=-u_o\text{when}{\mathrm{t}}_0\le \mathrm{t}<{\mathrm{t}}_1\hfill & \hfill \\ u\left(t\right)=-u_o-u_1\sin \left[2\pi f(t-t_1)\right]\cdot H(t-t_1)\text{when}\mathrm{t}\ge t_1\hfill & \hfill \end{array}\phantom{\}}.$$ (2)

The initial and boundary conditions of the problem under consideration are similar to our previous study [37]. In the previous study, the solid matrix was assumed to be isotropic with equal mechanical behavior in tension and compression. A transport theory for charged hydrated soft tissue was developed based on the mechano-electrochemical mixture theory [37]. An isotropic, linear elastic constitutive law was used for the solid stress [37]. In the present study, the model is extended to account for tension-compressive nonlinearity of solid phase.

The total stress of a tissue is given by [26,37]

$$\sigma =-p\mathbf{I}+{\sigma }^s,$$ (3)

where p = RTε^w + RTΦ(c⁺ + c⁻ + c^o) − B_wtr(E) − p_o is the interstitial fluid pressure, ε^w is the modified chemical potential of interstitial water [38], c⁺ is the concentration of Na⁺, c⁻ is the concentration of Cl⁻, c^o is the concentration of neutral solute, p_o is the osmotic pressure at reference state, I is the identity tensor, tr(E) is the trace (i.e., dilatation) of infinitesimal strain tensor E (relative to load-free configuration, i.e., initial state in Eq. 1), and σ^s is the effective stress resulting from the deformation of the solid matrix. To account for the tension-compression nonlinearity of the solid matrix in cartilage, the Conewise Linear Elasticity (CLE) model of Curnier et al. [39] was used to model σ^s in Eq. (3). With the assumption of cubic material symmetry, the constitutive relation of stress and strain can be described as [34,35,40]

$${\sigma }^s\left(\mathbf{E}\right)=\underset{a=1}{\overset{3}{\Sigma }}\left\{{\lambda }_1\left[{\mathbf{A}}_a:\mathbf{E}\right]\mathit{tr}\left({\mathbf{A}}_a\mathbf{E}\right){\mathbf{A}}_a+{\lambda }_2\mathit{tr}\left({\mathbf{A}}_a\mathbf{E}\right)(\mathbf{I}-{\mathbf{A}}_a)\right\}+2\mu \mathbf{E}$$ (4)

where E = (Δu + Δu^T)/2 is the infinitesimal strain tensor related to the solid displacement u, A_a is the texture tensor corresponding to each of the three preferred material directions defined by the unit vector a_a with A_a = a_a ⊗ a_a (⊗ denoting the dyadic product of vectors), and λ₁, λ₂, and μ are the elastic constants. In this expression, the term ${\mathbf{A}}_a:\mathbf{E}=\mathit{tr}\left({\mathbf{A}}_a^T\mathbf{E}\right)$ represents the component of normal strain along the preferred direction a_a. The tension-compression nonlinearity stems from

$${\lambda }_1\left[{\mathbf{A}}_a:\mathbf{E}\right]=\{\begin{array}{cc}{\lambda }_{-1},\hfill & {\mathbf{A}}_a:\mathbf{E}+E_a^0<0\left(\text{compression}\right)\hfill \\ {\lambda }_{+-},\hfill & {\mathbf{A}}_a:\mathbf{E}+E_a^0>0\left(\text{tension}\right)\hfill \end{array}\phantom{\}}$$ (5)

where $E_a^0$ is the normal strain at the initial state along the direction a_a. Equation (5) indicates that λ₁ differs whether the normal strain component along the direction a_a is compressive or tensile. The physical meanings of the elastic constants are as follows: H_−A = λ₋₁+2μ and H_+A = λ₊₁+2μ are the equilibrium moduli of the tissue in confined compression and tension, respectively, λ₂ is the equilibrium ratio of radial stress to axial strain in confined compression, and μ is the shear modulus. The CLE model can be used to describe the isotropic stress-strain relation without tension-compression nonlinearity if λ₊₁= λ₋₁= λ₂.

The initial swelling strain of the cylindrical cartilage sample in axial ($E_{\mathit{zz}}^0$) and radial $E_{\mathit{rr}}^0$ directions due to the osmotic pressure can be determined using the following relation [40]:

$$E_{\mathit{rr}}^0=E_{\mathit{zz}}^0\approx \frac{p_0}{(H_{+A}+\Pi )+2({\lambda }_2+\Pi )},$$ (6)

where $\Pi =\frac{\mathit{RT}\varphi c_0^{F^2}}{{\varphi }_0^w\sqrt{c_0^{F^2}+4\frac{{\epsilon }^{-}{\epsilon }^{+}}{{\gamma }_{+}^{\ast }{\gamma }_{-}^{\ast }}}},{\epsilon }^{+},{\epsilon }^{-},{\gamma }_{+}^{\ast }$, and ${\gamma }_{-}^{\ast }$ are the modified (electro)chemical potentials and activity coefficients of cation and anion, respectively. The initial swelling strain was taken into consideration in the determination of λ₁ in Eq. (5) in this study.

At t=t₁, the bathing solution is instantaneously changed to pure saline solution (i.e., c*=0.15M and c^o*=0). The uncharged solute starts to transport from the tissue to the bathing solution (desorption) while the dynamic compression is applied to the tissue. The flux (J^α) of solute α [α = + (Na+), − (Cl−) and 0 (uncharged solute)] is the sum of convection flux ($J_{\mathrm{C}}^{\alpha }$) and diffusion flux (${\mathbf{J}}_{\mathrm{D}}^{\alpha }$) [37]:

$${\mathbf{J}}^{\alpha }={\mathbf{J}}_{\mathrm{C}}^{\alpha }+{\mathbf{J}}_{\mathrm{D}}^{\alpha },$$ (7a)

$${\mathbf{J}}_{\mathrm{C}}^{\alpha }=H^{\alpha }{c}^{\alpha }{\mathbf{J}}^w,$$ (7b)

$${\mathbf{J}}^w=-\mathit{RTk}\left(\nabla {\epsilon }^w+\underset{\alpha =+,-,0}{\Sigma }{H}^{\alpha }\frac{c^{\alpha }}{{\epsilon }^{\alpha }}\nabla {\epsilon }^{\alpha }\right),$$ (7c)

$${\mathbf{J}}_{\mathrm{D}}^{\alpha }=-{\varphi }^w{c}^{\alpha }{D}^{\alpha }\nabla {\epsilon }^{\alpha }∕{\epsilon }^{\alpha }.$$ (7d)

In Eq. (7), H^α is the convection coefficient of solute α [37], D^α is the diffusion coefficient of solute α, k is the hydraulic permeability of tissue, and ε^α is the modified (electro)chemical potential of solute α (α =+,−,0) [38].

Note that the convection coefficient, diffusion coefficient, and hydraulic permeability are functions of drag coefficients (f_αβ) between α and β phases (or constituents) used in the mixture theory [29,30]. For example, it can be shown that the hydraulic permeability k is related to drag coefficients by

$$k=\frac{\stackrel{-}{k}}{1+{\displaystyle \underset{\alpha =+,-,0}{\Sigma }}(1-H^{\alpha })\frac{f_{w\alpha }}{f_{\mathit{ws}}}}=\frac{\stackrel{-}{k}}{1+{\displaystyle \underset{\alpha =+,-,0}{\Sigma }}{H}^{\alpha }\frac{f_{\alpha s}}{f_{\mathit{ws}}}}$$ (8)

where $\stackrel{-}{k}=\frac{{\left({\varphi }^w\right)}^2}{f_{\mathit{ws}}}$ is the intrinsic permeability defined by Lai et al. [41]. Note that k ≈ k̄ if f_ws >> f_αs or H^α ≈ 1 (i.e., f_αw >> f_αs) [36].

These coefficients depend on tissue structure and composition. Several constitutive relations of hydraulic permeability and solute diffusivity to tissue strain (or porosity) have been reported in the literature for cartilaginous tissues [e.g., 42-44]. In the present study, the following constitutive relation is used for hydraulic permeability [42]:

$$k=\frac{a}{\eta }{\left(\frac{{\varphi }^w}{1-{\varphi }^w}\right)}^n,$$ (9)

where η is the viscosity of water, and a and n are the parameters which depend on the structure and composition of the porous media. Note that Eq. (9) is a special case of the formulation proposed by Holmes and Mow [43]. The constitutive relation for solute diffusivity is estimated as [44]

$$\frac{D^{\alpha }}{D_0^{\alpha }}=\exp \left(-A{\left(\frac{r_s}{\sqrt{k\eta }}\right)}^B\right),$$ (10)

where $D_0^{\alpha }$ is the solute diffusivity in aqueous solution, r_s is the Stokes-Einstein (i.e., hydrodynamic) radius of solute α, and A and B are the material constants.

Since the tissue porosity (ϕ^w) is related to the tissue dilatation (e) and the porosity ${\varphi }_0^w$ at the reference configuration (i.e. at e= 0),

$${\varphi }^w=\frac{{\varphi }_o^w+e}{1+e},$$ (11)

the hydraulic permeability (Eq. 9) and solute diffusivity (Eq. 10) are strain-dependent as well.

Non-dimensionalization and Numerical method

The variables were non-dimensionalized for numerical calculation and data presentation. The non-dimensional quantities are defined by

$$\begin{array}{cc}\hfill & \widehat{r}=\frac{r}{h},\widehat{z}=\frac{z}{h},{\widehat{u}}^s=\frac{{\mathbf{u}}^s}{h},{\widehat{v}}^s=\frac{{\mathbf{v}}^s}{H_{-A}{k}_0∕h},\widehat{t}=\frac{t}{h^2∕H_{-A}{k}_0},\widehat{\sigma }=\frac{\sigma }{{\mathit{RTc}}^{\ast }},\hfill \\ \hfill & {\widehat{D}}^{+,-,\mathrm{o}}=\frac{D^{+,-,\mathrm{o}}}{H_{-A}{k}_0},{\widehat{c}}^{+,-}=\frac{c^{+,-}}{c^{\ast }},{\widehat{c}}^{\mathrm{o}}=\frac{c^{\mathrm{o}}}{c^{\mathrm{o}\ast }},{\widehat{\epsilon }}^{w,+,-}=\frac{{\epsilon }^{w,+,-}}{c^{\ast }},{\widehat{\epsilon }}^{\mathrm{o}}=\frac{{\epsilon }^{\mathrm{o}}}{c^{\mathrm{o}\ast }},\hfill \\ \hfill & {\widehat{J}}^w=\frac{{\mathbf{J}}^w}{H_{-A}{k}_0∕h},{\widehat{J}}^{+,-}=\frac{{\mathbf{J}}^{+,-}}{H_{-A}{k}_0{c}^{\ast }∕h},{\widehat{J}}^o=\frac{{\mathbf{J}}^o}{H_{-A}{k}_0{c}^{o\ast }∕h}\hfill \end{array}$$ (12)

where k₀ is the reference permeability and h is the height of the specimen.

The details of the theoretical model and the finite element method used for solving the unconfined compression problem have been reported in our previous study [37]. Briefly, because of geometrical symmetry, a mesh of 2300 second-order triangle Lagrange elements was used to model the upper quadrant of the sample. The convergence of the numerical model was examined by refining the mesh and tightening the tolerance. The numerical accuracy was examined against the results of 2D triphasic stress-relaxation problem reported in the previous study [45].

The parameters used in this study were described as follows: temperature, T=298K, concentration of NaCl bathing solution, c*=0.15 M, and initial neutral solute concentration, c^o *=40 nM, diffusivities of solutes in water $D_0^{+}=1.28\times {10}^{-9}{\mathrm{m}}^2∕\mathrm{s}$, $D_0^{-}=1.77\times {10}^{-9}{\mathrm{m}}^2∕\mathrm{s}$, $D_0^0=1.22\times {10}^{-10}{\mathrm{m}}^2∕\mathrm{s}$, initial water content ${\varphi }_0^w=0.8$, coupling coefficient B_w=0, and initial fixed charge density c^F₀=0.2mEq/ml [26,46]. Based on experimental studies on cartilage [34,36], the elastic constants were chosen as H_+A = 0.5-10 MPa, H_−A = 0.5 MPa, λ₂=0.1 MPa, and μ=0.2 MPa. Note that the tissue is isotropic when H_+A = H_−A (i.e., λ₊₁= λ₋₁= λ₂). The values of A=1.25 and B=0.681 were used in the constitutive equation of solute diffusivity, i.e., Eq. (10) based on the study of solute diffusivity in agarose gels [44]. The hydrodynamic radii of cation (Na⁺) and anion (Cl⁻) were 0.142nm and 0.197nm, respectively, which were determined based on the corresponding diffusivity value in the aqueous solution at 25°C using the Stokes-Einstein equation. The various radii of uncharged solutes varied in the range 0.2-5 nm and the partition coefficient κ of uncharged solute was assumed to be 0.1 which is similar to the value of IGF-1 in cartilage [26]. For the uncharged solute and ions, the activity coefficient and osmotic coefficient (Φ) were assumed to be unity. The convection coefficient (H^α) was assumed to be unity for the ions and uncharged solute except for the results in Figure 5. The values of η = 0.001 Ns/m², a=0.00339 nm² and n=3.24 were used in Eq.(9) [42]. A reference permeability k₀=5×10⁻¹⁶m⁴/Ns was used for non-dimensionalization. The parameters of compressive loading in Eq. (2) were given as: offset strain u₀ = 20%, strain rate u₀/t₀ = 0.2%/sec, equilibrium time t₁ = 800000 sec, frequency of sinusoidal strain f = 0.01 Hz, and the amplitude of sinusoidal strain u₁ = 0%-5%. The thickness and radius of the cartilage sample were h = 1 mm and R = 1.5 mm, respectively. Since the analytical solutions for the unconfined compression problem defined in this study were only dependent on the location along the radial direction, the data represented in the next section were determined for the cross section of z= 0.

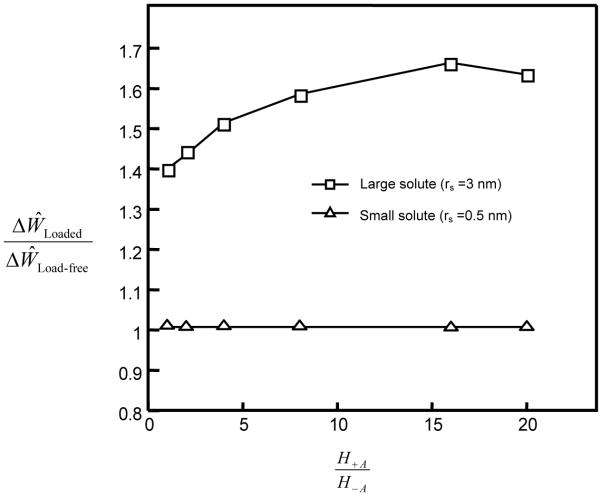
Figure 5.

Effects of convection coefficient and solute size on desorption in the samples with and without tension-compression nonlinearity. The loading conditions are the same as those described in Figure 3.

The change of total uncharged solute content in the tissue during dynamic loading (from t̂ = t̂₁ to t̂ = t̂₂) was evaluated as

$$\Delta \widehat{W}={\lfloor \int {\varphi }^w{\widehat{c}}^{\mathrm{o}}\cdot 2\pi \widehat{r}\widehat{h}d\widehat{r}\rfloor }_{\widehat{t}={\widehat{t}}_2}-{\lfloor \int {\varphi }^w{\widehat{c}}^{\mathrm{o}}\cdot 2\pi \widehat{r}\widehat{h}d\widehat{r}\rfloor }_{\widehat{t}={\widehat{t}}_1}.$$ (13)

The relative effect of dynamic loading on solute desorption was evaluated as the ratio of ΔŴ of loaded tissue to ΔŴ of load-free tissue $(\mathrm{i}.\mathrm{e}.,\frac{\Delta {\widehat{W}}_{\text{Loaded}}}{\Delta {\widehat{W}}_{\text{Load}-\text{free}}})$. Dynamic loading enhances solute transport if the ratio is greater than unity.

RESULTS

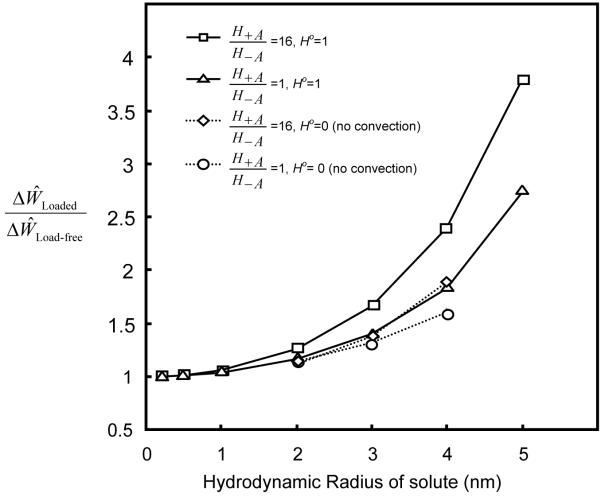
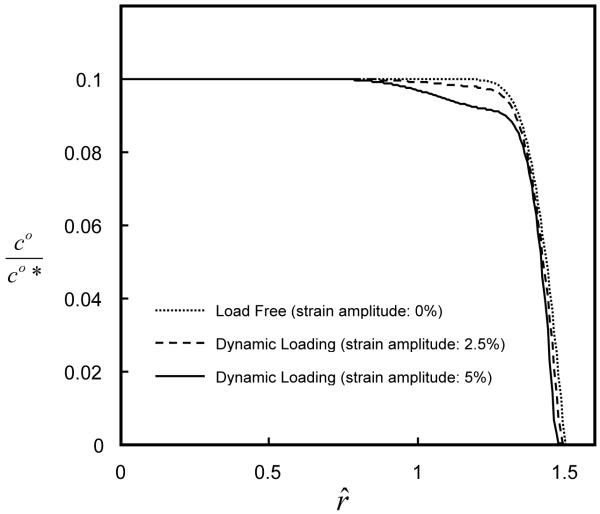
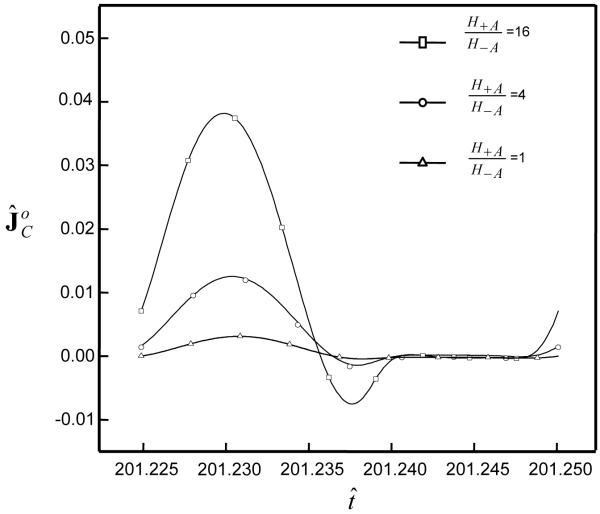
Dynamic loading enhanced solute desorption. The solute concentration (after 100 loading cycles) within the tissue decreased with increasing dynamic strain (f=0.01 Hz), see Figure 2. The ratio $\left(\frac{\Delta {\widehat{W}}_{\text{Loaded}}}{\Delta {\widehat{W}}_{\text{Load}-\text{free}}}\right)$ of amount of desorption in tissue with dynamic loading (5%) to that without dynamic loading increased with increasing ratio of H_+A / H_−A for a large solute (Figure 3). This is partially due to the fact that the solute convection increased with tension-compression nonlinearity. For example, at r̂ =1.45 during the 50^th loading cycle (f=0.01 Hz), the convective flux ${\mathbf{J}}_{\mathrm{C}}^0$ of a solute (r_s =3nm) increased with the ratio of H_+A / H_−A (i.e., increasing the degree of tension-compression nonlinearity), see Figure 4. Note that the convective flux of uncharged solute was zero at the tissue boundaries because of zero water flux at r̂ =0, ẑ =0 and ẑ =1 (due to geometrical symmetry and impermeable boundary) and zero concentration of uncharged solute at r̂ =1.5 , see Eq. (7b).

Figure 2.

Concentration distributions of uncharged solute (hydrodynamic radius: 3 nm) within the cartilage samples under two applied dynamic strains. In the simulations, the cartilage samples (H_+A / H_−A =16) were subjected to dynamic compressive loading with a frequency of 0.01 Hz and strain amplitude of either 2.5 or 5% for 100 cycles.

Figure 3.

Effect of tissue tension-compression nonlinearity on desorption of large and small uncharged solutes in tissues under dynamic compression. In the simulations, the cartilage samples were either load-free or subjected to dynamic loading with a frequency of 0.01 Hz and strain amplitude of 5% for 5000 sec (50 cycles). The amount of solute desorption (ΔŴ) was calculated for each of the two cases from t̂₁ =200 to t̂₂ =201.25, according to Eq. (13). The amount of desorption in a dynamic loading case was normalized by that in a load-free case.

Figure 4.

Profile of convective solute flux at the location r̂ =1.45 (ẑ =0) during the 50^th loading cycle. In the simulations, the cartilage samples (H_+A / H_−A =1, 4, and 16) were subjected to dynamic loading with a frequency of 0.01 Hz and strain amplitude of 5% for 50 cycles. The hydrodynamic radius of uncharged solute was 3 nm.

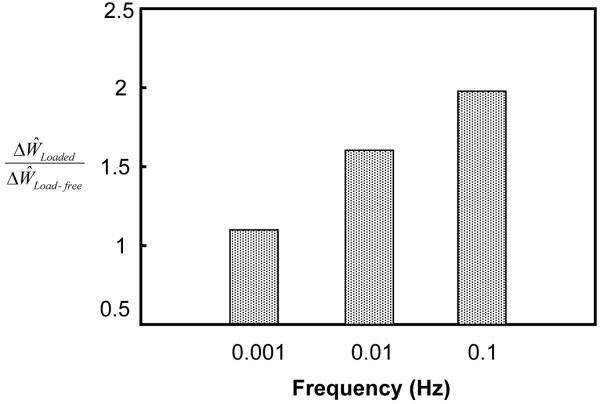
The ratio $\left(\frac{\Delta {\widehat{W}}_{\text{Loaded}}}{\Delta {\widehat{W}}_{\text{Load}-\text{free}}}\right)$ also increased with increasing solute size (Figure 5). If the convection effect was completely eliminated (by setting H⁰=0 in Eq. 7b) in the simulation, the ratio $\left(\frac{\Delta {\widehat{W}}_{\text{Loaded}}}{\Delta {\widehat{W}}_{\text{Load}-\text{free}}}\right)$ was reduced significantly for large solutes (2-4 nm) in the tissue with a high degree of nonlinearity (H_+A / H_−A =16). The ratio for the isotropic tissue (i.e., H_+A / H_−A =1), however, decreased slightly compared to the case of H⁰=1 (Figure 5). Note that the ratio was always greater than unity and increased with solute size, even though H⁰=0 (Figure 5). This indicates that dynamic loading (at 5% strain) also enhances solute diffusion when there is no convection effect (i.e., H⁰=0). The effect of dynamic loading on solute diffusion increased with solute size. In addition, the ratio $\left(\frac{\Delta {\widehat{W}}_{\text{Loaded}}}{\Delta {\widehat{W}}_{\text{Load}-\text{free}}}\right)$ increased with increasing loading frequency (Figure 6).

Figure 6.

Effects of loading frequency on solute desorption (hydrodynamic radius: 3 nm) in the samples with tension-compression nonlinearity (H_+A / H_−A =16). In the simulations, the cartilage samples were subjected to dynamic compressive loading with a frequency of either 0.1 Hz, 0.01 Hz, or 0.001 Hz and strain amplitude of 5% for 5000 sec.

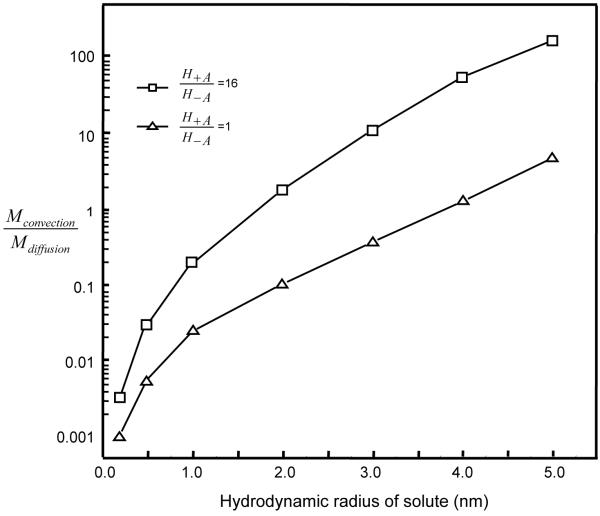
The amount of uncharged solute transported out of the subdomain between r̂ = 0 and r̂ = r̂_a by convectionor diffusion within a time interval (t̂ from t̂₁ to t̂₂) could be evaluated by: $M_{\mathit{convection}}{\int }_{{\widehat{t}}_1}^{{\widehat{t}}_2}{\mathbf{J}}_C^o{|}_{\widehat{r}={\widehat{r}}_a}\cdot 2\pi {\widehat{r}}_a\widehat{h}d\widehat{t}$ and $M_{\mathit{diffusion}}={\int }_{{\widehat{t}}_1}^{{\widehat{t}}_2}{\mathbf{J}}_D^o{|}_{\widehat{r}={\widehat{r}}_a}\cdot 2\pi {\widehat{r}}_a\widehat{h}d\widehat{t}$. The ratio of M_convection / M_diffusion is known as the Peclet (Pe) number. This ratio (or Pe number) was highly sensitive to solute size (Figure 7). For example, in the tissue with a high degree of nonlinearity (H_+A / H_−A =16, 5% dynamic compression for 50 cycles at f=0.01 Hz), the ratio (within the 50^th cycle) increased from 1.7 for r_s = 2nm to 150 for r_s = 5nm solutes at the location r̂ =1.45. The ratio was less than 1 for small solutes with hydrodynamic radius < 2 nm (Figure 7). The ratio was also sensitive to tissue nonlinearity. For the isotropic tissue (H_+A / H_−A =1) under the same loading condition, the ratio was less than 1 for solutes with radius up to 4 nm (Figure 7), indicating diffusion was a major mechanism for solute transport in the isotropic tissue.

Figure 7.

Ratio of the amount of uncharged solute removed by convection to that by diffusion in the subdomain between r̂ = 0 and r̂ = 1.45 during the 50^th loading cycle. The loading conditions are the same as those described in Figure 3.

DISCUSSION AND CONCLUSIONS

The objective of this study was to examine the effects of tissue tension-compression nonlinearity on solute transport in cartilage samples under dynamic unconfined compression. Articular cartilage exhibits a large disparity between tensile and compressive properties with the tensile modulus being about two orders of magnitude greater than the compressive modulus [31]. Under axial unconfined compression, the cylindrical cartilage sample is subjected to tension in the radial and circumferential directions. Due to its tension-compression nonlinearity, the tissue sample behaves “anisotropically” in the unconfined compression mode. The strains in the radial and circumferential directions are smaller (due to higher tensile modulus in these directions) compared to that in the axial direction, resulting in a larger volume change (i.e., dilatation) compared to an isotropic tissue (i.e., without tension-compression nonlinearity). Thus, the same dynamic load in the axial direction will cause higher water flux (relative to solid) in the radial direction in the tissue with tension-compression nonlinearity. This is consistent with our finding that the loading-induced enhancement of solute transport depends on the degree of tension-compression nonlinearity. Dynamic loading induces a higher convective solute flux in the cartilage sample with a higher degree of tension-compression nonlinearity (Figure 4), resulting in a larger enhancement in the transport of large solutes (Figures 3 and 5). The effects of convective flux on solute transport have also been examined by adjusting the convection coefficient H^α in Eq. (7b). After completely eliminating the effects of convection by substituting H^o =0 for the uncharged solutes in the simulations, the results showed that loading-induced enhancement of solute transport in the cartilage sample with a high degree of tension-compression nonlinearity solute transport in the cartilage sample with a high degree of tension-compression nonlinearity (H_+A / H_−A = 16) reduced much more than that in the isotropic sample (H_+A / H_−A = 1) (Figure 5). This indicates that convection is an important mechanism for enhancing the transport of large solutes in the cartilage sample with tension-compression nonlinearity by dynamic compression. However, the transport of large solutes is also enhanced by dynamic loading in both cartilage samples with and without tension-compression nonlinearity after eliminating convection effects. This indicates that diffusion of large solutes is also promoted by dynamic loading.

The relative importance of convection over diffusion (i.e., Pe number) depends on both solute size and tension-compression nonlinearity. Under dynamic unconfined compression (5% dynamic strain at f=0.01 Hz), convection is an important mechanism of transport for large solutes (r_s > 2 nm) in the tissues with high degree of tension-compression nonlinearity while diffusion is the major mechanism of transport for both small and large solutes (r_s < 4 nm) in the isotropic tissue (Figure 7). This is consistent with the previous studies [15-25] and our recent study on solute transport in isotropic cartilage tissues [37]. However, caution should be exercised when the ratio of convective flux to diffusive flux (i.e., Pe number) is used for interpreting the mechanism of solute transport. For example, at tissue boundaries, the convective flux of uncharged solute is always zero in this desorption experiment (due to boundary conditions of either relative water flux being zero or the concentration of uncharged solute being zero). The absence of convective flux at the boundary does not necessarily mean there is no convection effect within the tissue.

Note that the results in Figure 7 are based on the assumption that the convection coefficient for uncharged solute is unity (i.e., H⁰ = 1, in Eq. 7b). Recently, an experimental study showed that H⁰ < 1 for large solutes in articular cartilage [20]. Our theoretical study showed that the range of H^α is $\frac{D^{\alpha }}{D_0^{\alpha }}\le H^{\alpha }\le 1$ [37]. If H^α is equal to the lower bond of that range, its value could be close to zero for large solutes based on Eq. (10) (e.g, $\frac{D^{\alpha }}{D_0^{\alpha }}=0.035$ for a solute with r_s = 3 nm). Thus, it is necessary to determine convection coefficient (H^α) in tissue in order to ascertain the effect of convection on solute transport.

The theoretical model used in this study was highly nonlinear and coupled [29,37]. It took into consideration tissue tension-compression nonlinearity and four strain-dependent properties (fixed charge density, hydraulic permeability, solute diffusivity, and volume fraction of water). Our results showed that while Pe number increases with solute size (Figure 7), the effect of dynamic loading on solute diffusion also increases with solute size (Figure 5). This is believed to be due to the nonlinear coupling effects among solute concentration, tissue deformation, and strain-dependent solute diffusivity. This finding is also consistent with our previous study on solute transport in the isotropic tissue under dynamic unconfined compression [37].

The analyses in the present study used more realistic material properties of a hydrated fibrous tissue thus provided more useful predictions on solute transport in cartilaginous tissues under dynamic compressive loading. However, the analyses in this study did not take all factors into consideration. For example, intrinsic viscoelasticity of the solid matrix (which can further increase the degree of tension-compression nonlinearity in articular cartilage under physiological loading [35,36]) may have an effect on solute transport in the tissue. Solute binding to the solid matrix is another factor affecting solute transport. Furthermore, the value of H^α and its constitutive relation need to be further investigated in order to precisely analyze the mechanism for solute transport.

In summary, our analyses and results in the present study have demonstrated that the high degree of tissue tension-compression nonlinearity could enhance the transport of large solutes considerably in the cartilage sample under dynamic unconfined compression, but has little effect on the transport of small solutes at 5% dynamic strain level. The loading-induced convection is an important mechanism for promoting the transport of large solutes in the cartilage sample with tension-compression nonlinearity. Furthermore, dynamic compression also enhances diffusion of large solutes in both samples with and without tension-compression nonlinearity when there is no convection effect. These findings suggest that tissue tension-compression nonlinearity may play an important role in the transport of large solutes (e.g., growth factors) within cartilaginous tissues under physiological loading. This study provides a new insight into the mechanisms of solute transport in hydrated, fibrous soft tissues under dynamic compression.