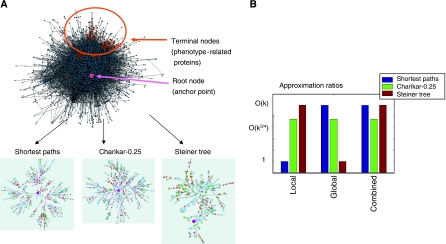
Figure 1.

Method overview. (A) Illustration of the network construction problem. We are given a network of interacting proteins, a subset of phenotype-related proteins (terminal nodes), and an anchor point (root node). The goal is to construct a subnetwork composed of signaling-regulatory pathways that lead from the phenotype-related set to the anchor point. We use three approaches for reconstructing these subnetworks––local optimization using the shortest path algorithm, global optimization using the Steiner tree algorithm and the intermediate approach using the Charikar-α algorithm. (B) Theoretical approximation bounds are displayed for the global, local and combined objectives. k is the number of terminal nodes. In this figure, we use an α value of 0.25. In the general case (0⩽α⩽0.5), Charikar-α provide bounds of O(k^1–α), O(k^½+α), and O(k^{max{1–α,½+α}}) for the global, local and combined objectives respectively (Supplementary information).