Abstract
It is becoming increasingly clear that the transfer of an electron across a protein-protein interface is coupled to the dynamics of conformational conversion between and within ensembles of interface conformations. ET reactions in conformationally mobile systems provide a ‘clock’ against which the rapidity of a dynamic process may be measured, and we here report a simple kinetic (master equation) model that self-consistently incorporates conformational dynamics into an electron transfer (ET) photocycle comprised of a photoinitiated ‘forward’ step and thermal return to ground. This kinetic/dynamic (KD) model assumes an ET complex exists as multiple interconverting conformations which partition into an ET-optimized (reactive; R) population and a less-reactive population (S). We take the members of each population to be equivalent by constraining them to have the same conformational energy, the same average rate constant for conversion to members of the other population, and the same rate constants for forward and back ET. This model successfully describes the changes in the ET photocycle within the ‘pre-docked’ mixed-metal hemoglobin (Hb) hybrid, [α(Zn), β(Fe3+N3-)], as conformational kinetics are modulated by variations in viscosity (η = 1-15 cP; 20 °C). The description reveals how the conformational ‘routes’ by which a hybrid progresses through a photocycle differ in different dynamic regimes. Even at η = 1 cP the populations are not in fast exchange and ET involves a complex interplay between conformational and ET processes; at intermediate viscosities the hybrid exhibits ‘differential dynamics’ in which the forward and back ET processes involve different initial ensembles of configurational substates; by η = 15 cP the slow-exchange limit is approached. Even at low viscosity the ET-coupled motions are fairly slow, with rate constants of < 103s-1. Current ideas about Hb function lead to the testable hypothesis that ET in the hybrid may be coupled to allosteric fluctuations of the two [α1, β2] dimers of Hb.
INTRODUCTION
The study of long-range electron transfer (ET) occupies a central place in modern biology and chemistry.1,2 However, it is becoming increasingly clear that the transfer of an electron across a protein-protein interface almost invariably is coupled to the dynamics of conformational conversion between and within ensembles of interface conformations.3-17 This is true for large multi-component redox systems that involve tightly-bound and precisely arranged redox centers, such as the [reaction center, cytochrome c2] complex,12 the [electron transferring flavoprotein, medium chain acyl-CoA dehydrogenase] complex,18 and the [plastocyanin, photosystem I] complex.19 Indeed, such systems often exhibit ET reactions that are gated3,6,8,9 – controlled by the dynamics rather than the ET process. Such coupling also occurs in simpler complexes of small, weakly-bound redox protein partners. In these cases, ET-active configurations are only rarely sampled during many diffusional encounters, and the complexes can exhibit conformational ‘phase space’ control by a process denoted dynamic docking.4,20,21 In response to the experimental investigations of these phenomena there have been numerous theoretical studies, with diverse approaches that range from diffusion-dynamics22,23 to kinetic/master-equation treatments.24
In the case of photoinitiated ET, both experimental and theoretical studies generally have focused on the photostimulated ‘forward’ ET process (rate constant kt) and infrequently10,25,26 considered an entire ET photocycle (Scheme 1) comprised of both forward and ‘back’ ET(rate constant kb). However, our recent work suggests that detailed studies of a full photocycle might give a more complete picture of the dynamics of a protein interface, in part at least because the forward and back ET processes should involve different initial ensembles of configurational substates (Fig 1).5,27 The forward ET reaction is initiated with the system in its equilibrium ensemble of configurations. When most – or the most stable – ensemble members exhibit low ET rate constants, then forward ET is controlled by conformational conversion to a reactive state. In contrast, because the photoinitiated ET process necessarily generates an ET intermediate that is in a reactive configuration, the back reaction begins in a non-equilibrium conformation and is controlled by the competition between direct back ET and deactivation from this conformation, Fig 1. Evidence for such ‘differential dynamics’ effects within a photocycle was obtained from examination of the effects of viscogens and interface mutations on the forward and back ET reactions of four ET complexes encompassing a wide range of energy landscapes and stabilities: the weakly-bound and highly dynamic [hemoglobin (Hb), cytochrome b5] and [myoglobin, cytochrome b5] complexes; the moderately bound [cytochrome c peroxidase, cytochrome c] complex; and the structurally defined, mixed-metal Hb hybrids, [α(Zn), β(Fe3+L)].5
Scheme 1.
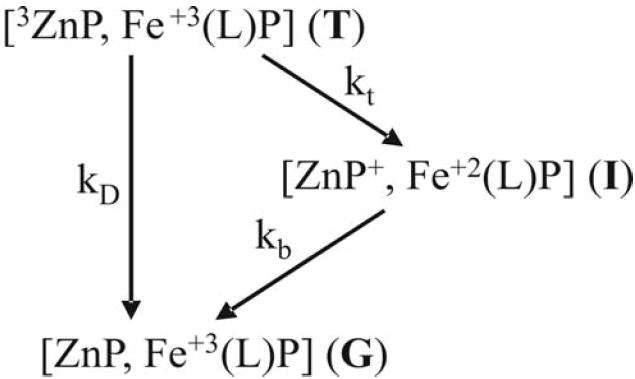
Figure 1.
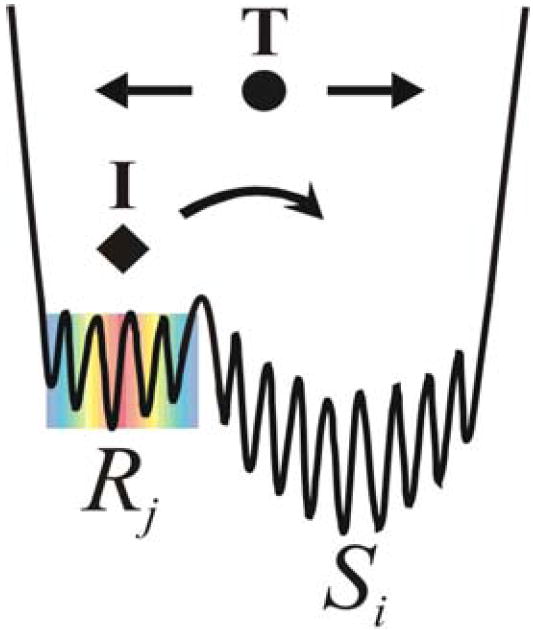
Cartoon of the ‘differential dynamics’ energy landscape for forward and back ET, with Rj reactive substates and Si less reactive substates. Dot (●) represents the system point for the equilibrium ensemble of configurations that exist at the start of a photo-initiated ET process and diamond (◆) represents the system point subsequent to forward ET and prior to return of ET intermediate to ground.
Mixed-metal Hb hybrids in particular provide an ideal system with which to explore dynamic control of an ET photocycle involving pre-docked protein redox partners.28-31 The hybrid is an [α(Zn)2, β(Fe)2] tetramer and ET occurs within two independent pairs of [α1(Zn), β2(Fe)] ET partners, across distances of about 17 Å between heme edges and 25 Å between metal ions, Fig 2.32-35 However even this ‘pre-docked’ tetramer can access multiple configurations, as shown by recent NMR36-38 and x-ray39-42 studies. Previous work revealed a coupling of ET to conformational conversion among these configurations through the failure of the simple kinetic equations for the photocycle of a rigid complex (Scheme 1) to describe the viscosity (η) dependence of the hybrid photocycle.5,27 Instead the forward and back ET steps exhibited ‘differential dynamics’; as the interfacial dynamics were slowed with increasing η the apparent forward ET rate constant decreased, whereas the apparent back ET rate constant increased.5,27
Figure 2.
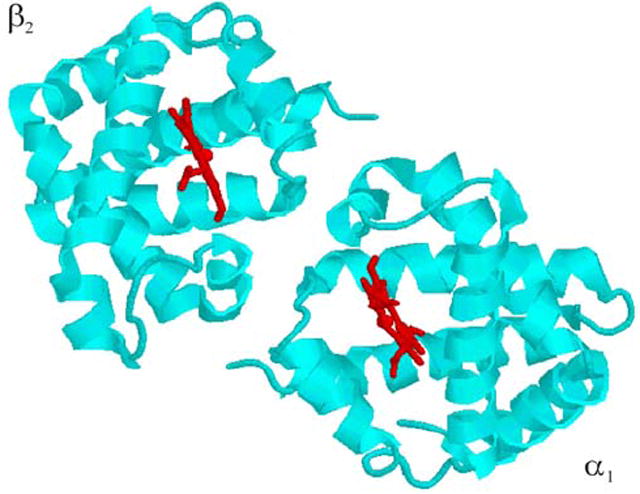
One [α1, β2] ET ‘complex’ of a T-structure hemoglobin tetramer; hemes shown in red.
Although this description in terms of viscosity-dependent ET rate constants provided qualitative insights into the coupling of the ET photocycle to conformational dynamics, the kinetic equations used did not explicitly include dynamic processes, and indeed did not represent any well-defined kinetic mechanism. Therefore we have developed, and herein describe, a simple kinetic (master equation) model that explicitly incorporates such processes into a photocycle. This ‘KD’ model has been applied to experiments in which we monitor the photocycle of a mixed-metal Hb hybrid as conformational kinetics are modulated by variations in viscosity at fixed temperature, thereby avoiding changes in the microscopic rate-constants that would come with variations in temperature. We find that the experiments are well-described with the KD model, and that there are conditions under which the behavior of the Hb hybrids in fact corresponds to the postulated differential dynamics paradigm for dynamically controlled ET that is sketched in Fig 1. The analysis further introduces the idea of a conformational ‘route’ by which a hybrid progresses from a photo-activated triplet state, through an ET intermediate, then back to ground, and reveals how these routes evolve as the system traverses through distinct dynamic regimes. The possible nature of the ET-coupled conformational motions are considered in light of current ideas about Hb function.43 Finally, the advantages offered by studying an ET photocycle are discussed and limitations of the KD model are examined.
EXPERIMENTAL PROCEDURES
Materials
Hemoglobin was acquired from outdated human erythrocytes obtained from Life Source (Skokie, IL). NaN3, K3Fe(CN)6, IHP (inositol hexaphosphate), and Sephadex G25 were obtained from Sigma-Aldrich. Glycerol, K2HPO4 and KH2PO4 were obtained from VWR and zinc protoporphyrin IX (ZnP) from Frontier Scientific. H2O was purified by a MilliQ water purification system (Millipore). Prepurified N2(g) from Air Gas was used for all deoxygenating operations.
Preparation of [α(Zn), β(Fe3+N3-)]
Hemoglobin was purified by anion exchange chromatography, and separated into its component chains as described previously.44,45 After removal of bound mercurial with mercaptoethanol, the heme was extracted from the α-chains and the apo-α-protein was reconstituted with ZnP and recombined with the native β-chains to give the [α(ZnP), β(FeCO)] hybrid as described earlier.44-46 The [α(ZnP), β(FeCO)] hybrid was oxidized at 4°C with a 5-fold excess of K3Fe(CN)6 at pH 6 with a N2 stream over the solution. Excess ferricyanide was removed and the hybrid hemoglobin converted to the azidomet form by passage over G-25 resin equilibrated with a phosphate-buffered solution containing 100 mM sodium azide at pH 7.
Cryosolutions of varying viscosity were prepared at selected compositions (w/w) of glycerol and deionized water. Stock solutions of 50 mM monobasic and dibasic phosphate were prepared by dissolving the potassium salts in the cryosolvent at the desired w/v composition. Cryobuffers were prepared at pH 7 by titrating the stock monobasic cryosolution with the stock dibasic cryosolution. IHP (50 μM) was included in the cryobuffers to ensure that the hybrid is in the T-conformation28 and 100 mM sodium azide was included to ensure that the hybrid remains in the azidomet form. The viscosities of the glycerol/water solutions were taken from tables.47 Sucrose/water cryobuffers were prepared similarly, with the viscosities also taken from tables.48
Samples for ET measurements were prepared in the dark under nitrogen. Small volumes of an aqueous stock solution of the azidomet hybrid were added to the anaerobic cryobuffer with a gastight syringe. Protein concentrations were determined spectrophotometrically using a diode array spectrophotometer (Agilent): ∈(424 nm) = 166 M-1cm-1 for the [α(Zn), β(FeCO)] derivative.49
Laser Flash Photolysis
In a simple photocycle, laser-flash excitation of the Zn porphyrin (ZnP) to its lowest excited triplet state (T) initiates ET to the Fe3+ with an ET rate constant, kt; this forms the charge-separated intermediate complex (I) which subsequently returns to the ground state with ET rate constant, kb, Scheme 1. In the absence of ET the 3ZnP decays with the intrinsic decay rate constant, kD. T decays exponentially with decay constant, kp = kt + kD; I appears with rate constant kb and disappears with kp. Flash photolysis measurements were made with an LKS60 photolysis unit (Applied Photophysics) equipped with a pulsed Xe arc lamp (75 W). Samples were excited with pulses from the second harmonic (532 nm, > 60 mJ, 10 ns) of a Q-switched Nd:YAG laser (Continuum). Triplet decays were monitored as absorbance changes at 475nm; absorbance changes of the ET intermediate, I, were monitored at ~ 440nm, the triplet/ground isobestic. Typically 10-25 transients were averaged for triplet decays and 100 transients for intermediate signals. For initial analyses triplet decays and the progress curves for I were fit to the equations for simple decay to of T to ground through the intermediate, T ⇒ I ⇒ G,
| (1) |
| (2) |
(kp = kt + kD) using either Sigma Plot or lab-written routines.
Kinetic Modeling
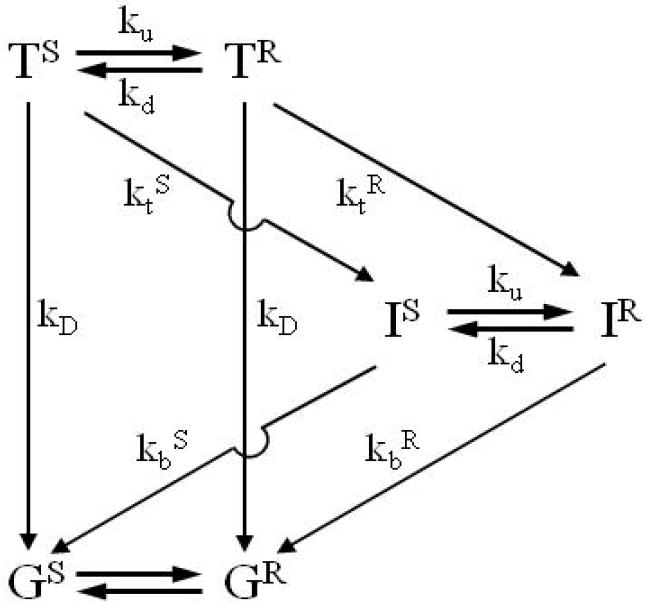
For comparison of experiment and simulations with the KD model, presented in Results and illustrated in Scheme 2, we either used the solution to the differential equations for Scheme 2 that were presented previously6 and are repeated in Supporting Information., or generated progress curves for the electron-transfer intermediate (I) and its component species (IR and IS) by constructing the KD kinetic model of Scheme 2 with the Simulation Control Program (ScoP, version 3.51) available from Simulation Resources, Inc; the overall progress curves are identical.
Scheme 2.
RESULTS
I. Kinetic-Dynamic (KD) Model for Conformational Control of ET
Conformational Kinetics
Consider a protein-protein ET complex that functions on an idealized energy landscape that has many (NS) poorly/non-reactive conformations, Si; and a smaller number (NR) of highly reactive ones, Rj, (Fig 1). The conformations are presumed to partition into two populations because the minority of ET-optimized Rj conformations are distinguished by a shorter ET distance24,50-54 and/or the presence of effective pathways created by specific H-bonds;55 together, such effects would introduce a ‘conformational reactivity filter’.
The kinetic equations for conformational interconversion between Rj and Si can be written in terms of conformational conversion rate constants, , ,
| (3) |
In applying these equations and linking them to an ET photocycle we shall take the members of each population to be equivalent by constraining them to have the same conformational energy, the same average rate constant for conversion to members of the other population, and the same rate constants for forward and back ET.56 This leads to landscapes such as the simple one illustrated by Fig 3A for NR = 1, NS = 7; an ET complex would be characterized by three such sheets, one for each of the excitation/redox states: k = T (photoexcited triplet); I (ET intermediate); G (ground).
Figure 3.
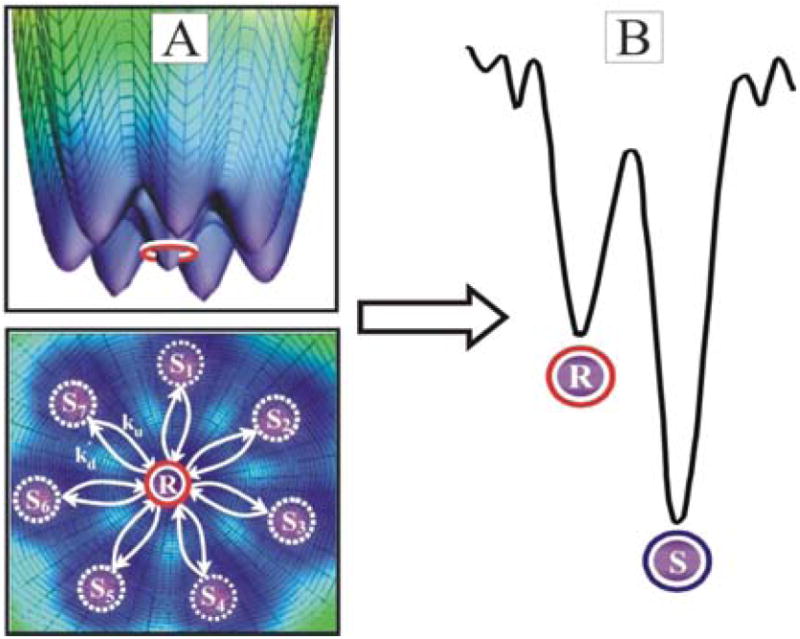
(A) Two views of a 3D energy landscape with Rj = 1 and seven equivalent Si conformations; rate constants for conversion from Si to R and R to Si, ku and kd respectively. (B) Gating energy landscape; S = ΣSi and R = ΣRj.
By summing Eq 3 (right) over j and Eq 3 (left) over i, defining total R and S populations as S = ΣSi, R = ΣRj, and inserting R, S into Eqs 3, these become differential equations for the R and S populations,
| (4) |
upon use of the constraint that each conformation within a population has the same average rate constants, kd and ku, for conversion to the other,
| (4a) |
These equations map the ensemble of interconverting Rj and Si configurations of state k onto the simple 2-D energy surface for two substate populations, R and S, Fig 3B. The equilibrium ratio of S configurations to R becomes:
| (5) |
where ES and ER are the energies of the S and R configurations, R the ideal gas constant, and T the temperature. Eq 5 further recognizes that the ratio, NS/NR, corresponds to a configurational entropy difference: ΔSRS = Rln(NS/NR), and defines a Helmholtz free-energy difference between populations, ΔARS = ΔERS -TΔSRS, which typically will differ little from the Gibbs free-energy difference: ΔGRS ≈ ΔARS. With the appropriate choice of conformational parameters this surface can describe the full range of energy landscapes and full spectrum of ET-coupled dynamics.
Conformationally coupled ET
As described in the introduction, to explicitly generate equations for conformationally coupled ET, we assume that ET rate constants are the same in each member of a population, but differ between populations because they exhibit different ET pathways.24,55 The [TR, TS] populations are assigned ET rate constants [ktR, ktS]; the [IR, IS] population are assigned rate constants [kbR, kbS]. A possible coupling between excitation/redox state and conformational dynamics is allowed for by allowing the interconversion rate constants to depend on the state: [kdT, kuT] and [kdI, kuI]. The resulting kinetic-dynamic (KD) scheme for the photocycle (Scheme 2) incorporates interconversions between reactive (R) and slow (S) conformational populations in each of the three excitation/redox states: G, T, and I; the corresponding differential equations are:
| (6) |
| (7) |
| (8) |
| (9) |
with kD being the triplet decay constant in the absence of ET.
The solutions to Eqs 6-9 were given earlier6 and for convenience are repeated with the current notation as Supporting Information. The decay curve of the photo-generated triplet (T = TS + TR) is a biexponential:
| (10a) |
The associated progress curve of the ET intermediate (I = IS + IR) is a sum of four exponentials in which two of the rate constants correspond to the triplet-decay rate constants (f and g) and two correspond to back rate constants (m and n).
| (10b) |
The progress curve for T can be decomposed into the individual curves for the conformational species, TR and TS; likewise, the progress curve for I can be decomposed into those for IR and IS. Alternatively, the function I(t) can be decomposed into at most three kinetic phases of the form of Eq 2, although these do not, in general, correspond to the progress curves of an individual species.
The four rate constants of Eqs 10 (f, g, m, and n) and the coefficients (ax and cy) of their exponentials are functions of both the four microscopic ET rate constants (ktS, ktR, kbS, and kbR) and the constants which describe the dynamics of the system.(Supporting Information) Each sheet of the energy surface is characterized by two independent dynamic parameters, which we choose to be kd and KS = kd/ku, defining ku = kd/KS. For simplicity, for the remainder of this report we take the conformational rates and equilibrium constants to be independent of excitation/redox state (kdT = kdI = kd, kuT = kuI = ku, and KST= KSI = KS) in which case the model employs only two independent conformational parameters, kd and KS.
We finally note that while the KD model as embodied in Eqs 6-9 is defined in terms of the temporal evolution of electronic/conformational populations or ‘species’ – the S and R conformational populations of the T and I (and G) electronic states – Fig 1 was inspired by the complementary picture of a conformationally controlled competition between different ET ‘routes’, where a route comprises the sequence of excitation/redox/conformational states through which the system passes during an ET photocycle. As we discuss below, the limiting cases and important regimes of Eqs 6-9 display four ET routes of particular interest (Fig 4).
Figure 4.
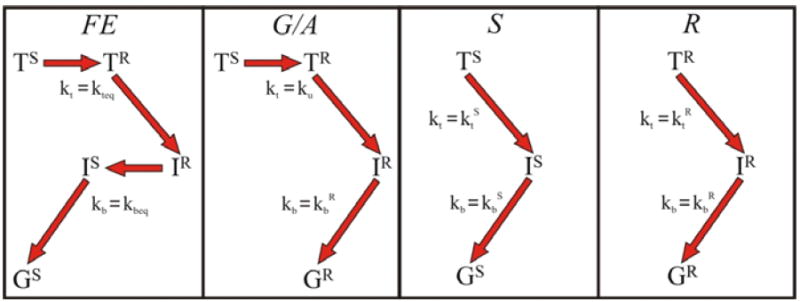
Kinetic routes implicit in Scheme 2 that contribute to the ET photocycle.
Detectability
Contributions of the two component phases to an experimental triplet decay curve are simply determined by their relative weights (which are not necessarily identical to their statistical populations). However, the contribution of a component kinetic phases to an experimental progress curve for I, which is best thought of as its maximum amplitude, does not simply correspond to its weight, for it is strongly influenced by the relative values of the rate constants for the appearance and disappearance of the phase. This is discussed in detail in the Supporting Material, and is of great importance in determining the appearance of experimental curves, as noted below.
II. Modulating Interconversion Dynamics
The final link between the KD model and a system in which ET kinetics are coupled to conformational interconversion is to fix the function that relates interconversion rates and solution properties. When viscosity is the important solution variable we may take changes in viscosity as affecting ku and kd equally, leaving KS invariant, and write the ku and kd in the Kramers-like form,57-59
| (11) |
although alternate forms are available.60,61 If osmotic effects are important the kd,u0 become functions of the molality of the solute. They also are functions of the number of waters released during the conformational changes, so osmotic effects can change the two rate constants differently, and hence change KS. We show below that Eq 11 is applicable to data for the Hb hybrids.
III. Limits and Regimes
If the properties of the KD model of Eqs 10, 11 are examined over ranges of the controlling parameters, one finds a quite complicated ‘phase diagram’ comprised of distinct regimes (parameter ranges) of dynamical behavior. Considering the forward and back ET processes individually, one recognizes known regimes such as the fast-exchange (FE) and slow-exchange (SE) limits, as well as the gating (G) regime for forward ET. When examining the complete photocycle, limiting behaviors also appear, but novel ones also arise. To facilitate analysis of the experimental results for the hybrids we briefly describe the two limiting photocycle regimes, as well as one in which back ET is initiated within a non-equilibrium ensemble of conformers as envisaged in Fig 1. It is important to emphasize that such limits/regimes are not simply characteristics of an ET system, but represent the behavior of a system whose coupling between ET and conformational dynamics has been ‘tuned’ by a particular set of solution conditions. In general, variations of temperature/viscosity/osmotic pressure/pH/ionic strength can shift the system smoothly from one regime to another along a continuum of behaviors, while mutations can shift it discontinuously.
(i) Fast Exchange Photocycle
In the fast-exchange (FE) limit for forward ET, [ku, kd] ≫ [ktR, ktS], the S and R populations interconvert so rapidly that equilibrium populations are maintained at all times. The decay of T is described by a single forward ET rate constant kteq, with observed decay constant kobseq = kD + kteq, where kteq is a weighted average of ktS and ktR,
| (12) |
The weighting factors (FS and FR) correspond to the equilibrium fractional populations of the S and R substates. In the FE limit for back ET, defined by [ku, kd] ≫ [kbR, kbS], the IR and IS populations also interconvert so rapidly that an equilibrium ratio of these conformers is maintained throughout the progress curve for I and back ET also is described by a weighted average of the back ET rates for the individual conformational ensembles, kb = kbeq,
| (13) |
As a result, for the FE photocycle, in which both forward and back ET are in the FE limit, the progress curve for I is described by a single kinetic phase (Eq 2) with average ET rate constants, kteq and kbeq.
The ‘conformationally coupled’62 photocycle has the same type of dependence on ET driving force as if ET took place on a simple landscape, as kteq and kbeq are proportional to microscopic ET rate constants. However, the photocycle has observed ET rate constants that are independent of the individual conformational rate constants. Thus, within the limit, a change in viscosity would have no effect on the photocycle and would not reveal the presence of coupling between ET and conformational dynamics.
The dominant route in the FE photocycle depends on the explicit values of the rate constants. We show below that for the Hb hybrid at low viscosity the microscopic rate constants correspond to a well-defined majority ‘FE route’ for ET (Fig 4): TS ⇒ TR ⇒ IR ⇒IS ⇒G.
(ii) Slow Exchange Photocycle
The opposite, slow-exchange (SE), limits for forward and back ET occur respectively if [ku, kd] ≪ [ktR, ktS] and [ku, kd] ≪ [kbR, kbS]. If both forward and back processes are in SE the R and S populations react independently, with their own forward and back ET rate constants, and with weights/‘yields’ of the two phases of T(t) and I(t) simply given by the equilibrium populations, [FS, FR]. The photo-excited R hybrids follow the ‘R-route’ (TR ⇒ IR ⇒ G); photo-excited S hybrids follow the ‘S-route’ (TS ⇒ IS ⇒ G) (Fig 4). As with the FE photocycle, the ET rate constants in the SE photocycle depend on ET driving force and, of course, are independent of viscosity.
(iii) Photocycle with a Non-Equilibrium Distribution of I
Situations of this type arise when forward ET is in the gating (G) regime, which occurs when [ktS ≪ ku < kd ≪ ktR]. The observed decay rate of T then is determined by the rate of conformational conversion, kobs = ku + kD, not an ET rate. As a result, this rate constant varies with addition of viscogen, not with changes in ET driving force. In principle, the decay of T actually is biphasic, with the small fraction FR forming TR upon laser excitation and promptly decaying with the viscosity independent rate constant, kobs = ktR + kD. However, for KS ≫ 1 (ku ≪ kd), FR ≪ 1 and the contribution of this ‘prompt’ or ‘burst’ phase is small.
When forward ET is in the G regime the major route for forward ET produces the IR conformer, even though the R conformation is highly disfavored by a large value of KS. As a result, the back reaction begins in a non-equilibrium state, as envisaged in Fig 1. If the conformational deactivation of IR is slower than back ET from IR (kbR ≫ kd), then IR undergoes IR ⇒ G back ET without conformational deactivation to IS and the observed back ET rate constant will be kbR. We call this back ET regime ‘anti-gated (A)’ because the relative importance of the IR ⇒ G process is governed by the value of kd, a conformational rate constant, yet this back ET step occurs with an ET rate constant which varies with ET driving force, unlike gated (G) forward ET.
With the gating and anti-gating inequalities both satisfied, the majority of the complexes follows the route, TS ⇒ TR ⇒ IR ⇒ G (G/A route in Fig 4), which precisely corresponds to the photocycle schematized in Fig 1: the forward ET process occurs from an initial equilibrium ensemble, while the reverse ET process occurs from a non-equilibrium ensemble, with conformational dynamics controlling both ET processes. As noted above, if the R population is not vanishingly small there would be a second, minority route: the fraction FR of complexes that are photoexcited to the TR state would undergo ‘prompt’ ET along the R-route (Fig 4): TR ⇒ IR ⇒ G.
IV. Modeling Experimental Data for the [α(Zn), β(FeN3-)] hybrids
Figure 5A shows representative progress curves for the appearance and disappearance of the ET intermediate, I, as the range of viscosities, η = 1→15 cP is traversed by addition of either glycerol or sucrose at 20° C. The most apparent change in the curves with increasing η is an ~ 60% decrease in the maximum absorbance of I (ΔAmax). In addition, a concomitant shift of ΔAmax from 7.5 ms to 5.1 ms reflects an apparent increase in the rate of appearance of I and a decrease in the rate of its disappearance.
Figure 5.
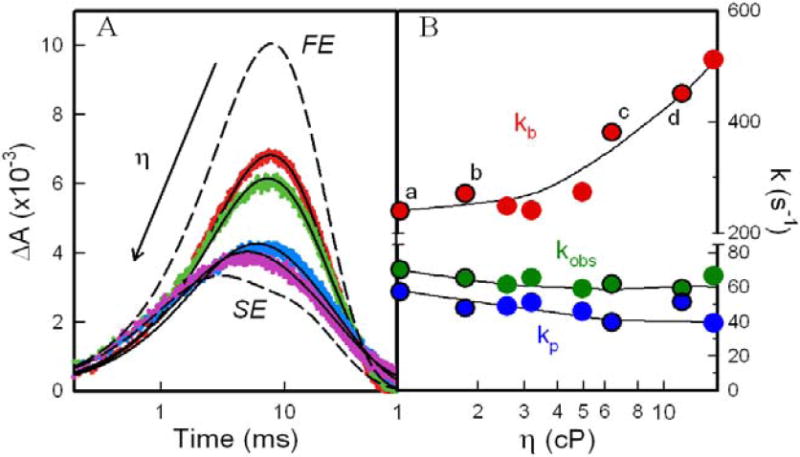
(a) Experimental progress curves of I for [α(Zn)β(Fe)(N3-)] at η = 1 cP (red), η = 1.7 cP (green), η = 6.3 cP (blue), and η = 12 cP (purple); overlaid lines represent fits to Eq 2 for a relaxed photocycle, kobs ≠ kp. The agreement between the long-time tails of the experimental and calculated traces has been slightly improved by inclusion in the latter of a slight contribution from [α1(ZnP+)β2(Fe3+)/α2(ZnP)β1(Fe2+)] dimer pairs that form by dissociation of tetrameric I; these do not recombine to tetramers and undergo back ET on the timescale of these experiments (Supporting Information). (b) ET rate constants, kb (red), kp (blue), and kobs (green) as a function of η for a relaxed photocycle: kobs from fits of T to Eq 15; kb and kp from fits of timecourse for I to Eq 15. Lines are to guide the eye.
Attempts to fit the viscosity dependence of the progress curves for T and I to the equations for the simple photocycle of Scheme 1, Eqs 1,2 (Fig S1), with viscosity-independent value values for [kd, kb] fail (Fig S1). The calculated and experimental decays of I differ substantially even at η = 1 cP, with the discrepancy being biggest in the appearance of I, and the discrepancy gets progressively worse as η increases. This behavior implies the type of coupling between conformational dynamics and ET embodies in the KD model. Application of this model to the hybrid dataset involves determination of the microscopic parameters in Scheme 2 optimize the description of the progress curves for both T and for I.
There are seven KD parameters in Scheme 2, but the intrinsic decay constant (kD = 50±5 s-1) is known from independent measurements of the triplet decay for the [α(Zn), β(Fe2+)] hybrid].63 This leaves four microscopic ET rate constants (ktR, kbR, ktS, kbS) and two conformational variables, KS and kd, to be determined. For simplicity we take the conformational rates and equilibrium constants to be independent of excitation/redox state, which means that each trace is described by two independent conformational variables: the viscosity-invariant conformational equilibrium constant, KS; kd for that trace/viscosity. Upon determination of a kd for each viscosity/trace, a fit of this set of parameters to Eq 12 provides a global description of the viscosity dependence in terms of three conformational parameters: KS, kd0 and α.
Direct determination of these parameters by a direct, global least-squares fit to a set of progress curves for T and I generated over a range of viscosities would not be instructive and might not be wholly credible; fortunately, it is not necessary. Instead, we have devised a rapidly converging, iterative procedure that begins by approximating the microscopic ET constants and generating four constraints; this reduces the problem to a determination of KS for the system, kd at each viscosity and their subsequent use to parameterize Eq 11.
We began the analysis by first fitting the progress curves to the kinetic equations for a “relaxed photocycle (RP)”, defined through a rewriting of Eqs 1,2:
| (14) |
| (15) |
with kobs = kt + kD. These differ from Eqs 1, 2 in that the triplet decay constant, kobs, is not required toequal a rate constant associated with I, and is replaced by an additional fitting parameter associated with an individual trace, kp. This approach, which we have used before,5,27,32,34 provides a useful, heuristic description of the progress curves, as shown by the moderately successful overlay of calculated and experimental traces in Fig 5A. There is, however, no kinetic scheme which gives rise to these heuristic equations.
Fig 5B plots the η dependencies of the parameters, [kobs, kb, kp], obtained in this fashion. It shows that [kobs, kp] decrease modestly, while kb increases two-fold as η is increased with either viscogen. When the ET rate constants for the datasets obtained through the addition of glycerol and of sucrose are plotted versus viscosity and molality (Fig S2), only those plotted against viscosity show a correlation for the two solutes, consistent with our earlier suggestion5,27 that the dynamics are responding to viscosity rather than osmotic effects.64-66 Thus, the RP model of the photocycle at fixed temperature confirms that the forward and reverse ET processes respond differentially to changes in conformational dynamics caused by addition of viscogen, even though there is no kinetic mechanism which would produce the equations that define the RP model, Eqs 14,15.
Four initial constraints on the KD model were derived from the plots of kt (kt = kobs - kD) and kb (Fig 5B), by provisionally assuming that the behaviors at low and high viscosity approach the FE and SE limits, respectively. The values of [kt, kb] at the highest viscosity employed (η = 15 cP) were extrapolated (by eye) to yield approximations for two of the four microscopic ET rate constants: ktS = 5s-1; kbR = 500s-1. The values of [kt, kb] at the lowest viscosity (η = 1 cP) were taken as estimates of the FE rate constants: kteq = 18s-1; kbeq = 230s-1. Eqs 12,13 were then inverted to obtain expressions for the two remaining microscopic ET rate constants (ktR and kbS) as functions which incorporate the four constraints as parameters (ktS, kbR, kteq, kbeq) and have KS as the one independent variable.
If a value of KS is specified for the dataset of traces collected over a range of viscosities, the optimized values of kd for each progress curve of I then completes a set of microscopic constants that can be input into the KD model and used to simulate this curve either through direct use of Eq 10 or with the SCoP package. At this initial stage, we used as “goodness-of-fit” criteria, the time at which the concentration of I was maximal (τmax) and the ΔAmax at that time. These features were readily reproduced with a globally optimized KS for the set of traces and individual values of kd for each trace; these latter then were used to parameterize Eq 11. The values for the constraints and the resulting initial set of KD parameter are compiled in Table 1.
Table 1.
KD Parameters that Describe the [α(Zn), β(Fe3+N3-)] ET Photocycle.
| Parameter | Initial | Final |
|---|---|---|
| kteq (s-1)a | 18 | 21 |
| kbeq (s-1)a | 230 | 210 |
| ktS (s-1)a | 5 | 5 |
| ktR (s-1) | 409 | 517 |
| kbS (s-1) | 221 | 200 |
| kbR (s-1)a | 500 | 550 |
| KS | 30 | 31 |
| α | 0.83 | 0.91 |
| kd0 (s-1) | 3000 | 1017 |
Constraints generated as described in text
Next, we refined these values by iterating the constraints. The hybrid cannot be poised completely into the FE limit at η = 1 cP, because if it were then Eqs 1, 2 would be adequate to describe the at η = 1 cP progress curves, but as stated above this is not so. Therefore, the rate constants obtained by fitting the progress curves of T and I at η = 1 cP to Eqs 14, 15 provide only a lower bound to kteq (18s-1) and an upper bound to kbeq (230s-1). We refined the constraints by systematically increasing kteq and decreasing kbeq while further varying the extrapolated value for kbR. At this final stage, goodness-of-fit was determined by the ability of the simulations to accurately reproduce the complete timecourses of I.
This iterative exploration of parameter space quickly converged to a set of four values for the constraints, none of which differ from the original set of four by more than ~10% (Table 1). The progress curves calculated for I with the final set of KD parameters are in excellent agreement with the experimental curves, as shown in Fig 6A-D for four different viscosities. In particular, the early-time ‘rise’ of the intermediate signal is improved by the iteration (Fig S3). Fig 6E shows how the traces for I evolve as the dynamics progressively traverse the full range from FE to SE, relating them to experiment by including the traces for the lowest and highest viscosities studied. This figure clearly shows that at η = 1 cP the system does not approach FE, while at η = 15 cP it is rather near to SE.
Figure 6.
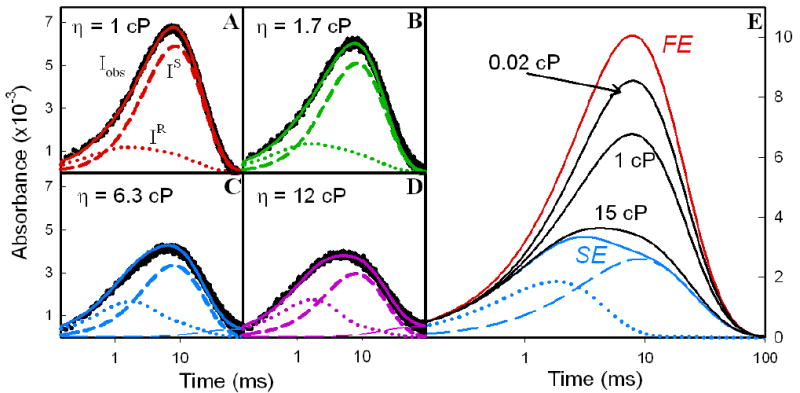
(a-d) Experimental I timecourses (black) at η = 1, 1.7, 6.3, and 12 cP overlaid with simulated KD traces (solid lines) calculated with final parameters in Table 1. Below each trace is its decomposition into conformers, IS (short dashed line) and IR (dotted line). As in Fig 5A, agreement between the long-time tails of experimental and calculated traces requires a slight contribution from [α1(ZnP+)β2(Fe3+)/α2(ZnP)β1(Fe2+)] dimer pairs that form by dissociation of tetrameric I; these do not recombine to tetramers and undergo back ET on the timescale of these experiments (see Supporting Information). (e) Evolution of I progress curves from FE limit to SE limit; calculations use final parameters in Table 1.
Decomposition and Analysis of Simulated Hybrid Progress Curves
In addition to showing the experimental and final calculated progress curves, Fig 6 gives decompositions of I(t) into the progress curves of the IR and IS components for η = 1, 1.7, 6.3 and 12 cP; Fig 6E shows the analogous decomposition for the extrapolated SE limit. These decompositions show that the major consequence of increasing η is the suppression of the IS phase as a slowing of conformational conversions suppresses the S → R transition. Other consequences include: an increasing importance and sharpening of the IR phase, with ΔAmax increasing slightly and shifting to earlier time; the appearance of a ‘tail’ associated with IS becomes visible at longer times. The increased importance of IR relative to IS corroborates our intuitive expectation that I is largely formed as the reactive conformer (IR) and that increasing the viscosity slows the conversion to the less-reactive conformer (IS) thereby increasing the contribution of a fast return to ground within the IR conformation.
The fact that the fit to the experimental progress curves has significant contributions from two kinetic phases with quite different time courses explains why even the relaxed photocycle model does not adequately describe the results, most especially failing to match the curves for I at elevated viscosities (Fig 5A): in any ‘simple’ photocycle I(t) is necessarily a single kinetic phase. The similarity of the forward and back ET rate constants for the R population (Table 1) is expected, as the driving forces for the two reactions are similar.67
The values of the forward ET rate constants differ from each other by approximately two orders of magnitude (Table 1, ktR = 550 s-1 and ktS = 5 s-1), while the back ET rate constants differ only by a factor of ~2.5 (kbR = 517 s-1 and kbS = 200 s-1); further, the forward and back ET rate constants for the S population (Table 1) differ appreciably. We speculate that these difference reflects a limitation of the two-population approach. The large difference in the forward rates may occur because the system is distributed over all phase space prior to excitation, with the majority in a slow configuration, while the smaller difference in the back ET rate constants suggests that the system samples a much more limited volume of phase space before returning to the ground state by back ET. In addition, these effects may reflect conformational averaging on a more rapid timescale that differs between the populations.
DISCUSSION
The Hb hybrids provide a convenient system with which to explore dynamic control of an ET photocycle within a pre-docked protein-protein complex, and we have examined how the hybrid photocycle responds to changes in conformational dynamics induced by changes in viscosity at fixed temperature. This photocycle exhibits ‘differential dynamics’ in the sense that a fit of the progress curves for T and I to the ‘relaxed photocycle’ of Eqs 14, 15 showed that as η increases and conformational dynamics slow, the apparent forward ET rate constant decreases while the apparent back ET rate constant increases, Fig 5B.5,27 However, the progress curves for I in fact are not well fit by this model, Fig 5A, and in any case the model is inadequate in that it does not explicitly incorporate conformational processes and represents no underlying kinetic mechanism. As a result we have developed the simple ‘KD’ model for the ET photocycle of a system in which ET is coupled to conformational dynamics and applied it to the viscosity dependence of the [α(Zn), β(Fe3+N3-)] hybrid photocycle.
The model assumes the complex exists as multiple interconverting conformations. These partition into two populations, NR reactive conformations, R and NS non(poorly)-reactive S (Fig 3B) because the R conformations are ET-optimized by a shorter ET distance and/or the presence of effective pathways created by the presence of specific H-bonds. Taking the conformations within a population to be equivalent imposes the constraint that the members of each population have the same average rate constant for conversion to the other along the single (effective) conformational coordinate (Eq 4a). Fig 3A illustrates the underlying energy landscape for the simple case, NR = 1, NS = 7. The solutions of the resulting differential equations for the KD model of a conformationally-coupled ET photocycle (Eq 10; Supporting Information) were presented previously and their application to forward ET discussed in detail.6 However, their general applicability was not recognized, and their application to a full ET photocycle was at best rudimentary.
Examination of the solutions showed they can describe the full spectrum of ET-coupled dynamics through an appropriate choice of the difference in ensemble energies, ΔERS, of the ratio of the number of members of R and S ensembles, NS/NR, and of relative values for ET and conformational kinetic rate constants. As conformational interconversion is ‘turned on’ the model leaves the limit (SE) in which dynamics play no role, either because only a single state or population is energetically accessible or because conformational changes are much slower than ET. It passes through a ‘gating/anti-gating’ (G/A) regime, in which the two conformational populations convert on a time-scale competitive with ET, arriving at a limit in which ET occurs within a conformationally averaged state (FE) in which the timecourses of both T and I are monophasic. The model further can describe the ‘Dynamic Docking’ regime, in which phase-space control of ET in a weakly-bound complex is engendered by a landscape with numerous conformations of similar energy, only a few of which are ET-active (NS ≫ NR).
The analysis further led to the recognition that when treating intermediate dynamic regimes, it is instructive to consider not merely the timecourses of the states involved, T and I, but also the routes by which a complex evolves from its initial triplet conformation to the ET intermediate, and finally back to the ground conformation, a route being defined as the sequence of excitation/redox/conformational states traversed during this process. Fig 4 illustrates routes associated with the FE and SE limits, but it also illustrates a particularly interesting route traversed when the conformational and ET rate processes compete. Under conditions when the forward ET reaction is gated and the back ET process ‘anti-gated’, I can follow the GA route, TS ⇒ TR ⇒ IR ⇒G, which corresponds closely to the intuitive idea of a photocycle in which the forward reaction occurs from an equilibrium ensemble of conformations but the back reaction occurs from a non-equilibrium reactive ensemble, Fig 1.
Such consideration of ET routes highlight the fact that ET reactions in conformationally mobile systems provide a ‘clock’ against which the rapidity of a dynamic event is measured, and that each ‘branch point’ in a route represents a competition between an ET and conformational process. In addition to direct deactivation to ground, the triplet populations of Scheme 1 each have two channels for reaction, one ET and one conformational, [TS ⇐ TR ⇒ IR], [TR ⇐ TS ⇒ IS]; each of the populations of I has only two, [IS ⇐ IR ⇒ G], [IR ⇐ IS ⇒ G]. The partition of each state into the alternate reaction channel is determined by the relative values of the respective competing ET and conformational rate constants. As there are four ET rate constants in the two-population KD model, Scheme 1, all of which can in principle differ, there are four ‘clocks’ and the photocycle overall should be sensitive to motions on the four timescales set by them. As the rate constants for the effective conformational coordinate are progressively slowed with increasing viscosity the partitions at the four branch points should progressively respond, starting with the branch point that has the largest ET rate constant. Regarding the two T populations, one must further note that if an ET rate constant is not much larger than kD, then direct deactivation provides the clock against which conformational events must compete.
The KD Model and the ET Photocycle of the Hb hybrids
As a first application of the KD model we analyze the viscosity dependence at 20°C of the ET photocycle of the pre-docked [α(Zn), β(Fe3+N3-)] hybrid, Fig 6. Measurements performed with glycerol and sucrose as solutes give equivalent results when correlated by solution viscosity, not solute molality, which supports the earlier suggestion that solutes indeed exert their influence on viscosity, rather than through osmotic effects.68-70 A robust, iterative procedure for fitting the model to experiment has been devised and simulations of the hybrid ET photocycle based on the resulting ET and conformational parameters reproduce experiment quite well across the range of viscosities (Fig 6;Table 1).
The timecourses for the hybrid at 20°C are well described with the model’s assumption of two conformational populations, the minority ensemble being more ET active. Comparison of the experimental and calculated progress curves for I shows that the trace for η = 1 cP deviates appreciably from that for the FE limit, Fig 6E. Beginning with η = 1, and through most of the viscosity range, multiple routes contribute to the timecourse for I and this precludes simple analysis; we do note significant involvement of a route involving gated forward ET and conformational coupling in the back. By the highest viscosity employed, η = 15 cP, the simulated trace (Fig 6E) suggests that the photocycle is close to the SE limit, but in fact there is still a significant contribution from the G/A route (Table S3). The fraction of TS that follows the S route produces IS, while the remainder of the TS population that follows the G/A route produces IR. The small amount of TR formed directly by flash excitation, FR, undergoes ‘prompt’ ET along the R route; this process, which is similar to that for TR in the SE limit, does not contribute significantly to the triplet decay, but is important for the progress curve of I. The total fraction of back ET that proceeds along routes that pass through IR is given by the sum of the contributions from ‘prompt’ ET along the R route and from the G/A route (ϕR + ϕG/A). This increases from 8% in the FE limit to 49% at η = 15 cP, and then decreases to ϕR ~ 24% as the contribution of the G/A-route falls to zero (ku ⇒ 0) and the SE limit is reached, Table S3.
Nature of the ET-coupled Motions in the [α(Zn), β(Fe3+N3-)] Hybrid
The KD analysis of the hybrid ET photocycle shows that the ET-coupled motions are fairly slow, kd < 103s-1; what are they? Hb is the archetypical allosteric protein, and Hb allosteric conformational rearrangements occur on the microsecond – second timescales.71 Our current hypothesis is that ET is coupled to the large-scale allosteric motions which play an integral role in the O2-binding mechanism of the Hb tetramer.43 In recent years it has been shown that the low-affinity ‘T’ and the high affinity ‘R’ structures of Hb are in fact ensembles of structures, and within each there is a near-continuous variation in structure.40,41,72 The [α(Zn), β(Fe3+L)] hybrid behaves as a diliganded T tetramer,28,35,73,74 One possibility is that the ET-coupled motions involve conversions between ensembles, and in fact T →R conversion rates for diliganded hybrids fall into the range of interest here.75,76 Alternatively the conversion could be within the T ensemble. In either case, an accompanying change in the contacts at the interface between the [α1(Zn), β2(Fe+3N3-)] ET partners upon conversion between S and R configurations would lead to the differing ET reactivities of S and R. Perhaps these changes might involve the formation and collapse of an inter-subunit network of H-bonded waters, as has been proposed for inter-protein ET in other systems.52 Future experiments will test these ideas through the study of Hb hybrids in the presence of allosteric effectors,77-79 and of hybrids prepared with mutations at the α1/β2 interface,80,81 both of which systematically alter the allosteric conformational equilibria/dynamics
Benefits of a Photocycle
Although numerous studies have described conformational control of a ‘forward’ ET reaction that is initiated either by rapid mixing or by photolysis,60,82-90 the results for the hybrid and their analysis with the KD model illustrate the benefits of studying a photocycle when possible. The simplest one is practical and diagnostic. In the absence of conformational influences the timecourse of I necessarily is a single ‘rise-and-fall’ kinetic phase that is self-consistently tied to the decay of T through its decay constant, Eqs 1, 2. The simple observation either of a lack of consistency (different kobs, kp, Eqs 14, 15) as shown for the hybrids in Fig 5B, or of the need to fit I(t) with multiple kinetic phases91 implies conformational influences even before performing measurements as a function of η. For the hybrids, not only are multiple phases needed to describe I(t) without addition of viscogen, but the η dependence of the timecourse of I gives additional indications of ET coupling to conformational dynamics, including: i) a shift in ΔAmax to shorter time and decrease in maximum absorbance change as η is increased; ii) poor fits of the actual progress curves even to the ‘relaxed photocycle’ model, Eqs 14, 15.
Specific analysis highlights the limited ability to characterize both the ET and conformational processes when only the kinetics for the photoinitiated ‘forward’ reaction are studied. When the timecourse of T can be studied throughout the entire dynamic range from FE to SE by variation of viscosity, and both kinetic phases of Eq 10a, can be observed, it is possible to obtain all the ET and conformational constants for the forward reaction. If, however, the timecourse of T is essentially monophasic over the accessible range of η, as is true for the hybrid, then only some of the parameters are accessible. i) If T is independent of η throughout the accessible range of η, it could be that there is no conformational coupling, but also it could be that the system is in FE throughout the range. In this case the measured rate constant is a conformationally weighted average of microscopic ET constants and conformational coupling is masked. ii) If, on the other hand, kobs for the single phase simply decrease with increasing viscosity, reaching a limiting value at high η, then one can only assume that the decay of T corresponds to the decay of TS, which involves a competition between deactivation to ground, ET from this state, and gated ET governed by the conformational conversion to TR. In this case,
| (16) |
with ku(η) = kd(η)/KS. A fit of kobs (η) with kd(η) given by Eq 11 would then give values for [ktS, kd0, α], as kD is known. In the case of the hybrids, kobs does decrease with η (Fig 5B), and a fit to Eq 16 gives [ktS, ku0, α]; ktS and α are within ten percent of those from the KD fit (Table 1), while ku0 is within a factor of two. Thus treatment with Eq 16 indeed is useful in defining the role of conformational coupling on forward ET through determination of values for [ktS, ku0, α]. However, measurements of forward ET never can verify that the gating inequalities given above are satisfied, and in fact the KD analysis of the hybrid photocycle shows that the key requirement, [kd ≪ ktR], is violated at low viscosities, kd(1 cP) = kd0 = 1017 s-1 > ktR = 517 s-1; thus the assumption leaves a false impression about the values of kd0 and ktR. This treatment naturally cannot give the remaining four parameters that come from treatment of the back reaction in the KD model, [ktR, kbS, kbR, kd0 or KS].
Applicability of the KD model
We have shown that this model can describe the full ‘phase diagram’ of ET-coupled dynamics through an appropriate choice of parameters, but one must consider what is lost by the restriction to a single effective conformational coordinate. Within the model the decay of T is biexponential under all conditions except FE, while the timecourse for I can be decomposed into at most three of the ‘rise-and-fall’ kinetic phases that each correspond to those of the simple photocycle of Scheme 1. If members of the R and S populations were not constrained to be equivalent, then the decay of T would be distributed, a characteristic of more complex models of ET.27-29,73 However, if the distribution of rate constants in a population is not too broad this difference is more apparent than real, as it would not be possible to distinguish between bi-exponential and distributed kinetics in T unless the experimental traces have exceptionally (and usually unreachably) high signal/noise ratios.92 Similarly it would be hard to convincingly establish that an experiment demands a more complicated equation for I(t), one decomposable into four or more kinetic phases or showing distributed behavior. We therefore suggest that the two-population KD model will usefully describe the basic features of ET coupled to dynamics in most photocycles, although in some experimental situations more complex models may well be required.
Supplementary Material
Fits to the simple photocycle of Scheme 1 (Fig S1), solutions to the differential equations for Scheme 2, variation of the RP fit parameters on molality (Fig S2), fits to the KD model generated with the initial parameter set (Fig S3), and modified version of Scheme 2 that incorporates dissociation of the Hb tetramer into dimers, discussion of yields and detectability factors with supporting tables (S1-S3).
Acknowledgments
This work was supported by the National Institutes of Health (HL63203).
References
- 1.Marcus RA, Sutin N. Biochim Biophys Acta. 1985;811:265–322. [Google Scholar]
- 2.Balzani V. Electron transfer in chemistry. Wiley-VCH: Weinheim; New York: 2001. [Google Scholar]
- 3.Hoffman BM, Ratner MR. J Am Chem Soc. 1987;109:6237–6243. [Google Scholar]
- 4.Liang Z-X, Nocek J, Huang K, Hayes RT, Kurnikov IV, Beratan DN, Hoffman BM. J Am Chem Soc. 2002;124:6849–6859. doi: 10.1021/ja0127032. [DOI] [PubMed] [Google Scholar]
- 5.Hoffman BM, Celis LM, Cull DA, Patel AD, Seifert JL, Wheeler KE, Wang J, Yao J, Kurnikov IV, Nocek J. PNAS. 2005;102:3564–3569. doi: 10.1073/pnas.0408767102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hoffman BM, Ratner MA, Wallin SA. In: Advances in Chemistry Series. Johnson MK, King RB, Kurtz DM Jr, Kutal C, Norton ML, Scott RA, editors. Vol. 226. American Chemical Society; Washington, D.C.: 1990. pp. 125–146. [Google Scholar]
- 7.Johnson MK, King RB, Kurtz DM, Kutal C, Norton ML, Scott RA. Electron Transfer in Biology and the Solid State: Inorganic Compounds with Unusual Properties. American Chemical Society; Washington, D.C.: 1990. [Google Scholar]
- 8.Kosek-Dygas MM, Hoffman BM, Matkowsky BJ, Nitzan A, Ratner MA, Schuss Z. J Chem Phys. 1989;90:1141–1148. [Google Scholar]
- 9.Davidson VL. Acc Chem Res. 2000;33:87–93. doi: 10.1021/ar9900616. [DOI] [PubMed] [Google Scholar]
- 10.Ivkovic-Jensen MM, Ullmann GM, Crnogorac MM, Ejdebaeck M, Young S, Hansson O, Kostic NM. Biochemistry. 1999;38:1589–1597. doi: 10.1021/bi9817156. [DOI] [PubMed] [Google Scholar]
- 11.Balabin IA, Onuchic JN. Science. 2000;290:114–117. doi: 10.1126/science.290.5489.114. [DOI] [PubMed] [Google Scholar]
- 12.Miyashita O, Okamura MY, Onuchic JN. Proc Natl Acad Sci U S A. 2005;102:3558–3563. doi: 10.1073/pnas.0409600102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Volkov AN, Worrall Jonathan AR, Holtzmann E, Ubbink M. Proc Natl Acad Sci U S A. 2006;103:18945–18950. doi: 10.1073/pnas.0603551103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bendall DS. Protein Electron Transfer. BIOS Scientific Publishers; Oxford: 1996. [Google Scholar]
- 15.Kang SA, Crane BR. Proc Natl Acad Sci U S A. 2005;102:15465–15470. doi: 10.1073/pnas.0505176102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jeuken LJC. Biochim Biophys Acta, Bioenerg. 2003;1604:67–76. doi: 10.1016/s0005-2728(03)00026-4. [DOI] [PubMed] [Google Scholar]
- 17.Toogood HS, Leys D, Scrutton NS. FEBS Journal. 2007;274:5481–5504. doi: 10.1111/j.1742-4658.2007.06107.x. [DOI] [PubMed] [Google Scholar]
- 18.Toogood HS, van Thiel A, Basran J, Sutcliffe MJ, Scrutton NS, Leys D. J Biol Chem. 2004;279:32904–32912. doi: 10.1074/jbc.M404884200. [DOI] [PubMed] [Google Scholar]
- 19.Crowley PB, Ubbink M. Acc Chem Res. 2003;36:723–730. doi: 10.1021/ar0200955. [DOI] [PubMed] [Google Scholar]
- 20.Wheeler KE, Nocek J, Cull DA, Yatsunyk LA, Rosenzweig AC, Hoffman BM. J Am Chem Soc. 2007;129:3906–3917. doi: 10.1021/ja067598g. [DOI] [PubMed] [Google Scholar]
- 21.Liang Z-X, Kurnikov IV, Nocek JM, Mauk AG, Beratan DN, Hoffman BM. J Am Chem Soc. 2004;126:2785–2798. doi: 10.1021/ja038163l. [DOI] [PubMed] [Google Scholar]
- 22.Sumi H, Marcus RA. J Chem Phys. 1986;84:4894–4914. [Google Scholar]
- 23.Medvedev ES, Kotelnikov AI, Goryachev NS, Psikha BL, Ortega JM, Stuchebrukhov AA. Molecular Simulation. 2006;32:735–750. [Google Scholar]
- 24.Kawatsu T, Beratan DN. Chem Phys. 2006;326:259–269. doi: 10.1021/jp052194g. [DOI] [PubMed] [Google Scholar]
- 25.Shihab MS, Kubota K, Takahashi T, Ohga Y, Asano T. Chem Lett. 2004;33:1542–1543. [Google Scholar]
- 26.Barzykin AV, Frantsuzov PA. J Chem Phys. 2001;114:345–354. [Google Scholar]
- 27.Patel AD, Nocek JM, Hoffman BM. J Am Chem Soc. 2005;127:16766–16767. doi: 10.1021/ja0552242. [DOI] [PubMed] [Google Scholar]
- 28.Blough NV, Zemel H, Hoffman BM, Lee TCK, Gibson QH. J Am Chem Soc. 1980;102:5683–5685. [Google Scholar]
- 29.Huang Y, Yonetani T, Tsuneshige A, Hoffman BM, Ackers GK. Proc Natl Acad Sci U S A. 1996;93:4425–4430. doi: 10.1073/pnas.93.9.4425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hui HL, Kwiatkowski LD, Karasik E, Colby JE, Noble RW. Biochemistry. 2004;43:7843–7850. doi: 10.1021/bi030263g. [DOI] [PubMed] [Google Scholar]
- 31.Samuni U, Juszczak L, Dantsker D, Khan I, Friedman AJ, Perez-Gonzalez-De-Apodaca J, Bruno S, Hui HL, Colby JE, Karasik E, Kwiatkowski LD, Mozzarelli A, Noble R, Friedman JM. Biochemistry. 2003;42:8272–8288. doi: 10.1021/bi020648j. [DOI] [PubMed] [Google Scholar]
- 32.Natan MJ, Kuila D, Baxter WW, King BC, Hawkridge FM, Hoffman BM. J Am Chem Soc. 1990;112:4081–4082. [Google Scholar]
- 33.Gingrich DJ, Nocek JM, Natan MJ, Hoffman BM. J Am Chem Soc. 1987;109:7533–7534. [Google Scholar]
- 34.Kuila D, Natan MJ, Rogers P, Gingrich DJ, Baxter WW, Arnone A, Hoffman BM. J Am Chem Soc. 1991;113:6520–6526. [Google Scholar]
- 35.Miyazaki G, Morimoto H, Yun K-M, Park S-Y, Nakagawa A, Minagawa H, Shibayama N. J Mol Biol. 1999;292:1121–1136. doi: 10.1006/jmbi.1999.3124. [DOI] [PubMed] [Google Scholar]
- 36.Lukin JA, Ho C. Chem Rev (Washington, DC, United States) 2004;104:1219–1230. doi: 10.1021/cr940325w. [DOI] [PubMed] [Google Scholar]
- 37.Wiltrout ME, Giovannelli JL, Simplaceanu V, Lukin JA, Ho NT, Ho C. Biochemistry. 2005;44:7207–7217. doi: 10.1021/bi048289a. [DOI] [PubMed] [Google Scholar]
- 38.Gong Q, Simplaceanu V, Lukin JA, Giovannelli JL, Ho NT, Ho C. Biochemistry. 2006;45:5140–5148. doi: 10.1021/bi052424h. [DOI] [PubMed] [Google Scholar]
- 39.Park S-Y, Yokoyama T, Shibayama N, Shiro Y, Tame JRH. J Mol Biol. 2006;360:690–701. doi: 10.1016/j.jmb.2006.05.036. [DOI] [PubMed] [Google Scholar]
- 40.Kavanaugh JS, Rogers PH, Arnone A. Biochemistry. 2005;44:6101–6121. doi: 10.1021/bi047813a. [DOI] [PubMed] [Google Scholar]
- 41.Mueser TC, Rogers PH, Arnone A. Biochemistry. 2000;39:15353–15364. doi: 10.1021/bi0012944. [DOI] [PubMed] [Google Scholar]
- 42.Silva MM, Rogers PH, Arnone A. J Biol Chem. 1992;267:17248–17256. [PubMed] [Google Scholar]
- 43.Noble RW, Hui HL, Kwiatkowski LD, Paily P, DeYoung A, Wierzba A, Colby JE, Bruno S, Mozzarelli A. Biochemistry. 2001;40:12357–12368. doi: 10.1021/bi010988p. [DOI] [PubMed] [Google Scholar]
- 44.Naito A, Hui HL, Noble RW, Hoffman BM. Biochemistry. 2001;40:2060–2065. doi: 10.1021/bi0021028. [DOI] [PubMed] [Google Scholar]
- 45.Naito NR. Chemistry. Northwestern University; Evanston, IL: 1999. [Google Scholar]
- 46.McGourty JL, Peterson-Kennedy SE, Ruo WY, Hoffman BM. Biochemistry. 1987;26:8302–8312. doi: 10.1021/bi00399a042. [DOI] [PubMed] [Google Scholar]
- 47.Miner CS, Dalton NN. Glycerol. Reinhold Pub Corp.; New York: 1953. [Google Scholar]
- 48.Mathlouthi M, Reiser P, editors. Sucrose: Properties and Applications. 1995. [Google Scholar]
- 49.Naito N, Huang H, Sturgess W, Nocek JM, Hoffman BM. J Am Chem Soc. 1998;120:11256–11262. [Google Scholar]
- 50.Page CC, Moser CC, Dutton PL. Curr Opin Chem Biol. 2003;7:551–556. doi: 10.1016/j.cbpa.2003.08.005. [DOI] [PubMed] [Google Scholar]
- 51.Moser CC, Keske JM, Warncke K, Farid RS, Dutton LP. Nature. 1992;355:796–802. doi: 10.1038/355796a0. [DOI] [PubMed] [Google Scholar]
- 52.Lin J, Balabin IA, Beratan DN. Science (Washington, DC, United States) 2005;310:1311–1313. doi: 10.1126/science.1118316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Jones ML, Kurnikov IV, Beratan DN. J Phys Chem A. 2002;106:2002–2006. [Google Scholar]
- 54.Onuchic JN, Beratan DN, Winkler JR, Gray HB. Annu Rev Biophys Biomol Struct. 1992;21:349–377. doi: 10.1146/annurev.bb.21.060192.002025. [DOI] [PubMed] [Google Scholar]
- 55.Beratan DN, Onuchic JN, Winkler JR, Gray HB. Science. 1992;258:1740–1741. doi: 10.1126/science.1334572. [DOI] [PubMed] [Google Scholar]
- 56.Because of the assumption of equivalence, eqs 3 need not include terms for conversion within an ensemble, as they have no physical consequence.
- 57.Steinfeld JI, Francisco JS, Hase WL. Chemical Kinetics and Dynamics. 2. Prentice-Hall, Inc.: Upper Saddle River; New Jersey: 1999. [Google Scholar]
- 58.Schlitter J. Chem Phys. 1988;120:187–197. [Google Scholar]
- 59.Beece D, Bowne SF, Czege J, Eisenstein L, Frauenfelder H, Good D, Marden MC, Marque J, Ormos P, Reinisch L, Yue KT. Photochem Photobiol. 1981;33:517–522. [Google Scholar]
- 60.Ivkovic-Jensen MM, Kostic NM. Biochemistry. 1997;36:8135–8144. doi: 10.1021/bi970327l. [DOI] [PubMed] [Google Scholar]
- 61.Jas GS, Eaton WA, Hofrichter J. J Phys Chem B. 2001;105:261–272. [Google Scholar]
- 62.Davidson VL. Biochemistry. 2000;39:4924–4928. doi: 10.1021/bi992671j. [DOI] [PubMed] [Google Scholar]
- 63.Peterson-Kennedy SE, McGourty JL, Kalweit JA, Hoffman BM. J Am Chem Soc. 1986;108:1739–1746. [Google Scholar]
- 64.Colombo MF, Rau DC, Parsegian VA. Science (Washington, DC, United States) 1992;256:655–659. doi: 10.1126/science.1585178. [DOI] [PubMed] [Google Scholar]
- 65.Parsegian VA, Rand RP, Rau DC. Methods Enzymol. 1995;259:43–94. doi: 10.1016/0076-6879(95)59039-0. [DOI] [PubMed] [Google Scholar]
- 66.Parsegian VA, Rand RP, Rau DC. Proc Natl Acad Sci U S A. 2000;97:3987–3992. doi: 10.1073/pnas.97.8.3987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Natan MJ, Baxter WW, Kuila D, Gingrich DJ, Martin GS, Hoffman BM. Adv Chem Ser. 1991;228:201–213. Electron Transfer Inorg Org Biol Syst. [Google Scholar]
- 68.Roche CJ, Guo F, Friedman JM. J Biol Chem. 2006;281:38757–38768. doi: 10.1074/jbc.M608835200. [DOI] [PubMed] [Google Scholar]
- 69.Courtenay ES, Capp MW, Anderson CF, Record MT., Jr Biochemistry. 2000;39:4455–4471. doi: 10.1021/bi992887l. [DOI] [PubMed] [Google Scholar]
- 70.Furukawa Y, Matsuda F, Ishimori K, Morishima I. J Am Chem Soc. 2002;124:4008–4019. doi: 10.1021/ja0171916. [DOI] [PubMed] [Google Scholar]
- 71.Boehr DD, Dyson HJ, Wright PE. Chem Rev (Washington, DC, United States) 2006;106:3055–3079. doi: 10.1021/cr050312q. [DOI] [PubMed] [Google Scholar]
- 72.Lukin JA, Kontaxis G, Simplaceanu V, Yuan Y, Bax A, Ho C. Proc Nat Acad Sci USA. 2003;100:517–520. doi: 10.1073/pnas.232715799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Fiechtner MD, McLendon G, Bailey MW. Biochem Biophys Res Comm. 1980;96:618–625. doi: 10.1016/0006-291x(80)91400-x. [DOI] [PubMed] [Google Scholar]
- 74.Daugherty MA, Shea MA, Ackers GK. Biochemistry. 1994;33:10345–10357. doi: 10.1021/bi00200a015. [DOI] [PubMed] [Google Scholar]
- 75.Goldbeck RA, Esquerra RM, Kliger DS, Holt JM, Ackers GK. Biochemistry. 2004;43:12065–12080. doi: 10.1021/bi0493923. [DOI] [PubMed] [Google Scholar]
- 76.Goldbeck RA, Esquerra RM, Holt JM, Ackers GK, Kliger DS. Biochemistry. 2004;43:12048–12064. doi: 10.1021/bi049393v. [DOI] [PubMed] [Google Scholar]
- 77.Lalezari I, Lalezari P, Poyart C, Marden M, Kister J, Bohn B, Fermi G, Perutz MF. Biochemistry. 1990;29:1515–1523. doi: 10.1021/bi00458a024. [DOI] [PubMed] [Google Scholar]
- 78.Schay G, Smeller L, Tsuneshige A, Yonetani T, Fidy J. J Biol Chem. 2006;281:25972–25983. doi: 10.1074/jbc.M604216200. [DOI] [PubMed] [Google Scholar]
- 79.Noble RW, DeYoung A, Vitale S, Cerdonio M, DiIorio EE. Biochemistry. 1989;28:5288–5292. doi: 10.1021/bi00438a055. [DOI] [PubMed] [Google Scholar]
- 80.Davydov R, Kofman V, Nocek J, Noble RW, Hui H, Hoffman BM. Biochemistry. 2004;43:6330–6338. doi: 10.1021/bi036273z. [DOI] [PubMed] [Google Scholar]
- 81.Samuni U, Roche CJ, Dantsker D, Juszczak LJ, Friedman JM. Biochemistry. 2006;45:2820–2835. doi: 10.1021/bi050010i. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Pletneva EV, Fulton DB, Kohzuma T, Kostic NM. J Am Chem Soc. 2000;122:1034–1046. [Google Scholar]
- 83.Nocek JM, Stemp EDA, Finnegan MG, Koshy TI, Johnson MK, Margoliash E, Mauk AG, Smith M, Hoffman BM. J Am Chem Soc. 1991;113:6822–6831. [Google Scholar]
- 84.Mei H, Wang K, Peffer N, Weatherly G, Cohen DS, Miller M, Pielak G, Durham B, Millett F. Biochemistry. 1999;38:6846–6854. doi: 10.1021/bi983002t. [DOI] [PubMed] [Google Scholar]
- 85.Feng C, Kedia RV, Hazzard JT, Hurley JK, Tollin G, Enemark JH. Biochemistry. 2002;41:5816–5821. doi: 10.1021/bi016059f. [DOI] [PubMed] [Google Scholar]
- 86.Lasey RC, Liu L, Zang L, Ogawa MY. Biochemistry. 2003;42:3904–3910. doi: 10.1021/bi027055t. [DOI] [PubMed] [Google Scholar]
- 87.Schlarb-Ridley BG, Mi H, Teale WD, Meyer VS, Howe CJ, Bendall DS. Biochemistry. 2005;44:6232–6238. doi: 10.1021/bi047322q. [DOI] [PubMed] [Google Scholar]
- 88.Wang H, Lin S, Allen JP, Williams JC, Blankert S, Laser C, Woodbury NW. Science (Washington, DC, United States) 2007;316:747–750. doi: 10.1126/science.1140030. [DOI] [PubMed] [Google Scholar]
- 89.Ren Y, Wang W-H, Wang Y-H, Case M, Qian W, McLendon G, Huang Z-X. Biochemistry. 2004;43:3527–3536. doi: 10.1021/bi036078k. [DOI] [PubMed] [Google Scholar]
- 90.Hazzard JT, Poulos TL, Tollin G. Biochemistry. 1987;26:2836–2848. doi: 10.1021/bi00384a027. [DOI] [PubMed] [Google Scholar]
- 91.Everest AM, Wallin SA, Stemp EDA, Nocek JM, Mauk AG, Hoffman BM. J Am Chem Soc. 1991;113:4337–4338. [Google Scholar]
- 92.Marshall DB. Anal Chem. 1989;61:660–665. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fits to the simple photocycle of Scheme 1 (Fig S1), solutions to the differential equations for Scheme 2, variation of the RP fit parameters on molality (Fig S2), fits to the KD model generated with the initial parameter set (Fig S3), and modified version of Scheme 2 that incorporates dissociation of the Hb tetramer into dimers, discussion of yields and detectability factors with supporting tables (S1-S3).


