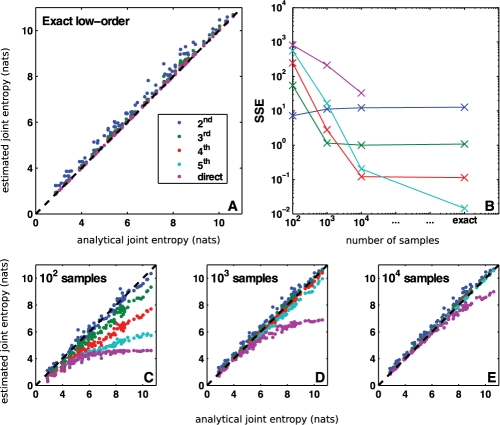
Fig. 1.

Direct validation of MIST entropy approximation. To evaluate the MIST framework, we simulated 100 randomly generated networks with analytically computable joint entropies and applied the metrics using a range of sample sizes. When the analytical entropies are known exactly (A), the higher order approximations perform increasingly well. When the entropies are estimated from a finite sample, however (C–E), the approximations provide the best estimates, with the higher order approximations performing better as more data become available. This behavior is quantified by computing the sum-of-squared error of each metric as a function of the sampling regime (B). The best approximation to use depends upon the amount of data available, but for all cases examined with finite sample size, the approximations outperform direct estimation and the second-order approximation provides a good estimate.