Motor Learning and Consolidation: The Case of Visuomotor Rotation

Abstract

Adaptation to visuomotor rotation is a particular form of motor learning distinct from force-field adaptation, sequence learning, and skill learning. Nevertheless, study of adaptation to visuomotor rotation has yielded a number of findings and principles that are likely of general importance to procedural learning and memory. First, rotation learning is implicit and appears to proceed through reduction in a visual prediction error generated by a forward model, such implicit adaptation occurs even when it is in conflict with an explicit task goal. Second, rotation learning is subject to different forms of interference: retrograde, anterograde through aftereffects, and contextual blocking of retrieval. Third, opposite rotations can be recalled within a short time interval without interference if implicit contextual cues (effector change) rather than explicit cues (color change) are used. Fourth, rotation learning consolidates both over time and with increased initial training (saturation learning).

Introduction

Adaptation is the reduction in systematic errors introduced by altered conditions in order to return to a former level of performance. Conditions can either be internal, for example muscle fatigue, or external, for example looking through a prism. Adaptation, unlike acquiring a new skill, does not require acquisition of a new pattern of muscle activations, i.e., a new capability, but rather of a new mapping between well-learned movements and the spatial goal. For example, if I need to move my arm to the right to make a cursor on a screen go upwards I need to learn the new mapping: up on the screen = right with my arm. However, I have made rightward movements with my arm all my life –there is no need to learn anything new in terms of muscle activations. This is not to say that one cannot become more skilled once in the adapted state, for example in timing the rightward movement of the arm to get the cursor into the target within an imposed time window.

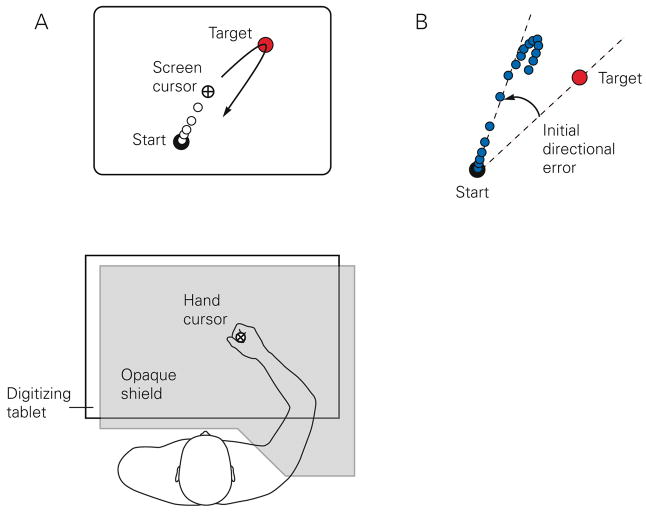
Here we describe a series of experiments, mostly from our laboratory, which examine adaptation to visuomotor rotations and the factors that influence subsequent recall of learning. The choice of this particular transformation stems from the widely accepted view that the nervous system represents and plans reaching movements as a vector in extrinsic space with independent specification of extent and direction (Gordon et al. 1994; Vindras and Viviani 1998; Ghez et al. 2000). Such vectorial planning implies establishment of a scaling factor relating target distance to a peak velocity, and hand-centered reference axes relative to an egocentric reference frame. For movement planning to remain accurate across of a variety of tasks with widely varying spatial characteristics, both operations must be under adaptive control. Visuomotor rotation is a screen-cursor transformation that introduces a systematic directional bias around the hand and thus can be used to probe the adaptive processes underlying planning of reaching direction (Fig. 1, see caption for details) (Krakauer et al. 2000).

Fig. 1.

A. Typical experimental set-up with vision of the arm occluded. B. Directional error seen by a subject when they first are exposed to a 30° CCW rotation; only one target is shown

Although this chapter deals with adaptation to rotation, many of the concepts are applicable to motor learning in general. The term adaptation will be used to describe the actual process of trial-by-trial error reduction while the term learning will be used to describe the state achieved at the end of the adaptation process. This change of state can be probed for both by the presence of after-effects and enhanced rate of adaptation at the time of recall (see below).

Adaptation

We, and others, have shown that error reduction during adaptation to rotations up to 90° in size, proceeds incrementally and exponentially, shows limited generalization, and produces large and prolonged aftereffects (Krakauer et al. 2000; Cunningham 1989; Wigmore et al. 2002; Caithness et al. 2004). After-effects are a strong clue that a new representation has been learned. All these features suggest that adaptation to rotation, in contrast, for example, to learning the chronological order of the kings and queens of England, is an implicit process. A process can be deemed implicit in two different ways. One definition is if the subject is not conscious of the underlying task structure and/or perturbation but nevertheless manages to reduce errors over successive trials (Frensch 1998; Willingham 2001). A second definition considers a process implicit if it is non-intentional and automatic (Frensch 1998). The use of incremental rotations has shown that subjects can adapt whilst unaware that they are making systematic directional errors (Kagerer et al. 1997; Klassen et al. 2005). This result suggests that rotation can be learned purely implicitly but it does not answer the question whether explicit processes can enhance or substitute for implicit rotation learning. There is a precedent for this when it comes to sequence learning, where it has been shown that learning in the serial reaction time (SRT) task, arguably implicit, is enhanced by explicit awareness of sequence elements (Reber and Squire 1994, 1998). The analogous situation had not been addressed for visuomotor adaptation, although it has been proposed that some unexpected results with regard to learning of rotations might be explained by the use of explicit cognitive strategies, for example, the observation of unexpectedly broad generalization with local rotation learning (Imamizu et al. 1995) and the absence of significant after-effects even when substantial adaptation has occurred (Buch et al. 2003).

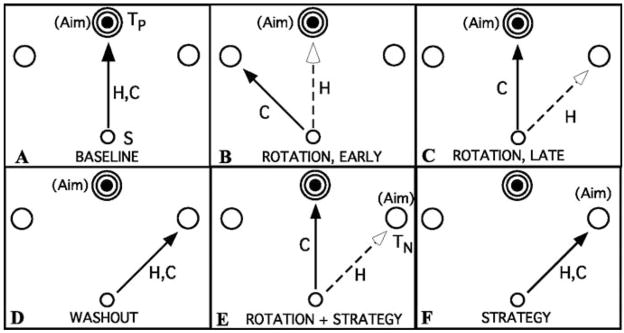
To specifically address the question whether explicit strategies can be used to adapt to a visuomotor rotation, we recently performed an experiment in which subjects were informed of a 45° counter-clockwise (CCW) rotation and given a cognitive strategy to counter it: aim for the target 45° clockwise (CW) from the desired target in order to ensure that the cursor enters the desired target. (Fig. 2, see caption for details). The strategy is shown in 2E, the subject aims for T_N and the cursor will immediately go into T_P because of the imposed CCW rotation (Mazzoni and Krakauer 2006).

Fig. 2.

Task conditions for conscious versus unconscious learning experiment. Each frame shows the start circle (S) and three of eight surrounding targets. The bull’s-eye pattern indicates the target proper (T_p), and the two open circles are the neighboring targets, 45° away. The arrows indicate the direction of hand and cursor movements (H and C, respectively). A, baseline. B, Early rotation (45° CCW). C, Late rotation. D, Washout. E, Rotation plus strategy. F, Strategy only. In A–D, subjects aim for T_p. In E and F, subjects aim for T_n. Taken from Mazzoni and Krakauer, 2006

The prediction was that successful implementation of the strategy would result in an abrupt stepwise cancellation of errors and the absence of aftereffects. Subjects were indeed initially effective in canceling the rotation with errors returning immediately to near zero (beginning of phase III in Fig. 3A). Surprisingly however, as subjects continued to make movements they made increasingly large directional errors, leading the cursor away from the desired target, T_P, and toward the neighboring target, T_N. This can be seen clearly in Fig 3A as worsening directional error as phase III progresses.

Fig. 3.

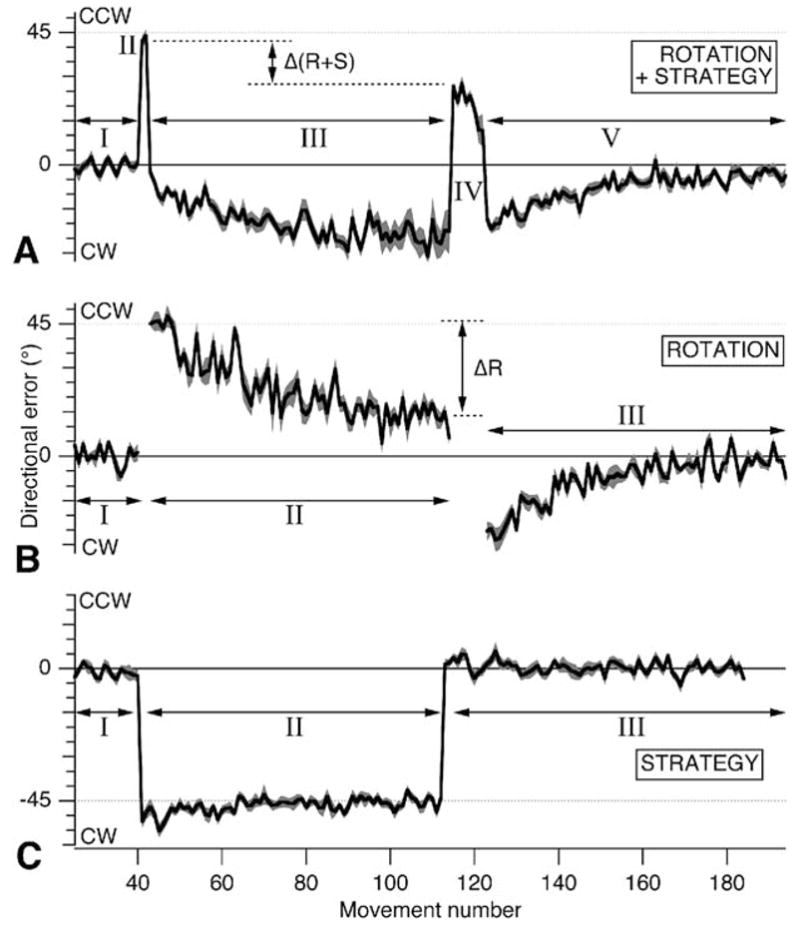
Time course of directional error (mean+/−SE, in degrees) at the endpoint for each group. A, Rotation plus strategy. B, Rotation. C, Strategy. Roman numerals indicate changes in condition or instruction. Taken from Mazzoni and Krakauer, 2006

This suggested that subjects were incrementally adapting to the rotation around T_N at the cost of not fulfilling the task requirement to be accurate to T_P. To demonstrate that subjects indeed adapted implicitly around T_N, we instructed them to stop using a strategy and aim to T_P. This showed an error that was significantly lower than the expected 45° (phase IV in Fig 3A) and strongly suggested that implicit learning of the rotation had occurred. This was confirmed when they were switched back to zero degrees (washout) and showed prolonged aftereffects. An additional finding was that the initial rate of adaptation to T_N was not significantly different from adaptation to the same sized rotation in the absence of a cognitive strategy (Fig. 3B). When subjects were asked about what they thought was happening after the experiment they all expressed frustration at the fact that they became progressively worse at hitting the target and were unaware that they were adapting to the rotation. These results lead to the following conclusions. First, rotation learning is implicit and independent of explicit strategies – it occurs without subject awareness and at the same rate even in the presence of a conflicting cognitive strategy. Second, the motor system will always undergo adaptation when the desired or estimated hand trajectory and the executed trajectory in visual space are incongruous. This suggests the presence of a forward model whose prediction error (the discrepancy between the desired and resultant trajectory) is reduced through adaptation, even at the expense of the explicit task goal.

Savings

In the first section, we provided experimental evidence that strongly supports the notion that rotation learning is an implicit process. In this section, we address implicit memory for rotation learning, and how it influences adaptation on subsequent exposure to the same rotation. Recall of previous rotation learning is apparent as “savings”: adaptation is more rapid and learning more complete when subjects are re-exposed to the same rotation after a time interval that can be as long as a week, if not longer (Krakauer et al. 2005). Thus motor memory is apparent as savings in performance over several trials, which distinguishes it from single-trial declarative memory. There is some confusion in the literature about savings because of a tendency to conflate a reduction in initial absolute error in the first trial with a subsequent increased rate of re-adaptation. The initial absolute error is best thought of as an after-effect, namely that learning carries-over anterograde onto subsequent exposure to the rotation. This is likely to be more significant when there is only a short interval between first and second exposures (minutes). For example for adaptation to a 30° rotation with planar reaching movements, we have seen a contribution of approximately 50% of previous learning on the initial absolute error for the first movement at re-adaptation 5 minutes later. However, this carry over is small after an interval of hours (Krakauer et al. 2005) or even 15 minutes (Miall et al. 2004). This suggests that there is a decay of a memory trace for the rotated state and a return to the default un-rotated state during the time interval.

Initial absolute error and rate of error reduction have been shown to dissociate with inter-limb transfer of rotation learning. Specifically, it has been shown that adaptation begins back at 30° with one arm ten minutes after learning the same rotation with the opposite arm but there is an increase in the rate of error reduction (Wang and Sainburg 2003). We experimentally induced a similar dissociation, but in the same limb, by introduction of “wash-out” trials in the interval between exposures to the same rotation. The term washout is used because after-effects are removed, which ensures that the initial absolute error is the same at the beginning of adaptation and re-adaptation. Nevertheless, there was a clear rate advantage at relearning. This is an example of off-line learning, a form of consolidation defined as a performance improvement that cannot be attributed to simply starting where you left off (Robertson et al. 2004). For sequence learning, off-line learning has been seen as a decrease in initial absolute error (or a reciprocal increase in performance) in the first trial of the second exposure, after an interval, which is significantly different from the last trial of the first exposure (Walker et al. 2003). It was previously thought that off-line learning may not occur for visuomotor adaptation but this is not the case if it is defined in terms of rate rather than initial absolute error.

The observation that savings can occur after full washout is of interest in the light of a recently proposed two-state model of adaptation, which posits the existence of two distinct processes or modules (Smith et al. 2006). One module, the slow module, responds weakly to error but retains information well, whereas the other, the fast module, responds strongly but has poor retention. In this framework, savings is predicted when subjects are brought back to their baseline state through de-adaptation (e.g. adapting to a counter-rotation after adaptation to a rotation) rather than washout. Savings occurs because de-adaptation drives the fast system in the direction of the counter-rotation and then the fast system decays back in the direction of the subsequent rotation, which leads to savings. However, this two-state model predicts no savings when both the fast and slow systems are reset to zero by full washout, which is contrary to the savings observed for rotation after washout (Krakauer et al. 2005). This contradiction suggests the need for a non-linear model for some forms of savings.

Anterograde and Retrograde Interference

Anterograde interference occurs when, in the commonly employed paradigm task A → task B → task A, either task A interferes with task B or task B interferes with re-learning of task A. Interference is apparent as an increase in the initial error and a reduction in the time constant of subsequent adaptation, i.e., the opposite of savings (Miall et al. 2004; Shadmehr and Brashers-Krug 1997). The two-state model, referred to above, predicts a slower rate of adaptation to B or re-adaptation to A, because the slow module is initially biased against the second adaptation. Retrograde interference occurs when task B interferes with initial learning of task A. This interference could occur because memory for task A is erased or cannot be retrieved (Smith et al. 2006). It is not a simple matter to experimentally distinguish between these two putative mechanisms for retrograde interference.

For rotation learning, it has been repeatedly demonstrated that savings is interfered with if a counter-rotation, equal and opposite in magnitude to the rotation, is learned at some time interval after initial rotation learning (Wigmore et al. 2002; Krakauer et al. 1999). Two findings have led to considerable debate about the relative contributions of anterograde and retrograde mechanisms to interference with rotation learning. First, after interference, the initial error and rate of adaptation are often not significantly different on first and second exposures to the original rotation, i.e., savings is prevented but performance is not worse than naï ve (Krakauer et al. 2005; Miall et al. 2004). Second, interference occurs even when the spacing between rotation and counter-rotation is 24 hours (Caithness et al. 2004; Krakauer et al. 2005). The first observation is not consistent with an anterograde mechanism because this should manifest as a larger initial error and/or decreased rate of readaptation. This has led to investigators to conclude that the mechanism is purely retrograde – the counter-rotation erases the memory of the first rotation. However, the second observation is not consistent with retrograde interference because no temporal gradient of susceptibility can be demonstrated, i.e., interference does not decrease as the interval between rotation and counter-rotation increases. Various hypotheses have been offered in attempt to resolve this paradox. Miall and colleagues (Miall et al. 2004) have suggested that interference is only anterograde but that it is not readily apparent because it is offset by learning-to-learn or metalearning. The result from one of their experiments helps to explain their reasoning (Fig. 4).

Fig. 4.

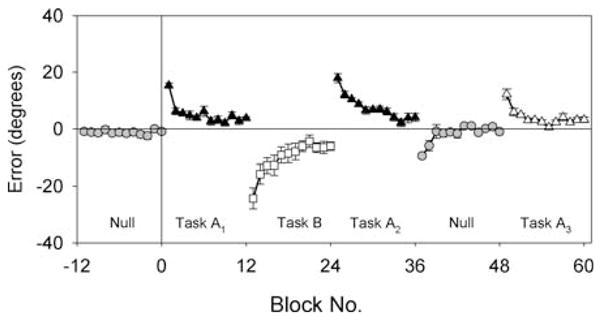
Interference with rotation learning by counter-rotation learning 15 minutes later. Rotation learning shown by progressive reduction in the directional error at peak velocity. Points represent the group cycle average, where each cycle is 16 movements. Null, baseline. Task A1, 30° CCW rotation. Task A2, 30° CW rotation. Task A2, 30° CCW rotation. (Remaining conditions not relevant to current discussion). Taken from Miall et al., 2003 (with permission)

Subjects were made to first learn a 30 CCW rotation (task A1) to a circular array of 8 equally spaced targets presented in random order, and then 15 minutes later they learned a 30° CW counter-rotation (task B). After another 15 minute interval, they re-learned the 30° CCW rotation (task A2). The finding was that the learning curves for the rotation were the same before and after the counter-rotation, both in terms of the average error over the first 16 movements, the rate of subsequent adaptation, and the asymptote achieved. This absence of a difference in performance between A1 and A2 suggests that subjects had no recollection of the first exposure to the rotation. The authors argue, however, that it is erroneous to conclude that interference was retrograde just because performance returned to the naïve state. Their argument stems from the observation that although A1 interfered anterograde with learning of B, B did not in turn interfere anterograde with A2, despite the same 15-minute interval between them. The authors attempt to explain this discrepancy by arguing that it is important to take into account that the magnitude of the directional shift is different the first and second time the rotation is learned. Namely, the first time (baseline to A1), subjects transitioned from an unrotated baseline but the second time (B to A1) they were already rotated by the counter-rotation. Thus when they re-learned the rotation, their initial directional error was the sum of counter-rotated state plus the new 30° CCW rotation (this would be 60°CCW if they had fully learned B). If this “correction” is taken into account, the finding that the rotation is re-learned at the same rate as naïve actually implies savings because subjects started off from a larger directional error but learned just as fast. Thus it only looks like subjects return to the naive state but this appearance is deceptive: it is the net result of the combination of anterograde interference and learning-to-learn; a combination hitherto mistaken for retrograde interference.

This is a provocative argument but there are some problems with it. Namely, the two phenomena, anterograde interference and metalearning, are not demonstrated but surmised. The authors do not show the magnitude of the directional error for the first movement (in the figure, the first point of A2 is the average of the first 16 movements and is no higher than the first block of A1) nor are we shown the rate of learning over this first block. Thus we are not provided with evidence for either anterograde interference (higher initial error at the beginning of A2) or learning-to-learn (higher rate over the first block of A2). It turns out that there was indeed a higher initial error in the first movement and a concomitant increased rate of error reduction in the first 16 movements (personal communication with Chris Miall). However, this still does not explain why the rate advantage, putatively due to metalearning, would appear for the first cycle and then not continue through to subsequent cycles, i.e., why not continue to learn faster in all subsequent blocks instead of just block 1 of A2?

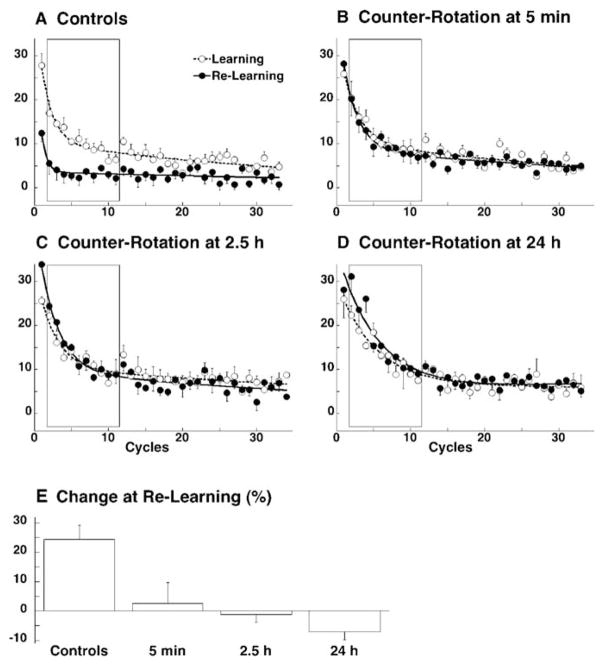
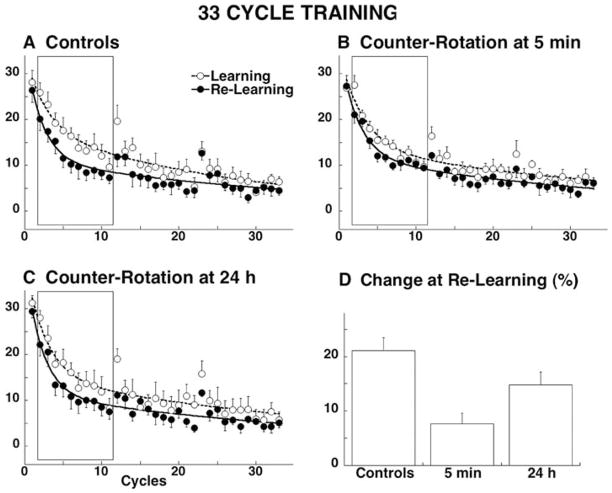
We have in fact corroborated the empirical results obtained by Miall and colleagues. We found that re-learning of a 30° rotation is not significantly different from naïve even when the 30° counter-rotation is learned 24 hours later and relearning tested a week later (see Fig. 5B–D, results summarized in Fig. 5E).

Fig. 5.

Interval-invariant interference with rotation learning by counter-rotation learning. Rotation learning (open circles and dashed lines) and re-learning (filled circles and solid lines) for four separate groups of 6 subjects A–D. Learning is shown by the progressive reduction of the directional error at peak velocity. Points represent the group average with SE for each cycle of eight movements, are fitted with a double exponential function. E. Percent change in error reduction, calculated from cycles 2–11, from learning to re-learning. Taken from Krakauer et al., 2005

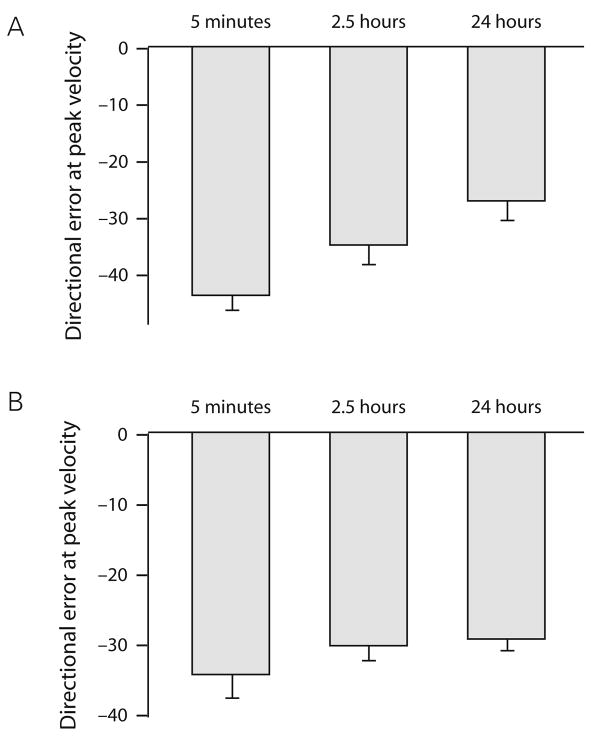
Flanagan and colleagues have also reported similar results (Caithness et al. 2004). To specifically address the possibility that substantial aftereffects carry over from the initial rotation to the counter-rotation we calculated the group mean for the directional error for both the first movement and first cycle of the counter-rotation.

As can be seen in Fig. 6A, there was substantial carry over to the first movement when the counter-rotation was learned 5 minutes after the rotation and only minimal carry over when the counter-rotation was learned 2.5 hours after the rotation. However, when the interval was 24 hours, no anterograde effect was seen. In addition, the mean directional error in the first cycle was not significantly different across the three intervals (Fig 6B). These results therefore support the idea that an aftereffect carries over from rotation to counter-rotation, as suggested by Miall et al. However, this is only true when the interval between rotation and counter-rotation is relatively short because it is gone by 24 hours. Critically however, even though the after-effect decayed after 24 hours, interference by a counter-rotation was just as robust with an interval of one week as it was for an interval of 5 minutes. This is strong proof against the Miall hypothesis, which would predict that learning should be faster in the 24 hour case because now learning-to-learn is no longer going to be cancelled out by an anterograde effect, which has decayed. So where does this leave us? A clue may come from close inspection of the learning curves in Fig. 5B-D, which reveals that for the 3 interference groups, the initial error (first cycle of 8 movements) was consistently higher, albeit only a little higher that 30°, at re-learning compared to day 1 learning. Thus our results do indeed suggest some form of anterograde process, but it does not seem that they are satisfactorily explained by invoking a large virtual aftereffect when only a small aftereffect is in fact observed. We are therefore left with an anterograde interference mechanism that does not operate through aftereffects. We have recently proposed that the mechanism is an inhibitory effect of previous context. The idea here is that there is transient recall of the previous mapping learned in the same context, namely the counter-rotation, but as this mapping is not appropriate it is suppressed. The subtle after effects present, even after a delay of a week, are markers of this transient recall but do not themselves cause anterograde interference. Instead, re-learning of rotation appears naïve because original rotation learning is no longer associated with the task context and so its recall is not triggered. This hypothesis implies that the counter-rotation does not erase the memory of the rotation but rather competes with it for retrieval. A similar phenomenon is described in the declarative memory literature. Specifically, it has been shown that for pair-associates word learning and other forms of episodic memory task (Wixted 2004). In paired-associated word learning, subjects learn an A-B list then, after an interval, they learn an A-C list. If after a short interval they are re-tested on the A-B list, they show impaired retrieval compared to controls who did not learn the intervening A-C list. Impaired A-B retrieval occurs even when the A-C list is learned 24 hours after the A-B list. This process has been called retrieval-induced forgetting (Anderson et al. 1994), whereby the act of recall reduces access to related memories. Interestingly, others have speculated that retrieval-induced forgetting serves to diminish competition between rival memories that share the same retrieval cue (MacLeod and Macrae 2001). We suggest that a very similar process is occurring for visuomotor rotation learning and perhaps for adaptation in general: when two opposite rotations are learned sequentially but in the same experimental context, then the first will be temporarily forgotten. This hypothesis would predict that if the association of the counter-rotation with the context could be reduced then savings and retrograde phenomena might become apparent. This prediction was tested with a series of experiments described in the next section.

Fig. 6.

Decay of after-effects. Bar plots for the mean directional error for A, the first movement and B, the first cycle of the counter-rotation (30° CCW) for groups B–D in Fig. 5

Consolidation as Temporally Graded Resistance to Retrograde Interference

In a series of seminal experiments, Shadmehr and colleagues (Shadmehr and Brashers-Krug 1997; Brashers-Krug et al. 1996) demonstrated that adaptation to a rotatory viscous force field during reaching movements showed savings but that savings was prevented if, after learning the first force field, subjects adapted to a second force field that rotated in the opposite direction. Importantly, these authors found that the second force field no longer interfered with the first if sufficient time, approximately 6 hours, elapsed between the two force fields. These findings showed that motor memory, like declarative memory, undergoes a process of consolidation, whereby one newly acquired internal model becomes increasingly resistant to retrograde interference by a competing internal model simply as a function of time. However, subsequent experiments have failed to show a similar time-dependent resistance to interference for visuomotor adaptation. As outlined in the previous section, we argue that this failure is due to a context effect: there is no cue that allows the subject to distinguish the two internal models and so a recency effect dictates that they recall the last rotation experienced in that context, which is the counter-rotation rather than the original rotation. The one difference is, of course, the clockwise versus counter-clockwise direction of the error itself but this does not seem to be an effective cue when learning a rotation in multiple directions. This is different from vestibular adaptation where the error itself can serve as a contextual cue (Young 2003). Various attempts have been made to overcome this problem by introduction of arbitrary contextual cues that signal the presence of the rotation versus the counter-rotation. For example, displaying a red light for rotation and a blue light for counter-rotation (Miall et al. 2004). However, these attempts essentially fail for reasons that are not entirely clear, although it is perhaps not completely surprising given that there are no direct connections between the visual system and motor areas.

We took a different approach and, rather than using explicit cues, reasoned that if we introduced washout blocks between opposite rotations then subjects would associate the context with the un-rotated baseline state, which would then allow them to call up the appropriate internal model from the two choices available to them rather than being biased in favor of one over the other by a recency effect. The experiment had subjects learn baseline (washout) blocks before any rotation block (Krakauer et al. 2005). This ensured that subjects began without any directional bias before training with rotation. Using this protocol, we found that the counter-rotation led to interference only if it was learned 5 minutes after the rotation but not if it was learned 24 hours later (Fig. 7B,C). Thus, these results were consistent with a consolidation process: the counter-rotation interfered retrograde with the memory of the rotation after 5 minutes because consolidation is interrupted. At 24 hours, consolidation was complete and so interference no longer occurred. However, the situation is not quite as simple as this for two reasons. First, inspection of Fig. 7B shows that there was savings even at 5 minutes but not as much as if the counter-rotation had not been learned. Second, savings at 24 hours were not as great as they would have been in the absence of the washout blocks, compare Fig. 5A with Fig. 7A. Thus, washout blocks succeeded in preventing an anterograde context effect from masking consolidation but also reduced the maximal amount of savings that were observed when there was no washout, , i.e., washout blocks themselves can interfere. This has subsequently been confirmed in a study showing that washout trials can sometimes fully interfere (Hinder et al. 2007).

Fig. 7.

Evidence for retrograde interference and resistance to interference (consolidation) after washout of anterograde effects. Rotation learning (open circles anddashed lines) and re-learning (filled circles andsolid lines) for four separate groups of 6 subjects (A–D). Learning is shown by the progressive reduction of the directional error at peak velocity. Points represent the group average with SE for each cycle of eight movements, are fitted with a double exponential function. E. Percent change in error reduction, calculated from cycles 2–11, from learning to re-learning. Taken from Krakauer et al., (2005)

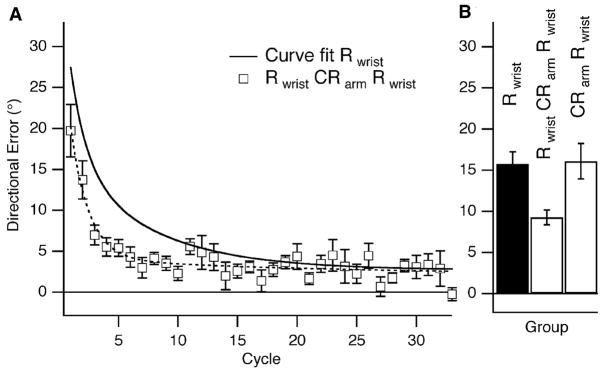
Is there a way to provide a contextual cue to eliminate any interference between two opposite rotations? In a more recent experiment we reasoned that a contextual cue might be more effective if it is implicit rather than explicit (Krakauer et al. 2006 ). We hypothesized that subjects would be able to learn opposite rotations if they were learned using different effectors. Specifically, we had subjects adapt to a 30° CCW rotation with their wrist (shoulder and elbow immobilized) followed 5 minutes later by adaptation to 30° CW rotation with their arm with the wrist immobilized. They then came back 24 hours later and re-adapted to the 30° CCW rotation with their wrist. There was no interference – subjects showed savings of similar magnitude as if they had not had the intervening training with the arm on the counter-rotation (Fig. 8). Thus it appears that implicitly cuing with a change in effectors, presumably mediated through proprioception, can prevent interference between opposite visuomotor maps. This result is consistent with tasks in everyday life, which tend to differ with regard to kinesthetic feedback as well as visual feedback.

Fig. 8.

Evidence for effectiveness of an implicit contextual cue: rotation learning at the wrist (R_wrist) is not interfered with by counter-rotation learning at the arm (CR_arm). A, R_wrist on day 2, after R_wrist followed by CR_arm 5 min later on day 1 (group 7, white squares, dashed curve). There was savings from R_wrist on day 1 to R_wrist on day 2 despite CR_arm. The thick black curve represents R_wrist on day 1 (group 1). B, Bar graph showing a statistically significant difference in the reduction in mean directional error in the first six cycles for R_wrist on day 1 versus day 2 (groups 1 and 7, mean difference = 6.49°, p =0.0036). This difference was absent when only CR_arm was learned on day 1, with no statistically significant difference in the reduction in mean directional error in the first six cycles for day 1 versus day 2 (groups 1 and 8, mean difference = 0.328°, p = 0.88). Taken from (Krakauer et al., 2006)

Consolidation and Saturation Learning

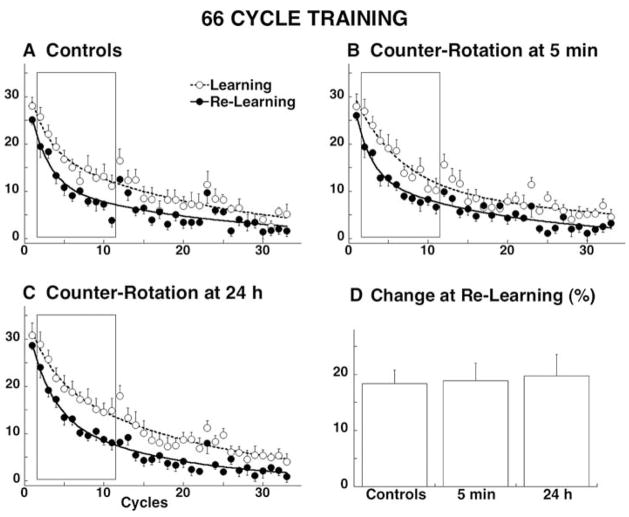
Up until this point, consolidation has been conceptualized as a time-dependent process that occurs between training sessions. However, there is a body of data that suggests that consolidation can be triggered by reaching asymptotic, or saturated, performance within a given training session. For example, in an enumeration task, consolidation, defined as off-line learning rather than resistance to interference, was only seen when subjects’ reaction time reached asymptote within the initial training session (Hauptmann et al. 2005). More relevant to our discussion of rotation learning, is a similar saturation-dependent consolidation effect for prism adaptation. Specifically, the persistence of aftereffects after prism adaptation was investigated in a single monkey (Yin and Kitazawa 2001). The main finding was that when the monkey was trained with 250 trials, there was no significant aftereffect 24 hours later. However, if the monkey was trained for an additional 250 trials (double the amount of training) then aftereffects more than half the size of the original displacement were present three days later. The authors comment: “ This is surprising because the error during the exposure period had already decreased to nil asymptote by the 250th trial. It is the additional repetition of reaching with approximately zero errors that was crucial for triggering the consolidation”.

We made a similar finding in human subjects but consolidation was measured as resistance to interference rather than as persistence of aftereffects (Krakauer et al. 2005 ). We had subjects learn the 30°rotation with washout as described in Consolidation as Temporally Graded Resistance to Retrograde Interference above but trained them with double the amount of trials. Critically, this doubling in the amount of training trials (from 264 to 528) did not lead to a greater degree of adaptation because subjects were already approximately at asymptote after 264 trials. Nevertheless, with this extra training there was no interference by the counter-rotation even after 5 minutes – the same amount of savings were seen at 48 hours with (5 min or 24 h) or without an intervening counter-rotation (Fig. 9A, B, and C). This was true even when the counter-rotation was also trained over 528 trials. Thus, consistent with the prism adaptation after-effects described above, we found that saturation learning within a session led to consolidation of visuomotor rotation learning.

Fig. 9.

Evidence for consolidation by saturation learning. Rotation learning (open circles anddashed lines) and re-learning (filled circles andsolid lines) for four separate groups of 6 subjects A–D. Learning is shown by the progressive reduction of the directional error at peak velocity. Points represent the group average with SE for each cycle of eight movements, are fitted with a double exponential function. E. Percent change in error reduction, calculated from cycles 2–11, from learning to re-learning. Taken from Krakauer et al., 2005

Summary

Adaptation to visuomotor rotations is a specific form of motor learning, distinct from sequence learning, force-field adaptation and skill acquisition. Nevertheless, adaptation to rotation is subject to a number of learning and memory phenomena similar to those seen with these other forms of motor learning and for some declarative memory tasks. This similarity suggests that a somewhat artificial laboratory task is nevertheless able to yield a set of findings with implications for procedural learning and motor memory in general: First, recent data suggests that rotation learning is implicit and proceeds because of a discrepancy between observed and estimated hand trajectory. Implicit learning occurs even when it is contrary to an explicit task goal. Second, experiments show that rotation learning is subject to anterograde and retrograde interference. It is likely that context effects can modulate both types of interference. Third, rotation learning shows between session consolidation both in terms of off-line learning and resistance to retrograde interference. Finally, rotation learning also consolidates within session when performance reaches saturated or asymptotic levels.