Abstract
A key aim in epidemiology is to understand how pathogens spread within their host populations. Central to this is an elucidation of a pathogen's transmission dynamics. Mathematical models have generally assumed that either contact rate between hosts is linearly related to host density (density-dependent) or that contact rate is independent of density (frequency-dependent), but attempts to confirm either these or alternative transmission functions have been rare. Here, we fit infection equations to 6 years of data on cowpox virus infection (a zoonotic pathogen) for 4 natural populations to investigate which of these transmission functions is best supported by the data. We utilize a simple reformulation of the traditional transmission equations that greatly aids the estimation of the relationship between density and host contact rate. Our results provide support for an infection rate that is a saturating function of host density. Moreover, we find strong support for seasonality in both the transmission coefficient and the relationship between host contact rate and host density, probably reflecting seasonal variations in social behavior and/or host susceptibility to infection. We find, too, that the identification of an appropriate loss term is a key component in inferring the transmission mechanism. Our study illustrates how time series data of the host–pathogen dynamics, especially of the number of susceptible individuals, can greatly facilitate the fitting of mechanistic disease models.
Keywords: cowpox, disease, population cycles, Markov chain Monte Carlo
The seminal studies of Anderson and May (1, 2) introduced a framework for modeling the dynamics of pathogens and their hosts that has since underpinned most predictive models of host–pathogen dynamics. It has been standard practice when modeling the dynamics of host–microparasite interactions (viral and bacterial infections) to represent the rate of change of infected hosts I(t) at time t by
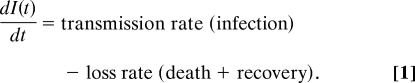 |
However, empirically based identification of appropriate functional forms for the “transmission rate” and “loss rate” terms has not generally been possible for systems with host dynamics because of a lack of sufficient data (although refs. 3 and 4 have recently done this for infectious diseases of human populations).
To date, most studies have used transmission rate terms that are either density-dependent or frequency-dependent (5, 6). The underlying difference between these is the assumption about how host contact rate c, varies with host density [(N(t))/A], where N(t) is host abundance and A, the area occupied by the population, is usually assumed constant and omitted from the equations (6). For density-dependent transmission, host contact rate varies linearly with density [typically adopted for directly transmitted diseases such as measles (7) and foot and mouth disease (8)], whereas for frequency-dependent transmission it is constant [typically adopted for sexually transmitted diseases such as HIV in human populations (9)]. Studies have shown that models parameterized with different transmission terms can predict very different quantitative and qualitative infection dynamics (5, 10, 11), implying that incorrect assumptions about the transmission term could lead to inaccurate predictions.
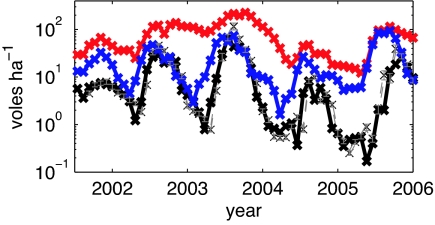
In this study, we use high-resolution time series data on host–microparasite dynamics in wildlife populations to infer whether the most likely transmission term in Eq. 1 is density-dependent or frequency-dependent or is significantly different from either of these. Our dataset comprises 6 years of capture-mark-recapture (CMR) data on the abundance of field voles (Microtus agrestis) sampled every 28 days, for 4 independent populations in Kielder Forest, Northern England. These data have been subdivided into individuals that are susceptible to, infected with, or recovered from cowpox virus (see Methods): a hitherto unprecedented level of information for a wildlife population (Fig. 1 for one site and SI Text, Fig. S1 for all 4 sites). Most individuals in this system become infected with cowpox virus before or soon after reproductive maturity, remain infected for ≈28 days, and thereafter recover and stay immune for life (12, 13).
Fig. 1.
Time series data of cowpox infection status in one natural population of field voles. We show total population size [N(t), red] and the population sizes of susceptible [S(t), blue] and infected [I(t), black] individuals; for brevity, we have omitted the data on recovered individuals. We overlay the mean and 95% credibility intervals of estimated I(t) for our best-fit model (Eq. 5) by using the mean best-fit parameters (q = 0.62, β = 0.18, M = 7.1, Δ = 0.69, A = 0.67, gray). The qualitative patterns are very similar for all four populations studied (see SI Text, Fig. S1).
In common with most host–pathogen interactions, we have very little information about the important physiological, behavioral, and environmental factors that determine how the disease is transmitted in this system. Cowpox is thought to be transmitted only through direct contact (14), implying that the rate of contacts may be a major determinant of the infection dynamics. However, a wide range of factors may affect contact rates in these populations, such as breeding male and female territoriality, movement patterns of subadults, and dispersal that is seasonal- and density-dependent (15–17). As a result, we do not know a priori the appropriate transmission term to use, but it could plausibly incorporate elements of both density- and frequency-dependent transmission. Various transmission relationships have been proposed (5). Here, we focus on the nature of the density dependence in the standard transmission rate function, because relationships varying in this respect have the most transparent biological meaning, and this ties our work to the overriding majority of previous (mainly theoretical) studies. The few empirical studies (18–21), lacking the methodologies developed here and with comparatively few data, have been limited to simple comparisons of density and frequency dependence.
At the end of our study, we also consider the level of support in our data for a seasonal transmission rate, and for seasonality in the density dependence of transmission, in particular. Seasonal transmission seems likely in our study system (and doubtless others) because of the strongly seasonal nature of births, deaths, and dispersal, as well as other behaviors. Seasonal transmission, in general, has received recent (theoretical) attention, in part because of concern over the possible impact of climate change on host–pathogen dynamics and our general lack of understanding of the existence and effects of seasonality in these systems (22).
Derivation of a Generalized Transmission Equation.
To reflect the possibility that transmission may lie between the traditional definitions of density and frequency dependence, we utilize a simple expression for transmission that allows for a spectrum of relationships between host contact rate and abundance:
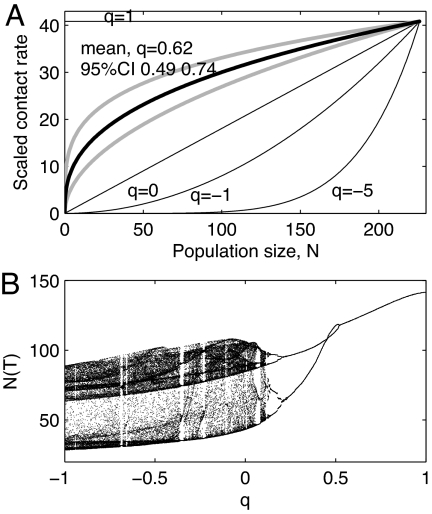
where c is an individual's contact rate (t−1), κ is a species-specific constant (individuals(q−1) t−1), and q is a dimensionless scaling exponent that determines the relative importance of adding an individual to a population for the average contact rate of that population. Fig. 2A illustrates the relationship between contact rate and density for different values of q. Between, and beyond, the special cases of density- and frequency-dependent infection (q = 0 and q = 1, respectively), host contact rate is a nonlinear function of host density. Biologically, this means that q controls the relative importance of changes to the abundance of a population for the average contact rate in that population. In particular, between q = 0 and q = 1, contact rate saturates with increasing population density. This could occur, for example, because of the finite time required for suitable contacts to be made between individuals (23). In contrast, for values of q < 0, contact rate increases with N raised to a power >1, which might occur if the fraction of individuals separated by territoriality decreases with increasing population density.
Fig. 2.
The shape and effects of nonlinear contact rate–abundance relationships. (A) Example realizations of the relationship between contact rate and population size for different values of q in Eq. 2, and the mean and 95% credibility intervals supported by our best model (Eq. 5). The lines have all been scaled to have the same mean value for βqD = κυ/A, which was set equal to the mean value from our best-fit model. (B) Qualitative demonstration of the potential importance of q to the dynamics predicted by our previously published vole-disease model (24). N(T) is the total population size at time T, the start of the reproductive season. See SI Text and Fig. S5 for full details of the model.
Given this formulation, the infection term in Eq. 1 can be expressed as
where S(t) and I(t) are the population sizes of individuals that are susceptible to infection and infected, respectively, and υ (dimensionless) is the proportion of contacts between susceptible and infected individuals that lead to infection (6). Eq. 3 can then be simplified to give the generalized transmission term
where βqD = κυ/A (individuals(q−1) t−1), K is a rescaling constant (individuals) and the rescaled transmission coefficient β = βqD/Kq [(individuals·time)−1]. We want to identify the value of q that best captures the transmission process in the cowpox–field vole system, and in particular, whether it is significantly different from the traditional assumptions of q = 0 and q = 1(with infection rates typically modeled as βqDS(t)I(t) and βqDS(t)I(t)/N(t), respectively). Our new but simple rescaling of β = βqD/Kq addresses the problem that the units of βqD have differed in previous studies depending on whether q = 0 or q = 1 (6). This rescaling makes parameter estimation easier because the units of β (unlike βqD) can be estimated independently of q (although the value of the rescaling parameter K affects the values estimated for β). Moreover, this separation also facilitates our incorporation of seasonality into the transmission function, which can be done by making either, or both, of q and β seasonal.
Illustration of the Effects of Nonlinear Transmission on Host–Disease Dynamics.
To illustrate the importance of evaluating the transmission term for this, and other host–disease systems, we modified a model, which we previously used to investigate the dynamics of plausible rodent–microparasite interactions (24), to incorporate our Eq. 4 as the transmission term (details in SI Text). Previously we had assumed density-dependent transmission and showed that, for parameter combinations appropriate for the cowpox–field vole system, the host–pathogen interactions could lead to multiyear host cycles of 4-year periods, analogous to those seen in the field data. However, for the same parameter values, but with q = 0.5, the model predicts seasonal oscillations that are exactly repeated every 2 years (Fig. 2B), and for q = 1 it predicts the same seasonal oscillation every year. Repeating this study with added stochasticity (details in SI Text and Fig. S5) removes the bifurcation structure apparent in Fig. 2B but illustrates that changes in q alter the dominant period and amplitude of the seasonal oscillations, as well as the average host abundance. This suggests that identifying the nature of the relationship between host contact rate and density may alter the accuracy of predictions of host–disease dynamics in this and presumably in other systems. Note that we include this example for illustration purposes only and that this model has not been fitted to our dataset.
Results
We inferred the relationship between contact rate and population density in our datasets on cowpox–field vole dynamics (Fig. 1 and SI Text and Figs. S2–S4, S6) by using Eq. 1 with Eq. 4 as the transmission rate term. We can fit Eq. 1 alone because we have actual empirical time series for both of the other population components. In addition, we do not yet have population models for the changes through time in susceptible or recovered individuals, or overall abundance, that are supported by field data. To infer Eq. 1 we also had to assume functional forms for the loss rate term. Previous studies have reported data on the recovery rate of field voles after infection by cowpox virus (13) and on the effects of cowpox on field vole survival rate in Kielder Forest (27). We used this information to construct a series of plausible recovery terms and explored which of these was best supported by the data. Specifically, loss rate was represented either as a combined “death plus recovery” term (with or without seasonality in loss rate), or as separate terms in which death rate could be seasonal or constant and recovery rate was a function of the infection rate 28 days previously (representing a fixed 28-day infected period; see Table 1 and Methods).
Table 1.
Comparison of model performance in predicting the abundance of infected individuals over a 28 day interval
| Loss rate term | Loss rate = | Relative mean -log10(likelihood) |
Relative DIC |
||
|---|---|---|---|---|---|
| No site differences | Site differences | No site differences | Site differences | ||
| Seasonal (death + recovery) | M(1+α sin(2π(t−Δ)))I(t) | 0 | −1.6 (−4.4, 1.6) | 0 | 1.3 |
| Constant (death + recovery) | γI(t) | 14 (12, 16) | 12 (10, 15) | 13 | 13 |
| Recovery 28 days, seasonal death | 37 (35, 39) | 36 (33, 39) | 37 | 38 | |
| Recovery 28 days, constant death | 44 (42, 46) | 41 (39, 44) | 44 | 42 | |
M, α, and Δ are the mean, amplitude, and phase shift, respectively. γ is the constant loss rate. τ = t − ε, where the period of infection ε is 28 days. Seasonal loss rate Λ (t) = exp(−∫τt D(x)Δ x), where seasonal mortality is D(t) = b(1 + a sin(2π (t − σ ))), with b, a, and σ being the mean, amplitude, and phase shift, respectively. λ is the constant death rate. 95% credibility intervals for −log10(likelihood) are given in parentheses.
Our tests showed (Table 1) that the following model formulation is best supported by the data:
where loss (death plus recovery) varies seasonally, M is the mean loss rate (t−1), and α (dimensionless) and Δ (time) scale, respectively, are the amplitude and phase of the seasonal oscillation. Thus, a seasonally varying loss rate (death plus recovery) term was strongly supported by our model selection (Table 1, Fig. 3B, and SI Text). A priori selection of an alternative loss term would have resulted in a model with a much poorer fit (Table 1). A comparison between the predicted and observed values of I(t) for this model is shown in Fig. 1 and Fig. S1.
Fig. 3.
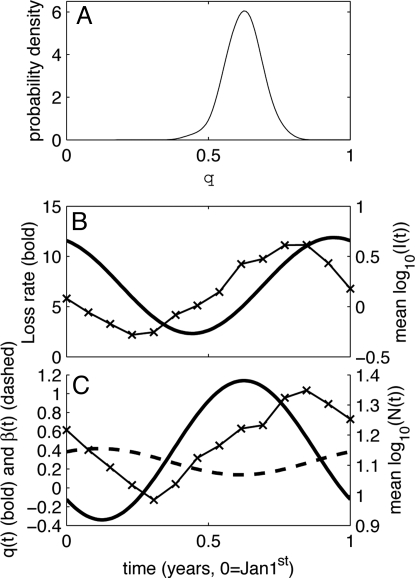
Parameter estimation results for the best-fit model of cowpox infection in field vole populations (Eq. 5). (A) Probability density function for estimated q (see Methods). See Fig. S2 for probability distributions of the other parameters. (B) Example realization of the best-fit seasonal loss rate (M = 7.1, Δ = 0.69, A = 0.67), with the time series data of infected population density overlaid [taking mean of log10(I(t)) of the four sites and for the four complete years of time series data]. (C) Example results of making the parameters q and β functions of time when fitting Eq. 5 to the data, alongside the mean annual variation in log10(total vole density), averaged across all sites.
Most importantly, our analyses support a transmission term that lies between density- and frequency-dependent transmission, with a mean value of q = 0.62 and 95% credibility intervals of 0.49 and 0.74. These analyses unanimously reject q = 0 and q = 1 as credible values (Fig. 3A). Repeating our fitting methodology with this model, but with either q = 0 or q = 1 results in models that are significantly worse in terms of both likelihood (relative mean log10 likelihoods of 12.2 and 6.33, respectively) and Deviance Information Criterion (DIC) values (28) (relative DIC of 12.5 and 6.16, respectively).
We also investigated the extent to which our best-fit parameters were consistent across the 4 replicate sites, to allow us to assess the consistency and generality of our results (see Methods). Accounting for site differences in the parameters does improve the model fit to the data, as expected (Table 1). However, these site-specific differences in parameter values are not dramatically different from those estimated when site differences were ignored (see SI Text and Figs. S2–S4, S6), and the DIC values do not support the increased number of parameters (Table 1). This indicates that our best-fitting model supports infection dynamics that are consistent across all sites.
We extended our study to investigate whether seasonality in the transmission function in Eq. 5 would improve the model fit to the data. Specifically, we investigated whether incorporating a seasonal transmission coefficient β, or seasonal variation in the density dependence of host contact rate q, significantly improved the model predictions. To do this we replaced these constant parameters with parameters that could vary sinusoidally over a year and estimated the best supported parameters by using the same methodology as before. Incorporating seasonality in both parameters was supported (see SI Text for details). We found that the greatest improvement in fit was made by allowing both β and q to vary seasonally (increasing mean log10 likelihood by 9.9) and, of the individual terms, allowing q to vary seasonally resulted in the largest improvement in fit (increasing mean log10 likelihood by 7.8 compared with 4.18). Both models that allowed q to vary supported a strongly seasonal oscillation with a minimum in winter and a maximum in summer (Fig. 3C). This implies transmission that is close to being density-dependent in winter, close to being frequency-dependent in summer, and for most of the year, varies between these two extremes. In contrast, the models supported seasonal variation in β that is almost exactly out of phase with that in q. When combined, these seasonal terms suggest a transmission rate that peaks in summer and has a trough in winter.
Discussion
Our main finding is that our best-fit models generally support a transmission function that lies between the traditional assumptions of true density- and frequency-dependent transmission. These results therefore contrast with, but cannot contradict, previous attempts to infer a transmission function for cowpox virus infection in wild rodents (18, 19), because these simply compared density and frequency dependence (with results tending to support the latter). The key contrasts between the present study and those done previously are the improved quality and quantity of data and the improved methodology for estimating parameter values and functional forms.
The value of q = 0.62 in our best-fit model without seasonal transmission means that contact rate increases with density at low densities but tends to saturate as density increases further (Fig. 2A). Such nonlinearity is consistent with a variety of plausible (but currently unproven) biological mechanisms, such as heterogeneity in the host–contact network (29), the limiting time available for contacts to be made (23), or simply changes in the behavior of individuals with population density (17). However, regardless of the underlying cause, we have shown (Fig. 2B) that the nonlinear nature of this relationship can lead to dynamics that are different from those predicted by density- or frequency-dependent transmission.
We explored the effects of fitting a variety of seasonal loss terms that, for simplicity, ignored the likelihood that there is a minimum infection period before recovery, beyond which there is variation in the time taken to recover (12, 13). This leads us to expect that the average per capita recovery rate will be low when the infected population is made up of a greater proportion of newly infected individuals (when the infected subpopulation is growing fastest) and will be high when it is mostly made up of individuals that have been infected for a relatively long period (when the infected subpopulation is shrinking fastest). This is indeed consistent with the pattern observed in our best-fit seasonal loss term in Eq. 5 (Fig. 3B), which has a trough and a peak that coincide, respectively, with the times of the year when the size of the infected subpopulation is growing or shrinking fastest.
Our analyses also provide support for seasonality in transmission rates. This appears to be the first time field data have provided evidence either for seasonal variation in the density dependence of the transmission rate or for independent variation in the components of transmission, although seasonal variation in the transmission coefficient, β, has been widely supported (4, 19, 22). The seasonal variation in q, with transmission more density-dependent in late winter and more frequency-dependent in late summer, may plausibly be related to seasonal changes in the voles' social structure (15, 29). Established territories in late summer would tend to focus contacts within the relatively fixed number of territory-holding neighbors, whereas the comparative absence of territories in late winter would promote more widespread contact throughout the population. The seasonal variation in β, with transmission rates highest in winter and lowest in summer, may be related to variations in susceptibility, because this pattern matches closely that found recently in these same populations in immunological investment (lymphocyte counts): lowest in winter, highest in late summer (30).
Our methodology to test the relative predictive abilities of the different models uses one-step-ahead prediction, because that time window is a natural timescale for predicting changes in the dynamics of cowpox in field voles (recovery rate is ≈28 days). In terms of predicting 28 days into the future, our best mechanistic models improve substantially on statistical approaches to predicting cowpox prevalence. For instance, linear regression of observed log(I(t)) on predicted log(I(t)) indicates that Eq. 5 explains 67% of the variation in observed log(I(t)) across all datasets (69% with seasonal β and q terms). In comparison, the monthly average explains 35%, a consensus best-fit autoregressive function (with a 28-day time lag) explains 58%, and the best consensus transfer function (equation 6 in ref. 31) explains 56%.
We have also performed a preliminary analysis of the performance of the best-fit model (Eq. 5) over long-term simulations (details in the SI Text and Figs. S7–S8). The model performs well (and better than with q = 0 or q = 1) at simulating the dynamics over a complete 6-year window when using data values for S(t) and R(t) throughout the simulation and initializing with I(0). If, moreover, we discard the observed population dynamics and replace them with a previously published theoretical model (24), while retaining the transmission and loss terms from the best-fit model, long-term simulations still succeed in capturing the qualitative dynamics of seasonal oscillations, although they inevitably fail to recreate the multiyear cycles apparent in the data. This highlights one of the main advantages of having time series of all components of the host–pathogen interaction: it allows us to focus on estimating the infection equation alone without (yet) considering the dynamics of total host abundance (which is often more complex than in human populations; see ref. 36).
In conclusion, possessing high-resolution time series data on the host–pathogen dynamics of our system has enabled us to gain insight into the transmission mechanisms; the nature of density dependence in contact rates most likely lies (or varies) between the traditional assumptions. We hope our study will stimulate future investigations to elucidate more precisely these mechanisms, given their potential importance for accurate predictions of disease dynamics in human, livestock, wildlife, plant, and other populations.
Methods
Inference of Time Series from Capture-Mark-Recapture Data.
Populations were trapped in “primary” sessions every 28 days from March to November, and every 56 days from November to March. Each site had a permanent 0.3-ha live-trapping grid consisting of 100 Ugglan Special Mousetraps (Grahnab) set at 5-m intervals. Individual animals were identified by using s.c. microchip transponders (AVID) injected under the skin at the back of the neck. A 20- to 30-μL blood sample was taken from the tail tip of each individual each primary session. Antibody to cowpox virus was detected in sera by immunofluorescence (IF) assay (32), allowing individuals in each primary session to be classified as seropositive (antibody present) or seronegative. Time series of serological results were used to calculate probabilities that individual animals were infected with cowpox virus (P(I)), were still susceptible (P(S)), or had recovered and were resistant (P(R)) for each trapping session. These were used to subdivide the total population into I, S, and R individuals. The total population size was estimated in program MARK by using Huggins's closed capture model within a robust design (31). For further details, see refs. 27 and 31.
Parameter Estimation and Model Selection.
This methodology is to identify the parameter values in Eq. 1 that most accurately predict the change in abundance of infected individuals, from a known initial state to a state 28 days into the future, for all of the 28-day periods in our 4 independent time series. We chose this one-step-ahead prediction methodology to match the natural timescale of the dynamics of the disease. Our parameter estimation procedure was conducted by using MATLAB and the codes are available from the corresponding author on request.
The Markov Chain Monte Carlo procedure starts with arbitrary values for each parameter. We then use a standard numerical integration algorithm [the MATLAB algorithm “ode45,” which is based on an explicit Runge–Kutta (4,5) formula] to solve our chosen equation over each 28-day time window in our datasets, using these parameter values, and initializing the population size of infected individuals, I(t0), by using the time series. Solution of this equation also requires values for the population densities of susceptible individuals and the total population size, and we used a numerical interpolation algorithm on the time series of S(t) and R(t) (the MATLAB algorithm “interp1,” a 1-dimensional data interpolation, with the “spline” interpolation method chosen). For all analyses we set the scaling constant, K = 226, the maximum population size present in all of our time series.
We evaluate the likelihood of the estimated I(t) values given the observed I(t) values by using the log normal likelihood equation; this assumes log normally distributed process error. Taking the product over observations gives the overall likelihood function for the data given the model. Note that this model assumes no observation error. Simulations that contained both process and observation error were used to assess the validity of this assumption. We found that the methodology was robust to violations of the assumption of no observation error (see SI Text and Table S1 for details), thus obviating the need for a more sophisticated approach of fitting a model with both types of noise (33, 34). Further studies are needed to assess the robustness of our findings to more realistic stochasticity and observation error (36).
The routine then proposes new parameter values by using a random scan approach with Gaussian proposal distributions, with proposals accepted according to the Metropolis–Hastings algorithm (35). The mutation size for the above procedure is chosen such that the average acceptance rate of proposed changes to that parameter was ≈25% [a theoretical optimum (35)]. Parameter proposals outside the biologically plausible ranges result in automatic rejection of the parameters. The number of iterations is chosen such that each parameter value has changes proposed on average 4,000 times in the asymptotic dataset. This results in a sample sufficiently close to the desired likelihood function to give us confidence in the final parameter distributions and to allow model comparisons. All Markov Chain Monte Carlo runs were repeated with different initial conditions to check for convergence.
To account for site-specific parameter differences, we assumed that for each parameter value there exists a site-independent mean and a site-specific deviation from that mean. This gives one global mean and 4 site-specific deviations for each parameter value in our dataset. We modified our parameter mutation algorithm such that every time a site-specific deviation was changed, the change was balanced by changing each of the other site-specific deviations by one-third of that amount and in the opposite direction. This ensures that the average of the site-specific perturbations is equal to zero (or the average of mean plus site-specific deviation for the 4 sites equals the mean).
Supplementary Material
Acknowledgments.
We thank Jonathan Sherratt, Andy White, Steve Paterson, Drew Purves, Jane Rees, Neil Ferguson, Andy Fenton, David Lusseau, Greg McInerny, Anna Renwick, 2 anonymous referees, and the editor for advice that improved the manuscript, and Roslyn Anderson, Pablo Beldomenico, Gemma Chaloner, Stephanie Gebert, Lucasz Lukomski, Matthew Oliver, Jenny Rogers, Andrew Smith, Gill Telford, and David Tidhar for time spent collecting data. This work was supported by Wellcome Trust Grant 075202/Z/04/Z, Natural Environment Research Council, Engineering and Physical Sciences Research Council, Academy of Finland Grant 126364, and Microsoft Research.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. B.G. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/cgi/content/full/0809145106/DCSupplemental.
References
- 1.Anderson RM, May RM. Population biology of infectious diseases. Part I. Nature. 1979;280:361–367. doi: 10.1038/280361a0. [DOI] [PubMed] [Google Scholar]
- 2.May RM, Anderson RM. Population biology of infectious diseases. Part II. Nature. 1979;280:455–461. doi: 10.1038/280455a0. [DOI] [PubMed] [Google Scholar]
- 3.Ferrari MJ, et al. The dynamics of measles in sub-Saharan Africa. Nature. 2008;451:679–684. doi: 10.1038/nature06509. [DOI] [PubMed] [Google Scholar]
- 4.King AA, Ionides EL, Pascual M, Bouma MJ. Inapparent infections and cholera dynamics. Nature. 2008;454:877–880. doi: 10.1038/nature07084. [DOI] [PubMed] [Google Scholar]
- 5.McCallum H, Barlow N, Hone J. How should pathogen transmission be modelled? Trends Ecol Evol. 2001;16:295–300. doi: 10.1016/s0169-5347(01)02144-9. [DOI] [PubMed] [Google Scholar]
- 6.Begon M, et al. A clarification of transmission terms in host-microparasite models: Numbers densities and areas. Epidemiol Infect. 2002;129:147–153. doi: 10.1017/s0950268802007148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Earn DJD, Rohani P, Bolker BM, Grenfell BT. A simple model for complex dynamical transitions in epidemics. Science. 2000;287:667–670. doi: 10.1126/science.287.5453.667. [DOI] [PubMed] [Google Scholar]
- 8.Tildesley MJ, et al. Optimal reactive vaccination strategies for a foot-and-mouth outbreak in the UK. Nature. 2006;440:83–86. doi: 10.1038/nature04324. [DOI] [PubMed] [Google Scholar]
- 9.May RM, Anderson RM. Transmission dynamics of HIV infection. Nature. 1987;326:137–142. doi: 10.1038/326137a0. [DOI] [PubMed] [Google Scholar]
- 10.Truscott J, et al. Control of a highly pathogenic H5N1 avian influenza outbreak in the GB poultry flock. Proc Biol Sci. 2007;274:2287–2295. doi: 10.1098/rspb.2007.0542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hochberg ME. Non-linear transmission rates and the dynamics of infectious diseases. J Theor Biol. 1991;153:301–321. doi: 10.1016/s0022-5193(05)80572-7. [DOI] [PubMed] [Google Scholar]
- 12.Burthe S, et al. Cowpox virus infection in natural field vole Microtus agrestis populations: Delayed density-dependence and individual risk. J Anim Ecol. 2006;75:1416–1425. doi: 10.1111/j.1365-2656.2006.01166.x. [DOI] [PubMed] [Google Scholar]
- 13.Blasdell K. Liverpool, UK: University of Liverpool; 2006. Studies on lymphocytic choriomeningitis virus and cowpox virus in the natural rodent hosts. Ph.D. thesis. [Google Scholar]
- 14.Robinson AJ, Kerr PJ. In: Infectious Diseases of Wild Mammals. Williams ES, Barker I, editors. Ames, IA: Iowa State Univ Press; 2001. pp. 179–201. [Google Scholar]
- 15.Pusenius J, Viitala J. (1993) Varying spacing behaviour of breeding field voles, Microtus agrestis. Ann Zool Fenn. 1993;30:143–152. [Google Scholar]
- 16.Loughran MFE. Social organisation of female field voles Microtus agrestis in a population in Southern England. Acta Theriol. 2006;51:233–242. [Google Scholar]
- 17.Sandell M, Agrell J, Erling S, Nelson J. Natal dispersal in relation to population density and sex ratio in the field vole, Microtus agrestis. Oecologia. 1990;83:145–149. doi: 10.1007/BF00317745. [DOI] [PubMed] [Google Scholar]
- 18.Begon M, et al. Population and transmission dynamics of cowpox in bank voles: Testing fundamental assumptions. Ecol Lett. 1998;1:82–86. [Google Scholar]
- 19.Begon M, et al. Transmission dynamics of a zoonotic pathogen within and between wildlife host species. Proc Biol Sci. 1999;266:1–7. doi: 10.1098/rspb.1999.0870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ryder JJ, Webberley KM, Boots M, White A. Measuring the transmission dynamics of a sexually transmitted disease. Proc Natl Acad Sci USA. 2005;42:15140–15143. doi: 10.1073/pnas.0505139102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Thrall PH, Jarosz AM. Host-pathogen dynamics in experimental populations of Silene alba and Ustilago violacea. II Experimental rests of theoretical models. J Ecol. 1994;82:561–570. [Google Scholar]
- 22.Altizer S, et al. Seasonality and the dynamics of infectious diseases. Ecol Lett. 2006;9:467–484. doi: 10.1111/j.1461-0248.2005.00879.x. [DOI] [PubMed] [Google Scholar]
- 23.Antonovics J, Iwasa Y, Hassell MP. A general model of parasitoid, venereal, and vector-based transmission processes. Am Nat. 1995;145:661–675. [Google Scholar]
- 24.Smith M, et al. Disease effects on reproduction can cause population cycles in seasonal environments. J Anim Ecol. 2008;77:378–389. doi: 10.1111/j.1365-2656.2007.01328.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Clark JS, Bjørnstad ON. Population time series: Process variability, observation errors, missing values, lags and hidden states. Ecology. 2004;85:3140–3150. [Google Scholar]
- 26.Knell RJ, Begon M, Thompson DJ. Transmission dynamics of Bacillus thuringiensis infecting Plodia interpunctella: A test of the mass action assumption with an insect pathogen. Proc Biol Sci. 1996;263:75–81. doi: 10.1098/rspb.1996.0013. [DOI] [PubMed] [Google Scholar]
- 27.Telfer S, et al. The effects of cowpox virus on survival in natural rodent populations: Increases and decreases. J Anim Ecol. 2002;71:558–568. [Google Scholar]
- 28.Spiegelhalter DJ, Best NG, Carlin BP, van der Linde A. Bayesian measures of model complexity and fit (with discussion) J R Stat Soc B. 2002;64:583–639. [Google Scholar]
- 29.Meyers LA, Pourbohloul B, Newman MEJ, Skrowronski DM, Brunham RC. Network theory and SARS: Predicting outbreak diversity. J Theor Biol. 2005;232:71–81. doi: 10.1016/j.jtbi.2004.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Beldomenico PM, et al. The dynamics of health in wild field vole populations: A haematological perspective. J Anim Ecol. 2008;77:984–997. doi: 10.1111/j.1365-2656.2008.01413.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Begon M, et al. Effects of abundance on infection in natural populations: Field voles and cowpox virus. Epidemics. 2009;1:35–46. doi: 10.1016/j.epidem.2008.10.001. [DOI] [PubMed] [Google Scholar]
- 32.Crouch AC, Baxby D, MacCracken CM, Gaskell RM, Bennett M. Serological evidence for the reservoir hosts of cowpox virus in British wildlife. Epidemiol Infect. 1995;115:185–191. doi: 10.1017/s0950268800058258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Buckland ST, Newman KB, Fernández C, Thomas L, Harwood J. Embedding population dynamics models in inference. Stat Sci. 2007;22:4458. [Google Scholar]
- 34.Newman KB, Buckland ST, Lindley ST, Thomas L, Fernández C. Hidden process models for animal population dynamics. Ecol Appl. 2006;16:7486. doi: 10.1890/04-0592. [DOI] [PubMed] [Google Scholar]
- 35.Gilks WR, Richardson S, Spiegelhalter DJ. Markov Chain Monte Carlo in Practice. London: Chapman & Hall; 1996. [Google Scholar]
- 36.Glass K, Xia Y, Grenfell BT. Interpreting time-series analyses for continuous-time biological models-measles as a case study. J Theor Biol. 2003;223:19–25. doi: 10.1016/s0022-5193(03)00031-6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.