Abstract
A given outcome of radiotherapy treatment can be modeled by analyzing its correlation with a combination of dosimetric, physiological, biological, and clinical factors, through a logistic regression fit of a large patient population. The quality of the fit is measured by the combination of the predictive power of this particular set of factors and the statistical significance of the individual factors in the model. We developed a genetic algorithm (GA), in which a small sample of all the possible combinations of variables are fitted to the patient data. New models are derived from the best models, through crossover and mutation operations, and are in turn fitted. The process is repeated until the sample converges to the combination of factors that best predicts the outcome. The GA was tested on a data set that investigated the incidence of lung injury in NSCLC patients treated with 3DCRT. The GA identified a model with two variables as the best predictor of radiation pneumonitis: the V30 (p=0.048) and the ongoing use of tobacco at the time of referral (p=0.074). This two-variable model was confirmed as the best model by analyzing all possible combinations of factors. In conclusion, genetic algorithms provide a reliable and fast way to select significant factors in logistic regression analysis of large clinical studies.
Keywords: genetic algorithm, logistic regression, radiobiological modeling, variable selection
INTRODUCTION
Radiotherapy treatment plans are often evaluated based on dose-volume histograms (DVH) generated from the dose distribution in the target and the surrounding organs at risk (OARs). Many studies have extracted information from DVHs about cell killing in the target and injury of functional subunits in OARs based on radiobiological models.1, 2, 3 Several tools were developed to allow the evaluation of these radiobiological predictors, such as BIOPLAN4 and TCP_NTCP_CALC.5 However, in addition to DVH data, there are other clinical, physiological, and biological factors, such as age or gender of the patient, presence or absence of chemotherapy or surgery treatment, tobacco history, etc. that affect the outcome of radiotherapy (RT) treatment. A more integrated approach of treatment plan evaluation that includes all these factors has recently sparked a growing interest in the radiotherapy community, creating a need for the development of robust data mining and correlation analysis methods. Software tools were developed to address this issue, using, for example, self-organizing maps,6 support vector machine algorithms,7 neural networks,8 or decision trees.9 Two of these tools, DREES10 and EUCLID,11 which are MATLAB-based programs (The MathWorks Inc., Natick, MA), use a logistic regression model to correlate treatment outcomes with clinical factors. A key element in building such a model is the ability to select the variables that yield a high predictive power and statistically significant correlations between clinical factors and outcome. In DREES, the variable selection is performed using sequential forward selection, and the robustness of the model is verified using cross-validation (CV) techniques such as the bootstrap test and the leave-one-out (LOO) method.12
An alternative approach to the variable selection problem is via the utilization of a genetic algorithm.13, 14 Genetic algorithms (GAs) are numerical optimization algorithms inspired by both natural selection and natural genetics. The method is a general one that can be applied to an extremely wide range of problems. The algorithms are usually simple and easy to implement. However the technique never attracted the attention that, for example, artificial neural networks have. The idea of using a population of solutions to solve practical engineering optimization problems was considered several times in the 1950s, but the GA was not invented in essence until the 1960s. Genetic algorithms now have many applications in a wide variety of domains, such as image processing, prediction of three-dimensional protein structures, laser technology, spacecraft trajectories, solid state physics, robotics, building designs, or facial recognition.15 In medicine, this method was demonstrated in the case of logistic regression with an example in the domain of myocardial infarction.16 The authors used a fitness function that rewarded predictive power using the area underneath the receiving-operator characteristic (ROC) curve,17 and parsimonious models through a weight that limits the number of variables to use in the regression. They tested their algorithm on a data set correlating the occurrence of myocardial infarction with a set of 43 clinical variables, and found that the genetic method produced a 16-variable model with a higher predictive power than sequential forward, backward, and composite methods.
In this work, we developed a genetic algorithm to perform variable selection for logistic regression in EUCLID. We used a fitness function that rewards overall predictive power of the model and statistical significance of the selected variables. As an example, the algorithm was tested on a data set from a prospective clinical study aimed at understanding RT-induced lung injury in patients with nonsmall cell lung cancer (NSCLC) treated with three-dimensional conformal radiotherapy (3DCRT).18, 19 We compared our approach to a “brute force” method that calculated all possible combinations of variables to extract the actual optimal model. We also compared our results with those obtained using sequential forward selection.
METHODS AND MATERIALS
Logistic regression
Logistic regression models are commonly used in the field of radiotherapy, where the outcome is often a binary variable: the tumor is controlled, or it is not; there is a development of a complication, or there is not. In this case, the probability P of a treatment outcome Y is derived as a function of the following combination of clinical parameters X={x1,x2,…,xn}:
| (1) |
or
| (2) |
where b={b1,b2,…,bn} are the regression coefficients.20 A nonzero regression coefficient bi represents a correlation between the variable xi and the outcome Y. The regression coefficients and their standard deviations σ are calculated using a least-squares fit, and their statistical significance is determined by the p-value using the Wald test based on the t-distribution, t=b∕σ.
Genetic algorithm
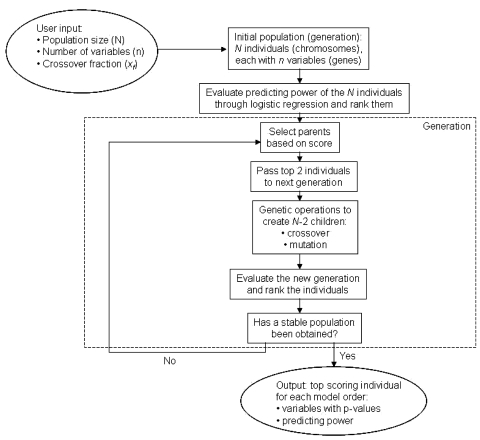
A genetic algorithm (GA) is a heuristic for function optimization where the extrema of the function cannot be established analytically.16 The general principle of a genetic algorithm is summarized in Fig. 1. For the purpose of selecting variables for a logistic regression, a large number of models, i.e., a large number of combinations of clinical factors and DVH parameters, is used to compute a large number of fits to the patient dataset. Each one of these combinations of variables is called an “individual”. The set of individuals forms a “population,” which is not the patient population to be fitted, but rather a set of models to fit to that patient population. Each variable in the combination is called a “gene”. These genes are parameters in the optimization, or fitness, function. The value of the gene is an integer number identifying a variable, or clinical factor. An initial population, composed of a large number of individuals, is randomly created. For each individual, the fitness function is calculated by building a logistic regression model containing the variables in the individual, and the individuals are ranked according to their fitness score, i.e., the ability of that particular set of variables to predict the outcome. The individuals with the highest score are more likely to be selected to become “parents,” ensuring “survival of the fittest,” and two types of genetic operations are performed on them to produce “offspring”: either crossover, where the genes from two individuals are mixed together, or mutation, when a certain number of genes in a parent randomly take another value. The process is repeated over several “generations,” until the population converges towards an optimal set of variables for the logistic regression model.
Figure 1.
Schematic for genetic algorithm, showing the initialization process, the building of the subsequent generations with genetic operations, the evaluation of the population, and the output of the algorithm.
Initialization
The genetic algorithm in EUCLID was adapted from the MATLAB Genetic Algorithm and Direct Search toolbox. A certain number of input parameters need to be defined, including the model order n, i.e., the number of variables to be included in the logistic regression analysis, and the population size N. Each of these N individuals is a combination of n variables, randomly chosen from the full list of available variables defined in the clinical study. If m different model orders are to be investigated, the GA runs m times and m outputs are generated, allowing for the comparison of different model orders.
The fitness function
The fitness function contains two terms, one that rewards the overall predictive ability of the model and one that rewards statistical significance of the variables included in the model. For each individual, a logistic regression model is first built from a large sample of patients to fit the outcome with the set of variables identified in the individual. Two predictive power criteria were tested: the area under the ROC curve (AUC), and the Spearman rank correlation coefficient. The receiving operator characteristic curve is a measure of sensitivity vs. specificity of the model. For a given threshold between 0 and 1, the sensitivity is measured by the true positive rate, that is the fraction of events for which the model calculates a probability, according to Eq. 2, higher than the threshold, and the observed outcome is positive. The value of (1-specificity) is measured by the false positive rate, that is the fraction of events for which the model calculates a probability higher than the threshold, and the observed outcome is negative. For the construction of the curve, the values of sensitivity and (1-specificity) are plotted on the vertical and horizontal axis, respectively, for different threshold values between 0 and 1 in steps of 0.1. The area under that curve is 1 for a model that perfectly predicts the observed outcome, 0.5 for a model that is no better than a coin toss, and 0 for a model that always predicts the opposite outcome. The other predictive power criterion that was tested was the Spearman rank correlation coefficient, which measures the correlation between the distribution of ranks of the probabilities calculated by the model, according to Eq. 2, and the distribution of ranks of observed outcomes. The Spearman rank correlation coefficient is 1 for a model that perfectly predicts the observed outcome, 0 for a model that is no better than a coin toss, and −1 for a model that always predicts the opposite outcome.
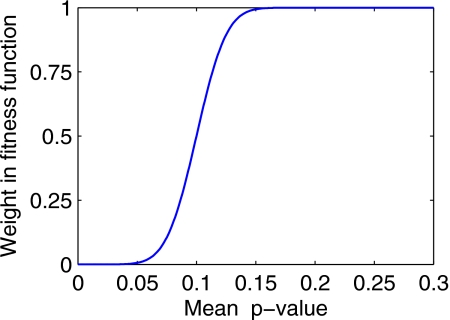
The second term of the fitness function is a function of the p-values of the regression coefficients. The goal is to penalize models that include clinical factors whose correlation with the outcome is not statistically significant, i.e., for whom the p-value corresponding to the regression coefficient is more than 0.05. For this purpose, we build the empirical function:
| (3) |
where
| (4) |
is the probability function and pi is the p-value for the ith variable. The parameters for the probability function (slope 50 and offset −0.1) were chosen so that the same (rewarding) weight of 0 was given to all variables with a p-value less than 0.05, and the same (penalizing) weight of 1 was given to all variables with a p-value above 0.15. Variables with p-values between 0.05 and 0.15 were given a weight that is an increasing function of their p-value, as shown in Fig. 2.
Figure 2.
Second term of the fitness function: empirical function of the p-value for the regression coefficients, rewarding models with statistically significant variables.
The overall fitness function is then given by the sum of the two terms:
| (5) |
where X represents the set of variables in the individual, r is the predictive power criterion (AUC or Spearman correlation coefficient), and ρ is an adjustable coefficient, assigned to the p-value weight function θ. The coefficient allows the user to trade off between the two goals of AUC∕Spearman maximization and statistical relevance, thereby factoring in some degree of overfit prevention. Overfitting results from the selection of too many variables, causing the model to fit the underlying mechanism as well as the noise in the data.
Since the overall fitness function F decreases with increasing model quality, it is best to think of it as a penalty function. The algorithm seeks to minimize that function, in order to extract the model that yields the lowest penalty.
Selection
All models in the population are then ranked according to their penalty, i.e., their ability to predict the outcome. A number of them are selected to become parents for the next generation, which is also required to be of size N. The top two scoring individuals are automatically present in the next generation, unmodified. The N−2 remaining offspring come from either crossover or mutation of selected parents (selected as explained later). Crossover offspring models contain variables from two parents, each variable being randomly inherited from one of the parents. Mutation offspring models are produced from one parent, by giving each variable a chance to be replaced by another randomly chosen variable with a given probability, called the mutation rate. In both operations, the resulting offspring individuals are a set of n unique variables. The ratio xf of crossover versus mutation offsprings is defined through the crossover fraction parameter during the initialization process. Therefore, the number of parents needed to produce N−2 offspring is 2xf(N−2) for the crossover children and (1−xf) (N−2) for the mutation children.
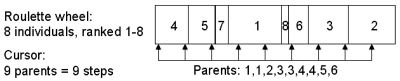
These parents are selected via stochastic uniform sampling. Each parent is first assigned an “expectation,” which is inversely proportional to its ranking in the population according to the fitness score. The probability for a particular individual to be selected as a parent to the next generation is then proportional to that expectation. The selection follows a “roulette wheel” method: each slot of the wheel represents an individual, and the length of the slot is equal to its expectation. A cursor steps through the entire length of the wheel with as many steps as the number of parents needed. The parent is created from each slot in which the cursor lands. Each individual can be selected several times as a parent. The process is illustrated in Fig. 3, with a population of eight individuals with a crossover fraction of 0.5. The required number of parents is then nine. In this example, the two lowest ranking individuals are not selected as parents.
Figure 3.
Selection of parents: stochastic uniform sampling using the roulette wheel method. The example shows a population of eight individuals, ranked 1–8 according to their fitness score. The crossover fraction is 0.5, therefore nine parents must be selected. The cursor selects nine locations in equal steps through the wheel, ensuring the individuals with a higher score have a greater probability of being selected.
Stopping criteria
The process described above of selecting parents, creating offspring, and evaluating the fitness for each of the individuals converges to a population where the “weak” individuals have been eliminated, and the “fittest” ones survive. The process is repeated until the best individual in the population converges to an optimal solution, i.e., until one of these criteria is met:
-
1.
A user-specified maximum number of generations is reached;
-
2.
The lowest penalty has not changed over 50 generations.
Model order ranking
After running for each model order, a leave-one-out cross-validation technique is employed on the best model for that model order. One data point, corresponding to one patient in the database, is left out; the regression correlation coefficients are then calculated on the truncated data set, and the outcome probability corresponding to this model is calculated on the left-out data point. The process is repeated as many times as there are patients in the database, and the probability distribution is compared to the observed outcome distribution using Spearman rank correlation. In the end, the model orders are ranked according to the fitness score described in Eq. 5, where the predicting power criterion is the correlation coefficient calculated in the cross-validation step. The best model for each model order is available in the output of EUCLID.
Patient data
To test the potential of genetic algorithms for the purpose of selecting the variables that are most predictive of a given outcome, we used a data set that investigated the incidence of lung injury in NSCLC patients treated with 3DCRT.18, 19 This IRB-approved prospective study collected data on 200 patients at Duke University Medical Center between 1991 and 1999, 39 of whom developed radiation-induced pneumonitis (RP) of Grade 2 or more. The grades of RP were defined as follows: Grade 0 (no increase in pulmonary symptoms due to RT), Grade 1 (RT-induced pulmonary symptoms not requiring initiation or increase in steroids and∕or oxygen), Grade 2 (RT-induced pulmonary symptoms requiring initiation or increase in steroids), Grade 3 (RT-induced pulmonary symptoms requiring oxygen), and Grade 4 (RT-induced pulmonary symptoms requiring assisted ventilation or causing death). Patients were treated with anterior-posterior beams followed by off-cord oblique parallel opposed boost beams, or multiple noncoplanar, nonaxial beams. Eighty-five percent of patients received a dose above 60 Gy (range 26–86 Gy).
The clinical, biological, and physiological input factors were gender, age, ethnicity (white∕black), performance status, site of disease (central∕peripheral), tobacco use at the time of referral (yes∕no), location of disease inside the lung (lobe), intent (curative∕palliative), surgery (yes∕no), lung volume, forced expiratory volume in 1s (FEV1) prior to RT, prescribed dose, and delivered dose. Additionally, dosimetric variables were extracted from the lung DVH of each patient’s treatment plan: normal tissue complication probability (NTCP), mean lung dose, maximum dose, and V30. V10 to V90 were also considered in increments of 10, but as those quantities were highly correlated, only V30 was included in the multivariate analysis as it showed the highest degree of correlation with RP in univariate analysis. Of the 200 patients included in the study, only 133 had an entry for all 17 variables, 28 of whom developed RP of grade 2 or more. The data were analyzed with the genetic algorithm in EUCLID, for model orders 2 to 12. The modeled outcome was the probability to develop RP of grade 2 or greater. Five different versions of the fitness function were used, with different p-value weight factors ρ=0, 0.25, 0.5, 0.75, and 1. Both fitness criteria (AUC and Spearman correlation coefficient), were compared.
With the 17 variables in this test data set, there are a total of 127 840 combinations that contain 2 to 12 variables. To study the influence of the different GA parameters (population size, crossover fraction and mutation rate), all 127 840 possible combinations of variables were tested with the same penalty function, and the best combination for each model order was used as a baseline for comparison to the GA. Population sizes of 20, 40, 60, 80, and 100 were tested, as well as crossover fractions of 0, 0.25, 0.5, 0.75, and 1. Mutation rates of 0, 0.05, 0.1, and 0.2 were also tested.
The same data were also analyzed using the DREES software,10 which utilizes a sequential forward algorithm for variable selection,12 along with a leave-one-out cross-validation technique. At each model order, models are ranked according to the frequency in which they were selected as the best model in the cross-validation process. Model orders are then ranked based on the Spearman’s correlation coefficient of the best model.
RESULTS
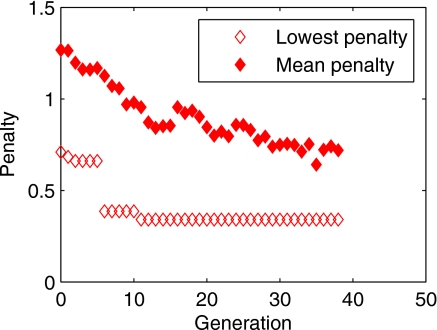
Figure 4 shows the evolution of the population’s mean and lowest penalty as a function of generations, for model order 3. The overall decrease of the mean penalty shows evidence that the GA process eliminates models with low predictive power in favor of models with high predictive power. The automatic selection of the top two individuals to be present unchanged in the next generation ensures that the best individual of each generation is not weaker than the best individual of the previous generation, which is illustrated by the monotonic decrease of the lowest penalty.
Figure 4.
Evolution generation after generation of the population’s lowest and mean penalty, for model order 3. “Survival of the fittest” is evidenced by the overall decrease of the mean penalty (final mean penalty 0.719), and the monotonic decrease of the lowest penalty (final lowest penalty 0.341) illustrates the fact that a generation’s best individual always survives into the next generation.
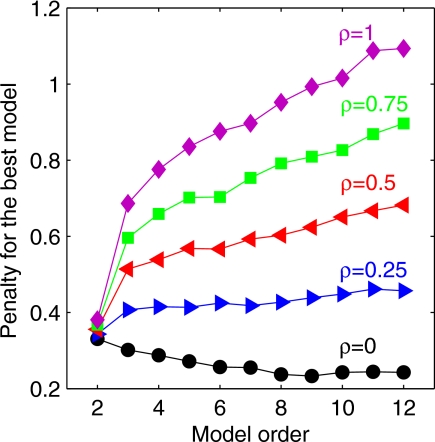
The lowest penalty for each model order with the EUCLID GA is shown in Fig. 5, for model orders 2 to 12, for the five different values of weighting factor ρ. No difference in model order ranking or model selection was observed between the use of the area under the ROC or of the Spearman coefficient as the predicting power criterion. If the statistical significance of the selected variables is not taken into account (ρ=0), the penalty, which depends solely on the predicting power, decreases as model order increases. For ρ=1 (equal importance given to predictive power and statistical significance), the models with more than two variables are penalized by the inclusion of one or several variables with a high p-value.
Figure 5.
Penalty score of the best model as a function of model order, for different weight factors ρ=0, 0.25, 0.5, 0.75, and 1. As the weight of the p-value function increases, higher model orders are penalized more because they involve more nonsignificant variables.
For the size of the tested data set (up to 12 variables to choose among 17 available variables), it was found that a population size of 80 individuals (combinations of variables) can be used to yield results that are identical to the optimal baseline for nearly all model orders. With a population size of 20 or 40, the GA converged to a nonoptimal model, particularly at high model order. Convergence to the best model could not be achieved if the crossover fraction was below 0.5. Likewise, if the crossover fraction was set to 1, or if the mutation rate was set to 0, that is no mutation can occur in either case, the GA did not always extract the best model.
Table 1 shows the list of the variables selected by the algorithms for their best models, at each model order between 1 and 6, for a crossover fraction of 0.8 and a mutation rate of 0.1, with a population size of 80, using the AUC as the predicting power criterion. Ongoing use of tobacco at time of referral and a dosimetric variable, most often V30, are present in every model, with a p-value of 0.07 or less in every case (lower doses lead to less injury, as well as the use of tobacco, as was reported for rats21 and humans18, 22, 23). All additional variables in higher model orders systematically have a p-value greater than 0.1, showing that no statistically significant correlation can be derived between these variables and the occurrence of RP. As illustrated by the baseline computation, where all possible combinations of variables are tested, the actual best model was selected by the GA for models with up to five variables. It should be noted that because the baseline uses the same penalty function as the GA, the best model as determined by the baseline may have a predictive power that is lower than that of the GA, due to the presence of more statistically significant variables. For example, in Table 1, the model with order 6 selected by the baseline method has an AUC of 0.71, which is lower than that of the GA (0.73). However, the baseline includes only two variables with a p-value higher than 0.15 (maximum dose and gender), while the GA best model includes three (pre-RT FEV1, surgery, and prescribed dose). Included also in Table 1 are the results of the analysis of the same data using the sequential algorithm of DREES.
Table 1.
Variables selected by the GA, the baseline, and DREES for the best model at each model order, with the variables’ respective p-value, and the model’s AUC, Spearman rank correlation coefficient, and fitness score (using AUC as predicting power and assuming ρ=1).
| N | GA (EUCLID) | Baseline | Sequential (DREES) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Variables | p | AUC | Rs | F | Variables | p | AUC | Rs | F | Variables | p | AUC | Rs | Fa | |
| 2 | V30 | 0.048 | 0.670 | 0.231 | 0.381 | V30 | 0.048 | 0.670 | 0.231 | 0.381 | V30 | 0.048 | 0.670 | 0.231 | 0.381 |
| Tobacco use | 0.074 | Tobacco use | 0.074 | Tobacco use | 0.074 | ||||||||||
| 3 | V30 | 0.049 | 0.657 | 0.267 | 0.687 | V30 | 0.049 | 0.657 | 0.267 | 0.687 | V30 | 0.063 | 0.644 | 0.227 | 0.817 |
| Tobacco use | 0.066 | Tobacco use | 0.066 | Tobacco use | 0.092 | ||||||||||
| Ethnicity | 0.143 | Ethnicity | 0.143 | Goal | 0.200 | ||||||||||
| 4 | V30 | 0.015 | 0.693 | 0.285 | 0.776 | V30 | 0.015 | 0.693 | 0.285 | 0.776 | V30 | 0.015 | 0.693 | 0.285 | 0.776 |
| Tobacco use | 0.077 | Tobacco use | 0.077 | Tobacco use | 0.077 | ||||||||||
| Ethnicity | 0.114 | Ethnicity | 0.114 | Ethnicity | 0.114 | ||||||||||
| Pre-RT FEV1 | 0.183 | Pre-RT FEV1 | 0.183 | Pre-RT FEV1 | 0.183 | ||||||||||
| 5 | V30 | 0.019 | 0.699 | 0.310 | 0.835 | V30 | 0.019 | 0.699 | 0.310 | 0.835 | V30 | 0.019 | 0.699 | 0.310 | 0.835 |
| Tobacco use | 0.075 | Tobacco use | 0.075 | Tobacco use | 0.075 | ||||||||||
| Ethnicity | 0.104 | Ethnicity | 0.104 | Ethnicity | 0.104 | ||||||||||
| Pre-RT FEV1 | 0.210 | Pre-RT FEV1 | 0.210 | Pre-RT FEV1 | 0.210 | ||||||||||
| Surgery | 0.500 | Surgery | 0.500 | Surgery | 0.500 | ||||||||||
| 6 | NTCP | 0.032 | 0.725 | 0.306 | 0.876 | V30 | 0.022 | 0.707 | 0.254 | 0.840 | V30 | 0.051 | 0.695 | 0.280 | 0.997 |
| Tobacco use | 0.006 | Pre-RT FEV1 | 0.085 | Tobacco use | 0.080 | ||||||||||
| Ethnicity | 0.104 | Ethnicity | 0.140 | Ethnicity | 0.116 | ||||||||||
| Pre-RT FEV1 | 0.380 | MLD | 0.088 | Surgery | 0.490 | ||||||||||
| Surgery | 0.367 | Max dose | 0.250 | Goal | 0.310 | ||||||||||
| Prescribed dose | 0.179 | Gender | 0.614 | Site | 0.550 | ||||||||||
Note: N=model order; Rs=Spearman rank correlation coefficient; F=fitness score; MLD=mean lung dose.
In DREES, the selection criteria for model order selection is the Spearman rank correlation coefficient. Therefore, the fitness score in the DREES column is not actually used in model evaluation, but it is given here for completeness.
Table 2 presents a univariate analysis of those two variables that were singled out by the GA: it shows the percentage of patients developing RP of grade ⩾2, for those who have a V30 greater than 30% as opposed to those who have a V30 less than 30%, and for those who used tobacco at time of referral as opposed to those who did not.
Table 2.
Univariate analysis of the V30 and the use of tobacco at time of referral: percentage of patients developing RP of grade ⩾2 for each category listed in the first column.
| RP grade ⩾2 (%) | p-value | |
|---|---|---|
| V30>30% | 30 | 0.004 |
| V30⩽30% | 12 | |
| Tobacco use | 9 | 0.09 |
| No tobacco use | 21 |
DISCUSSION
The two pitfalls of variable selection are underfitting (too few variables), which can underestimate the predicting power of the model, and overfitting (too many variables), which tends to fit fluctuations unrelated to the biological effect. This is illustrated in Fig. 5, when comparing the ρ=0 and ρ=1 curves. When the statistical significance of the variables is not taken into account, the model quality seemingly increases with model order. Thus, it appears that the more variables the better. However a closer look at the quality of the added variables shows that since the statistical significance of their correlation with the outcome is poor (p>0.1), these variables are not truly related to the biological effect under consideration, therefore, actually undermining the quality of the model while increasing its complexity. In our view, the ranking provided by the penalty function that includes the p-value weight (ρ=1) is better suited for the purpose of radiobiological modeling, as it implicitly restricts overfitting. In that respect, the penalty function used in EUCLID is better than the one use by Vinterbo and Ohno-Machado,16 because it eliminates variables with high p-values, while their implementation penalizes models with a high number of variables, regardless of their statistical significance. For comparison, the sequential algorithm in DREES, with the leave-one-out cross-validation, selected the same models as the GA for each model order, or models that differed only by a nonsignificant variable, but ranked the model with five variables the highest, despite the fact that it included three variables with high p-value.
The results of Table 1 show the stability of the variables that are actually related to the outcome (in our example case, a dosimetric variable and tobacco use), in that they are present with a low p-value at all model orders. A previous analysis of the same data18 reached the same conclusion, using a different approach. Analyzing 11 variables, they established the univariate correlation between each variable and the occurrence of RP. They then included in the logistic regression fit only those variables whose correlation with RP was statistically significant, to verify that the correlation held in the multivariate approach. Furthermore, the data were analyzed using DREES, which also singled out the importance of dosimetric variables and tobacco use, while using a different variable selection approach. However, in the typical use of DREES, the optimal model order is calculated before the best model is extracted for that model order; therefore, no comparison is possible between model orders. The output format of the EUCLID GA, where the best model for every model order is given, presents the advantage that the physician or physicist can use their judgment over the results when deciding what model to apply ultimately, and what variables to use.
It is important to note that the GA is not a tool designed to measure the predicting power of a model. The estimation of that predicting power can only be as good as the fit function used, in our case a logistic regression. In the example described above, it was not the GA that established that ongoing tobacco use at time of referral was correlated with the occurrence of RP: it was the logistic regression fit, which derived a regression coefficient and an associated p-value, establishing statistical significance. However, for any given fit function, the GA attempts to find which parameters of that function will lead to the highest correlation. Therefore, in our example, the role of the GA was to prove that models that included tobacco use as a parameter were more predicting than models that did not include it. While increasing the number of variables in a logistic regression model may artificially increase the predicting power of that model by including more variables that may not have a statistically significant correlation with the outcome (overfitting), providing a large number of variables as input to the GA allows the algorithm to actually test more variables. The implicit safeguard against overfitting provided by the second term of the penalty function ensures that out of that large number of variables, only a few statistically significant variables will stand out in a low model order regression fit.
The limitations of genetic algorithms have been discussed in the literature.14, 24 The effectiveness of the GA in finding a solution to a given problem is highly dependent upon the choice of the fitness function and the algorithm parameters. While a powerful aspect of genetic algorithms is that they explore several areas of the search space towards the optimal solution at the same time, there still exists a risk that a locally optimal solution emerges and reproduces at such a rapid rate, that convergence will be attained too early. It is the role of the mutation operation to open new search areas, to ensure that all good solutions are analyzed.
For a data set containing 30 variables, there are above 50 million different combinations containing 1 to 10 variables. Given then a reasonably fast computer (3.8 GHz) takes about 0.01 s to perform one fit, it would take almost 6 days to apply the “brute force” method. It can be pointed out that in outcome analysis, computing time is not an issue; therefore, the “brute force” method used here as the baseline can always be applied, given enough time and∕or computing power. During execution of the GA, with an initial population of 80, if 100 generations are needed to achieve convergence at each model order, only 80 000 combinations are calculated, which reduces the time to approximately 15 min. Therefore, the GA offers a time-competitive solution for a preliminary analysis, which may guide the user to concentrate on the right set of variables in a relatively short time.
It should be emphasized that as in biological evolution, genetic algorithms are not necessarily designed to extract the best solution, but to find a “close to best” solution. When comparing the results of the GA with the search of all possible combinations, it was found that at low model order, the actual best solution was always found by the GA, but at higher model order that included variables with high p-values, only a model close to the best model was extracted, with one variable substituted for another. This is an intrinsic property of the penalty function we chose: a statistically significant variable, such as tobacco use, increases the value of the predicting power as measured by the area under the ROC, while its low p-value does not add anything to the penalty. Therefore, the GA is very likely to identify it as part of the optimal solution. On the other end, a nonsignificant variable, such as gender, adds little to the predicting power, and the function used in Eq. 3 gives equal weight to all high p-value variables. Thus, the overall penalty will not change greatly if another variable, for example, age, is substituted, and the GA will satisfy itself with this “close to best” solution. Ultimately the important criteria in radiobiological modeling is the statistical significance; therefore, the GA is well suited to extract the optimal model.
CONCLUSIONS
We developed a genetic algorithm as an automated process of variable selection for logistic regression analysis in EUCLID. We tested the algorithm on a study of radiation-induced pneumonitis in lung cancer patients, and compared it with all possible combinations of variables. We found that the GA successfully identified as the best model the combination with only low p-values that yielded the highest predicting power. The second term in the penalty function of the genetic algorithm, which accounts for the statistical significance of the variables selected, appears to implicitly restrict overfitting. Our results show that the use of a genetic algorithm provides a robust and efficient approach to multivariate analysis and prediction of radiotherapy treatment outcome.
ACKNOWLEDGMENTS
The authors would like to thank Dr. J. O. Deasy and Dr. I. El Naqa from Washington University School of Medicine, for sharing their own software, DREES, on which EUCLID was developed. The authors SKD, SZ, and LBM were partially supported by NIH Grant Nos. R01 CA 115748 and R01 CA69579.
References
- Webb S. and Nahum A. E., “A model calculating tumor control probability in radiotherapy including the effects of inhomogeneous distributions of dose and clonogenic cell density,” Phys. Med. Biol. 10.1088/0031-9155/38/6/001 38, 653–666 (1993). [DOI] [PubMed] [Google Scholar]
- Burman B. C., Kutcher G. J., Emami B., and Goitein M., “Fitting of normal tissue tolerance data to an analytic function,” Int. J. Radiat. Oncol., Biol., Phys. 21, 123–135 (1991). [DOI] [PubMed] [Google Scholar]
- Lyman J. T., “Complication probability as assessed from dose-volume histograms,” Radiat. Res. 10.2307/3576626 104, S13–S19 (1985). [DOI] [PubMed] [Google Scholar]
- Sanchez-Nieto B. and Nahum A. E., “BIOPLAN: Software for the biological evaluation of radiotherapy treatment plans,” Med. Dosim. 25, 71–76 (2000). [DOI] [PubMed] [Google Scholar]
- Warkentin B., Stavrev P., Stavreva N., Field C., and Fallone B. G., “A TCP-NTCP estimation module using DVHs and known radiobiological models and parameter sets,” Cryst. Prop. Prep. 5, 50–63 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S., Zhou S., Yin F.-F., Marks L. B., and Das S. K., “Using patient data similarities to predict radiation pneumonitis via a self-organizing map,” Phys. Med. Biol. 10.1088/0031-9155/53/1/014 53, 203–216 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S., Zhou S., Yin F.-F., Marks L. B., and Das S. K., “Investigation of the support vector machine algorithm to predict lung radiation-induced pneumonitis,” Med. Phys. 10.1118/1.2776669 34, 3808–3814 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S., Zhou S., Zhang J., Yin F.-F., Marks L. B., and Das S. K., “A neural network model to predict lung radiation-induced pneumonitis,” Med. Phys. 10.1118/1.2759601 34, 3420–3427 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das S. K. et al. “Predicting lung radiotherapy-induced pneumonitis using a model combining parametric lyman probit with nonparametric decision trees,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/j.ijrobp.2007.03.064 68, 1212–1221 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- El Naqa I., Suneja G., Lindsay P. E., Hope A. G., Alaly J. R., Vicic M., Bradley J. D., Apte A., and Deasy J. O., “Dose response explorer: An integrated open-source tool for exploring and modeling radiotherapy dose-volume outcome relationships,” Phys. Med. Biol. 10.1088/0031-9155/51/22/001 51, 5719–5735 (2006). [DOI] [PubMed] [Google Scholar]
- Gayou O., Parda D. S., and Miften M., “EUCLID: An outcome analysis tool for high-dimensional clinical studies,” Phys. Med. Biol. 10.1088/0031-9155/52/6/011 52, 1705–1719 (2007). [DOI] [PubMed] [Google Scholar]
- El Naqa I., Bradley J., Bianco A. I., Lindsay P. E., Vicic M., Hope A., and Deasy J. O., “Multivariate modeling of radiotherapy outcomes, including dose-volume and clinical factors,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/j.ijrobp.2005.11.022 64, 1275–1286 (2006). [DOI] [PubMed] [Google Scholar]
- Michalewicz Z., Genetic Algorithms + Data Structures = Evolution Programs (Springer, New York, 1992). [Google Scholar]
- Mitchell M., An Introduction to Genetic Algorithms (MIT Press, Cambridge, MA, 1996). [Google Scholar]
- Coley D. A., An Introduction to Genetic Algorithms for Scientists and Engineers (World Scientific, London, 1999). [Google Scholar]
- Vinterbo S. and Ohno-Machado L., “A genetic algorithm to select variables in logistic regression: Example in the domain of myocardial infarction,” Proceedings of the 1999 AMIA Annual Symposium, pp. 984–988. [PMC free article] [PubMed]
- Hanley J. A. and McNeil B. J., “A method of comparing the areas under receiver-operating characteristic curves derived from the same cases,” Radiology 148, 839–843 (1983). [DOI] [PubMed] [Google Scholar]
- Hernando M. L., Marks L. B., Bentel G. C., Zhou S.-M., Hollis D., Das S. K., Fan M., Munley M. T., Shafman T. D., Anscher M. S., and Lind P. A., “Radiation-induced pulmonary toxicity: A dose-volume histogram analysis in 201 patients with lung cancer,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/S0360-3016(01)01685-6 51, 650–659 (2001). [DOI] [PubMed] [Google Scholar]
- Etiz D., Marks L. B., Zhou S.-M., Bentel G. C., Clough R., Hernando M. L., and Lind P. A., “Influence of tumor volume on survival in patients irradiated for non-small-cell lung cancer,” Int. J. Radiat. Oncol., Biol., Phys. 53, 835–846 (2002). [DOI] [PubMed] [Google Scholar]
- Matthews D. E. and Farewell V. T., Using and Understanding Medical Statistics, 3rd ed. (Karger, Basel, Switzerland, 1996). [Google Scholar]
- Nilsson K., Henriksson R., Cai Y. Q., Hellström S., Hörnqvist Bylunds S., and Bjermer L., “Effects of tobacco-smoke on radiation-induced pneumonitis in rats,” Int. J. Radiat. Biol. 62, 719–727 (1992). [DOI] [PubMed] [Google Scholar]
- Johansson S., Bjermer L., Franzen L., and Henriksson R., “Effects of ongoing smoking on the development of radiation-induced pneumonitis in breast cancer and oesophagus cancer patients,” Radiother. Oncol. 49, 41–47 (1998). [DOI] [PubMed] [Google Scholar]
- Bejmer L., Hallgren R., Nilsson K., Franzen L., Sandström T., Särnstrand B., and Henriksson R., “Radiation-induced increase in hyaluronan and fibronectin in bronchoalveolar lavage fluid from breast cancer is suppressed by smoking,” Eur. Respir. J. 5, 785–790 (1992). [PubMed] [Google Scholar]
- Forrest S., “Genetic algorithms: Principles of natural selection applied to computation,” Science 10.1126/science.8346439 261, 872–878 (1993). [DOI] [PubMed] [Google Scholar]