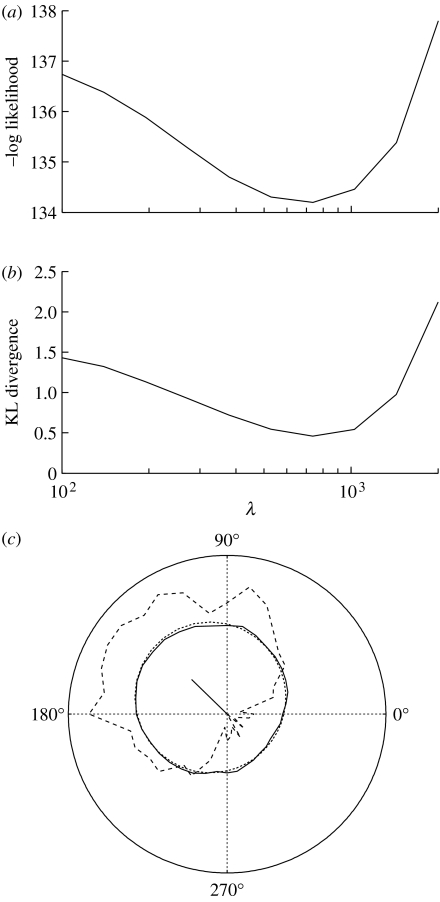
Figure 2.

Evaluating cross-validation method for estimating the value of the smoothing parameter λ. Results for the simulated observer's data shown in (c) for σ=1. See appendix B. (a) At each sampled value of λ, three quarters of the data were used to estimate the prior. Using this prior, the likelihood of the remaining quarter was evaluated using equation (2.23), where σ=1. This was repeated once for each of four disjoint quarters, and the mean of the four resultant likelihood functions is plotted here. The minimum with respect to the negative log likelihood corresponds to λ≈700. (b) To evaluate the success of cross-validation for each sampled value λ_j of λ, the Kullback–Leibler (KL) divergence between the known prior $p_{\theta }^{*}(\theta )$ of this simulated observer and the prior ${\hat{p}}_{\theta }(\theta )$ obtained with λ_j was calculated as $E_{\text{KL}}=1000\times \mathrm{\Delta }\theta \sum {\hat{p}}_{\mathrm{\theta }}({\theta }_i)\text{log}{\hat{p}}_{\mathrm{\theta }}({\theta }_i)/p_{\theta }^{*}({\theta }_i),$ where i=(0, 10, …, 350), θ_i=10×i and Δθ=10°. The minimum with respect to the KL distance also corresponds to λ≈700, confirming that cross-validation chooses a value of λ, which provides a good estimate of the true prior. (c) Estimating the light-from-above prior p_θ(θ) for a simulated observer. The lighting direction varies around the circle, and the probability that the stimulus was judged to be convex varies with distance from the origin. The graph shows (i) a sample from the posterior p(c₀|x) as the proportion of convex responses (dashed), (ii) the known prior (dotted), (iii) the estimated prior (solid), based on the proportion of convex responses, as it would be for a human observer, and (iv) the mean vector (solid line), which is the mean of the prior (see appendix C). The direction of this vector indicates the bias in the prior, and its length shows the amount of bias (see appendix A). The simulated observer was exposed to the same 36 lighting directions and the same number of trials per lighting direction (32) as the human observers used in the experiment described in the text, a discrimination parameter that was set at σ^*=1 dB and a concavity preference set at p(c₁)=0.5. The value of the smoothing parameter estimated from cross-validation is λ=700 (see (a) and (b)). Using λ=700 and σ=1, the concavity preference was estimated as $\hat{p}(c_1)=0.507$.