A serial founder effect model for human settlement out of Africa

Abstract

The increasing abundance of human genetic data has shown that the geographical patterns of worldwide genetic diversity are best explained by human expansion out of Africa. This expansion is modelled well by prolonged migration from a single origin in Africa with multiple subsequent serial founding events. We discuss a new simulation model for the serial founder effect out of Africa and compare it with results from previous studies. Unlike previous models, we distinguish colonization events from the continued exchange of people between occupied territories as a result of mating. We conduct a search through parameter space to estimate the range of parameter values that best explain key statistics from published data on worldwide variation in microsatellites. The range of parameters we use is chosen to be compatible with an out-of-Africa migration at 50–60 Kyr ago and archaeo–ethno–demographic information. In addition to a colonization rate of 0.09–0.18, for an acceptable fit to the published microsatellite data, incorporation into existing models of exchange between neighbouring populations is essential, but at a very low rate. A linear decay of genetic diversity with geographical distance from the origin of expansion could apply to any species, especially if it moved recently into new geographical niches.

1. Introduction

Geographical expansion by a population may be due to a fitness advantage in its rate of survival and/or a higher reproduction rate that results in successful invasion of neighbouring regions. Expansion to previously uninhabited or sparsely inhabited areas will not create competition with resident populations. Homo sapiens is an especially successful species that is both invasive and cosmopolitan. Human evolution and expansion can be studied using information from archaeology, linguistics and genetics. The increasing wealth of human genetic data, in particular, may shed light on the process of human expansion.

One such set of data included 1048 individuals from the HGDP–CEPH Human Genome Diversity Cell Line Panel (Cann et al. 2002), each of whom was genotyped for 783 autosomal microsatellite loci (Ramachandran et al. 2005), which included the 377 loci from Marshfield screening set no. 10 previously studied by Rosenberg et al. (2002). The average heterozygosity at these microsatellite loci decreases linearly with geographical distance from East Africa (Prugnolle et al. 2005; Ramachandran et al. 2005). This pattern is not seen so strongly for any initial site outside of East Africa, much less so for any non-African site chosen as the origin. Such a pattern is best explained as being due to a ‘serial founder effect’, because simulations of the spread of genotypes along a linear path have produced heterozygosity patterns and values similar to those observed in the dataset (Ramachandran et al. 2005; Liu et al. 2006). For some phenotypes, a parallel decline with that of genetic variability is also seen (Manica et al. 2007). The worldwide expansion of humans out of Africa probably happened in many small steps—each step involving a small sample of founders from the population at the front of expansion. This series of founder effects would have led to a stepwise increase in genetic drift and a corresponding decrease in genetic diversity.

In this paper, we discuss a new simulation model for the serial founder effect out of Africa and compare it with results from previous studies. We discuss how our simulation model improves upon some aspects of the previous models. In addition to a colonization rate of 0.09–0.18 for an acceptable fit to the published microsatellite data, exchange between neighbouring populations is essential, but at a very low rate. We also compare results already available from the microsatellite data with new ones derived from tests with a large number of single nucleotide polymorphisms (SNPs).

2. Features of the simulation model

The expansion of a population can be described by two models, neither of which is perfect, but which give similar results. The continuous model, also called the ‘wave of advance’ model (Ammerman & Cavalli-Sforza 1984), was first suggested by Fisher (1937) for the geographical spread of advantageous genes. It was later extended to population expansions (Skellam 1951), with population growth and local migratory activity represented as a diffusion process that takes the form of a population wave expanding outwards at a steady radial rate. The model, which also entails that the velocity of the spread is proportional to the square root of the product of the rate of population growth and the rate of migration, makes two main assumptions. First, growth occurs in a logistic manner—initially, the growth of a population takes place at an exponential rate, but gradually slows over time as the population approaches a saturation level. Second, migration takes place at a constant rate in time and according to a random walk process. Although this model is interesting and also produces a linear expansion of populations in space and time, it deals with migration of individuals and does not give due importance to the social reality of human migration, which, especially in the occupation of empty territory, would involve groups of varying size. In our first paper on the serial founder effect (Ramachandran et al. 2005) we therefore focused on a second idealization of the process of migration and expansion of a population: the discrete model, also called the ‘stepping stone’ model, the linear version of which considers an approximately one-dimensional distribution of populations (along a coastline, in a narrow mountain valley, along a river, etc.). The world is clearly not one-dimensional, but if several relatively independent migration waves occurred, and especially if they all started from a single origin, as is widely agreed upon, then their aggregate can be approximately represented by a one-dimensional expansion.

In this paper, we model a population as a set of diploid individuals. Each individual has two copies of 783 microsatellite genes (Ramachandran et al. 2005). A microsatellite is represented by the number of repeats of the basic motif of DNA letters, and mutation increases or decreases the number of repeats by 1 with equal probability. This is the symmetric stepwise mutation model. However, the different alleles of a microsatellite, which correspond to the different possible numbers of repeats, have a finite range of variation—up to a maximum of 36 repeats in our simulation. The effective mutation rate is 0.0007567 per site per individual per generation (Zhivotovsky et al. 2003; Ramachandran et al. 2005).

Each simulated population is called a deme, and its growth follows a logistic dynamic with a value of 1.8 for the initial growth rate, until it reaches its carrying capacity, which is the maximum size of the population that the environment of the deme can sustain. This growth rate assumes a pre-reproductive mortality of approximately 40–50% for hunter–gatherers in stationary hunter–gatherer populations, based on observations in African pygmies (Cavalli-Sforza 1986). We varied the carrying capacity along with other parameters to see what ranges provide a close fit to the HGDP–CEPH microsatellite data.

The population size in generation (t+1) is given by

$$N_{t+1}=N_t\times f(N_t),$$ (2.1)

where N_t is the population size in generation t and f(N_t) is the instantaneous growth rate for that generation t, which we assume is given by

$$f(N_t)=1.8(1-N_t/K)+N_t/K,$$ (2.2)

where K is the carrying capacity of the deme. The maximum value of f(N_t) is 1.8 when N_t∼0, i.e. the deme is almost empty. The minimum value of f(N_t) is 1 when the deme is saturated, i.e. N_t=K.

Once the population size of the next generation is determined, reproduction is carried out according to Mendelian laws of inheritance. A child is created by choosing two individuals at random from the population to be its parents. Each microsatellite locus exists in two copies: one copy is inherited from the individual's mother and the other copy from the father. A child is equally likely to inherit its maternal copy from its mother's father as from its mother's mother. It is equally likely to inherit its paternal copy from its father's father as from its father's mother. The inheritance of each microsatellite is independent of all others.

We model the world as a one-dimensional array of such populations, each with the same carrying capacity. Since the origin of human expansion was probably at some place in East Africa (Ramachandran et al. 2005), there was room for expansion from there to outside of Africa as well as to other places within Africa such as sub-Saharan Africa. We therefore place the origin of expansion not at the left edge of the array of demes but towards the interior. We have a total of 251 demes (0, 1, 2, …, 250) with deme 50 designated as the origin of expansion, from which the population can expand up to 50 demes to the left (corresponding to other places within Africa) and 200 demes to the right (corresponding to the paths out of Africa).

We assume that the population at the origin of expansion is at its carrying capacity and is initialized according to the distribution of alleles in the aggregate of all the African populations taken from the HGDP–CEPH dataset. From this initial population, a group of 50 people move into the neighbouring demes on the left and right where they increase according to equations (2.1) and (2.2) to the carrying capacities. At this point, there is a ‘left wavefront’ for the population and a ‘right wavefront’. In each direction, a serial founder effect now starts.

A colonization event happens when a group of founders moves out of a deme that is at carrying capacity into the neighbouring deme, which is uninhabited so far. The rate of colonization is defined to be the number of founders divided by the carrying capacity, and is the fraction of people in the population at the frontier that moves into the empty neighbouring deme whenever colonization takes place. Besides colonization, we allow another form of migration, namely the movement of people from one occupied territory into the neighbouring occupied territory. This occurs primarily as a result of individuals moving into neighbouring tribes and mating. We shall call this an ‘exchange’ event. The rate of exchange between demes i and (i+1) is defined to be the fraction of the population that migrates into the neighbouring deme every generation. If both the populations are at carrying capacity, and if the rate of exchange is m (0≤m≤1), then Km people migrate from deme i to deme (i+1) and Km people move from deme (i+1) into deme i in that generation. In our simulations, the rate of colonization, the logistic growth rate and the carrying capacities of the populations completely determine the velocity of the wavefront, which in turn determines the number of generations it will take for the wavefront to reach the boundary of the array of demes. It would be unrealistic for the rate of exchange of people between two neighbouring demes to influence the velocity of the wavefront. To ensure that such a thing does not happen, we add the constraint that there is gene flow between neighbouring populations only when both the populations are at carrying capacity. This means that until the deme at the wavefront achieves its carrying capacity, we do not allow that deme to exchange people with another deme. In this way, we cleanly separate the effects of the colonization rate from the effects of exchange rate. The colonization rate influences the velocity of the wavefront and the magnitude of drift at the wavefront. The exchange rate determines the level of admixture between the populations due to mating and has nothing to do with colonization.

After the entire array of demes has been colonized, we allow the simulations to continue for 400 more generations. This is to account for the last 10–12 Kyr of human history subsequent to the initiation of agriculture and human settlements (and approximately the time since humans reached the southern tip of South America, which corresponds to deme 250).

In our simulations, we varied the values of the carrying capacity, the colonization rate and the exchange rate in order to compare the results with the observed data (Ramachandran et al. 2005). The number of generations from the out-of-Africa event until the end also varied across our simulation trials, but is not an independent parameter. The number of generations during the colonization phase is determined by the velocity of the wavefront of the population, and the number of demes in the linear array between the origin of expansion and the farthest deme from the origin.

The equation for the regression line of the variation of heterozygosity with geographical distance from a possible origin in East Africa obtained by Ramachandran et al. (2005) from the HGDP–CEPH microsatellite dataset is

$$\text{heterozygosity}=0.7682-(6.52\times {10}^{-6})\times (\text{distance}\text{from}\text{Addis}\text{Ababa}\text{in}\text{km}).$$ (2.3)

We attempted to determine what range of parameter values would produce results from our simulations similar to these observed values for the slope and intercept of the regression line given by equation (2.3). A distance of 200 demes corresponds to the distance from the origin of expansion to the southernmost population of South America (approx. 25 000 km), which means that each deme corresponds to an approximate area of 125×125 km. The maximum distance of Addis Ababa from other places in Africa is a little more than 6000 km, which corresponds to a length of approximately 50 demes. Thus, the left boundary in our array of demes is 50 demes to the left of the origin of expansion, and the right boundary is 200 demes to the right of the origin of expansion. Instead of converting from a distance measured in terms of the number of demes (from the simulation) to a distance measured in km (from the data), it is easier to compare directly the total fall in the heterozygosity from the origin to the end of human expansion from the simulation with that from the data.

For the regression line from the data (Ramachandran et al. 2005), the total observed fall in the heterozygosity from the origin to the southernmost population of South America is (6.52×10⁻⁶)×(distance to the southernmost population of South America from the origin of expansion in East Africa, incorporating waypoints)

$$\begin{array}{l}=(6.52\times {10}^{-6}{\text{km}}^{-1})\times (\sim \mathrm{25\; 000}\text{km})\\ =\mathrm{0.163.}\end{array}$$

The incorporation of waypoints (Ramachandran et al. 2005) forces the measurement of distances between any two points to be along a continuous land route that humans might have used as opposed to traversing bodies of water. For example, the distance between Ethiopia and Brazil should be measured along a path through Asia that travels through the Bering Strait from Siberia into Alaska and then down from there to South America, rather than the great circle distance between Ethiopia and Brazil which cuts across the Atlantic Ocean. The southern tip of South America is a further 3000 km down from the southernmost population in the dataset. This would make the estimate of total distance from Ethiopia to the southern tip of South America approximately 28 000 km, which corresponds to a total fall of 0.183 in the heterozygosity from the origin to the southern tip of South America.

Since we need to allow for uncertainties in our knowledge of the exact location of the origin of modern humans and of the exact distances along the migration paths from the origin to any other location, we aim for a slope of the regression line between 0.76 and 0.78, instead of an exact value of 0.7682, and a fall in heterozygosity between 0.16 and 0.19 in magnitude, instead of an exact value of 0.163 or 0.183.

3. Comparison of the general features of different simulation models

The first attempt at a model incorporating the serial founder effect to explain the observed patterns of variation of heterozygosity over geographical distance was made by Ramachandran et al. (2005). Their simulation results showed that heterozygosity decays linearly with geographical distance from the origin. The differences between that model and our present model are explained in table 1. Liu et al. (2006) estimated various parameters of human expansion based on a simulation model that differs from both Ramachandran et al. (2005) and our present model. The main differences between Liu et al. (2006) and our present model are explained in table 2.

Table 1.

A comparison of the simulation models of Ramachandran et al. (2005) and our present model. (Only major differences are mentioned.)

	Ramachandran et al. (2005)	our present model
number of demes in total	100	251
population growth	exponential growth rate of 1.8 with excess above carrying capacity culled randomly	logistic growth with an initial growth rate of 1.8 that caps at carrying capacity
genome	haploid (Y-chromosome)	diploid
reproduction	genome of child identical to genome of father	genome of child created from genome of parents by Mendelian segregation
colonization rate	one colonization event every 20 generations	variable parameter
number of founders	250	variable parameter; determined by the carrying capacity and the colonization rate
exchange rate	no exchange between neighbouring populations	variable parameter
carrying capacity	above 5000	below 5000; variable parameter
origin of expansion	at the left edge of the deme array	in the interior of the deme array, with 50 demes on the left and 200 on the right

Table 2.

A comparison of the simulation models of Liu et al. (2006) and our present model. (Only major differences are mentioned.)

	Liu et al. (2006)	our present model
number of demes in total	300	251
population growth	logistic growth; initial growth rate variable, and finally estimated to be 1.86	logistic growth with a growth rate fixed at 1.8
carrying capacity	variable parameter; carrying capacity of Africa estimated at 1064; all other demes at 750	variable parameter; all demes have the same carrying capacity
colonization and exchange rate	aggregated under a single value for migration rate, which is variable, and estimated to be 0.115 in each of the two directions	separate; both vary independently
origin of expansion	at the left edge of the array of demes	in the interior of the deme array, with 50 demes on the left and 200 on the right
predicted pattern of variation of heterozygosity with geographical distance from the origin of expansion	nonlinear decay	linear decay with a boundary effect for the populations at the edges of the grid

4. Results and analysis

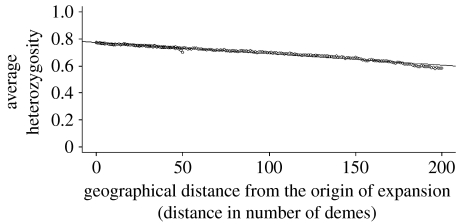
Tables 3–5 show the results from our simulation model for colonization rates of 0.09, 0.13 and 0.18, respectively. In each table, the carrying capacity varies from 400 to 1500 and the exchange rate from 0 to 0.09 (except for three instances with an exchange rate of 0.18). Figure 1 shows the decline in heterozygosity with distance for one of the cases in table 4. The results follow the general patterns explained below.

Table 3.

Results for a colonization rate of 0.09. (The columns contain, respectively, the carrying capacities of all demes, exchange rate, slope measured with respect to the total number of demes and its standard error, intercept and its standard error, total fall in heterozygosity from the origin to the deme farthest from the origin, correlation coefficient between average heterozygosity and geographical distance and the total number of generations up to the end of the simulation.)

carrying capacity	exchange rate	slope	s.e.	intercept	s.e.	fall in heterozygosity	correlation coefficient	total generation
400	0	−2.20×10−4	2.22×10−5	0.4647	2.31×10−3	−0.044	−0.53	2200
400	0.003	−1.08×10−3	1.44×10−5	0.7128	1.49×10−3	−0.215	−0.98	2200
400	0.005	−1.14×10−3	1.25×10−5	0.7390	1.31×10−3	−0.227	−0.99	2200
400	0.01	−1.22×10−3	1.42×10−5	0.7653	1.47×10−3	−0.243	−0.98	2200
400	0.03	−1.31×10−3	1.26×10−5	0.7995	1.32×10−3	−0.262	−0.99	2200
400	0.05	−1.30×10−3	1.12×10−5	0.8091	1.16×10−3	−0.261	−0.99	2200
400	0.07	−1.31×10−3	1.07×10−5	0.8181	1.12×10−3	−0.262	−0.99	2200
400	0.09	−1.31×10−3	1.14×10−5	0.8203	1.18×10−3	−0.262	−0.99	2200
750	0	−3.86×10−4	1.53×10−5	0.5850	1.59×10−3	−0.077	−0.85	2400
750	0.002	−9.82×10−4	1.16×10−5	0.7568	1.21×10−3	−0.197	−0.98	2400
750	0.003	−1.05×10−3	1.15×10−5	0.7794	1.20×10−3	−0.211	−0.99	2400
750	0.005	−1.04×10−3	1.11×10−5	0.7869	1.16×10−3	−0.208	−0.99	2400
750	0.01	−1.12×10−3	1.12×10−5	0.8089	1.17×10−3	−0.224	−0.99	2400
750	0.03	−1.14×10−3	9.68×10−6	0.8301	1.01×10−3	−0.228	−0.99	2400
750	0.05	−1.17×10−3	1.04×10−5	0.8398	1.08×10−3	−0.235	−0.99	2400
750	0.07	−1.18×10−3	1.20×10−5	0.8463	1.25×10−3	−0.237	−0.99	2400
750	0.09	−1.16×10−3	9.67×10−6	0.8459	1.01×10−3	−0.232	−0.99	2400
1000	0.001	−9.37×10−4	9.40×10−6	0.7733	9.78×10−4	−0.187	−0.98	2400
1000	0.002	−9.60×10−4	9.84×10−6	0.7901	1.03×10−3	−0.192	−0.99	2400
1000	0.003	−9.87×10−4	1.00×10−5	0.7999	1.05×10−3	−0.197	−0.99	2400
1000	0.004	−1.01×10−3	9.62×10−6	0.8072	1.00×10−3	−0.203	−0.99	2400
1200	0	−4.28×10−4	1.07×10−5	0.6618	1.11×10−3	−0.086	−0.93	2400
1200	0.001	−8.64×10−4	8.10×10−6	0.7824	8.43×10−4	−0.173	−0.99	2400
1200	0.002	−9.17×10−4	9.94×10−6	0.7980	1.04×10−3	−0.183	−0.99	2400
1200	0.003	−9.04×10−4	9.21×10−6	0.8063	9.59×10−4	−0.181	−0.99	2400
1200	0.005	−9.76×10−4	8.94×10−6	0.8205	9.31×10−4	−0.195	−0.99	2400
1200	0.01	−1.03×10−3	9.74×10−6	0.8337	1.01×10−3	−0.205	−0.99	2400
1200	0.03	−1.01×10−3	1.04×10−5	0.8477	1.09×10−3	−0.203	−0.99	2400
1200	0.05	−1.04×10−3	1.10×10−5	0.8522	1.15×10−3	−0.208	−0.99	2400
1200	0.07	−1.02×10−3	1.05×10−5	0.8554	1.09×10−3	−0.204	−0.99	2400
1200	0.09	−1.03×10−3	1.13×10−5	0.8586	1.18×10−3	−0.207	−0.99	2400
1500	0	−4.44×10−4	9.85×10−6	0.6953	1.03×10−3	−0.089	−0.94	2400
1500	0.001	−8.01×10−4	7.40×10−6	0.7924	7.71×10−4	−0.160	−0.99	2400
1500	0.002	−8.51×10−4	8.72×10−6	0.8129	9.07×10−4	−0.170	−0.99	2400
1500	0.003	−8.83×10−4	9.81×10−6	0.8197	1.02×10−3	−0.177	−0.98	2400
1500	0.005	−8.97×10−4	9.25×10−6	0.8296	9.62×10−4	−0.179	−0.99	2400
1500	0.03	−9.05×10−4	9.60×10−6	0.8515	9.99×10−4	−0.181	−0.99	2400
1500	0.05	−9.12×10−4	1.00×10−5	0.8561	1.04×10−3	−0.182	−0.99	2400
1500	0.07	−9.41×10−4	9.56×10−6	0.8585	9.95×10−4	−0.188	−0.99	2400
1500	0.09	−9.25×10−4	1.03×10−5	0.8599	1.07×10−3	−0.185	−0.98	2400

Table 4.

Results for a colonization rate of 0.13. (The columns contain, respectively, the carrying capacities of all demes, exchange rate, slope measured with respect to the total number of demes and its standard error, intercept and its standard error, total fall in heterozygosity from the origin to the deme farthest from the origin, correlation coefficient between average heterozygosity and geographical distance, and the total number of generations up to the end of the simulation.)

carrying capacity	exchange rate	slope	s.e.	intercept	s.e.	fall in heterozygosity	correlation coefficient	total generation
400	0	−2.13×10−4	2.16×10−5	0.4617	2.25×10−3	−0.042	−0.53	2200
400	0.003	−1.04×10−3	1.36×10−5	0.7210	1.42×10−3	−0.208	−0.98	2200
400	0.005	−1.10×10−3	1.25×10−5	0.7433	1.30×10−3	−0.219	−0.98	2200
400	0.01	−1.19×10−3	1.31×10−5	0.7720	1.36×10−3	−0.237	−0.99	2200
400	0.03	−1.26×10−3	1.23×10−5	0.8023	1.28×10−3	−0.252	−0.99	2200
400	0.05	−1.26×10−3	1.07×10−5	0.8142	1.12×10−3	−0.251	−0.99	2200
750	0	−2.53×10−4	1.39×10−5	0.5838	1.45×10−3	−0.051	−0.76	2200
750	0.002	−9.44×10−4	8.02×10−6	0.7589	8.35×10−4	−0.189	−0.99	2200
750	0.003	−1.01×10−3	8.19×10−6	0.7791	8.53×10−4	−0.201	−0.99	2200
750	0.005	−1.01×10−3	9.33×10−6	0.7881	9.72×10−4	−0.202	−0.99	2200
750	0.01	−1.08×10−3	1.01×10−5	0.8119	1.05×10−3	−0.215	−0.99	2200
750	0.03	−1.10×10−3	1.01×10−5	0.8353	1.05×10−3	−0.221	−0.99	2200
1000	0.001	−8.41×10−4	8.51×10−6	0.7740	8.86×10−4	−0.168	−0.99	2200
1200	0	−3.25×10−4	9.58×10−6	0.6636	9.97×10−4	−0.065	−0.91	2200
1200	0.001	−7.94×10−4	7.24×10−6	0.7808	7.53×10−4	−0.159	−0.99	2200
1200	0.002	−8.19×10−4	7.81×10−6	0.7982	8.13×10−4	−0.164	−0.99	2200
1200	0.003	−8.40×10−4	8.38×10−6	0.8063	8.72×10−4	−0.168	−0.99	2200
1200	0.005	−8.93×10−4	8.91×10−6	0.8209	9.27×10−4	−0.179	−0.99	2200
1200	0.01	−8.89×10−4	8.52×10−6	0.8328	8.87×10−4	−0.177	−0.99	2200
1500	0	−3.23×10−4	8.31×10−6	0.6951	8.65×10−4	−0.065	−0.93	2200
1500	0.001	−6.90×10−4	7.77×10−6	0.7920	8.09×10−4	−0.138	−0.99	2200
1500	0.002	−7.59×10−4	7.79×10−6	0.8133	8.11×10−4	−0.152	−0.99	2200
1500	0.003	−7.68×10−4	7.80×10−6	0.8185	8.12×10−4	−0.154	−0.99	2200
1500	0.005	−7.86×10−4	7.16×10−6	0.8266	7.45×10−4	−0.157	−0.99	2200
1500	0.01	−8.09×10−4	8.69×10−6	0.8396	9.04×10−4	−0.162	−0.99	2200

Table 5.

Results for a colonization rate of 0.18. (The columns contain, respectively, the carrying capacities of all demes, exchange rate, slope measured with respect to the total number of demes and its standard error, intercept and its standard error, total fall in heterozygosity from the origin to the deme farthest from the origin, correlation coefficient between average heterozygosity and geographical distance, and the total number of generations up to the end of the simulation.)

carrying capacity	exchange rate	slope	s.e.	intercept	s.e.	fall in heterozygosity	correlation coefficient	total generation
400	0	−2.09×10−4	2.19×10−5	0.4663	2.27×10−3	−0.040	−0.52	2000
400	0.004	−9.83×10−4	1.22×10−5	0.7166	1.27×10−3	−0.197	−0.98	2000
400	0.01	−1.13×10−3	1.10×10−5	0.7682	1.14×10−3	−0.226	−0.99	2000
400	0.03	−1.20×10−3	9.38×10−6	0.7999	9.77×10−4	−0.239	−0.99	2000
400	0.05	−1.23×10−3	9.40×10−6	0.8123	9.78×10−4	−0.246	−0.99	2000
400	0.09	−1.24×10−3	8.52×10−6	0.8245	8.87×10−4	−0.247	−0.99	2000
400	0.18	−1.25×10−3	9.41×10−6	0.8361	9.79×10−4	−0.249	−0.99	2000
750	0	−3.14×10−4	1.39×10−5	0.5887	1.45×10−3	−0.060	−0.82	2000
750	0.002	−8.30×10−4	8.57×10−6	0.7568	8.92×10−4	−0.166	−0.99	2000
750	0.003	−9.14×10−4	8.64×10−6	0.7768	8.99×10−4	−0.183	−0.99	2000
750	0.005	−9.22×10−4	8.04×10−6	0.7886	8.36×10−4	−0.184	−0.99	2000
750	0.03	−1.05×10−3	8.79×10−6	0.8320	9.15×10−4	−0.209	−0.99	2000
750	0.05	−1.05×10−3	7.64×10−6	0.8370	7.95×10−4	−0.211	−0.99	2000
750	0.18	−1.03×10−3	8.64×10−6	0.8504	8.99×10−4	−0.206	−0.99	2000
1000	0.001	−7.45×10−4	7.19×10−6	0.7741	7.48×10−4	−0.149	−0.99	2200
1200	0	−2.57×10−4	9.60×10−6	0.6638	9.99×10−4	−0.051	−0.86	2200
1200	0.001	−6.85×10−4	7.70×10−6	0.7827	8.01×10−4	−0.137	−0.99	2200
1200	0.002	−7.18×10−4	6.79×10−6	0.7977	7.07×10−4	−0.144	−0.99	2200
1200	0.003	−7.44×10−4	7.00×10−6	0.8060	7.29×10−4	−0.149	−0.99	2200
1200	0.005	−7.70×10−4	8.40×10−6	0.8222	8.75×10−4	−0.154	−0.99	2200
1200	0.01	−7.91×10−4	9.18×10−6	0.8334	9.55×10−4	−0.158	−0.98	2200
1500	0	−2.17×10−4	7.06×10−6	0.6931	7.35×10−4	−0.043	−0.89	2200
1500	0.001	−5.78×10−4	6.17×10−6	0.7904	6.42×10−4	−0.115	−0.99	2200
1500	0.002	−6.38×10−4	6.90×10−6	0.8111	7.18×10−4	−0.128	−0.99	2200
1500	0.003	−6.81×10−4	6.43×10−6	0.8182	6.69×10−4	−0.136	−0.99	2200
1500	0.004	−6.85×10−4	7.47×10−6	0.8249	7.77×10−4	−0.137	−0.99	2200
1500	0.01	−6.80×10−4	8.48×10−6	0.8375	8.83×10−4	−0.136	−0.98	2200
1500	0.03	−6.80×10−4	8.37×10−6	0.8497	8.71×10−4	−0.136	−0.98	2200
1500	0.05	7.06×10−4	9.10×10−6	0.8535	9.47×10−4	−0.141	−0.98	2200
1500	0.09	−7.48×10−4	9.41×10−6	0.8605	9.79×10−4	−0.150	−0.98	2200
1500	0.18	−7.08×10−4	9.63×10−6	0.8619	1.00×10−3	−0.142	−0.98	2200

Figure 1.

Plot of average heterozygosity with geographical distance from the origin of expansion. Carrying capacity of deme K=1000, colonization rate=0.13 and exchange rate among neighbouring demes=0.001. The correlation coefficient is −0.987. The intercept of the regression line is 0.774 and the total fall in heterozygosity is 0.16812. There are two boundary effects visible in the otherwise perfectly linear pattern. The boundary effect at a distance 50 from the origin of expansion is due to the populations near the left edge of the grid. The boundary effect at a distance close to 200 from the origin of expansion is due to the populations near the right edge of the grid. There is no boundary effect at the origin of expansion.

(a) Effect of varying the exchange rate

When we increase the exchange rate keeping the colonization rate and the carrying capacity fixed, the intercept of the regression line always increases. When the exchange rate is zero, the intercept is approximately as given by the formula $1-\sqrt{1+8Ku}$, where K is the carrying capacity of the deme and u is the stepwise mutation rate (0.0007567). This is the formula for the equilibrium heterozygosity for an isolated population given by Ohta & Kimura (1973) assuming a stepwise mutation model. The regression line is generally quite flat when there is no exchange between populations. But as soon as we allow even one member to be exchanged between each pair of neighbouring populations at every generation (Km=1), the intercept and the slope of the regression line are increased. This is probably because the values of Km (where m is the exchange rate) are generally higher than Ku. The values of Ku range from 0.3 (for a carrying capacity of 400) to 1.1 (for a carrying capacity of 1500). Therefore, adding even one migrant per generation has an effect equivalent to more than doubling the effective mutation rate, leading to a significant increase in the heterozygosity of the origin of expansion, and also the slope. The intercept and the slope keep increasing as we further increase the exchange rate. The values of the exchange rate of interest to us are those for which both the intercept and the slope fall within the range of values observed in the HGDP–CEPH microsatellite data. Once the intercept has increased to a sufficiently high value above 0.8, a further increase in the exchange rate may tend to slightly flatten the regression line, as the populations become more similar to one another with the large gene flow between them. It would be misleading to expect that an increase in the exchange rate should always homogenize the populations, and thereby flatten the regression line. One needs to take into account the effect of increasing the exchange rate on both the slope and the intercept, not just the slope. As long as an increase in the exchange rate increases the intercept sufficiently, the slope also increases. Our simulations revealed that the range of values for the exchange rate resulting in a slope and an intercept close to those obtained from the data is very narrow—the exchange rate is always less than 0.01 regardless of the carrying capacity or the colonization rate. This is much lower than the value for the rate suggested by Liu et al. (2006). They estimated that approximately 23 per cent of the individuals moved from one population to another (11.5% exchanged with each neighbouring population). This high value may, however, be due to confounding the colonization rate and the exchange rate (Liu et al. 2006). In general, there is no reason to suspect that rates of colonization and exchange should be the same. In most cases, mating would probably entail the woman moving to the place of the male. Colonization happens in groups, with a family or social unit moving into a new territory, and is more likely to occur when resources are in short supply (or when the deme is closer to saturation). This justifies separation of the two different forms of migration (colonization and exchange) instead of aggregating them under a single value.

(b) Effect of varying the colonization rate

If we keep the exchange rate below 0.01 (since it is for these values that the slope and intercept values are within the desired range) and decrease the colonization rate for a given carrying capacity, it does not have much effect on the intercept. But a decrease in the colonization rate tends to increase the magnitude of the fall in heterozygosity, i.e. it tends to make the regression line steeper. The smaller number of founders results in a larger amount of drift in the series of founder effects, which tends to decrease the successive heterozygosities by a greater amount. In our experiments, we varied the colonization rate from approximately 0.07 to approximately 0.4. A colonization rate that is too low would lead to a very slow occupation of the world. We kept the time since the origin of expansion of modern humans to between 50 and 60 Kyr. Assuming a generation time of approximately 25 years, this would make the number of generations since the expansion of modern humans between 2000 and 2400. A colonization rate that is too high would make the occupation of the world too rapid, and it would also be unrealistic to expect that, say, 40 per cent of the population at the wavefront are colonizers. Our experiments suggest that colonization rates between 0.09 and 0.18, combined with appropriate values for the carrying capacity of the demes, an exchange rate less than 0.01 and an acceptable time to complete the process, are most likely to result in the desired values of the slope and the intercept.

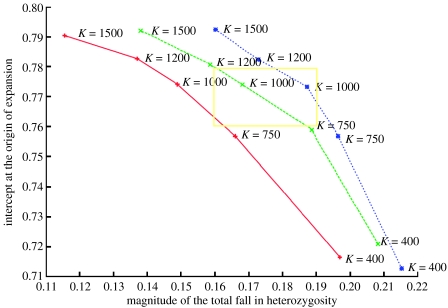
(c) Effect of varying the carrying capacity

Figure 2 shows the general pattern of variation of the slope–intercept values with the change in the carrying capacity. Each set of points connected by a curve corresponds to a particular colonization rate and a Km value of 1. The curves show that carrying capacity values between 750 and 1200 are most likely to produce a regression line close to the observed pattern. Actually, the results are more complex—the exact range for the carrying capacity depends on the colonization rate and the exchange rate. An increase in the carrying capacity tends to increase the intercept and decrease the magnitude of the fall in heterozygosity. By contrast, in the absence of continued exchange between the populations (i.e. with an exchange rate of zero), an increase in the carrying capacity increases the intercept and also the magnitude of the fall in heterozygosity. This reversal of the pattern is probably caused by the unequal change in the intercept when exchange is introduced. For example, in table 3, which shows the simulation results for a colonization rate of 0.09, with a carrying capacity of 400, the introduction of exchange pushes the intercept up from approximately 0.46 to 0.71. For a carrying capacity of 1500, the intercept goes up from approximately 0.70 to 0.79. Therefore, even though the regression line (without exchange) is steeper for the larger carrying capacity, the introduction of exchange actually makes it flatter.

Figure 2.

Plot of the magnitude of the total fall in heterozygosity versus the intercept of the regression line obtained for a set of experiments with Km=1. The area corresponding to the rectangle 0.16<x<0.19 and 0.76<y<0.78 represents values of the intercept and the slope for the regression line that are very close to the observed values for the data. The three sets of points shown are for three different colonization rates: 0.09 (blue dotted line); 0.13 (green dashed line); and 0.18 (red solid line). Starting from any point, an increase in the carrying capacity makes the point move in a top-left direction along the curve. An increase in the colonization rate makes the point move towards the left. An increase in the exchange rate makes the point move in the top-right direction. The exchange rate is always less than 0.01.

It is to be noted that our estimates of the carrying capacity would have been much higher if we had not allowed continued exchange of people between neighbouring populations. From tables 3–5, we note that the introduction of an exchange of just one migrant between neighbouring populations radically changes the regression line. Without this exchange, we would need to increase the carrying capacity of Africa to approximately 3000 to obtain an intercept compatible with the data. An exchange of one member every generation as a result of mating reduces the estimate of the carrying capacity by almost two-thirds, because the exchange rate and the mutation rate combined cause the intercept to increase. Thus, the drop in the intercept that would have been caused by the reduction in the carrying capacity is compensated by an increase in the exchange rate.

Liu et al. (2006) suggest that in their simulation model the expectations for average heterozygosities do not decrease linearly with geographical distance because the populations in the middle of the sequence have higher ‘effective neighbourhoods’. In our model, there is a departure from linearity only for a few populations near the edges of the grid, at a distance of approximately 50 demes to the left of the origin and 200 demes to the right of the origin (figure 1). The correlation coefficients between the average heterozygosity of a population and its geographical distance from the origin of expansion are always between −0.98 and −1 for the range of estimated parameters, strongly suggesting a linear relationship. There is no boundary effect near the origin of expansion. Since an origin somewhere in East Africa would allow for human migrations in multiple directions from the origin (as in our model), the use of linear regression on average heterozygosity provides a good estimate of the geographical origin of modern humans. Even in the model of Liu et al. (2006), the nonlinearity was not that strong, and a straight line was a good approximation for most of the range.

(d) Dimensionality and exchange

We have included both colonization and exchange subsequent to attainment of carrying capacity. The consequences of exchange are intimately related to the dimensionality problem. Using straightforward two-dimensional approaches, it proved very difficult to simulate a serial founder effect except with unrealistic demographic parameters, due to constraints of computer memory and time. Migration in the real world would be better represented by simulation with locally varying dimensionality that is intermediate between 1 and 2; this would, however, also involve much more computation than the present analysis. Moreover, choosing appropriate parameters for such a simulation is very difficult because the paths supposedly taken in past expansions are known only rather roughly. For example, sea travel is considered to have been important in the expansion to South Asia, but mainly along coasts that are now largely under the ocean, or along rivers that may have changed paths. Movement over land took place across areas with rivers, mountains and deserts that have changed with time in unknown ways.

The migration pattern out of Africa most probably involved a number of branches that occurred independently of one another. Our model of one-dimensional expansion can be viewed as an average of these independent trajectories (see fig. 2 of Liu et al. 2006). In reality, separation between the demes was sufficiently great that exchange rates must have been small.

The exchange rate between neighbours may also bias estimates from the data of another quantity: the carrying capacity. The simulations suggest that it is in the range of 600–1200. A recent estimate gave 839 as the average population size of hunter–gatherer populations (Hamilton et al. 2007), but it is not clear that this can be regarded as equivalent to a carrying capacity because the populations involved were estimated to be growing. Our simulation, however, uses discrete generations, and therefore our carrying capacity is that of only one generation in the simulation (i.e. approximately one-third that of the actual demographic population size, which includes, on average, approximately three generations). Therefore, the carrying capacity of the simulation should be multiplied by three to be comparable with demographic estimates of stable population size. Thus, the population size estimated from our simulation is two to four times higher than the above estimate from Hamilton et al. A possible explanation is that cultural evolution allowing increased carrying capacity continued over the tens of thousands of years during which the expansion from Africa took place.

5. Discussion

Our model incorporates essential features of earlier simulation models, and changes that improved the fit to the observed data. While the range of parameters we suggest represents the out-of-Africa migration of humans that took place 50–60 Kyr ago, the linear decay of heterozygosity with geographical distance from the origin of expansion could apply to the expansion of any species into a new geographical niche previously unavailable to it. Unlike previous models, ours separated colonization events from the continued exchange of people between occupied territories. Our estimates of the exchange rate between neighbouring populations were very low (below 0.01), with carrying capacities ranging from approximately 600 to 1200. Assuming that the census size is three times this effective population size, we derive a census size of approximately 1800–3600 people in each deme. Since each deme has dimensions of 125×125 km, this corresponds to a population density of approximately 0.11–0.23 persons km⁻², well within the range for hunter–gatherers referred to by Liu et al. (2006). The total time since the start of expansion was kept between 50 and 60 Kyr in conformance with archaeological dates. We assumed logistic growth because, as the population size of hunter–gatherers increases, the growth rate slows over time. This could happen owing to an increase in the death rate due to faecal contamination of a previously pristine environment, in addition to resource limitations (Cavalli-Sforza 1986). That we obtained a very high correlation of average heterozygosity with geographical distance from the origin, and no boundary effect at the origin, suggests that linear regressions are useful for estimating the geographical origin of modern humans. Theoretically, there are three parameters we vary: colonization rate; exchange rate; and carrying capacity. The exact range of variation for any parameter depends on the values of the other two parameters. For example, with a carrying capacity of 1200, we cannot increase the exchange rate above one person for every pair of neighbouring demes, and we cannot increase the colonization rate above 0.13. But with a lower carrying capacity of 600, we would need to increase the exchange rate and the colonization rate to find a good fit to the data. The exchange rate, however, always stays below 0.01. The close fit of our simulation results to the data suggests that our estimated parameters are not too far from the actual ethnographic parameters.

Very recently, the serial founder effect, originally observed for microsatellites, has been confirmed on the same set of DNAs but with 650 000 SNPs (Li et al. 2008)—or more exactly on haplotype frequencies derived from these SNPs. While the correlation of average heterozygosity and geographical distance was −0.87 with microsatellites, the same correlation with SNP haplotypes was −0.91. The slope of the fall in heterozygosity with geographical distance was definitely greater with haplotypes (−1.144×10⁻⁵), almost twice that observed with microsatellites (−0.652×10⁻⁵). This is expected because the intercepts of both regression lines are approximately the same and the mutation rate for SNPs is orders of magnitude smaller than for microsatellites. For the same intercept, higher mutation rates have the same effect as higher migration rates: they decrease this slope. Assessment of the effect on the slope of these different mutation rates is difficult, however, because the choice of haplotypes in the SNP data is biased towards SNPs of higher frequency.

The expansion model with the serial founder effect that has now been repeatedly validated may also apply to the expansion of other cosmopolitan invasive species with appropriate refinements to the parameters. It should be remembered, however, that the serial founder effect is not an equilibrium situation. Once the invasion of the available environment is complete, the resident population is continuously changed by both mutation and migration, which tend to eliminate the evidence of the founding. In the case of humans, when the whole world was almost completely settled, ca 10 Kyr ago, a major cultural set of innovations in food production, namely agriculture and animal breeding, initiated a new period of major population growth. To some extent, this growth reduced the effects of genetic drift, but it also introduced some new selective processes that had effects on some genes. The geographical pattern that was originally strongly influenced by drift will also be determined by local carrying capacities and their evolution. It is therefore likely that the regular, linear fall in heterozygosity in the direction of the expansion will disappear in the not too distant future.