Modeling the Drosophila melanogaster Circadian Oscillator via Phase Optimization

Abstract

The circadian clock, which coordinates daily physiological behaviors of most organisms, maintains endogenous (approximately 24 h) cycles and simultaneously synchronizes to the 24-h environment due to its inherent robustness to environmental perturbations coupled with a sensitivity to specific environmental stimuli. In this study, the authors develop a detailed mathematical model that characterizes the Drosophila melanogaster circadian network. This model incorporates the transcriptional regulation of period, time-less, vrille, PAR-domain protein 1, and clock gene and protein counterparts. The interlocked positive and negative feedback loops that arise from these clock components are described primarily through mass-action kinetics (with the exception of regulated gene expression) and without the use of explicit time delays. System parameters are estimated via a genetic algorithm-based optimization of a cost function that relies specifically on circadian phase behavior since amplitude measurements are often noisy and do not account for the unique entrainment features that define circadian oscillations. Resulting simulations of this 29-state ordinary differential equation model comply with fitted wild-type experimental data, demonstrating accurate free-running (23.24-h periodic) and entrained (24-h periodic) circadian dynamics. This model also predicts unfitted mutant phenotype behavior by illustrating short and long periodicity, robust oscillations, and arrhythmicity. This mechanistic model also predicts light-induced circadian phase resetting (as described by the phase-response curve) that are in line with experimental observations.

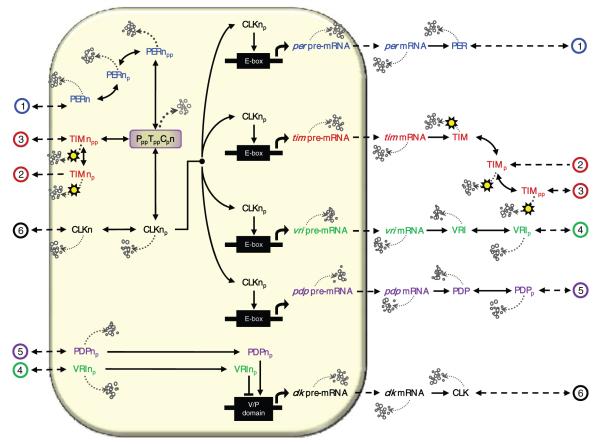
Biological systems are typically comprised of networks of interacting components. To elucidate the structure that gives rise to robust performance, biological experimentation and intuition are by themselves insufficient. The systematic development and analysis of biological models help guide further (arguably nonintuitive) experimentation and establish a premise from which researchers may adopt modules for the construction of synthetic biology or control the behavior of existing systems. An ideal system for this type of study is the circadian clock, which coordinates the daily physiological patterns of most organisms. The key gene/protein components that regulate Drosophila melanogaster circadian rhythms are period, timeless, vrille, PAR-domain protein 1, and clock³ (Allada et al., 1998; Bae et al., 1998; Darlington et al., 1998; Hardin et al., 1990; Kloss et al., 1998; Price et al., 1998; Rutila et al., 1998; Sehgal et al., 1994) as illustrated in Figure 1. Together, these components establish a complex transcriptional regulatory structure made up of both positive and negative feedback loops that describe the competitive activation and inhibition of gene expression.

Figure 1.

The Drosophila melanogaster circadian model. per-related components are labeled in blue, tim in red, vri in green, pdp in purple, and clk in black. The solid lined connectors represent complex cellular reactions, while the dashed connectors represent linear transport. Dotted lines denote relative degradation in which thicker lines imply greater degradation rates. The shaded box represents the nucleus; connectors that end at the far left or right of the figure are assumed to wrap around to the opposing side. For clarity, we assign numeric labels on these transport processes.

Two basic helix-loop-helix-PAS transcription factors, CLK and CYC, form heterodimers that bind canonical E-box sequences (CACGTG) to activate per, tim, vri, and pdp transcription around noon. per and tim mRNAs reach peak levels early in the evening, while their protein counterparts peak in the late evening (Allada et al., 1998; Bae et al., 1998; Benito et al., 2007; Blau and Young, 1999; Darlington et al., 1998; Edery et al., 1994; Glossop et al., 2003; Hao et al., 1997; Hardin, 2005; Lee et al., 1999; Myers et al., 1996; Rutila et al., 1998; Schoning and Staiger, 2005; Sehgal et al., 1995; Smolen et al., 2004; Zeng et al., 1996). This delay results most notably from the initial destabilization of PER through DBT-dependent phosphorylation; PER is stabilized via its dimerization with TIM (Glossop et al., 1999; Kloss et al., 1998). Although PER-TIM heterodimerization might be required for nuclear entry, TIM may be reexported during the early night (Shafer et al., 2002) and falls to low levels several hours before PER (Hardin, 2005; Nawathean and Rosbash, 2004). Once translocated to the nucleus, the PER-TIM complex can interact directly with the CLK-CYC complex to repress further per and tim transcription. The binding of nuclear PER-TIM to the CLK heterodimer prevents CLK’s binding to E-boxes (Bae et al., 2000; Blau and Young, 1999; Darlington et al., 1998; Glossop et al., 2003; Lee et al., 1999; Rothenfluh et al., 2000; Yu et al., 2006).

Once vri and pdp are expressed around noon, VRI then translocates to the nucleus where it peaks during the early night to repress the transcription of clk. Peak levels of PDP, however, occur 3 to 6 h after the peak of VRI and activate clk transcription in the middle of the night. VRI-dependent repression of clk leads to clk mRNA cycling that peaks shortly after dawn, which is anti-phase to maximum per, tim, vri, and pdp mRNA levels (which peak shortly after dusk) (Bae et al., 1998; Blau, 2003; Cyran et al., 2003; Darlington et al., 1998; Glossop et al., 1999, 2003; Hardin et al., 1990; Lee et al., 1998; Schoning and Staiger, 2005; Sehgal et al., 1994, 1995; Yu et al., 2006).⁴

Several mathematical models have been developed that aim to characterize the Drosophila melanogaster network underlying circadian rhythmicity (Leloup and Goldbeter, 1998; Kuczenski et al., 2007; Leise and Moin, 2007; Ruoff et al., 2005; olde Scheper et al., 1999; Smolen et al., 2004; Tyson et al., 1999; Ueda et al., 2001; Xie and Kulasiri, 2007). Recent experimental studies, however, provide additional molecular detail (unaccounted for in previous models) regarding complex network interactions. For instance, it was once thought that PER and TIM accumulate as heterodimers in the cytoplasm after a phosphorylation-dependent delay, then enter the nucleus simultaneously. This belief catalyzed the development of models that characterize period and timeless gene/ protein components as “redundant” loops,⁵ with the difference that light enhances degradation of phosphorylated TIM. It is now known that although the interaction of PER and TIM may stimulate nuclear localization of both proteins, it is not necessary for transport (Kim et al., 2007; Myers et al., 1996; Shafer et al., 2002). In fact, the lag between peak times of PER and TIM accumulation suggest that PER and TIM are not redundant and enter the nucleus separately (Cyran et al., 2005; Shafer et al., 2002). Experimental data further distinguish PER’s independence as it serves as a main repressor of CLK activity (Rothenfluh et al., 2000). Vital to the accurate modeling of circadian rhythms is the unique description of per and tim, and the use of nuclear versus cytoplasmic compartmentalization. Additional complexity derives from protein specific degradation. Studies suggest that phosphorylated proteins may be more readily targeted for degradation (Akten et al., 2003; Hardin, 2005; Kim et al., 2007; Ko et al., 2002; Lin et al., 2002; Schoning and Staiger, 2005), encouraging the explicit modeling of proteins (and their corresponding degradation rates) with respect to their phosphorylated states. Furthermore, experimental studies highlight phase (not period) as a key characteristic of circadian performance, since exact periodicity of circadian rhythms is not critical to the clock’s ability to entrain to external time through environmental factors (Dunlap et al., 2004; Daan and Pittendrigh, 1976). Thus, unlike previous modeling efforts that focus on amplitude and period behavior, the strict phase behavior that defines circadian rhythms warrants its use in the development and analysis of circadian models.

In this study, we develop a detailed deterministic mathematical model of the Drosophila melanogaster circadian network that incorporates the transcriptional regulation of per, tim, vri, pdp, and clk genes and protein counterparts in addition to phosphorylation and nuclear/cytoplasmic localization. The positive and negative feedback loops that arise from these interlocked clock components are described primarily through mass-action kinetics (with the exception of mRNA transcription) and without the use of explicit time delays.

MATERIALS AND METHODS

Through the use of mass-action and Hill-type kinetics, we develop a 29-state Drosophila melanogaster circadian model that, based on current circadian literature, most appropriately defines the Drosophila melanogaster clock. We do not consider individual stochastic effects and thus consolidate many complex cellular processes into a single deterministic equation. Although gene expression, for instance, is modeled as a single all-inclusive event that gives rise to pre-mRNA, it is important to note that this single process includes the binding of an activator, initiation, elongation, and so on. Such (arguably stochastic) details are assumed to be lumped into the system’s 84 parameters that describe rates relating to transcription, translation, phosphorylation, association, transport, and degradation. We reduce the parameter search space to 36 dimensions by grouping gene/protein-specific terms into a single variable; for instance, we set all mRNA degradation rates equal. Through use of an evolutionary strategy, we estimate the 36 unique parameters according to a collection of phase-based performance criteria that quantify the “fitness” of the model. The predictive power of the resulting model is assessed through the simulation of mutant phenotype behavior in addition to the model’s phase response with respect to changes in simulated environmental light.

Model Structure

A visual representation of the network is shown in Figure 1; details describing state variables, system parameters, and kinetics are outlined in the supplementary material (available at http://jbr.sagepub.com/supplemental/).

Gene Expression, mRNA Transcription, and Protein Translation

We use Hill-type kinetics (an expression commonly used to describe the transcription of circadian components [Leloup and Goldbeter, 1998; Ueda et al., 2001]) to characterize CLK-induced gene transcription⁶: $\frac{d[\ast n]}{dt}={\alpha }_{c\ast }\cdot \frac{{\left[\mathit{CLK}\mathit{pn}\right]}^{\mathit{hc}\ast }}{K_{\mathit{ca}\ast }^{\mathit{hc}\ast }+{\left[\mathit{CLK}\mathit{pn}\right]}^{\mathit{hc}\ast }}-{\beta }_{\ast }[\ast n]-{\delta }_{m\ast }[\ast n]$ This equation is general and may be applied to per, tim, vri, or pdp expression by specifying the state variable, *. System parameters also provide a means to customize these kinetics with respect to the circadian component or process: α_c* is the maximal nuclear phosphorylated CLK protein activated transcription rate; hc* is the nuclear phosphorylated CLK protein activated Hill coefficient; K_ca* is the Michaelis-Menten constant for nuclear phosphorylated CLK protein activation of [*n] expression; β_* is the irreversible transport rate of nuclear pre-mRNA to cytoplasmic mRNA; and δ_m* is the corresponding degradation rate.

The equation describing clk transcription is similar to the Hill-based kinetics described above since PDP activates its expression. VRI, however, competes with PDP to bind to the same site on the clk promoter and inhibit its expression. We characterize these dynamics through the multiplication of 2 Hill-type equations that are specific to activation and inhibition: $\frac{d\left[\mathit{clkn}\right]}{dt}={\alpha }_{\mathit{dc}}\cdot \frac{{\left[\mathit{PDP}\mathit{pn}\right]}^{\mathit{hdc}}}{K_{\mathit{dac}}^{\mathit{hdc}}+{\left[\mathit{PDP}\mathit{pn}\right]}^{\mathit{hdc}}}\cdot \frac{K_{\mathit{vic}}^{\mathit{hvc}}}{K_{\mathit{vic}}^{\mathit{hvc}}+{\left[\mathit{VRI}\mathit{pn}\right]}^{\mathit{hvc}}}-{\beta }_c\left[\mathit{clkn}\right]-{\delta }_{\mathit{mc}}\left[\mathit{clkn}\right]$. When nuclear levels of VRI are high, the transcription of clk is low since the overall maximal production rate, α_dc, is multiplied by a value close to 0. Once levels of VRI decrease and PDP peaks, the production rate is resecured as it is multiplied by a value close to 1.

Gene expression occurs in the nucleus (the shaded region in Fig. 1) and is displayed by an arrow for activation, or a blunt edge for inhibition. Nuclear pre-mRNA is either irreversibly degraded or transported to the cytoplasm, where it is irreversibly translated into its protein counterparts (PER, TIM, VRI, PDP, and CLK). The reactions describing transport, degradation, and translation are defined by linear mass-action kinetics.

Phosphorylation, Transport, and Dimerization

DBT, SGG, and CK2 are assumed to modulate the phosphorylation and stability of PER and TIM in both the cytoplasm and the nucleus (Akten et al., 2003; Cyran et al., 2005; Hardin, 2005; Kloss et al., 2001; Lin et al., 2002; Price et al., 1998; Meyer et al., 2006; Nawathean and Rosbash, 2004; Shafer et al., 2002). Since they are expressed constitutively (Schoning and Staiger, 2005), DBT, SGG, and CK2 are not explicitly modeled as individual states; instead, their phosphorylation effects are assumed to be contained in the parameters.

Experimental data point to a lag between peak nuclear PER and TIM accumulation that may be due to the proteins’ phosphorylation effects. Phosphorylated PER is prevented from shuttling back into the cytoplasm, whereas unphosphorylated PER undergoes nuclear import and export (Nawathean and Rosbash, 2004; Schoning and Staiger, 2005). As a result, we do not model phosphorylated cytoplasmic PER because evidence suggests that it does not directly affect circadian gene regulation. We do, however, model its phosphorylation in the nucleus since it binds to hyperphosphorylated TIM and CLK to form the complex P_ppT_ppC_pn (Fig. 1). Given that DBT enters a complex containing CLK at times when CLK becomes hyperphosphorylated, DBT may also act to phosphorylate CLK (Yu et al., 2006). Thus, CLK phosphorylation dynamics are assumed to follow similar principles as those describing PER phosphorylation.

TIM nuclear entry is permitted once the protein is hyperphosphorylated. All phosphorylated forms of nuclear TIM, however, translocate back to the cytoplasm (Meyer et al., 2006), supporting a nucleus-to-cytoplasm transport that operates in a single direction (Fig. 1). Although experimental data support the formation of a cytoplasmic PER-TIM complex, we ignore their corresponding heterodimers; the transport of their individual proteins occurs on a faster (more prominent) time scale than the transport of their complex, lending the heterodimer less influential in regulating gene expression. While the mechanisms driving VRI, PDP, and CLK phosphorylation are still unclear, we consider their phosphorylated states and model them assuming that their respective phosphorylating proteins are abundant and constitutively expressed (just as DBT, SGG, and CK2).

Feedback Regulation

The binding of a hyperphosphorylated form of PER to CLK may cause ubiquitination through SLIMB and subsequent degradation of the whole complex (Schoning and Staiger, 2005), preventing nuclear CLK from activating gene expression. Hypophosphorylated PER, however, is described to be a poor repressor (Nawathean and Rosbash, 2004), indicating that the stable association of PER with CLK is not fully sufficient to block transcription; PER-CLK heterodimers are thereby not considered in the model. The synergistic repression of CLK activity via PER and TIM, however, is considered. Nuclear PER and TIM indirectly repress their gene expression by binding to CLK to form the complex P_ppT_ppC_pn (Fig. 1), preventing CLK’s binding to E-boxes. Nuclear VRI is also considered to establish a circadian inhibition mechanism since it competes with PDP to bind to the clk promoter sequence and inhibit its expression.

Light

The major entraining cue for circadian rhythms is light, which causes rapid TIM protein degradation (Blau and Young, 1999; Hunter-Ensor et al., 1996; Myers et al., 1996; Zeng et al., 1996): Photoreceptors trigger the ubiquitin-proteasome dependent degradation of TIM via tyrosine phosphorylation (Hardin, 2005). In this model, light effects are taken into account in multiple kinetic equations via an additive input, l, that magnifies TIM protein degradation rates. Light-enhanced degradation of TIM proteins is described by the overlaid sun in Figure 1.

Parameter Estimation

As is the case for many biological systems, the few experimental data that exist are sparse, noisy, and varied. As a result, researchers have not been able to identify experimental values that define parameters specific to circadian rhythms. Parameters specific to the circadian system may include rates of gene expression, translation, phosphorylation, and similar. To overcome these challenges, we employ a parameter estimation algorithm that makes use of a cost function that quantifies the agreement between our model and key experimental results, namely, phase dynamics. A stochastic optimizer that mimics survival of the fittest (as seen in natural evolution) is employed. This genetic algorithm is defined by the process of selection (via the cost function, where a lower cost implies better fitness), random recombination, normally distributed mutation, and fitness evaluation. Such population-based algorithms are designed to avoid local minima, increasing the likelihood of obtaining an optimal solution. We have provided details outlining the optimization strategy and parameter estimation in the supplementary material.

Cost Function

The cost function serves to quantify model accuracy by measuring parameter-dependent deviations between model behavior and experimental observations with a relative weight, or penalty, assigned to the corresponding error. In this work, the cost is defined by the sum of squares, ensuring both non-negative components and a quadratic penalty. We perform three sequential optimization procedures (using three unique cost functions), where the resulting children from one optimization serve as the parents for the next optimization.

The first employed cost function dictates that the free-running system be oscillatory and consist of positively valued states, and are subsequently assigned a cost reflecting the circadian accuracy of its free-running period, τ_dd(x(t, p)), where x(t, p) describes the system’s 29-state output dynamics as a function of both time, t, and the estimated 36-length parameter vector, p. The scalar cost value is thereby defined as J₁(x(t, p)) = (24—t_dd(x(t, p)))². For simplicity we use τ_dd in place of τ_dd(x(t, p)).

Evolution of parameter sets is then directed by the weighted sum of seven fitness sub-functions, C_2i(x(t,p)), that make up the second cost function $J_2\left(\mathrm{x}\right(t,\mathrm{p}\left)\right)={\Sigma }_{i=1}^7{C}_{2i}\left(\mathrm{x}\right(t,\mathrm{p}\left)\right)$. Since the scaling of parameters provides a means of tuning the period of oscillation, we concentrate on obtaining proper phase relationships among circadian components. Hence, amplitude and period dynamics are weighted less (by a factor of 1 or 10), while general phase dynamics between PER and TIM are weighted more (by a factor of 20), and phase dynamics fundamental to feedback regulation, or those concerning CLK activity, are weighted most (by a factor of 30).

1. The system’s free-running period is weighted by 10: C_2,1(x(t, p)) = 10.(24—τ_dd)².

2. The transcription of per, tim, vri, and pdp occurs in phase, thus C_2,2(x(t, p)) = 20(T_pt)² + 20 (T_pv)² + 20 (T_pd)² + 10 (T_PT)², where T_** reflects the time difference between peak per and tim (pt), per and vri (pv), per and pdp (pd), and PER and TIM (PT) concentrations.⁷ The difference in weights accounts for the possibility that although PER and TIM phase dynamics are hypothesized to be the same in a free-running environment, their protein dynamics may not be identical since they enter the nucleus, (de)phosphorylate, and (dis)associate at different points of their cycle.

3. Experimental data suggest that PER and TIM proteins peak approximately 6 h ($\sim \frac{1}{4}$ of the endogenous cycle) after their respective mRNAs. Hence, $C_{2,3}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)=10\cdot {\left(T_{pP}-\frac{{\tau }_{\mathit{dd}}}{4}\right)}^2$ where T_pP reflects reflects the time difference between peak per mRNA and protein concentrations.

4. Another criterion vital to circadian phase dynamics requires that clk mRNA oscillate antiphase to per, tim, vri, and pdp mRNA. Thus, we penalize the time interval between peak per and clk mRNA concentrations, $T_{\mathit{pc}}:C_{2,4}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)=30\cdot {\left(T_{\mathit{pc}}-\frac{{\tau }_{\mathit{dd}}}{2}\right)}^2$

5. Precise clk mRNA regulation depends on the timing of nuclear VRI and PDP; nuclear PDP peaks 3 to 6 h after nuclear VRI. This time interval reflects approximately $\frac{1}{5}$ of the endogenous cycle. Hence, $C_{2,5}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)=30\cdot {\left(T_{\mathit{DV}n}-\frac{{\tau }_{\mathit{dd}}}{5}\right)}^2$, where T_DVn denotes the time difference between peak nuclear PDP and VRI protein concentrations.

6. Although establishing experimentally accurate phase dynamics is the aim of our parameter estimation, certain amplitude characteristics are considered and weighted with a minimal penalty of 1. One such criterion suggests that nuclear CLK, VRI, and PDP should have similar amplitude. Thus, we define the cost as C_2,6 (x(t,p)) = 1 (Δ_CP)² + 1 (Δ_CV)² + (Δ_DV)², where Δ** denotes the peak concentration difference between CLK and PER (CP), CLK and VRI (CV), and PDP and VRI (DV).

7. A similar criterion mandates that peak CLK protein levels, Λ_C, be several-fold lower than that of PER (or TIM), Λ_P. Here, we interpret “several-fold lower” as approximately “5 times lower”: $C_{2,7}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)=10\cdot {\left(\frac{{\Lambda }_P}{{\Lambda }_C}-5\right)}^2$.

Once a set of children parameter sets exhibit reasonable free-running behavior, we re-run the genetic algorithm with a modified cost function, J₃ (x(t, p)), where C_{3, 1} (x(t, p)) includes a penalty for light/dark dynamics via the light/dark entrained period, τ_ld. Knowing that the free-running period of oscillation is often described as a distribution of values less than 24 h, we quantify the endogenous period error with respect to 23.5 h. This value, however, is flexible. An additional entrainment-dependent cost, C_{3, 8} (x(t, p)), suggests that TIM proteins fall to low levels several hours before PER when subject to light/dark cycles, $C_{3,8}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)=20\cdot {\left(T_{\mathit{PT}}-\frac{{\tau }_{\mathit{ld}}}{4}\right)}^2$ Due to the additional consideration of circadian light/dark dynamics, the weights defining entrainment are of highest priority and weighted by a factor of 200.

$$\begin{array}{cc}\hfill C_{3,1}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)& =40\cdot {(23.5-{\tau }_{\mathit{dd}})}^2+200\cdot {(24-{\tau }_{\mathit{ld}})}^2\hfill \\ \hfill C_{3,2}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)& =40\cdot {\left(T_{\mathit{pt}}\right)}^2+40\cdot {\left(T_{\mathit{pv}}\right)}^2+40\cdot {\left(T_{\mathit{pd}}\right)}^2+20\cdot {\left(T_{\mathit{PT}}\right)}^2,\hfill \\ \hfill C_{3,3}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)& =20\cdot {\left(T_{pP}-\frac{{\tau }_{\mathit{dd}}}{4}\right)}^2,\hfill \\ \hfill C_{3,4}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)& =40\cdot {\left(T_{\mathit{pc}}-\frac{{\tau }_{\mathit{dd}}}{2}\right)}^2,\hfill \\ \hfill C_{3,5}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)& =40\cdot {\left(T_{\mathit{DV}n}-\frac{{\tau }_{\mathit{dd}}}{5}\right)}^2,\hfill \\ \hfill C_{3,6}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)& =1\cdot {\left({\Delta }_{\mathit{CP}}\right)}^2+1\cdot {\left({\Delta }_{\mathit{CV}}\right)}^2+1\cdot {\left({\Delta }_{\mathit{DV}}\right)}^2,\hfill \\ \hfill C_{3,7}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)& =10\cdot {\left(\frac{{\Lambda }_P}{{\Lambda }_C}-5\right)}^2,\hfill \\ \hfill C_{3,8}\left(\mathbf{x}\right(t,\mathbf{p}\left)\right)& =20\cdot {\left(T_{\mathit{PT}}-\frac{{\tau }_{\mathit{ld}}}{4}\right)}^2.\hfill \end{array}$$

RESULTS

Endogenous Rhythms

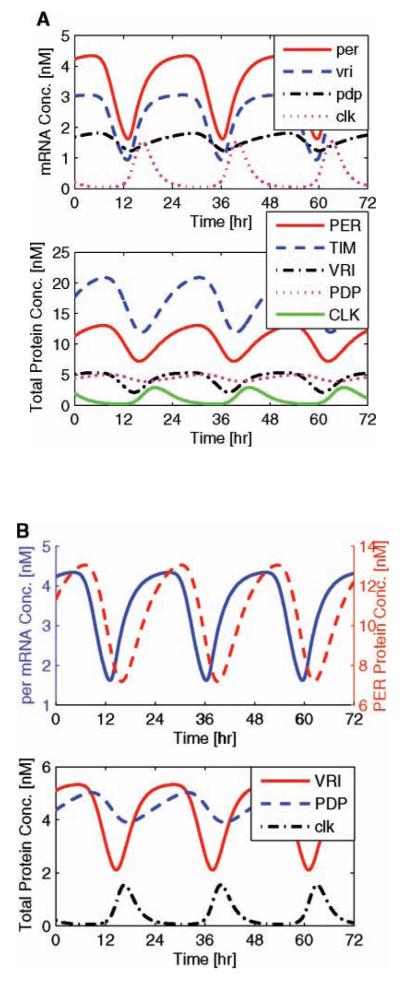
Given that the cost function is designed to fit parameters according to several wild-type free-running circadian attributes, we expect that the resulting system conforms to these prescribed rules. In Figure 2, we portray the experimentally justified dynamics of endogenous circadian rhythms that oscillate with a period of 23.24 h. The mRNA trajectories of this system are described in the upper plot, while their total protein dynamics are described in the lower plot. As expected, per, tim, vri, and pdp mRNA concentrations oscillate in phase, while clk-related trajectories peak nearly antiphase (with a phase difference of 10.9 hours). In dark/dark, per and tim prove to have identical phase and comparable amplitude dynamics; in Figure 2a, upper plot, their mRNA trajectories superimpose.

Figure 2.

Endogenous circadian rhythms. Simulated free-running circadian rhythms exhibit experimentally justified phase dynamics. In the upper subplot of (a), mRNA trajectories confirm that all circadian components are in phase (with the exception of clk, which is antiphase), while the lower subplot shows their total protein dynamics. Panel (b) depicts the accurate timing between mRNA and protein (∼3 h) (upper plot), and between clk-inhibiting VRI and clk-activating PDP (3.4 h) (lower plot).

The timing of protein translation corresponds to experimental data as the time interval between peak mRNA and cytoplasmic protein is approximately 2.9 h (Fig. 2b, upper plot). Critical to clk mRNA regulation, vri and pdp mRNA trajectories oscillate in phase, while their nuclear protein trajectories oscillate with a 3.3-h phase difference (Fig. 2b, lower plot), switching between positive and negative feedback.

Phase-Response Curve

In addition to complying with wild-type dynamics, the presented model meets the qualitative (and to a degree, the quantitative) phase response of the Drosophila melanogaster organism according to the phase-response curve (PRC) (Fig. 3). This curve maps the circadian time of the entraining stimulus (3-h pulses of light) against the resulting change in phase of an organism’s behavior while kept in a free-running environment. If the perturbed rhythm leads the nominal rhythm by less than one-half cycle upon admission of a light pulse, there exists a phase advance (denoted by a positive phase difference); or, if it lags by less than one-half cycle, a phase delay (denoted by a negative phase difference) (Winfree, 2001). In Drosophila melanogaster, a 3-h pulse of light has shown to induce up to 3.6 h of phase advance and 4.2 h of phase delay (Leloup and Goldbeter, 1998). Although the model does not account for the precise phase-resetting values depicted in the study by Leloup and Goldbeter (1998), the maximum phase advance and delay produced by the simulations are on the same order of magnitude as those observed in experimental data. In particular, we demonstrate a maximum phase advance of ∼1 h with a maximum delay of ∼0.6 h. As with many biological observations, these phaseresetting data include large experimental error (noise) (Konopka et al., 1991), prioritizing the ability to characterize qualitative phase-response behavior over quantitative values.⁸ The desired dead zone is achieved through use of a state-based gating function. This function, G(t), secures a 9-h dead zone while maintaining accurate endogenous state dynamics by modulating the light input.

Figure 3.

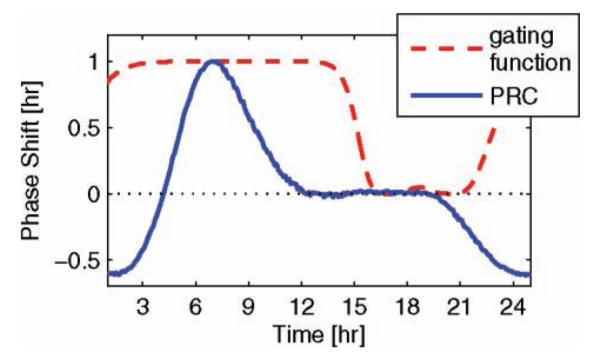
Gated circadian phase response. The x axis reflects time at which a 3-h pulse of light is applied to the model (via an additive light input), while the y axis reflects the resulting phase shift; a positive shift denotes an advance. The pulses of light are gated through use of a state-based gating function that decreases the effect of light during the subjective day. The output of this gating function is depicted by the red dash-dot line.

Gating functions have been used effectively in mammalian circadian models to produce accurate PRCs in a free-running (dark/dark) environment (Geier et al., 2005). As with Geier et al., we heuristically produced a state-based gating function (defined in the supplementary material) and multiply its output to the additive light input. This clk mRNA and protein concentration dependent function switches between 0 (during the subjective day) and 1 (during the subjective night), negating the effects of light between CT16 and CT21 (Fig. 3).

Entrained Rhythms

Experimental studies suggest that light increases TIM protein degradation rates (Hunter-Ensor et al., 1996; Myers et al., 1996; Smolen et al., 2004; Zeng et al., 1996). Although each child parameter set reflects some form of light entrainment, we regard the 1 with greatest accuracy (or lowest cost J₃(x(t, p))), whose free-running period, τ_dd, is less than 24 h and entrained period, τ_ld, is exactly 24 h. Light is thereby modeled as an additive input magnifying the degradation of all TIM proteins. More specifically, this environmental light input (that doubles TIM degradation rates) entrains a free-running 23.24-h period to 24.00 h, forcing a 0.76-h change in periodicity. In Figure 4, we simulate circadian entrainment as a function of regular 24-h light/dark cycles (depicted as gray square waves), where the upper plot describes entrained mRNA concentrations as a function of circadian time,⁹ and the lower plot describes the corresponding total protein concentrations. This figure confirms the accurate phase dynamics among mRNA and protein concentration profiles.

Figure 4.

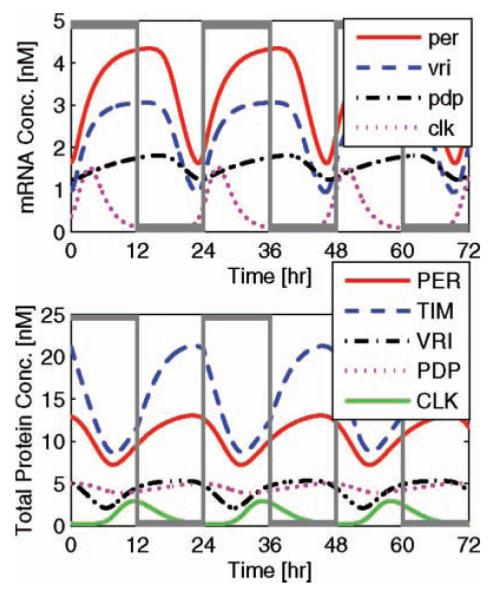
Entrained circadian rhythms. Entrainment of the simulated free-running circadian rhythms by light/dark cycles (gray square waves) results in exact 24-h oscillations. The magnitude of the light input (nominally 2) is magnified to span the height of the figure, illustrating the onset of 12-h day/night cycles. Light-entrained mRNA trajectories (upper plot) demonstrate consistent and experimentally accurate phase dynamics, while their total protein dynamics (lower plot) characterize light-induced amplitude and phase resetting via TIM (described by a blue dashed line).

It is important to note that day length may not be exactly 12 h; it might be longer in the summer and shorter in the winter. Our model accounts for irregular distributions of light throughout the 24-h day. In Figure 5, we illustrate robust entrainment of circadian dynamics as they entrain to a 24-h day via 16 h of lights-on (8 h off), 12 h of lights-on (12 h off), and 8 h of lights-on (16 h off). Light/dark cycles are illustrated by the square wave on the bottom half of the plot. The magnitude of light has been modified to better illustrate the onset of day and night. The system’s robustness to variations in day length is a quality not accounted for in parameter estimation; it is a model prediction, unfitted to experimental data.

Figure 5.

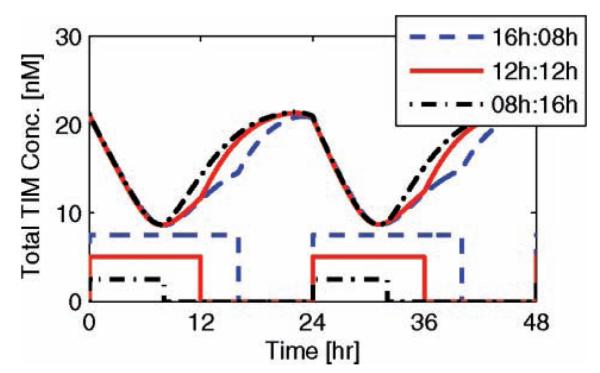
Entrainment of circadian rhythms via irregular (or seasonal) light/dark cycles. The red solid lines illustrate circadian entrainment through 16-h days and 8-h nights, the blue dashed lines illustrate regular 12-h light/dark cycles, and the black dot-dashed lines illustrate 8-h days and 16-h nights. The upper curve reflects total TIM concentration levels while the lower square wave reflects the onset of light. The magnitudes of these square waves are modified for visual clarity; the light input for each individual entrainment is equivalent.

Mutant (In)Validation

Vital to the understanding of biological systems is characterizing both wild-type and mutant behavior. In particular, we focus on mutations that affect the period, phase, or existence of oscillations and ignore amplitude effects whose measurements are often biased by experimental noise. For instance, an increase in per mRNA levels, or reducing vri gene dosage, causes period shortening (Baylies et al., 1987; Blau and Young, 1999). We simulate the former in Figure 6 (upper plot) by doubling and quadrupling the transcription rate of per mRNA, which results in free-running periods of 22.95 h and 22.83 h, respectively. Similarly, when the transcription rate of vri is decreased to 90% of its original value, we observe a simulated free-running period of 20.8 h. There are no significant changes to the entrained period of oscillation since the periods of mutant phenotypes are corrected by 24-h light/dark cycles.

Figure 6.

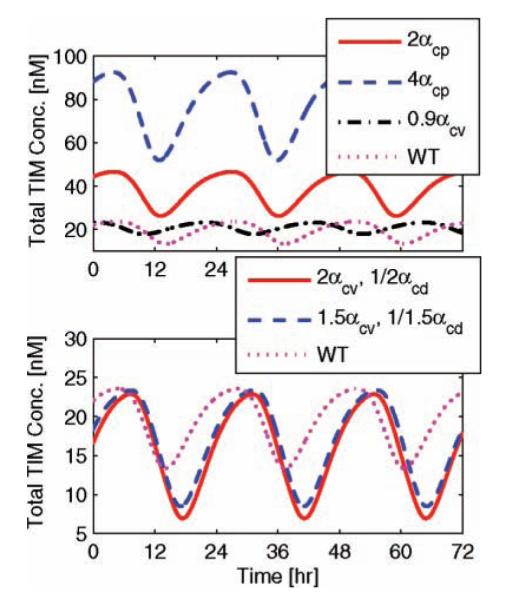
Mutant phenotype behavior. The predictive quality of the circadian model is confirmed via the implementation of mutant phenotype data. Here we plot the total TIM protein concentration as a function of time, 3 days after the mutation is enabled. Wild-type (WT) behavior is depicted by the magenta dotted lines. The upper plot describes how increasing per transcription rates by a factor of 2 and 4, or decreasing vri transcription rates by 10%, reduces the free-running period from 23.24 h to 22.95, 22.83, and 20.8 h, respectively. The lower plot investigates the mutual effect of increasing vri production while decreasing pdp. When their transcription rates are magnified/reduced by a factor of 1.5, the free-running period lengthens to 23.93 h; a mutation corresponding to a factor of 2 yields a period of 23.77 h.

Conversely, overexpression of vri combined with reduced pdp levels synergistically increase period length (Blau, 2003; Cyran et al., 2003). We simulated this phenotype by multiplying the transcription rate of vri by a factor of 1.5 and 2, while dividing the transcription rate of pdp by 1.5 and 2 (Fig. 6, lower plot). These simultaneous perturbations result in free-running periods of 23.93 h (relating to the magnification/reduction by a factor of 1.5) and 23.77 h (relating to a factor of 2).

Additional mutant experimentation demonstrates that the reduction of PDP levels by ∼70%, or the augmentation of PDP levels by ∼10-fold in clock cells does not alter clk mRNA cycling or circadian oscillator function (Benito et al., 2007). These clock phenotypes were implemented in the model by running a series of simulations, wherein we perturb each pdp-related state independently by multiplying its trajectories by a factor of 0.3 or 10. The simulated disturbances had no effect on the clock’s period. Even further, constant low or high PDP levels do not disrupt clk mRNA cycling or oscillator function (Benito et al., 2007). Constitutively expressed pdp was investigated by setting every respective state to a constant low, average, and high concentration value. In each case, the system proves to be robust to these state perturbations, maintaining nominal 24-h rhythmicity. When levels of VRI or CLK are held constant, however, the system results in arrhythmia, contradicting the argument that 2 feedback loops involving clk are not essential for oscillations (Smolen et al., 2004). Arrhythmia resulting from constitutively expressed VRI agrees with the experimental findings of Blau and Young (1999) and the analysis provided by Cyran et al. (2003).

Arrythmia is also observed in mutants that do not produce functional PER (per01), TIM (tim0), or CLK (CLK-jrk) (Bae et al., 1998; Glossop et al., 1999; Konopka and Benzer, 1971; Sehgal et al., 1994; Smolen et al., 2004). We simulate the per01 and tim0 mutants by setting their nuclear protein association rates to 0, preventing their binding to nuclear CLK. Simulations of these mutants do not comply with the experimental evidence that results in arrhythmia (Bae et al., 1998; Glossop et al., 1999; Konopka and Benzer, 1971; Sehgal et al., 1994; Smolen et al., 2004); although states relating to PER and TIM decrease in amplitude, VRI and PDP maintain nominal rhythmicity. Ruoff et al. (2005), however, introduce other reports that suggest the existence of oscillations in fly strains that lack functional per. Due to these contradicting data, we do not consider the per01 mutant phenotype essential to our model because of the need for further investigations. Dysfunctional CLK, or CLK-jrk, is simulated by setting all nuclear CLK-related Hill coefficients to 0. Our results corroborate experimental findings; CLK-jrk abolishes rhythmicity. Further mutant phenotypes that affect amplitude dynamics while maintaining nominal phase behavior are not evaluated in this study, since circadian phase performance is the primary focus of model development and analysis. A summary of wild-type and mutant phenotype behavior is outlined in Table 1.

Table 1.

Comparison of model structure and accuracy with respect to experimental observations for wild-type and mutant phenotypes.

	Bagheri et al. (2008)	Kuczenski et al. (2007)	Leise & Moin (2007)	Leloup & Goldbeter (1998)	Ruoff et al. (2005)	Smolen et al. (2004)	Ueda et al. (2001)	Xie & Kulasiri (2007)
Structure
Mirrored PER and TIM	No	Yes	Yes	Yes	Yes	Yes	Yes	Yes
Includes phosphorylation	Yes	Yes	No	Yes	No	Yes	No	No
Includes compartmentalization	Yes	Yes	Yes	Yes	Yes	Yes	Yes	No
Wild type
Free-running τ (h)	23.24	23.8	23.9	24.1	21.2	24	24	24
mRNA to protein phase (h)	3	3.5	7	2	n/a	5	3.8	n/a
CLK to PEr phase (h)	11	4	6	n/a	7	2	8	11
VRI to PBP phase (h)	3	2	n/a	n/a	6.5	3	n/a	6
PRC
Maximum phase advance (h)	1	—	3.5	3	—	2	0.3–3.2 a	2
Maximum phase delay (h)	0.6	—	3.5	4.5	—	4	0.3-2.2 a	4
Duration of dead zone (h)	9	—	6	12	—	10	8	6
Mutant
per overexpression	Short τ	Short τ	—	—	Short τ	Short τ	—	—
vri underexpression	Short τ	—	—	—	Short τ	Short τ	—	—
vri over- & pdp underexpression	Long τ	—	—	—	—	Long τ	—	—
Low PDP levels	Nominal	—	—	—	—	—	—	—
High PDP levels	Nominal	—	—	—	—	—	—	—
Consecutive PDP	Nominal	—	—	—	—	Nominal	—	—
CLK-jrk	Arrythmic	Arrythmic	—	—	—	Arrythmic	Arrythmic	Arrythmic
per 01 or tim 0	Nominal	Arrythmic	Arrythmic	—	—	Arrythmic	Arrythmic	Arrythmic

NOTE: The circadian behavior corresponding to several Drosophila melanogaster models is outlined. Each row outlines a circadian quality relating to the structure of the model, or wild-type and mutant phenotype behavior. Each column reflects dynamics specific to a published model. The boldface data reflect experimentally accurate attributes. The empty cells denote data not addressed in the development of the model.

^aThe maximum phase advance/delay specific to the Ueda et al. (2001) model depends on the magnitude of the light input as it varies between the 2- and 10-fold for the duration of 1 h.

DISCUSSION

We introduce a Drosophila melanogaster circadian model that characterizes fitted experimental data and predicts unfitted mutant phenotype behavior. Our model is unique since other researchers exclude clk regulation via vri and pdp (Leise and Moin, 2007; Leloup and Goldbeter, 2000; olde Scheper et al., 1999; Tyson et al., 1999; Ueda et al., 2001) or lump per and tim into a single state (olde Scheper et al., 1999; Smolen et al., 2004; Tyson et al., 1999; Ruoff et al., 2005).

We characterize per and tim as independent entities, discouraging redundancy since it is important to address the opposing tendencies of unmodified PER to enter the nucleus and of unmodified TIM to accumulate in the cytoplasm (Cyran et al., 2005); the unique timing of their nuclear entry may provide further insight regarding circadian performance. We include compartmentalization by differentiating between the cytoplasmic and nuclear forms of these components. Furthermore, we include the phosphorylated states of proteins since studies suggest that these phosphorylated states may affect protein localization and degradation. The models presented by Leise and Moin (2007), Ruoff et al. (2005), and Xie and Kulasiri (2007), for instance, ignore the role of phosphorylation, while Xie and Kulasiri also exclude compartmentalization. Additionally, we associate protein degradation rates with the number of bound phosphates as evidence suggests that hyperphosphorylated proteins may degrade more quickly (Akten et al., 2003; Cyran et al., 2005; Hardin, 2005; Kim et al., 2007; Ko et al., 2002; Lin et al., 2002; Schoning and Staiger, 2005).

Unlike modeling studies that fit parameters to both wild-type and mutant data (Locke et al., 2005), we predict mutant phenotype behavior de novo. Simulations of the 29-state model show excellent agreement with experimentally observed expression profiles in free-running, entrained, and mutant phenotypes. Even further, our model proves to be robust to both variations in day length and initial conditions; system dynamics converge to the same limit cycle with respect to initial conditions as small as 0.5 nM and as large as 100 nM.

Model Comparison

Since experimental data (specifically amplitude measurements) are noisy and varied, we find it necessary to identify accurate performance attributes that best describe the system. In the case of circadian oscillators, this performance criterion is phase. Many models, however, fail to acknowledge light entrainment and phase entrainment. To better assess the utility of the 29-state model, we compare its network and dynamics with those of recently published circadian systems. In Table 1, we outline the attributes captured by the 29-state model and compare the results with those exhibited by other recent models. In particular, we investigate the kinetics responsible for the proper phase-response behavior exhibited in several other circadian models (Leise and Moin, 2007; Leloup and Goldbeter, 1998; Smolen et al., 2004; Ueda et al., 2001; Xie and Kulasiri, 2007).¹⁰ Despite the fact that CLK is exclusively responsible for the activation of per, tim, vri, and pdp, many models incorporate TIM as a secondary regulator of gene expression by incorporating nuclear TIM protein concentrations in the transcription (Leise and Moin, 2007; Leloup and Goldbeter, 1998; Smolen et al., 2004; Ueda et al., 2001). The only other model that claims to produce accurate PRC dynamics without the explicit modeling of light-induced protein concentrations in gene expression kinetics is the one presented by Xie and Kulasiri (2007). We were unable to verify their claims due to inconsistencies in the article. The model presented by Kuczenski et al. (2007) does not address circadian phase dynamics or light-induced phase response. The model presented by Leise and Moin (2007) does not include appropriate light-entrained dynamics; our simulations of their model subject to regular 12-h light/dark cycles show 48-h harmonic effects. The model we found that most accurately depicts phase dynamics is presented by Smolen et al. (2004) and incorporates all 5 clock components. The Smolen et al. model includes phosphorylation and compartmentalization, exhibits mutant phenotype behavior, and generates an accurate PRC. The kinetics, however, do not characterize mRNA dynamics and involve the use of an explicit time delay that enforces the required 3- to 6-h time lag between nuclear VRI and PDP peak concentration levels. This timing mechanism is necessary for the accurate regulation of clk mRNA. clk dynamics are also known to oscillate antiphase to per, tim, vri, and pdp, the model presented by Smolen et al. provides a 5-h time difference while our model reflects an 11-h difference (Table 1). A related point of interest relevant to circadian model comparison involves phase-based sensitivity analysis (Bagheri et al., 2007) with respect to changes in photoperiod. Such an investigation may point to how organisms adapt to variations in day length by modifying their respective phase alignments at the molecular level.