Figure 8.

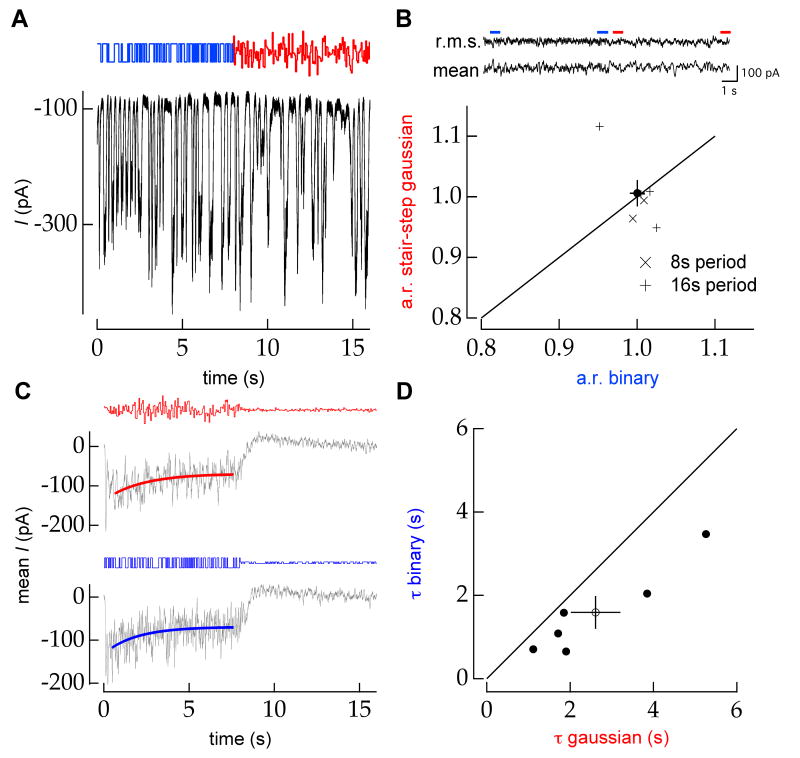
Higher-order moments of the stimulus distribution affect the time course of adaptation to changes in stimulus contrast. A, Example record (black trace) of the excitatory synaptic input current to an ON RGC in response to a periodic (T=16s) switch in stimulus distribution from binary to Gaussian (mean and variance held constant) (top). B, The mean and r.m.s. synaptic input current during ∼50 periods like that shown (C) (top). Although there may be a change in the structure of the response distribution, there is no obvious adaptation. Adaptation ratio (a.r.) for each condition was defined as the ratio of mean synaptic current in the second and last 500ms of each condition (indicated by red and blue bars). Combining results of measurements from T=8s and T=16s periods, the adaptation ratio for stair-step Gaussian and binary conditions are not significantly different from 1 (bottom; 1.01 ± 0.02 vs. 1.00 ± 0.01 (mean±sem); p=0.91 and p=0.99, respectively). The black circle shows the population mean. Error bars show standard error of the mean. C, The time constant of an exponential fit (red) to the mean excitatory input to an ON RGC to a periodic 6-36% contrast step in a stair-step Gaussian distribution (top) is longer than the time constant of the exponential fit (blue) to the mean response to a periodic 6-36% contrast step in a binary distribution (bottom). Stimuli were updated at either 11 or 19Hz and results were averaged across all trials. Example stimuli for the Gaussian (red) and binary (blue) conditions are shown above each trace on equal vertical scales. D, Across a population of ON RGCs (n=6), the timescale of adaptation is longer for periodic contrast steps in a stair-step Gaussian distribution than for similar contrast steps in a binary distribution (2.6 ± 0.6 vs. 1.6 ± 0.4 s mean±sem; p = 0.015, paired t-test). The solid line marks equality. Each filled circle represents one cell and the open circle marks the population mean.