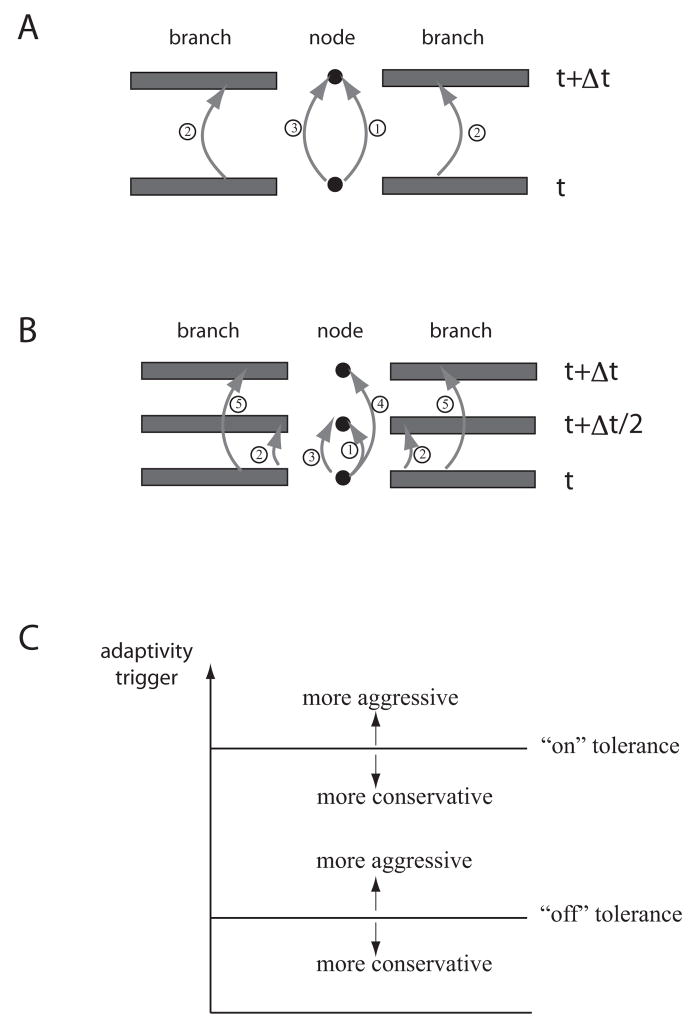
Figure 1.

Overview of the numerical method. Each version of the method is illustrated on a simple configuration of two branches connected by a node. Both update schemes are designed to mimic an ordinary update using either backward Euler or Crank-Nicolson for the branches and nodes. A, Schematic of the backward Euler version of the predictor-corrector numerical method, indicating the three steps of the method: an explicit update for the nodes, an implicit update for the branches, and a corrector step for the nodes. Note that here “node” refers to any location where two or more branches connect. B, Schematic of the Crank-Nicolson version of the predictor-corrector numerical method. The first three steps are identical to the backward Euler predictor-corrector update except they are taken for only half of a time step. The additional two steps (steps 4 and 5) are explicit updates for the nodes and branches, consistent with performing Crank-Nicolson as a two-step update. This approach is meant to mimic the standard Crank-Nicolson update in a branch. See our previous work for details of the algorithm (Rempe and Chopp, 2006). Both update schemes were designed to de-couple the branches from one another. C A plot of the adaptivity trigger and sample values for the “on” and “off” tolerances. If the “on” tolerance is made larger, branches don’t turn on as quickly, making the adaptivity more aggressive. Smaller values of the “on” tolerance mean branches begin computing when a small trigger value is measured. This is referred to as conservative. For the “off” tolerance, making this value larger means branches will more easily be turned off, this is called more aggressive. If the “off” tolerance is made smaller a branch is not turned off until the trigger value is extremely small, this is considered more conservative. Modified from Rempe and Chopp, 2006.