Fig. 1.

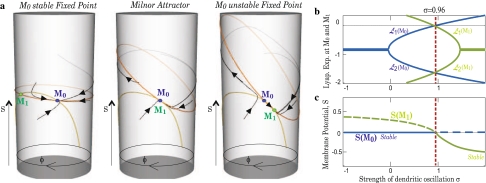
Fixed points analyses for one cell. a Cylinder space (S,ϕ) with nullclines (orange for dS/dt = 0, yellow for dϕ/dt) and some trajectories. Left to right shows the three possible scenario: M₀ is stable fixed-point for μ < μ_c, M₀ is the Milnor attractor for μ = μ_c and M₀ is unstable fixed-point for μ > μ_c. b Evolution of the two Lyapunov exponents of the system at M₀ (in blue) and M₁ (in green) in function of σ (ρ = 1). As expected, one exponent becomes null at σ = μ_c. c Evolution of the two fixed points, M₀ and M₁, when σ is varied. μ = μ_c corresponds to a transcritic bifurcation