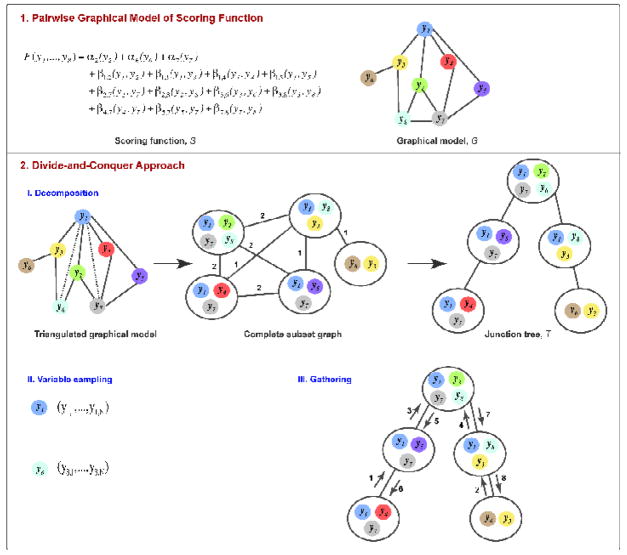
Figure 1. DOMINO outline.

(1) The DOMINO optimizer is illustrated with the scoring function F of 8 variables {y_i} composed of a sum between 3 single body terms {α_i} and 11 pairwise terms {β_{i, j}}. The scoring function is encoded in the graphical model G. (2) (I) Decomposition of the graphical model results into a junction tree T ²³; ²⁴. The graphical model is first triangulated; a graph is triangulated if there are no cycles with more than three edges without a chord (a chord is an edge connecting two non-adjacent nodes in a cycle). The triangulation procedure adds edges (dotted lines) to the graphical model until no cycle is chordless. The triangulated graphical model is then converted into a complete subset graph. The nodes of the complete subset graph are maximum cliques in the triangulated graphical model (gray circles); a maximum clique is a sub-graph whose nodes are connected directly to each other and are not all part of another clique. The weight of an edge in the complete subset graph is the number of the shared variables between the adjacent subsets, as indicated; edges of weight zero are not shown. Next, the junction tree is the maximum spanning tree of the complete subset graph; a maximal spanning tree of a graph spans all of the nodes without cycles, using a subset of the original edges with the maximal sum of their weights. (II) The sampling space of each variable is discretized. (III) Finally, the globally optimal solution of F is gathered from enumerated subset states by passing messages between subset nodes. The numbers on the edges indicate a valid sequence of message passing.