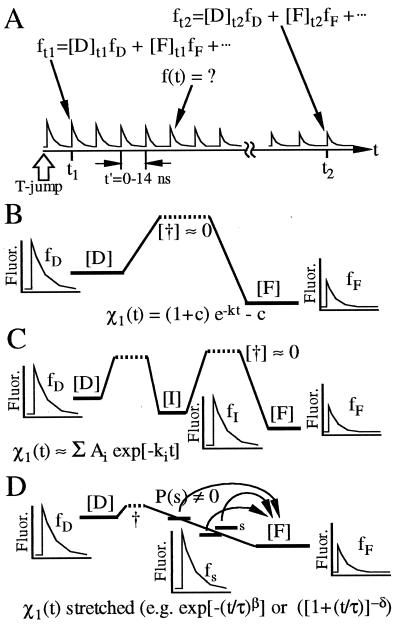
Figure 4.
(A) After a T-jump, time-resolved fluorescence transients change shape from ft1 to ft2 because of folding between t1 and t2. If only D and F are significantly populated during folding, ft1, ft2 and ft are linear combinations of the denatured fluorescence signal fD and native fluorescence signal fF; otherwise, other populations contribute to ft1 and ft2. (B) Two-state model. [D]t1 and [F]t1 relax exponentially in time to [D]t2 and [F]t2 without significantly populating “†”. f(t) is a weighted average of fF and fD and hence of ft1 and ft2. χ1(t) therefore decreases exponentially, no matter at which time ft1 and ft2 are picked. The same holds true for a three-state reaction with two time scales τ1 and τ2, if τ2 ≫ τ1 and f2 is picked at t ≪ τ2. (C) Sequential intermediates. fI is not necessarily well represented by a linear combination of ft1 and ft2. If it is, χ1 is a linear combination of exponentials with uncorrelated lifetimes and amplitudes, some of which may be negative (e.g., if fI ≈ fD ≠ fF). If it is not, χ2 for the fit to Eq. 1 is greater at intermediate times than at t1 and t2. (D) Downhill scenario. A heterogeneous downhill folding ensemble is populated during folding because of the small transition state barrier †. If the subensembles {s} with different fluorescence fs interconvert slowly, the rate laws of individual s add separately (Eq. 2), yielding a smooth nonexponential χ1(t). The nonexponentiality can be homogeneous or inhomogeneous depending on the interconversion rates among and within subensembles (11, 12, 19).