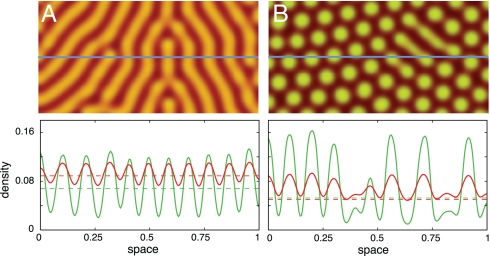
Fig. 2.

Typical stationary patterns for diffusion-induced instability (Turing patterns) (A) and diffusion induced coexistence (B) on an L × L square (no flux boundaries). The density variation of cooperators (green) and defectors (red) is shown along a cross-section (solid blue line). (A) In the absence of space, cooperators and defectors coexist for suitable initial configurations (r = 2.4 > r_Hopf = 2.3658). Diffusion destabilizes the spatially homogeneous state and induces stable and static heterogeneous strategy distributions, where individuals spontaneously aggregate in spots or striped patterns. (B) In the absence of space, the population goes extinct (r = 2.24 < r_Hopf). Diffusion stabilizes persistence of the population and coexistence of cooperators and defectors by inducing heterogeneous strategy distributions. In both scenarios, the parameters of the ecological public goods are n = 8, c = 1, d = 1.2, b = 1, D_C = 1, D_D = 10, with an initial configuration where densities are randomly drawn in [0, 0.1]. Numerical integration is performed on a spatial grid with L = 283, dx = 1.4, and a step size of dt = 0.1. The brightness of the colors indicates the strategy densities (Upper) and the dashed horizontal lines mark the densities at Q (Lower).