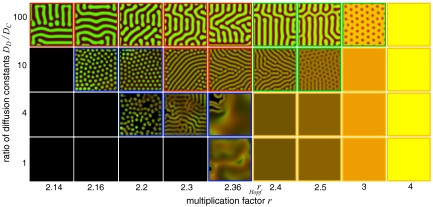
Fig. 3.

Diversity of spatial distributions in terms of the ratio of the diffusion of defectors to cooperators D_D/D_C and the multiplication factor r in spatial ecological public-goods games. The brightness of the colors indicates the density of cooperators (green) and defectors (red). In the absence of space, the population survives for r > r_Hopf. If cooperator diffusion exceeds defector diffusion, D_D/D_C ≤ 1, the dynamics is barely affected by space, except for a small chaotic region (blue frame) near r_Hopf. The dynamics becomes much richer for D_D/D_C > 1. For r < r_Hopf, the chaotic regime increases (blue frame) and is replaced by diffusion induced coexistence patterns for high D_D/D_C (red frame). For r > r_Hopf, the homogeneous spatial distributions (orange frame) are replaced by diffusion-induced instability (Turing patterns; green frame) for high D_D/D_C. For very large r, all patterns disappear. The parameters are N = 8, c = 1, d = 1.2, b = 1, D_C = 1, L = 283, dx = 1.4, dt = 0.1 (r_Hopf = 2.3658) and an initial configuration with random cooperator and defector densities in [0, 0.1]. For a detailed phase plane diagram and other initial configurations see SI Text and Figs. S1 and S5.