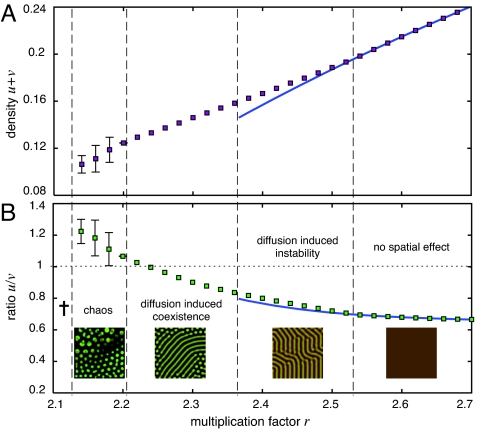
Fig. 4.

Average global population density (A) and ratio of cooperators to defectors (B) as a function of the multiplication factor r in ecological public-goods interactions. The nonspatial stable equilibrium (solid lines; requires r > r_Hopf) is shown together with numerical results for the stationary spatial distributions (dots). The chaotic regime depicts the average and standard deviation of the time series from t = 5,000 to 10,000 with dt = 0.1, dx = 1.4 and L = 283. For small r, the population goes extinct, but for increasing r, the population persists and exhibits chaotic dynamics that change into quasistatic and static patterns emerging through diffusion-induced coexistence (r < r_Hopf). For r > r_Hopf, static patterns are triggered by diffusion-induced instability (Turing patterns) and relax into spatially homogeneous coexistence for high r. Diffusion supports cooperation by significantly increasing the persistence region of the population and in the chaotic regime, cooperator densities even exceed those of defectors. Snapshots illustrate typical patterns emerging in the different dynamical regimes. The brightness of the colors indicates the density of cooperators (green) and defectors (red). The parameters for the ecological public goods game are N = 8, c = 1, d = 1.2, b = 1, D_C = 1, D_D = 10 such that r_Hopf = 2.3658.