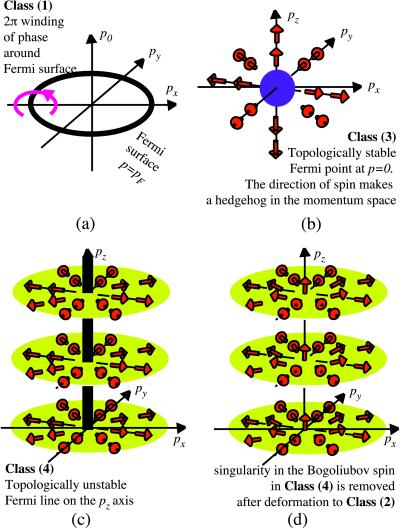
Figure 2.

(a) Winding of the propagator phase around the FS. For simplicity the p_z coordinate is hidden so that the FS is the line (p₀ = 0,p = p_F) in the 2+1 momentum space. This line is a singularity, which is similar to a vortex in a real three-dimensional space. The phase of the propagator G = (ip₀ − (p_x² + p_y² − p_F²)/2m)⁻¹ changes by 2π around the line in the momentum space in the same manner as the phase of the order parameter changes by 2π around a vortex in the real space. (b) Fermi point at p = 0 in the three-dimensional momentum space (p_x,p_y,p_z). At this point the particle energy E = cp is zero. A right-handed particle is considered with its spin parallel to the momentum p, i.e., s(p) = (1/2)p/p. The spin makes a hedgehog in the momentum space, which is topologically stable. (c) Fermi line, topologically unstable manifold of zeroes, is shown in the three-dimensional momentum space (p_x,p_y,p_z). The (Bogoliubov) spin (arrows) is confined into the (p_x,p_y) plane and has a singularity on the p_z axis. (d) This singularity can be removed by a continuous transformation. The spin escapes into a third dimension (p_z) and becomes well defined on the p_z axis. As a result, the quasiparticle spectrum becomes fully gapped (the relativistic fermion acquires the mass).