Inside the Sausage Factory: Improving Estimates of the Effects of Health Insurance Expansion Proposals

Many policy proposals address the lack of insurance coverage, with the most commonly discussed being tax credits to individuals, expansions of existing public programs, subsidies for employers to offer coverage to their workers, and mandates for employers and individuals. Although some policy options may be favored (or disfavored) on theoretical or ideological grounds, many debates about policy center on empirical questions: How much will this option cost? How many people will obtain insurance coverage?

Estimates of costs and consequences influence policy in three ways. First, the Office of Management and Budget, the Congressional Budget Office, the Centers for Medicare and Medicaid Services, the Treasury Department, and other government agencies incorporate estimates of the costs of proposals in their budget calculations. Particularly in times of fiscal restraint, the cost of a proposal is central to its legislative prospects. Second, recognizing the importance of final budget numbers, policy advocates include estimates in their advocacy. For example, over the past three years in projects sponsored by the Commonwealth Fund, the Kaiser Family Foundation, and the Robert Wood Johnson Foundation (RWJF), analysts have made proposals addressing the problem of uninsurance, including estimates of the costs and the consequences of these proposals. Finally, estimates of policy proposals offer a shorthand way of summarizing a great deal of information about how people will respond to them.

The resulting demand for estimates of costs and consequences has generated a corresponding supply of estimators. Estimators, usually economists, may work for federal agencies, and those who do not, work mainly as independent consultants in think tanks (e.g., the Urban Institute), consulting firms (e.g., the Lewin Group), or academic institutions. For example, the estimates commissioned by Commonwealth, Kaiser, and RWJF were conducted by Jonathan Gruber of MIT and Sherry Glied of Columbia University, the Urban Institute, and the Lewin Group, respectively. Recently, lobby groups, such as the American Medical Association, have hired in-house estimators.

The policy proposals often differ in their specifics, making it hard to provide side-by-side comparisons of cost differences. In table 1, however, we show two sets of examples of very similar proposals (for tax credit expansions and the Children's Health Insurance Program [CHIP] as implemented) produced by various estimators. As the table shows, the estimators differ, often by quite a bit. Tax credit costs per newly insured person vary by a factor of 3. In the CHIP proposal, the budget appropriation was already fixed, but there was a 30 percent difference between the estimators in forecasts of the number of children who would be covered under the program. These variations resulted from the different models that the estimators used.

TABLE 1.

Divergence among Predictions of Health Insurance Expansions

	Refundable Tax Credit for Nongroup Insurance ($2,000 Individual/$4,000 Family)a			Children's Healthcare Insurance Program (CHIP) Expansions as Implementedb
	Gruber and Levitt 2000	AMA 2000	RWJF 2000	Holahan, Uccello, and Feder 1999	Selden, Banthin, and Cohen 1999
Total Take-up (total number participating)				1.8 million	1.5 million
Net Number of Newly Insured People	7.7 million	18 million to 20 million	8.6 million	1.2 million	0.9 million
Cost per Newly Insured Person	$4,915	$1,807 to $2,442	$7,400

Notes:

^aEligibility for tax credit is based on income and varies across models. Income cutoffs are $60,000 for single persons and $100,000 for families for Gruber and Levitt; up to $75,000 for the AMA; and <$150,000 for Lewin.

^bIncorporates state-specific CHIP eligibility criteria.

All estimators begin by developing simulation models of the health care system. They base these models on economic theory and the available empirical literature, which is limited and often highly disputed. Different modelers interpret the theory and evidence differently, thus producing varying estimates of costs and consequences. The underlying uncertainty in the literature implies that the costs and consequences of specific proposals also should be uncertain. Ideally, the variation in the predicted impacts among models of a proposal should itself yield information about the degree of uncertainty surrounding the proposal. Policy analysts should be able to choose among estimates according to their own assessment of this evidence. In addition, an understanding of the features that generate uncertainty should guide future research and survey design.

As typically presented, however, estimates do not fulfill any of these functions, and policy analysts cannot choose among them by comparing their assumptions. There is no reason to believe that the range of estimates describes the extent of uncertainty around them. Indeed, it is almost impossible to understand why estimates based on different models differ. These failures of transparency are a consequence of the institutional context in which estimators operate.

Simulation models are based on findings in the empirical economics literature, but they are not themselves academic products. While estimates are sometimes published in journals, simulation models are not generally subjected to formal peer review. At first, many estimators kept the workings of their models completely secret. Now, increasingly, estimators do report information about how their models work, but each team uses its own reporting schema. Information obtained from one modeler is usually in a form that cannot be compared with information from another modeler.

This lack of comparability models undermines the modeling enterprise. The resulting variability suggests that the models yield no genuine information. Worse, it raises the suspicion that estimates are made to accommodate the preferences of the estimator's patrons. It would, however, be a mistake to abandon simulation modeling altogether.

Quantitative models give policymakers a sense of a program's size and scope that can never be obtained from theory and qualitative analysis alone. A model's results inform choices among policy options and guide the elaboration of program details. Estimates eventually enter the legislative process as budget forecasts, and the need for budgeting means that we must have simulation models. Accordingly, we must improve the modeling enterprise in both government and the private sector. The latter is particularly important because without credible evidence from the private sector, government estimates cannot be effectively challenged.

Models should inform policymakers in a readily digestible way about what researchers know. Models should reflect the nature and extent of disagreements among researchers and serve as a guide for future research. They should reveal to policymakers that uncertainty about consequences exists and that they should be cautious about accepting model-based predictions. Both individually and collectively, modelers possess the skill and the art of translating policy ideas into tangible costs and quantities. Because they work outside an established research paradigm, the substance of modeling could be improved by establishing such a paradigm.

In this article we describe the key elements of developing simulation models, a process that is somewhat akin to sausage making. Of course, the insides of a sausage factory are not a pretty sight. For a general health policy audience that has been eating sausage for a long time, however, a better understanding of the ingredients may be valuable.

In addition, we propose that modelers adopt a set of conventions, which we call a reference case, to report the results of simulation modeling. Our use of the term reference case reflects a similar effort to develop a prototype for cost-effectiveness analyses (Gold et al. 1996). As in that instance, the reference case is a guide to modelers describing their models and helps them better convey their information to the policymaking community. By adopting a uniform set of reference conventions, modelers make it easier for policymakers to compare the models and the programs estimated by these models. At the same time, reference conventions should make more transparent the uncertainty within the models and the disagreement among them. The specific reference case we developed appears as an appendix to this article.

Modeling Frameworks

Models of health insurance expansions have two ingredients: a basic structure and a set of parameters. The basic structure provides a framework describing the numerous decisions associated with obtaining insurance coverage. Modeling parameters describe the magnitude of the elements that affect the decision to buy insurance and are discussed in greater detail in the next section.

Modeling this decision is complicated because in our fragmented health insurance system, the decision itself is complicated. Every person faces an elaborate array of coverage choices. Consider the decision facing someone with employer-sponsored coverage when a new public program is introduced. The new program might lead the person's employer to reduce (or increase) its share of the cost of coverage or to drop the coverage altogether. If the employer changes its behavior, the person may keep her coverage, drop her coverage, switch to individual coverage, or join a public program, all depending on her eligibility and other characteristics. Even if the employer makes no changes, she may decide to drop her coverage anyway and join the new program. All this assumes no spouse, no children, and no insurer behavior.

All simulation models take shortcuts when establishing a structure to describe this framework. Some of the differences between models are differences in these shortcuts. No simulation model could ever hope to reproduce the level of detail in the real world, for most of the parameters are simply not known and cannot be known.

In practice, one of four basic structures is used to model insurance participation. The first, which we call the elasticity approach (EA), applies measures of the responsiveness of insurance purchase decisions to changes in price (price elasticities) to data describing current prices and current insurance patterns. This approach is the most familiar and widely used (Baumgardner 1998; Gruber 2000).

We call the second approach the discrete choice approach (DCA). This method estimates a regression model of the probability that an individual has insurance as a function of price and many other variables (Custer and Wildsmith 1999; Pauly and Herring 2002; RWJF 2000). Then the fitted regression model is used to predict the number of insured persons given the new program's prices and other features.

The third approach, which we call the matrix approach (MA), breaks the population into groups defined by particular characteristics, such as income and family size. It applies a range of group-specific take-up rates to determine what share of each of the different groups will participate (the take-up rate is the share of the population who are initially uninsured who “take up” insurance in response to a price or policy change). The matrix approach has been used primarily for Medicaid take-up calculations. Some estimates using the matrix approach also include price as a grouping category (e.g., see Holahan, Uccello, and Feder 1999).

We call the fourth approach the reservation price approach (RPA). A reservation price is the highest price at which a given individual would purchase health insurance. The RPA compares new health insurance options with estimated reservation prices (Pauly and Herring 2001, 2002). Since reservation prices cannot be directly observed, modelers who adopt this approach must simulate them using more or less complex modeling methods (e.g., see Pauly and Herring 2002; Zabinski et al. 1999).

While closely related, these four approaches are not identical (Remler, Graff Zivin, and Glied 2002). Each approach makes different assumptions about the unobservable characteristics of people in the model, characteristics that are not included in the available data. For example, the models implicitly assume different things about how responsiveness to health insurance price varies with the desire for more or less aggressive medical care. These varying assumptions can lead to differences in the estimates, especially when they predict behavior far removed from current conditions. Since the differences among the models are a consequence of how they treat unobservable characteristics, they are, by definition, unavoidable.

The most immediately relevant problem with the coexistence of these approaches is that each approach uses a different language to describe how it works. Consider the question of whether someone chooses to participate in an insurance program. The EA describes this behavior in terms of price responsiveness, measured as an elasticity. The DCA also looks at price responsiveness, among other features, but measures price responsiveness as a regression coefficient. The MA describes this same behavior in terms of take-up behavior. The RPA describes the behavior in terms of a reservation price. Without further translation, it is not possible to know whether the assumptions used in different models are essentially the same or quite different.

It is possible—though difficult—to translate parameters between approaches. And if the models using each approach also use identical parameter estimates, the choice of approach will not be empirically very important to the types of incremental reforms that policymakers are now considering. However, within and across approaches, different modelers often use quite different values for the same implicit parameter. Consequently, differences in parameter values are the main source of differences among estimates.

Modeling Parameters

Modeling health insurance expansions based on the structures just described involves selecting values for the levels and responsiveness of each of the key variables. Each model has many parameters, so choosing values for them is very difficult. Furthermore, estimators often lack good data that would enable them to capture the program's features. Surveys vary considerably in the simple counts of the number of uninsured people, in estimates of prevailing health insurance premiums, and in the number of presumed eligible persons for each program.

We have little historical or experimental evidence concerning the important parameters that affect coverage expansion estimates. The Medicaid expansions of the late 1980s provide much of the evidence that we do have, but they affected only subgroups of the population (children and pregnant women) and focused on a very low income group. Alone, the expansions do not even provide enough information for precise estimates of the effects of Children's Health Insurance Program (CHIP) expansions to slightly higher income children. Although the self-employed have benefited from the expanded tax deductibility of premiums, this group constitutes only a small portion of the population, and their circumstances differ substantially from those of the rest of the population. The Health Insurance Tax Credit experiment of the early 1990s was also quite limited in both scope and size.

The results of the nonexperimental research that is available to inform simulation models vary substantially and often are only indirectly related to the problem at hand. Most analyses were conducted to test specific hypotheses about behavior in specific instances, for example, the extent of the crowd-out1 of private insurance by public insurance (Cutler and Gruber 1996; Dubay and Kenney 1996) or the response of self-employed people to a change in tax rates (Gruber and Poterba 1994). These analyses can sometimes provide very precise information about responsiveness to specific policy changes. But the results themselves are often not in a form that makes them useful to simulation modeling.

This is not to say that modelers never agree. In a few areas, modelers do agree about parameter values. For example, nearly all modelers use estimates from the RAND health insurance experiment to calculate medical care utilization responses to changes in copayment and deductible rates (Newhouse 1993).

Table 2 lists many of the important parameters needed to estimate the effects of particular expansion proposals, and it also notes some of the controversial issues. Rather than discuss each of these parameters in detail, we examined a sample of them to demonstrate the types of issues that arise in selecting them. We chose these issues both because they are of intrinsic importance and because they illustrate the kinds of the problems associated with modeling. Further details are available in the reference case document in the appendix.

TABLE 2.

Key Parameters and Issues for Modeling Health Insurance Expansions

Parameter	Key Issues	Selected Citations
Baseline
Number of Uninsured Persons	Disagreement among data sources; modeling the characteristics of the uninsured	Dubay and Kenney 2000; Lewis, Ellwood, and Czajka 1998
Premiums Paid by Consumers	Imputation of prices; prices of policies declined; price variation with health status	Blumberg and Nichols 2000; Curtis et al. 1999; Selden and Moeller 2000; Swartz and Garnick 1999; Zabinski et al. 1999
Eligibility for Existing Public Health Insurance Programs	Lack of data for many eligibility criteria (e.g., assets); eligibility changes due to behavioral responses	Blumberg and Nichols 2000; Daponte, Sanders, and Taylor 1998
Price Responsivenessa
Elasticity/Take-up	Reporting methods across different approaches; −0.4 to −0.6 elasticity	Feder, Uccello, and O'Brien 1999; Gruber 2000; Gruber and Poterba 1994; Holahan, Uccello, and Feder 1999; Royalty 2000
Heterogeneity: Does Price Responsiveness Vary with Other Characteristics?	Variation by income: does responsiveness rise or fall? Variation by health status	Marquis and Long 1995; Monheit and Schur 1988; Pauly and Herring 2002; RWJF 2000
Crowd-out: Do People with Existing Employer-Sponsored Coverage Also Respond to New Programs?	Substitutability of different programs	Cutler and Gruber 1996; Dubay and Kenney 1996; Thorpe and Florence 1998
Nonprice Factors That Encourage or Deter Participation
Stigma	Lack of quantitative data	Remler and Glied, 2003
Family Decisions	Spousal decisions; desire for “family unification”	Bilheimer and Reischauer 1995
Employer's Behavior
Employer's Decision to Offer Health Insurance	Variation by firm size: offer elasticities, −0.6 to −1.8 for small firms and 0 to −0.2 for large firms	Blumberg and Nichols 2000; Feldman et al. 1989; Gruber and Lettau 2000; Marquis and Long 1995; Stabile 2002
Employer's Contribution (share of premium paid by employer)	Estimating price responsiveness; variation by firm size	Dranove, Spier, and Baker 2000
Incidence (degree to which wages fall owing to employer's health insurance costs)	Completeness; time scale	Gruber 1994; Sheiner 1999

Note:

^aPrice and nonprice responsiveness include parameters that help predict how many people eligible for an insurance program or a particular set of benefits will actually avail themselves of it.

The parameters summarized in table 2 fall into four categories. The first category describes the world before a proposal is implemented. It includes the number of uninsured people, the existing level of health insurance premiums, and the eligibility criteria of public programs already in operation. The existing data sources do not, however, provide a complete picture of any of these parameters. The second category of parameters describes how people respond to the price of health insurance. Most models include an overall price responsiveness parameter, and in some models this parameter is varied to reflect the heterogeneity of other characteristics. For example, in some models, lower-income people are expected to be more responsive to a change in price than are higher-income people. Price responsiveness may also vary according to whether or not people are initially privately insured, thereby affecting the extent of crowd-out associated with a new program. The third category of parameters includes the nonprice determinants of response, such as stigma, or the benefits of having an entire family covered by the same insurance plan. The final category of parameters describes employers’ decisions to maintain, add, or drop coverage, to adjust the employees’ contribution level, and to compensate for changes in health insurance coverage through adjustments in wages.

How to Make Estimates

Much of the debate among modelers concerns the proper methodology for estimating parameters. The most important set of estimates used in any simulation model of a health insurance expansion consists of parameters that describe the responsiveness of individuals and employers to a change in price. For simulation purposes, an ideal set of estimates of a responsiveness parameter, such as the price elasticity of demand for health insurance, would have four properties. First, it would be based on price data that corresponded to the actual prices faced by each individual, not imputed data based on yet further assumptions. This is almost always impossible to accomplish because we know, at best, only the prices paid by those who actually purchase coverage. We rarely know the prices for coverage offered to those who do not buy coverage, and they are the ones whose behavior interests us most. Imputations raise the danger that the estimated responsiveness depends on the method used to impute the data.

Second, the ideal parameter would be measured using variations in prices that were truly exogenous to the individuals in the study, that is, price variation that was not a result of individual behavior but of some forces beyond a person's control. For example, because health insurance prices are higher for people with more serious health problems, they often buy whatever coverage is available to them, despite the high price. If price variation in the data reflects differences in (unobservable) health status, it will appear as if people are not very responsive to prices. Other forms of unobservable variation similarly confound responsiveness measures. In general, without exogenous variation, estimated responsiveness may be biased.

Third, the ideal parameter would be estimated from a population similar to that under consideration. If the parameter is based on the behavior of another population, it may not reflect how the population under study would behave. For example, estimates of responsiveness based on the behavior of self-employed people who faced a change in the tax treatment of their health insurance in 1986 may provide very little information about the behavior of poor families offered an opportunity to buy coverage through the Children's Health Insurance Program (CHIP) at low rates.

Fourth, an ideal set of estimates would fully capture any heterogeneity in price responsiveness in the population under study. A model describing the behavior of an average person may not accurately capture how the entire distribution responds to a price change.

In practice, no data contain complete prices, describe exogenous price changes, focus on the population eligible for any conceivable coverage expansion, and have enough information to incorporate heterogeneity. Collecting better data of this type has been a research priority since (at least) the Clinton administration's reform effort (Bilheimer and Reischauer 1995; Nichols 1995). Some efforts to gather such data are under way (the Agency for Healthcare Research and Quality now conducts a continuous panel survey of expenditures and premiums, and the Center for Studying Health System Change's Community Tracking Survey collects information from employers and consumers). This type of information is very difficult and costly to collect, and even the best surveys cannot generate exogenous price variation because some of the price variation in these surveys is a result of individual decisions such as choices about where to work.

Some analysts argue that the most important feature of any estimate is that it is based on exogenous price variation. The expansion of the favorable tax treatment of health insurance to the self-employed is one example of such exogenous variation. Other analysts assert that fidelity to the population eligible for the new expansion is the most important feature, and they prefer to estimate parameters using the current behavior of the sample under study.

In the absence of ideal data, modelers need to balance considerations of exogeneity with those of data fit. Both sides make intellectually respectable arguments. But while this question has generated a heated debate among economists, what is striking when examining the literature is the substantial variation among estimates produced using each of these approaches (for relevant summaries, see Gruber 1994; Pauly and Herring 2002). Until we have a better way of sorting out the merits of exogeneity versus data representativeness, modelers should allow policy analysts to assess the validity of their assumptions by making explicit the degree of exogeneity and representativeness associated with their estimates.

Comparing Estimates across Models: Responsiveness of Demand to Changes in Price

One problem with the way that current estimates of health insurance expansions are presented is that they lack comparability. One place where this is evident is in the measurement of price responsiveness. Most health insurance expansion proposals envision changing prices, in many cases changing financial prices to zero, so that in most studies the responsiveness of the demand for health insurance to its price is the central parameter. There is considerable variation in estimates of this parameter in the empirical economics literature, but most studies find that the purchase of insurance is somewhat, but not very, responsive to price.

Studies that use the EA method implement this parameter using a price elasticity of demand, which measures the percentage change in the number of insured that would accompany a 1 percent decline in the price of coverage. The literature yields a wide range of estimates for this parameter (Gruber 2000). Results from three recent studies report a narrower but somewhat higher range of estimates than did much of the earlier work, with the results falling into a band between −0.4 and −0.6 (Gruber and Poterba 1994; Marquis and Long 1995; Royalty 2000). These estimates imply that a 1 percent decline in the price of insurance would raise the number of insured people by 0.4 to 0.6 percent.

Some estimators who use the DCA compute responsiveness from the same data that they later use for predictions. Specifically, they conduct regression analyses of the data, modify the prices for individuals according to the policy proposal under study, and simulate the outcomes in the model (Custer and Wildsmith 1999; Pauly and Herring 2002; RWJF 2000). These modelers do not always report a price elasticity that corresponds to the results of their regression analysis, but they could readily do so. The one model that does so reports a price elasticity parameter based on its data of −0.2, somewhat lower than the range in recent published studies (RWJF 2000).

The RPA compares new prices with reservation prices, or the maximum price that a person is willing to pay for coverage. The reservation prices are estimated in various ways. Pauly and Herring (2002) used an actuarial method called induction to predict what the health expenditures of the uninsured would be if they were insured. Predicted expenditures for the future are calculated as a weighted average of actual expenses and cell (age, gender, health status) averages. For each uninsured individual, the reservation price is computed as the sum of four components: the magnitude of out-of-pocket expenses, the cost of risk due to the lack of coverage, the value of added utilization induced by new coverage, and the quantity of free care that a person may receive. Details of how the calculations are made, particularly the assumptions about attitudes toward free care, result in very different reservation prices for the currently uninsured. For example, the mean reservation prices for a standardized insurance package range from $128 to $1,348 depending on the assumptions made. The size of reservation prices affects the response to a price change, since people are expected to switch coverage if the new price is below the old price. But unlike the price elasticity measure, it is very difficult to know what degree of responsiveness is implied by a particular set of reservation prices. Although price elasticities are not an automatic output of reservation price models, they can be easily constructed while the simulations are conducted.

The MA uses a take-up probability rather than an elasticity to compute the take-up rate within a group. Since the MA has been used mostly for public program expansions, the take-up probabilities are probabilities associated with Medicaid. Take-up rates are computed based on the observed take-up as a function of family income and premiums (for those programs that impose premiums on higher-income participants) as a share of income (Feder, Uccello, and O'Brien 1999; Holahan, Uccello, and Feder 1999). Take-up rates for a new program are computed for each income group by subtracting the number of participants at the current premium from the estimated total number of participants at the new program premium and estimating the take-up rate among the uninsured that would be needed to achieve this total. Take-up rates for programs with nonzero prices are adjusted to reflect (implied) price response. A take-up rate is similar to an elasticity, but it needs to be manipulated further to be directly comparable. Modelers using the MA have all the information in their models that is needed to report the price elasticities implied by the take-up rates they use.

Although there is no reason (at least at present) to prefer the EA to any of the other modeling structures, the existing empirical literature in economics measures price responsiveness in terms of elasticities. This makes an elasticity measure the most natural way to compare assumptions about price responsiveness across models. Comparing estimates would be easier if policy analysts required modelers to reveal the price elasticities implied by the model they use, regardless of that model's structure. This information could guide decisions about the reasonableness of responsiveness assumptions.

This discussion suggests that it would be relatively straightforward—and useful—for modelers to use a standard reporting convention for price responsiveness. But this convention by itself is of limited value. The price elasticity of the demand for health insurance (or its equivalent in other models) is a single parameter. The single value chosen for this parameter affects the costs and consequences of every proposal for insurance expansion, but models that use different values for this parameter would still rank proposals in the same order. The price elasticity of demand may, however, vary with income. If it does, then models that use different income-price combinations may yield both different cost levels and different proposal rankings for proposals that affect different income groups.

Little evidence is available regarding whether the price responsiveness of the demand for health insurance varies with income. Economists generally think that price elasticities decline with income. In addition, higher-income uninsured populations are likely to spend less time without insurance than lower-income populations are (Monheit and Schur 1988). This may further lower the propensity of higher-income people to take up a new policy made available to them. Two other studies also found higher price elasticities among lower-income people, but the differences are quite small (Marquis and Long 1995; RWJF 2000).

The availability of free care to low-income people suggests, however, that the observed price elasticity of demand for health insurance may increase with income, at least up to a point. In the RPA approach, the availability of free care increases reservation prices for low-income people (Pauly and Herring 2002). Another reason for a lower take-up by low-income people for certain types of programs is liquidity constraints, that is, those individuals who do not have enough money available to participate. Mainly for this latter reason, Gruber (2000) used a price elasticity that rises with income.

Unfortunately, no empirical evidence provides a good estimate for these adjustment factors. These factors have important policy implications because they affect our assessment of the relative efficiency of programs that target higher- and lower-income populations. Some modelers are quite explicit about how they model variation in price responsiveness, but in other models this variation is obscure. Policy analysts need to know not only the overall price elasticity of demand but also how that elasticity varies across specified populations.

Comparing Estimates with the Literature: Measuring Take-up by the Privately Insured

Another type of problem in assessing models is the difficulty of comparing simulation model assumptions with those in the existing empirical literature. This problem is well illustrated by the question of crowd-out.

In a world without inertia, every person would instantaneously switch to the form of insurance best suited to him or her. It would not be important to know whether or not he or she began with private insurance. Considerable evidence shows that people who currently carry insurance do tend to switch to cheaper coverage when it becomes available. This is almost certainly unavoidable because of the considerable job mobility in the economy. Even if a new public program contained a provision under which people were not permitted to drop private coverage (and this provision was enforced), people could still “drop” their coverage by changing jobs.

In practice, however, switching insurance coverage has a cost. Even free coverage is not universally taken up. At the same time, many people who qualify for free coverage continue to buy coverage individually or through their employer. Using the 1999 Current Population Survey, we estimated that of the 12.2 million American children under 15 who lived in a family with an income of less than 100 percent of the federal poverty level (FPL) and who were therefore income eligible for Medicaid, 1.9 million held employer-sponsored coverage, and more than 600,000 held individually purchased insurance. In the long run, we might expect people to move to less costly choices, but given the high rate of labor market mobility and income fluctuations in the economy, it is likely that the obstacles to obtaining the lowest cost plan will never be completely eliminated (unless a program were automatic). Thus, the take-up rate (or elasticity or reservation price) is likely to differ depending on an individual's initial coverage.

The empirical evidence on how responsive already-insured people are to a new program is found in the literature on crowd-out. Estimates of crowd-out generally refer to either the fraction of all those who take up a new program who had previously held private insurance or the decline in private insurance relative to total new program take-up (the two are equivalent if there are no newly uninsured as a consequence of the new program and if the same data are used).2

Unfortunately, these crowd-out measures are not the correct parameters for studies that simulate new health insurance expansions for which we have no prior experience. The crowd-out figures estimated depend on the size of the populations eligible for the program being studied and the degree to which this population is already insured. If a program affecting a different-size population with different insurance profiles is being simulated, the crowd-out estimate should be different.

A more useful way of thinking about crowd-out for simulation purposes is as a way of defining the relationship among take-up rates (or price elasticities) for different populations. The existing crowd-out literature provides some information about this relationship. While estimates of actual crowd-out differ substantially across studies that use different definitions of crowd-out, use different methods, and examine different populations, the implied ratio of elasticities turns out to be quite similar across studies.

Consider two groups, P and U, who hold private coverage and are uninsured, respectively, and who both will be eligible for a new program at a new price. Let the number of people who take up the new coverage from each group be T_p and T_u, respectively. Then crowd-out is defined as

The existing literature examines a Medicaid expansion where the new price is zero, so that all eligible populations will experience a 100 percent decline in the price they face for insurance. In this special case, the elasticity ɛ is just equal to the take-up rate

where P is the number who initially have private insurance and U is the number who initially are uninsured. Crowd-out can be rewritten as

which implies that

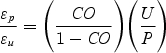Several studies of crowd-out in the Medicaid expansions yield parameters of these ratios. Note that these studies examine somewhat different subpopulations that face different prices. Cutler and Gruber (1996) estimated that P (the number of privately insured persons who would be eligible for the Medicaid expansion) is about 3.72 million; U is about 1.65 million; and CO is about 0.31.3 These estimates imply that the ratio of elasticities is about 0.20. Dubay and Kenney (1996) calculated that for the population below the poverty level, P is about 15 percent of the population, U is about 15 percent of the population, and CO is about 0.17, while for the population near poverty, the figures are 48 percent, 24 percent, and 0.22, respectively. These estimates imply that the ratio of elasticities is about 0.2. Thorpe and Florence (1998) estimated that for the population below 100 percent poverty in the National Longitudinal Survey of Youth (NLSY), P is about 22.3 percent; U is about 35.4 percent; and crowd-out is about 0.16. These estimates imply a ratio of elasticities of about 0.30.

Overall, the various studies suggest that for the privately insured, the elasticity of take-up of a new program is about 30 percent as high as the comparable figure for the uninsured. Note that this is true, even though the population that Cutler and Gruber (1996) studied had a much higher proportion of privately insured to uninsured people than did that in the Dubay and Kenney (1996) study and in the Thorpe and Florence (1998) study. The similarity in ratios implies that those features that make a program attractive to the uninsured in an income-defined population also make it attractive to the privately insured in that same population. Programs that make more people aware of a new insurance option, for example, should attract both uninsured and previously insured people.

The estimated figure, however, reflects only one particular experience (the Medicaid expansions). It would be useful to examine other programs and see whether the relationship between the two populations’ responses is similar. The general principle is likely to hold. When the take-up for one population increases, the take-up for another population rises as well. We recommend that modelers report how the insured respond to a program both in absolute terms and relative to how the uninsured respond. This will make it easier to compare crowd-out assumptions across models.

Ongoing Controversies

Some of the differences among the models arise from differences in the way that parameters are expressed or from deviations from the existing literature. Other differences, however, result when modelers disagree about assumptions in areas where the existing literature is quite thin. Two such areas important to policymaking today are firms’ behavior and decisions about taking up public or private coverage.

Firms’ Behavior

Most people with private insurance obtain it through their employers. Modeling crowd-out is thus closely linked to employers’ behavior. In response to a policy change, employers can choose to add, drop, or change contribution levels for coverage. Contribution levels, in turn, affect individual take-up decisions.

The Medicaid expansion experience provides limited information about employers’ behavior. Medicaid expansions targeted children and dependents under employers’ policies. Since employers cannot selectively drop coverage for only some employees, they are unlikely to respond to an expansion that targets only children of a limited number of employees by dropping coverage for all employees (Meyer, Silow-Caroll, and Wicks 1999). Broader expansions that also target adults can be expected to have a larger effect on firms’ behavior.

Economic theory suggests several possible models for how employers make offer decisions (Goldstein and Pauly 1976). All models suggest that employers take into account employees’ choices about trading off wages for benefits. The employer may do this with respect to the preferences of the marginal worker, the average worker (to minimize the total wage bill), the median worker (as in union-bargaining models), or some combination of workers.

The empirical literature on firms’ behavior is constantly changing. The existing empirical estimates of firms’ demand elasticity are all over the map, from a high of −5.8 (Feldman et al. 1989) to a low of −0.14 (Marquis and Long 1995). Several new studies have examined or are currently examining this question (e.g., see Blumberg and Nichols 2000; Finkelstein 2002; Gruber and Lettau 2000; Royalty 2000; Stabile 2002). In the new studies, most of the elasticity estimates cluster around −0.5 and are substantially smaller (often zero) for large firms than for small firms.

Employers’ responsiveness is a critical parameter in assessing alternative approaches to estimating the effects of health insurance expansions. Under some assumptions, some plans for expanding coverage could actually increase the number of uninsured persons, by leading many employers to stop offering coverage. Modeling employers’ responsiveness is difficult because it entails using information about the eligibility of individual workers within a firm as well as about both the firm's size and an aggregate profile of the firm's workers. Few data sets include all this information. Modelers are thus left with either making employers’ decisions based on the characteristics of the individual worker or developing a model of synthetic firms. The problem with the former approach is that it cannot capture the extent of interworker heterogeneity, which figures in employers’ decisions. The problem with the latter approach is that there is no one right, or even very good, way to do it.

It is important to recognize that the existing empirical and observational studies of firms’ offer decisions are based on small variations in the price of health insurance in the employer and individual market. Larger policy changes might cause a downward spiral in employers’ offering coverage. Some argue that an individual firm's decision may also reflect economywide practices, leading to the possibility that certain types of expansions could lead to a change in the norm of employers offering coverage. In particular, since employers (apparently) offer community-rated coverage to broad groups inside their firms, a decline in the number of employers that offer coverage could generate a selection spiral among those employers who continue to offer this benefit, by attracting the sickest employees to their firm.

Given both the uncertainty surrounding this parameter and its importance to policy, modelers should report it in a transparent fashion. Policy analysts and legislators should be made aware of the uncertainty surrounding this parameter and be encouraged to assess the validity of modelers’ assumptions about firms’ behavior. This is an area where sensible thinking should, at least for the moment, bear equal weight with the simulation model's output.

Another complex issue concerns the time scale. Most economic theory predicts the long run and often the very long run. Firms’ behavior in this regard is driven by the labor market, which can take many years to reach equilibrium. In contrast, some methods of estimating elasticity may estimate more short-run elasticities. Moreover, policymakers may be quite interested in the short run, so modelers should make clear the time scale they are modeling.

Taking up Public versus Private Coverage

Many of the most salient questions in expanding health insurance coverage today concern the choice between expanding public coverage or using tax credits for private coverage. In simulation models, this choice depends on how the take-up of public insurance compares with the take-up of tax credits. Few models, however, make clear how they treat this decision. The take-up probability for public insurance used in most studies for the population below 150 percent of the federal poverty level (FPL) is about 55 to 60 percent. This figure is drawn from many studies of public programs in the noncategorical population, which show average take-up rates in this range. How this compares with an elasticity depends on the model's parameters for a reduction in price to zero. A reduction in prices by 100 percent by Medicaid corresponds to a price elasticity of about −0.6 (Remler, Graff Zivin, and Glied 2002).

Some theoretical arguments imply that Medicaid take-up should be greater than tax credit take-up, but other theoretical arguments contend the reverse. If Medicaid stigma is important, Medicaid take-up should be lower than private take-up. Moreover, Medicaid incorporates retroactive eligibility. People may choose to wait until they are sick before taking up Medicaid coverage for which they are eligible. Private insurance is generally more difficult (or impossible) to obtain once people get sick. Since only a small fraction of the eligible population becomes sick, the take-up of private insurance might well exceed that of public coverage. Conversely, Medicaid eligibility determination decisions can be made more frequently than tax credit eligibility decisions. Signing up for Medicaid requires only one action, whereas tax credit take-up requires both purchasing coverage and claiming a credit.

Currently no empirical evidence sheds light on these differences. This makes it all the more important for modelers who examine tax credits or public program expansions or both to be very explicit and transparent about how they treat take-up and price responsiveness decisions. Even models of public programs that do not incorporate prices should report parameters in a way that can be compared with price responsiveness estimates.

Conclusion

The implementation of explicit budget targets has made budget forecasting even more important. The Congressional Budget Office's (CBO) scoring decisions can—at least in the view of policy analysts—make or break a policy proposal. For example, the Clinton administration's reform team devoted much effort to ensuring that the CBO would score their proposal positively—and so were rather disappointed with the results (Nichols 1995). In this climate, policy advocates and analysts will undoubtedly continue to devote considerable energy to these exercises.

Health insurance forecasting has always been imprecise. Early estimates of the premiums for the Clinton administration's health insurance proposal, for example, varied by about 35 percent (Rivlin, Cutler, and Nichols 1994). Errors in estimates of the cost growth of Medicaid and Medicare accounted for much of the CBO's overall budget forecast errors during the 1990s (Penner 2002). These errors are inevitable. As the long list in table 2 suggests, models require many assumptions; there are few data on which to base several of them; and many of the modeling decisions can generate differences among models. No simulation model can ever hope to be exactly right.

As Penner (2002) suggested, when examining the budget forecast process more generally, improvements in economic science are not likely to significantly improve the accuracy of estimates. But better reporting conventions could make it easier for policymakers to evaluate and compare estimates. Better reporting conventions would also help modelers improve their models and increase their credibility. This article is a first step in that direction.

A second step is to use the variation in models more effectively. For policy purposes, if the question is whether to undertake a health insurance expansion at all (instead of, say, a new policing program), it is most important to get an accurate assessment of one health insurance proposal. Given the considerable uncertainty surrounding estimates, this implies that one proposal should be estimated using many different models.

If the question is which health insurance expansion to undertake, it is most important to get an accurate sense of the relative behavior of these proposals. This implies that all proposals should be estimated using a single model. The reference case is a first step toward creating an even playing field for comparing proposals. Having all modelers use the consensus and best-guess assumptions prevents interested parties from “rigging” a simulation to get the predictions they favor. Where knowledge is not sufficient to mandate particular parameter assumptions for the reference case, reporting transparency will help educated consumers of simulations disentangle the extent to which predictions come from the policy proposal and the extent to which they come from the assumptions. In light of the variations among models, we should ideally compare the proposals using several models, all of which use the reference case framework and reporting standards. The differences in rankings and results across models could work like conventional cost estimates to bound the range of likely consequences.

Appendix: A Reference Case for Health Insurance Expansion Modeling

We propose that modelers adopt a set of conventions, which we call a reference case reference case, to report the results of simulation modeling. Our use of the term reference case reflects a similar effort to develop a prototype for cost-effectiveness analyses (Gold et al. 1996). As in that case, the reference case guides modelers describing their models and helps them better convey their information to policymakers. By adopting uniform reference conventions, modelers make it easier for policymakers to compare both models and the programs estimated by these models. At the same time, reference conventions should make more visible the uncertainty within models and the points of disagreement among them.

Modelers and policymakers may adopt the reference case conventions independently. In addition, policymakers and analysts should discount the results of any model whose parameters are not described in a clear, comprehensive, transparent, and comparable way.

We developed our reference case by searching the literature on health insurance expansions, comparing the existing models, and working with modelers at a meeting held in Washington, D.C., on January 11, 2001. However, although many modelers contributed to the discussion, this paper is not a consensus document.

The reference case described here has three types of elements. The first set consists of assumptions and parameters on which modelers substantially agree. We recommend that modelers who use these assumptions and parameters describe them as consensus assumptions (CA), to make it clear to readers that they have been agreed on. Modelers who choose to use other parameters might also consider reporting their results using the consensus assumption parameters for comparison.

The second set of parameters consists of those about which there is nearly irreducible uncertainty. We propose that in these cases, modelers adopt a set of “best-guess” baseline parameters that they then can use when initially calibrating their models. We recommend that modelers also describe their models’ predictions at defined sensitivity values for these parameters. We refer to them as best-guess

The third set of parameters and assumptions are those about which modelers disagree, based on theoretical or empirical evidence, about what the right values are. In these cases, it would be inappropriate to ask modelers to adopt any conventional values. Instead, the reference case approach asks modelers to describe these parameters in specific, consistent ways and provides a guide for doing so. By asking modelers to display in comparable terms the values they employ for uncertain parameters, the reference case should increase the transparency of the modeling results. We refer to them as reporting transparency (RT) parameters.

Prices and Premiums

Both measurement and conceptual issues arise when developing the base case for prices and premiums. We have only noisy information about existing prices and premiums. Our information comes from samples that may be nonrepresentative, limited to a portion of the market (often the nongroup market is excluded), or dated. In almost all cases, price and premium information is not adjusted for the generosity of observed benefit packages. An alternative to using price information is using information about loading costs. Unfortunately, this information is similarly incomplete. It may be biased by variations in insurer profitability (or the underwriting cycle) and in the practices of commercial insurers and Blue Cross insurers. Loading costs may vary over time. Finally, for some types of policy proposals, loading costs are not a sufficient statistic.

Ideally, regularly updated information on age-, sex-, health-, and region-adjusted rates for a standard benefit package in the individual and employer markets (according to a firm's size) would be available. (It soon may be possible to construct such rates using MEPS data available at the AHRQ data center, although there are nonresponse problems in the MEPS database.) Meanwhile, the reference case recommendation for insurance premiums is as follows:

• 1At the model's baseline, the sum of private health insurance premiums should correspond to its counterparts in the National Health Accounts. (BG)
• 2At the model's baseline, variations in premiums across age classifications, sex, market (nongroup versus group), and firm size should be reported for comparability. (RT)

A key conceptual issue with respect to premiums in the group market is incidence. Our recommendations with respect to incidence are the following:

• 3In the long run (defined as five to ten years, depending on economywide inflation assumptions), there is at least complete average incidence, although there is controversy over the degree of group-specific incidence. Modelers should report the extent of group-specific incidence they employ. (RT)
• 4In the very short run (defined as less than one year), there is zero incidence. (CA)
• 5There is zero incidence at the margin in large firms without cafeteria plans (i.e., if a particular employee drops coverage, that employee does not receive a wage increase). (CA)
• 6In cases other than these, modelers should define their assumptions concerning incidence by time period and firm size. (RT)

A second conceptual issue concerns the premiums for those who are uninsured at baseline. There is considerable controversy about what these premiums should be. For reporting simplicity only, we recommend the following:

• 7Modelers who choose not to use nongroup premiums as their baseline estimate for currently uninsured persons should clearly document their alternative assumption (e.g., the minimum of group and nongroup price). (RT)

Insurance Status

Defining the appropriate insurance status for all respondents at baseline is critical to a model's accuracy. This is an issue of measurement.

Different surveys of the population yield different estimates of the number of uninsured persons because of variation in survey questions, reference periods, and samples. In some cases (Medicaid, CHIP), there are specific, known problems with standard surveys. Despite these problems, the reference case recommendation is that

• 1Modelers should match their baseline numbers to the U.S. Census Bureau's counts of the uninsured. (BG)
• 2In sensitivity analyses, modelers should consider the effect of a 5 percent Medicaid undercount, drawn from the uninsured and privately insured in proportion to the representation of these sources among the population in the Medicaid-eligible income range. (CA)
• 3In sensitivity analyses, modelers should consider explicitly updating their baseline figures to reflect law and policy changes that have already been implemented but have not yet been captured in today's baseline data (e.g., the effect of CHIP expansions). (CA)

Another problem with insurance status is correctly modeling the health insurance unit (HIU) and tax-filing unit for eligibility purposes.

• 4Modelers should define HIUs according to a uniform definition. (CA)
• 5Modelers who do not use the HIU definition for tax-filing units should explain their alternative assumptions. (RT)
• 6Modelers should use explicit rules for defining health insurance units for people who receive health insurance from outside the household. (RT)

Eligibility

Modeling eligibility for existing and new programs is another area of measurement difficulty.

• 1When modeling baseline and program eligibility for uninsured persons, modelers should describe how they take into account non-income-related elements of eligibility. These include, at a minimum, earnings disregards, asset tests, and immigration status. (RT)
• 2When modeling current offer status for those persons without insurance, modelers should report their estimate of the proportion of all full-time, non- self-employed workers who have an offer and their estimate of the proportion of all uninsured people who have an offer in their HIU. (RT)

Individual Responsiveness

There are many different ways of modeling health insurance expansions. Each has a parameter, or a set of parameters, that defines how responsive insured and uninsured individuals are to a new coverage opportunity. There is a large empirical literature on this responsiveness, but there is also substantial disagreement about the correct magnitudes.

Ideally, estimates of responsiveness should have two properties. They should be identified from exogenous sources of variation in prices, and they should reflect the relevant heterogeneity within and characteristics of the population under consideration. Since data rarely offer both exogenous variation and an appropriate population, modelers should explain how they make this trade-off.

• 1Modelers who make their own estimates of responsiveness in conjunction with their modeling should describe the source of exogenous variation they use. If the model does not use exogenous variation, modelers should note the degree to which their responsiveness measure mirrors the literature. (RT)
• 2Modelers should clearly describe the degree to which the responsiveness measure they use reflects the population under consideration. (RT)

A substantial literature exists on the price elasticity of demand for health insurance, but the degree of variation in the literature also is substantial.

• 3The literature suggests that the price elasticity (for full price) for private insurance is in the range of −0.4 to −0.6. Modelers should report the elasticity estimate (or construct an elasticity equivalent if using a nonelasticity method) they use and justify it if using an elasticity estimate outside this range. Ideally, modelers should conduct sensitivity analyses within these parameters. (CA, RT)
• 4Price elasticity estimates in the published literature generally refer to the entire population, including those already insured. Modelers should make clear the population to which they are applying these estimates and describe how they adjust the estimates to compute price responsiveness in these populations (e.g., the uninsured). (CA, RT)
• 5Modelers should report (using an elasticity measure) the extent of price responsiveness they incorporate in their models for the population between 100 and 200 percent FPL. (RT)

There is very little information about how responsiveness varies with income.

• 6Modelers should report how their price responsiveness parameter varies with income. They should conduct a sensitivity analysis incorporating the assumption that price responsiveness does not vary at all with income. (RT)
• 7When reporting elasticity estimates for comparisons among models, modelers should use a price elasticity rather than a semielasticity. (RT)

There is more information about Medicaid take-up rates.

• 8The literature suggests that the take-up rate for public insurance expansions is in the range of 50 to 65 percent. Modelers should report the take-up rate estimate they use (or construct a take-up rate equivalent if using an alternative modeling method) and justify it if using a take-up rate estimate outside this range. Ideally, modelers should conduct sensitivity analyses within these parameters. (CA, RT)
• 9Modelers should describe, using an elasticity or take-up rate measure (noting clearly which), the take-up rate they expect for a public program at zero price for the population between 100 and 200 percent FPL. (RT)

Modeling assumptions about responsiveness should make sense for both public program expansions and for credit or voucher expansions.

• 10Modelers should describe their estimated take-up rate at zero price for the uninsured population 100 to 200 percent FPL for a private insurance expansion and should relate this figure to the Medicaid take-up rate parameter. (CA, RT)

Different assumptions are needed for people who are already insured.

• 11For programs that do not require beneficiaries to change their insurance source (e.g., take-up of tax credits for ESI by those with ESI), the estimated take-up rate in the literature is in the area of the EITC participation rate, about 85 percent. Modelers who use another assumption should justify it and, ideally, should conduct sensitivity analyses around this figure. (CA)
• 12For programs that do require beneficiaries to change their insurance source (e.g., public program expansions), modelers should report how the insured respond to the program both in absolute terms and relative to how the uninsured respond. (RT)
• 13Estimates of anti-crowd-out provisions should begin with a baseline of zero and consider the proposal's sensitivity to alternative parameters, unless an alternative assumption is clearly justified. (CA)

Employer Responsiveness

The literature on employer responsiveness is much less complete than that on individual responsiveness. Analysts agree that responsiveness is a function of the composition and size of the firm, but they disagree about how best to model this.

• 1The literature suggests that the price elasticity for firm offering for small firms is in the range of −0.6 to −1.8, and for large firms, 0 to −0.2. Modelers should report the elasticity estimate (or construct an elasticity equivalent if using a nonelasticity method) they use and justify it if using an elasticity estimate outside this range. Ideally, modelers should conduct sensitivity analyses within these parameters. (CA, RT)
• 2Modelers should clearly explain their decisions about changes in a firm's premium contribution rate. The decision rules for a firm's contribution should be consistent with the firm's add/drop rules. (RT)

Global Issues

• 1Modelers should clearly state to which year their estimates apply, both in calendar terms and for implementation of the expansion program. (RT)
• 2Modelers should use CBO estimates of economywide growth and inflation and CMS estimates of health care inflation. (BG)