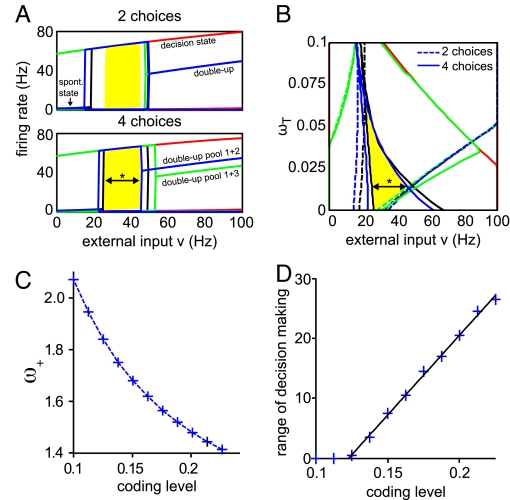
Fig. 4.
Common range of decision making for 2 and 4 alternatives in a mean-field approximation of the network. (A and B) For the parameters used in the spiking model simulations (except ωI = 1.1 instead of 1.125), the stable fixed points were calculated with the mean-field approximation over a range of external input ν from 0 to 100 Hz in steps of 0.5 Hz for the 2- and 4-choice condition and for 4 different initial conditions. Red, 1 pool starting at 120 Hz, the rest at 0 Hz; green, 2 opposite pools 30 Hz, the rest 0 Hz; blue, all 4 pools 30 Hz; black, all 4 pools 0 Hz. (A) Stable fixed points of firing rates of the selective pools (ωT = 0.015). In the decision state, exactly 1 pool is firing at a high rate, in the double-up state 2 pools. The traces of all other pools firing at low rates (≈2 Hz) overlap. For 4 alternatives, because all pools receive the input ν, there are 2 double-up states: one with neighboring pools (e.g., 1 + 2) firing at high rates, the other with opposing pools (e.g., 1 + 3) firing at high rates. In the 2-choice case, the input ν is applied only to 2 opposing selective pools (1 + 3), and thus only these pools will fire at high rates. The yellow region labels the range of decision making (see text) where the network is in the decision state for all initial conditions. (B) Starting and end points of decision states for the different initial conditions depend on the enhanced connectivity ωT between neighboring selective pools. Keeping the other parameters fixed, the value of the neighboring connectivity ωT with the optimal, i.e., broadest, range of decision making was determined by performing the fixed-point analysis explained above for ωT = 0 to 0.1 with steps of 0.0025. There is an optimal value of ωT for one parameter set, resulting in the broadest range of decision making (* black arrow); here, ωT = 0.015 (the value used in the spiking simulation and in A). (C) Dependence of the connectivity ω+ on the coding level f for constant fixed-point firing rates. To explore the relation between f and the range of decision making, the optimal value of ωT was determined for 11 different values of f from 0.1 to 0.225. When changing the coding level, the network connectivity has to be adapted to keep the up-state fixed-point firing rates at the same values. Thus, the connectivity value ω+ was adjusted in steps of 0.0025 until the up-state fixed points matched the values for the parameters of the spiking simulation (f = 0.2 and ω+ = 1.48, see A). For the ω+ values shown, the up-states deviated by less than 2 Hz in the 20- to 60-Hz range of external inputs, for the respective coding levels. Note that by changing ω+, the connections between the selective pools ω− change accordingly because of the normalization condition. (D) Optimal range of decision making increases linearly with the coding level. For each coding level, the optimal ωT was determined as shown in B, and the broadness of the yellow region, the range of decision making, was plotted against the coding level with a precision of 0.5 Hz. The black line is a linear fit to the data.