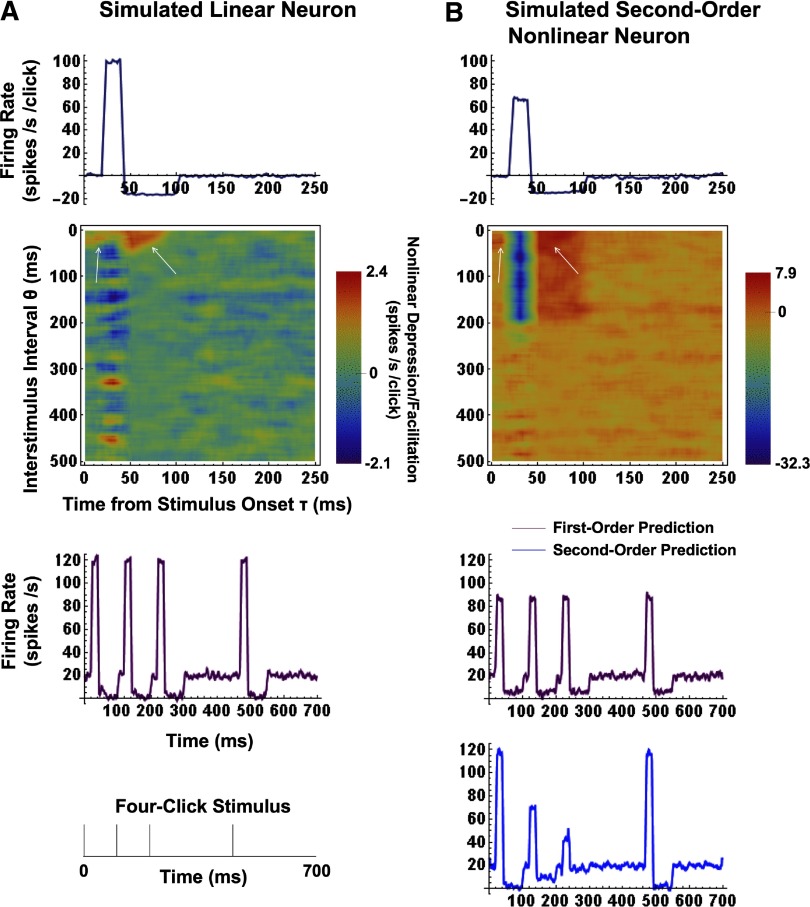
FIG. 1.

First- and 2nd-order Poisson-Wiener (PW) kernels and response predictions for a simulated linear and a 2nd-order compressively nonlinear neuron. A: 1st- and 2nd-order PW kernels (top) for a simulated linear neuron (see the text for simulation specifications). In the linear case, the 1st-order kernel is equivalent to the impulse response. The 2nd-order kernel illustrates the nonlinear depression and facilitation (by the blue and red ends of the color spectrum, respectively) of the impulse response due to interactions between pairs of impulses separated by time interval θ. Even the heavily smoothed (21 × 21-bin uniform filter) 2nd-order kernel is noisy, but has a mean value of 0 over any substantial vertical or horizontal strip for any linear neuron. Several artifacts due to the discrete computation appear in all 2nd-order kernels and are illustrated by white arrows. The 1st-order predicted response (purple curve) to a 4-click stimulus (bottom panel) is a very close match to simulation specifications. B: 1st- and 2nd-order PW kernels (top) for a simulated 2nd-order compressively nonlinear neuron (see the text for simulation specifications). In this case, the 1st-order kernel is smaller than the impulse response and so the 1st-order model (purple curve) underpredicts the response to single clicks (i.e., those with no preceding clicks in memory) but overpredicts the response to multiple clicks. The 2nd-order kernel characterizes and corrects for the compressive nonlinearity, so that the 2nd-order prediction (blue curve) is a very close match to simulation specifications.