Pre-tension generates strongly reversible adhesion of a spatula pad on substrate

Abstract

Motivated by recent studies on reversible adhesion mechanisms of geckos and insects, we investigate the effect of pre-tension on the orientation-dependent adhesion strength of an elastic tape adhering on a substrate. Our analysis shows that the pre-tension can significantly increase the peel-off force at small peeling angles while decreasing it at large peeling angles, leading to a strongly reversible adhesion. More interestingly, we find that there exists a critical value of pre-tension beyond which the peel-off force plunges to zero at a force-independent critical peeling angle. We further show that the level of pre-tension required for such force-independent detachment at a critical angle can be induced by simply dragging a spatula pad along a substrate at sufficiently low angles. These results provide a feasible explanation of relevant experimental observations on gecko adhesion and suggest possible strategies to design strongly reversible adhesives via pre-tension.

1. Introduction

This paper has been motivated by recent interests in understanding the robust and reversible adhesion mechanisms of the gecko, which appear to be both robust on a range of smooth to rough surfaces and at the same time easily releasable upon animal movement (Autumn et al. 2000, 2002, 2006a,b; Persson & Gorb 2003; Gao & Yao 2004; Hui et al. 2004; Gao et al. 2005; Glassmaker et al. 2005; Huber et al. 2005a,b; Spolenak et al. 2005; Tian et al. 2006; Yao & Gao 2006; Chen & Gao 2007a; Kim & Bhushan 2007; Peattie & Full 2007; Peattie et al. 2007; Chen et al. 2008; Gravish et al. 2008). It is widely believed that the secret of such robust and reversible adhesion lies with the gecko's hierarchical structures. The toe of Gekko gecko exhibits a lamella structure that contains millions of hairs called setae. Each seta is approximately 120 μm long and has a cross-sectional diameter of approximately 4.2 μm. The seta further branches into hundreds of spatulae through several shaft levels. At the very end of the branches, the spatula shaft holds a spatula pad that is 0.3 μm in length, 0.2 μm in width and 5 nm in thickness. It is an interesting scientific challenge to explore how such hierarchical structures enable both robust attachment and easy detachment on a rough surface.

The role of structural hierarchy in robust adhesion was investigated by Yao & Gao (2006) using a self-similar model with a ‘brush-on-brush’ type of multilevel hair structure. The model of Yao & Gao (2006) provided a basis to understand how structural hierarchy can lead to robust, flaw-tolerant adhesion, but it did not address the role of structural hierarchy in reversible adhesion. The latter issue was investigated together with the robustness issue by Chen et al. (2008) using a slightly different hierarchical model. At the level of a spatula, Chen et al. (2008) used Kendall's model of an elastic tape adhering on a substrate (Kendall 1975) to show that the pull-off force of a spatula pad could vary by an order of magnitude depending on the orientation of pulling. Based on this observation, it was shown that the variation in adhesion strength at the level of spatula leads to a two orders of magnitude variation in adhesion energy at the level of seta. Further going up in size scale, Chen et al. (2008) modelled the attachment of the gecko's toe to a surface as a thin elastic pad under displacement-controlled pulling and the detachment of the gecko's toe as a thin pad under peeling. It was shown that the attachment force can be much higher than the gecko's body weight while the detachment force can be negligibly small, indicating that the hierarchical microstructures on the gecko's toe can indeed enable robust attachment and easy detachment at the same time.

At the bottom level of structural hierarchy, the analysis of Chen et al. (2008) was based on modelling a spatula pad as a Kendall elastic tape. However, as pointed out by Autumn et al. (2006a), the Kendall model apparently failed to account for some of the important experimental observations. For example, Autumn et al. (2006a) reported that there exists a force-independent critical detachment angle for the gecko at widely different size scales, from an isolated seta to an array of setae to the entire toe of the gecko. Beyond this critical angle, apparently no adhesive force can be detected. If we trace these observations back to the level of spatula following the hierarchical model of Chen et al. (2008), one would deduce that a single spatula pad should also peel off at a critical angle independent of the applied force, even though the critical angle at the level of spatula need not be the same as that at the level of seta and above. Although Autumn et al. (2008) presented a phenomenological ‘frictional adhesion model’ to explain their observations, there is still no fundamental understanding on how a hierarchical adhesion structure might lead to a force-independent critical detachment angle. The fact that this phenomenon does not exist at all in Kendall's model is especially troubling, which suggests that some important factor might be missing in the existing studies so far.

To explain the experimentally observed force-independent detachment of the gecko at a critical angle, we note that the experiment by Autumn et al. (2006a) involves dragging the gecko's toe or isolated arrays of setae on a surface along the natural curvature of the seta before significant adhesion is detected and measured. We speculate that the dragging might have caused significant pre-tension to be built into the spatula pads as a gecko slides its feet against the surface, stretching the spatula while establishing contact. The hypothesis is that such pre-tension might be the missing factor that could explain the experimentally observed force-independent detachment of the gecko at a critical angle. To check this hypothesis, we consider in this paper a generalized Kendall model for a spatula pad in pre-tension adhering on a substrate and investigate in detail the effect of the pre-tension on the orientation-dependent adhesion strength of the spatula pad. We will show that the pre-tension generally tends to enlarge the peel-off force at small peeling angles while decreasing it at large peeling angles. More interestingly, we find that there exists a critical value of pre-tension beyond which the peel-off force plunges to zero at a critical detachment angle irrespective of the applied force, thus providing a feasible explanation of the experimentally observed force-independent detachment of the gecko at a critical angle. Further theoretical analysis and numerical simulation are conducted to show that the level of pre-tension required for the force-independent critical detachment can be generated by dragging a spatula pad on a surface at sufficiently low angles. We also note that, although this study is within the limitations of a small deformation, linear elastic model, the basic concepts remain valid even if the effect of large deformation is considered.

2. Generalized Kendall model with pre-tension

The problem of an elastic film with residual stress or pre-tension subjected to peeling from a substrate has been previously considered by Thouless & Jensen (1992), Williams (1993) and Kendall (1994). However, these previous studies were motivated by different physical considerations and none of them investigated the variation of the peel-off force as a function of the peeling angle at different levels of pre-tension. The adhesive contact between prestressed elastic spheres has been recently investigated by Chen & Gao (2006a–c, 2007b) within the frameworks of classical Johnson, Kendall and Roberts (JKR; Johnson et al. 1971) and Maugis–Dugdale (Maugis 1992) models.

In the following, we investigate in some detail the effect of pre-tension on the orientation-dependent adhesion strength of an elastic pad adhering on a rigid substrate, as shown in figure 1. The pad is assumed to be under plane-strain deformation with plane-strain Young's modulus E=2 GPa, Poisson's ratio v=1/3, thickness H=5 nm (Tian et al. 2006) and a unit width in the out-of-plane direction. Within the contact region of the interface, the adhesion is assumed to be governed by the van der Waals interaction energy of γ=0.01 J m⁻².

Figure 1.

An elastic thin film adhering on a surface subjected to a peeling force. The film resembles a spatula pad with plane-strain Young's modulus E=2 GPa, Poisson's ratio v=0.3 and thickness 5 nm. The system is under plane strain with a unit width in the out-of-plane direction. The adhesion energy across the contact interface is taken to be 0.01 J m⁻² and the theoretical strength of adhesion is 20 MPa.

2.1 Kendall's model

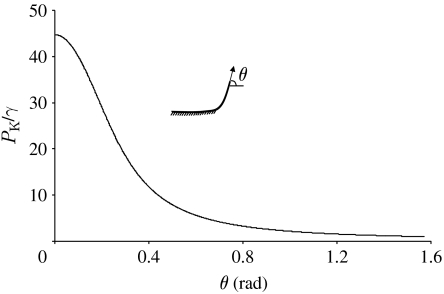
The inset of figure 2 shows an elastic thin film/pad on a rigid surface subject to a peeling force applied at an angle θ. For this problem, the critical peel-off force was determined by Kendall (1975) as

$$P_{\text{K}}=\frac{2\gamma }{\sqrt{{(1-\text{cos}\theta )}^2+\frac{2\gamma }{EH}}+(1-\text{cos}\theta )}.$$ (2.1)

Figure 2 plots the peel-off force P_K as a function of the peeling angle θ according to equation (2.1). We see that the lower the peeling angle, the larger the peel-off force. When θ=0, we find the maximum peel-off force as

$$P_{\text{K}}(\theta =0)=\sqrt{2EH\gamma }.$$ (2.2)

Figure 2.

Peel-off force of an elastic thin film/pad adhering to a substrate as a function of the peeling angle according to Kendall's model.

2.2 The generalized Kendall model

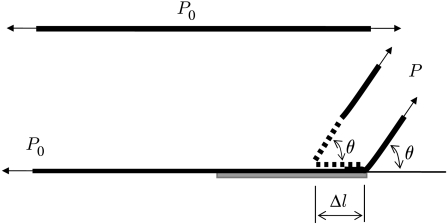
Now consider the problem of an elastic thin film/pad with pre-tension P₀ adhering on a rigid substrate as shown in figure 3. The pre-tension can be generated either as a residual stress in the film due to thermal or lattice mismatch between the film and substrate or by dragging the pad along the substrate at a low angle, as will be further discussed later in the paper. We are interested in how the pre-tension P₀ affects the critical force at peel off.

Figure 3.

An elastic thin film/pad with pre-tension is attached to a rigid surface and then subjected to peeling at an inclined angle.

The critical peel-off force P can be determined using the principle of virtual work. As the adhesion front is relocated by an infinitesimal virtual distance Δl (figure 3), the force P would translate in the direction of pulling by a distance of $\mathrm{\Delta }l(1-\text{cos}\theta )+\mathrm{\Delta }l((P-P_0)/EH)$, where the first term corresponds to the displacement that results from the detachment of Δl and the second term from the additional elastic deformation of Δl after it is detached. The work done by the applied peeling force is then

$$W_1=P\mathrm{\Delta }l(1-\text{cos}\theta )+P\mathrm{\Delta }l\frac{P-P_0}{EH}.$$ (2.3)

On the other hand, the change in energy of the system, including the surface energy and the stored elastic energy in the pad, is

$$W_2=\gamma \mathrm{\Delta }l+\frac{1}{2}\frac{\mathrm{\Delta }l}{EH}(P^2-P_0^2).$$ (2.4)

The energy balance W₁−W₂=0 at peel off provides the following critical condition:

$$\frac{P^2}{2EH}+P(1-\text{cos}\theta )-\frac{P{P}_0}{EH}+\frac{P_0^2}{2EH}-\gamma =0,$$ (2.5)

from which the peel-off force P can be determined as a function of the peeling angle θ at different levels of pre-tension P₀. It can be easily checked that equation (2.5) degenerates to Kendall's original model when P₀=0. A similar solution for a prestressed film under peeling can be found in Williams (1993).

For a given peeling angle θ, there are two roots to equation (2.5), corresponding to two branches of solutions P₁ and P₂. Without loss of generality, we rank them as P₂<P₁. For example, when θ=0, the two roots are

$$P_2=P_0-\sqrt{2EH\gamma },P_1=P_0+\sqrt{2EH\gamma }.$$ (2.6)

For stable adhesion, the energy released associated with the virtual displacement Δl of the peeling front must be smaller than the increase in energy stored in the system, i.e. W₁−W₂<0. This corresponds to the condition that the left-hand side of equation (2.5) must take a negative value, suggesting that stable adhesion occurs only when the applied force lies between the two roots P₂<P<P₁. In the case of small pre-tension $P_0<\sqrt{2EH\gamma }$, or P₂<0, stable adhesion requires the applied force to be smaller than P₁, i.e. 0≤P<P₁. In the case of large pre-tension $P_0>\sqrt{2EH\gamma }$, we have both roots positive, i.e. 0<P₂<P₁, in which case stable adhesion is possible only when the applied peeling force falls between the two roots, P₂<P<P₁. In this case, it is interesting to note that the spontaneous detachment occurs both for very large peeling force P>P₁ and for very small peeling force P<P₂. The latter condition indicates that, in the case of very large pre-tension, a finite applied force is actually necessary to stabilize adhesion. To better understand how P<P₂ results in spontaneous detachment, we can look at the case when θ=0. In this case, if $P_0>\sqrt{2EH\gamma }$, the residual stress becomes high enough that the film would detach even in the absence of an applied force, i.e. P=0, according to equation (2.6). This is just an example of residual stress-induced failure.

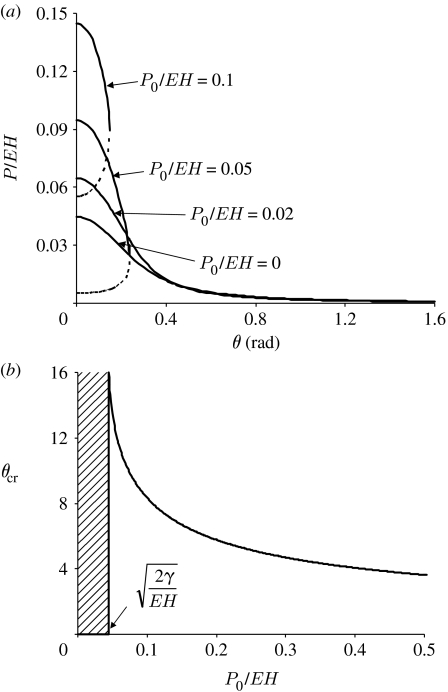
Figure 4a plots the positive roots of equation (2.5) for the predicted peel-off force P as a function of the peeling angle θ for different magnitudes of pre-tension P₀. In the case of P₂<0, only the positive root P₁ is displayed. In all cases, the upper root P₁ is plotted as solid lines while the lower root P₂ is plotted as dashed lines when it is positive and neglected when it is negative. The results show that the pre-tension generally tends to raise P₁ above that predicted by Kendall's model at relatively small peeling angles while decreasing it at large peeling angles. For relatively small pre-tension, such as the cases of P₀=0 and P₀=0.02EH in figure 4a, P₂<0 and P₁ sets the upper limit of the applied force before peel off occurs. For large pre-tension, such as the cases of P₀=0.05EH and P₀=0.1EH in figure 4a, we have two positive roots 0<P₂≤P₁, which merge into one solution at a critical peeling angle θ_cr. Stable adhesion occurs only within the region bounded by the two roots and it becomes impossible beyond the critical angle. In other words, the critical peeling angle θ_cr corresponds to the critical value of θ when equation (2.5) still has real solutions. When θ>θ_cr, equation (2.5) no longer has real solutions and the right-hand side of equation (2.5) remains positive for any applied force P>0. In this regime, we have W₁>W₂ for any applied force, indicating spontaneous detachment. Based on these considerations, the critical angle θ_cr is found to be

$${\theta }_{\text{cr}}={\text{cos}}^{-1}\left(1-\frac{P_0}{EH}+\sqrt{{\left(\frac{P_0}{EH}\right)}^2-\frac{2\gamma }{EH}}\right).$$ (2.7)

Figure 4.

Effect of pre-tension on orientation-dependent adhesion of an elastic thin film/pad adhering to a substrate. (a) Peel-off force of the film as a function of the peeling angle at different levels of pre-tension. The presence of a pre-tension generally increases the peel-off force at low peeling angles. Beyond a critical pre-tension, the peel-off force plunges at a critical peeling angle. Solid curves represent the upper branch of the critical peel-off force, and dashed curves represent the lower branch of the peel-off force when it is positive. (b) Variation of the force-independent critical detachment angle as a function of the pre-tension magnitude. The critical angle exists only when the pre-tension exceeds $\sqrt{2EH\gamma }$.

Figure 4b plots θ_cr as a function of P₀. It follows from equation (2.7) that θ_cr does not exist when $P_0<\sqrt{2EH\gamma }$, as can also be seen from figure 4b. This is consistent with the results shown in figure 4a, where the peel-off force P plunges at a critical angle when $P_0>\sqrt{2EH\gamma }$. Figure 4b shows that the critical angle θ_cr is usually approximately 5–15°. When θ<θ_cr, the upper root of the peel-off force has the expression

$$P_1=EH[-\left(1-\text{cos}\theta -\frac{P_0}{EH}\right)+\sqrt{{\left(1-\text{cos}\theta -\frac{P_0}{EH}\right)}^2-{\left(\frac{P_0}{EH}\right)}^2+\frac{2\gamma }{EH}}].$$ (2.8)

2.3 Effect of mode mixity

In adhesive contact mechanics models, it is often assumed that the adhesion energy is a material constant independent of the local failure mode, i.e. the adhesion energy does not depend on whether the detachment occurs by predominantly stretching or shear along the interface. The interfacial traction can in general be decomposed into a component normal to the interface and a component tangential to the interface. Borrowing a terminology from interfacial fracture mechanics (e.g. Hutchinson & Suo 1992), the normal component of the interfacial traction gives rise to a mode I stress intensity factor K_I and the shear component of the interfacial traction to a mode II stress intensity factor K_II. The mode-mixity angle defined as Ψ=tan⁻¹(K_II/K_I) can have significant impact on the critical peel-off force. Thouless & Jensen (1992) have derived the following expression for the mode-mixity angle associated with peeling an elastic pad with residual stress P₀:

$$\Psi ={\text{tan}}^{-1}\left[\frac{{\left({\text{sin}}^2\theta +2(1-\text{cos}\theta )/\left(\frac{P}{EH}\right)\right)}^{0.5}+\text{tan}\varpi \left(\text{cos}\theta -\frac{P_0}{P}\right)}{-{\left({\text{sin}}^2\theta +2(1-\text{cos}\theta )/\left(\frac{P}{EH}\right)\right)}^{0.5}\text{tan}\varpi +\left(\text{cos}\theta -\frac{P_0}{P}\right)}\right],$$ (2.9)

where ϖ is a scalar function depending on Dundurs' parameters for mismatch between the film and substrate (Suo & Hutchinson 1990). Note that the mode-mixity angle depends on the pre-tension, the peeling angle as well as the applied force.

It is known that the interfacial fracture toughness, defined here as the adhesion energy, can have a strong dependence on the mode-mixity angle (Evans et al. 1990), although the underlying mechanisms may vary for different materials systems. Different expressions of mode-mixity-dependent interfacial fracture energy Γ can be found in Hutchinson & Suo (1992). One such expression is

$$\Gamma (\theta )=\gamma /(1-\lambda {\text{sin}}^2\Psi ),$$ (2.10)

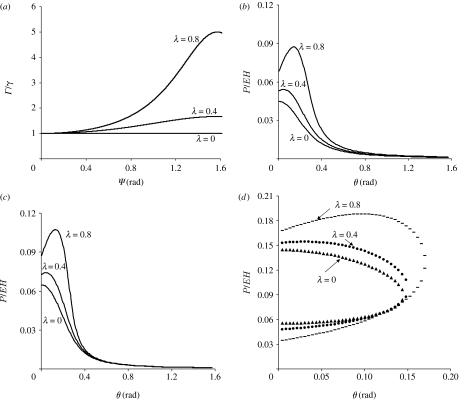
where Ψ depends on the peeling angle according to equation (2.9) and λ is a parameter ranging from 0 to 1. The adhesion energy defined this way is a constant independent of the mode-mixity angle Ψ when λ=0, but becomes increasingly dependent on Ψ as λ increases towards 1. Figure 5a plots the function Γ(Ψ) for different values of λ.

Figure 5.

Effect of mode mixity on orientation-dependent adhesion of an elastic thin film/pad adhering to a substrate. (a) Variations of the mode-mixity-dependent adhesion energy in equation (2.10) for different values of the parameter λ. The peel-off force of the film for different values of the mode-mixity parameter λ when (b) P₀/EH=0, (c) P₀/EH=0.02 and (d) P₀/EH=0.1.

When the adhesion energy varies with the peeling angle via equation (2.10), the critical condition in equation (2.5) for determining the peel-off force is modified as

$$\frac{P^2}{2EH}+P(1-\text{cos}\theta )-\frac{P{P}_0}{EH}+\frac{P_0^2}{2EH}-\Gamma (\theta )=0,$$ (2.11)

where γ in equation (2.5) has been replaced by Γ(θ).

Simple analytical solution to equation (2.11) is not available. Numerical solutions to equation (2.11) are displayed in figure 5b–d for different values of the pre-tension P₀/EH=0, 0.02, 0.1. In all calculations, we assume that the substrate is elastic with Young's modulus of 10 GPa and Poisson's ratio of 1/3, in which case ϖ=55.5°. We found that use of even higher values of Young' modulus for the substrate, e.g. approximately 70 GPa for glass, does not change ϖ significantly. The results show that the effect of mode mixity further enhances the adhesion strength at low peeling angles. Overall, the results in the case of a mode-mixity-dependent adhesion energy are qualitatively similar to that in the case of a constant adhesion energy. When the effect of mode mixity is taken into account, the effect of pre-tension still tends to enlarge the peel-off force at small peeling angles while decreasing it at large peeling angles. Also, similar to previous discussions, there exists a critical magnitude of pre-tension beyond which the peel-off force plunges to zero at a critical peeling angle, resulting in force-independent detachment at the critical angle. Below this critical angle, adhesion is stable when the applied force varies between two positive roots of equation (2.11). Above the critical angle, no stable adhesion is possible and detachment is spontaneous irrespective of the applied force.

3. The origin of pre-tension

We have shown in §2 that pre-tension can play a critically important role in the orientation-dependent peeling strength of a spatula pad on substrate. An open question is how such pre-tension might be generated in a spatula pad. For an elastic film on substrate, there exists in general a residual stress due to thermal or lattice mismatch between the film and substrate (Thouless & Jensen 1992). Here, we consider the possibility that the pre-tension may be generated by sequential attachment of an elastic pad to a surface when it is dragged along the surface at a low angle.

Kendall (1978) studied a thin film of rubbery polymer being peeled away from a glass surface at a low angle of approximately 5°, and observed that the peeled part of the film could jump back and reattach to the surface as a consequence of attractive interactions between the separated surfaces, causing a local healing of the detached region near the adhesion front. As a consequence of this healing, the peel-off force was found to be much higher than that predicted from equation (2.1). Kendall (1978) proposed an interfacial dislocation theory to explain this phenomenon. Here we generalize the observation and the corresponding theory of Kendall (1978) as a possible explanation for the origin of pre-tension in a spatula pad. We suggest that, when a spatula pad is dragged along a surface below a critical angle θ_K, Kendall's interfacial dislocations that result from local healing near the adhesion front are in fact equivalent to the generation of a large pre-tension by low-angle dragging. This process can in fact result in a very large pre-tension in the spatula pad.

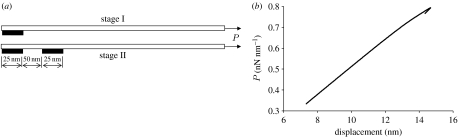
We first demonstrate the process of generating a pre-tension by local attachment of surfaces as a spatula pad is dragged along the surface at a very low angle. For this purpose, we consider a case in which attachment occurs sequentially at two neighbouring contact sites between a spatula pad and a rigid surface. As the spatula pad is dragged along this rigid surface at a low angle near 0°, we let it first adhere to the contacting site on the left. Before the applied force reaches the peel-off limit, we let the pad attach to the second contacting site while the spatula pad remains under near 0° peeling. Abaqus/Standard is employed to simulate this process. The two contacting sites on the rigid surface are 25 nm in length and 50 nm apart from each other. The van der Waals interaction energy within the contact region is taken to be 0.01 J m⁻². Two-dimensional plane-strain solid elements and two-dimensional cohesive elements are employed to model the film and adhesive interaction, respectively. The constitutive response of the cohesive elements is defined in terms of a traction-separation law, and failure of the cohesive element is through progressive degradation of the material stiffness after the maximum of the nominal stress reaches 20 MPa, the strength of the van der Waals interaction. Evolution of the failure is based on an isotropic dependence of adhesion energy on the mode-mixity angle. Figure 6b shows the calculated force–displacement relationship during the sequential attachment process described above. The simulation shows that the final peel-off force is 0.8 nN nm⁻¹, which is twice of the value 0.4 nN nm⁻¹ predicted by equation (2.1). Interestingly, an almost doubling of the peel-off force was also observed in the experiments of Kendall (1978) when healing occurred once along the peeled part of a thin film of rubbery polymer on a glass surface.

Figure 6.

Finite-element simulation of sequential attachment of contacting sites as a thin film is dragged along a substrate at a very low angle. (a) Schematic of the simulation process. At stage I, the film adheres to the first contacting site on the left under near 0° dragging. Right before it begins to detach from the substrate, the detached part of the film becomes attached to the second contacting site. (b) The simulated force–displacement relationship for the sequentially attached film. The film now has a built-in pre-tension and the peel-off force of 0.8 nN nm⁻¹ is about twice that predicted from Kendall's model in the absence of pre-tension.

The above analysis confirms that significant pre-tension can be induced by the Kendall (1978) type of sequential attachment as a thin pad is dragged along a substrate. According to Kendall (1978), the local healing/attachment involves no elastic energy because the strain in the pad does not change as the surfaces become attached. Applying the principle of virtual work to this process, it can be shown that surface attachment can take place only when the change in potential energy of the load is less than or equal to the change in surface energy, which yields

$$P_0(1-\text{cos}\theta )\le {\gamma }^{\prime },$$ (3.1)

where γ′ denotes the surface attachment energy which can in principle differ from the surface adhesion energy (Kendall 1978).

On the other hand, since the length of a spatula pad is limited, the pre-tension should also be less than

$$P_0\le {\sigma }_{\text{s}}L,$$ (3.2)

where σ_s is the shear strength of the interface and L is the length of the spatula pad in contact with the substrate. In order to achieve force-independent detachment at a critical angle, we must be able to generate a pre-tension larger than the critical value of $\sqrt{2EH\gamma }$, i.e. the length of the spatula pad should be longer than

$$L\ge \frac{\sqrt{2EH\gamma }}{{\sigma }_{\text{s}}}.$$ (3.3)

If we take typical values as γ=0.01 J m⁻², σ_s=20 MPa, E=2 GPa and H=5 nm, the lower bound of L would be approximately 22 nm. In order to achieve the level of pre-tension required for the force-independent detachment at a critical angle, as observed by Autumn et al. (2006a), the spatula must be dragged along the substrate at an angle smaller than a critical angle given by

$${\theta }_{\text{K}}={\text{cos}}^{-1}\left(1-\frac{{\gamma }^{\prime }}{\sqrt{2EH\gamma }}\right)\approx {\left(\frac{2{\gamma }^{\prime 2}}{EH\gamma }\right)}^{1/4}.$$ (3.4)

If we take γ′=0.3γ, the critical dragging angle is predicted to be θ_K=6.6° according to equation (3.4). Therefore, very low angles of dragging are indeed required to generate sufficiently large levels of pre-tension required for a preset detachment angle.

In addition to generating pre-tension by dragging its feet during attachment, it has also been observed that the gecko hyperextends its toes during detachment (Autumn et al. 2006b). It is possible that the hyperextension also helps generate additional pre-tension in the gecko's attachment pads to facilitate the detachment process. Further studies in this direction will be left to future work.

4. Discussion

The theoretical and numerical analyses presented in §§2 and 3 suggest that pre-tension induced by low-angle dragging of a spatula pad along a substrate may provide a feasible explanation of the experimental observations of Autumn et al. (2006a) who observed that dragging along the natural curvature of setae is actually necessary to generate sufficient adhesion at widely different scales ranging from single seta, seta arrays and the gecko's toe. These authors also found that the ratio of the shear reaction force to the normal force remains almost constant, although the magnitude of the force varies. It was also reported that a live gecko, when hanged on a single toe, detaches at a constant angle regardless of the body weight (adjusted by adding different weights on the gecko). As discussed by Autumn et al. (2006a), these observations cannot be explained by Kendall's (1975) model that would predict that the peel-off force should decrease smoothly as the peeling angle increases, as shown in figure 2. To explain their experimental findings, Autumn et al. (2006a) proposed a phenomenological frictional adhesion model, which was also adopted by Tian et al. (2006) in modelling the adhesion of a spatula pad. Tian et al. (2006) assumed that there is a sinusoidal variation of interaction energy along the interface, which provides a large magnitude of static friction force between the spatula pad and the underlying surface. Tian et al. (2006) then employed a force balanced criteria instead of an energy criteria to derive the adhesion force at different peeling angles. It is presently not clear how the model by Tian et al. (2006) is connected to classical contact mechanics models such as JKR (Johnson et al. 1971) and Kendall (1975) which are all based on energy criteria.

Our analysis presented a possible reconciliation of Kendall's model and the experimental findings of Autumn et al. (2006a) by incorporating the effect of pre-tension in the system that seems to have been overlooked in the existing literature on gecko adhesion. The experimental result by Kendall (1978) already indicated that local healing along the peeled parts of a polymer film at a very low angle with respect to the substrate can dramatically enlarge the peel-off force. Based on Kendall's finding, our present analysis indicated that the low-angle dragging of a spatula pad can lead to a level of pre-tension large enough to induce a critical detachment angle irrespective of the magnitude of the peel-off force, in agreement with the experimental findings of Autumn et al. (2006a).

We have shown that the generalized Kendall model incorporating the effect of pre-tension generally predicts larger peel-off forces, depending on the magnitude of pre-tension, at small peeling angles and smaller peel-off forces at large peeling angles compared with the corresponding predictions from Kendall's (1975) original model. These results seem to be consistent with the experimental findings of Autumn et al. (2006a) that different magnitudes of the peel-off force exist at a similar peeling angle when isolated setae or seta arrays are dragged along their natural curvature.

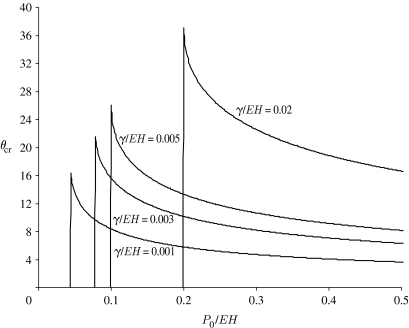
Our analysis also shows that there exists a critical pre-tension beyond which the peel-off force plunges at a critical angle of detachment, as shown in figures 4a and 5d, resulting in the force-independent detachment at a critical angle. This result may explain why a live gecko toe tends to detach at a critical angle irrespective of the magnitude of the applied force (Autumn et al. 2006a). However, the critical angle for spontaneous detachment from our analysis is smaller than the experimentally observed angle of approximately 25° in Autumn et al. (2006a). According to equation (2.7), we note that this critical angle depends on γ/EH. In the analysis above, we have taken γ=0.01 J m⁻², E=2 GPa and H=5 nm so that γ/EH=0.001. We find that the critical angle generally increases with γ/EH. For example, when γ/EH=0.005, the critical angle becomes 26°, as shown in figure 7. This result is consistent with the experimental observation that softer fibrillar structures tend to exhibit higher critical angles while stiffer fibrillar structures have lower critical angles (Schubert et al. 2008). Persson & Gorb (2003) suggested that the thickness of a spatula pad is approximately 5–10 nm, while we have taken it to be the lower bound of 5 nm in our analysis. For such a thin structure, the stored energy in the spatula pad is mainly due to stretching instead of bending. The van der Waals adhesion energy is typically between 0.01 and 0.05 J m⁻². Therefore, the value of γ/EH=0.001 used in our analysis represents a lower bound, while the upper bound can be as high as γ/EH=0.01. It seems that the discrepancy between the prediction from our analysis and the experimental observation of Autumn et al. (2006a) may be understood from the point of view that the adhesion energy of a spatula pad on the polar surface of glass tends to be on the high end value near 0.05 J m⁻².

Figure 7.

The critical angle for spontaneous detachment of an elastic thin film/pad adhering to a substrate as a function of the dimensionless parameter γ/EH.

Possible fracture of the contact from the sides of the spatula driven by Poisson contraction is another interesting issue. However, this mode of fracture is expected to be stable as its associated energy release rate will tend to decrease as the side cracks grow towards the middle. Thus, the net effect of such side cracking is to change the effective contact width between the spatula and the substrate, without affecting any of the conclusions in our paper.

It is worth mentioning that strongly reversible adhesion associated with friction has also been observed in synthetic fibrillar adhesives (Santos et al. 2007; Schubert et al. 2008). Although the detailed mechanism of such frictional adhesion may differ from that of the gecko, the basic principle that friction can induce strong orientation dependence of adhesion strength by building-in pre-tension in the fibrils may still be applicable in synthetic fibrillar adhesives.

5. Conclusion

We have shown that Kendall's (1975) model of an elastic film adhering on a substrate can be generalized to incorporating the effect of a pre-tension in the film. This generalized Kendall model is then employed to investigate the effect of pre-tension on the orientation-dependent adhesion strength of a spatula pad on substrate. Our analysis indicates that the pre-tension can significantly enlarge the peel-off force at small peeling angles while decreasing it at large peeling angles, resulting in strongly reversible adhesion. The peel-off force at higher pre-tension decreases much faster as a function of the peeling angle compared with that at smaller pre-tension. More interestingly, we find that the peel-off force can plunge at a critical angle when the pre-tension exceeds a critical value, resulting in force-independent detachment at a critical angle. We also find that large magnitudes of pre-tension, even those beyond the critical value required for the force-independent detachment at a critical angle, can be generated by dragging the spatula along the substrate at a sufficiently low angle. These results provide a feasible explanation for the relevant experimental observations of Autumn et al. (2006a). The present study also suggests possible strategies to design strongly reversible adhesives via built-in pre-tension in the system.