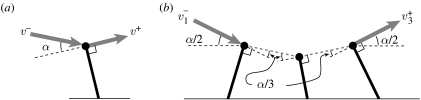
Figure 1.
Simple models illustrating how geometry dictates energy loss for (a) single and (b) multiple collision gaits. The velocity of the CoM is v, the body mass is m, the kinetic energy is E, the total angle of deflection (i.e. the angle between the incoming and outgoing velocity vectors) is α and the total number of collisions is n. The ‘minus’ and ‘plus’ superscripts indicate before collision and after collision values, respectively. The subscript i indicates the ith collision in a sequence involving multiple collisions. (a) For a single limb, the fraction of energy lost during a collision transition is given by ΔE/E−≈α2 for small angles; v+=v− cos α, E−=(1/2)m(v+)2, E+=E− cos2α, ΔE=E−−E+=E−(1−cos2α), ΔE/E−=sin2α≈α2. (b) For three legs in which the transition is evenly distributed between the legs, the fraction of energy lost for each collision is given by , because the angle for each collision is α/3. But there are three times as many collisions, so the total fraction of energy lost during the entire transition is (ΔE/E−)tot≈3(α/3)2=α2/3 or 1/3 of that lost for a transition mediated by a single limb. This can be extended to n legs where the total energy lost during a transition is given by (ΔE/E−)tot≈α2/n; , , , , , .