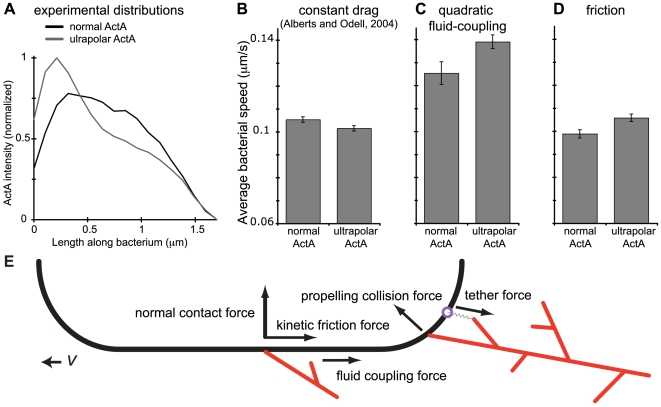
Figure 3. Ultrapolar bacteria move faster than normal ActA bacteria in simulations incorporating a cooperative restraining mechanism.

A) Representative examples of a normal ActA distribution and an ultrapolar ActA distribution selected from the experimental dataset for use in the simulation. These distributions are scaled such that the total amount of ActA is equal. B) Representative set of simulation runs with normal and ultrapolar ActA distributions for simulations exhibiting a constant drag as in [12]. Regardless of the parameters chosen, the normal ActA bacteria always moved faster than the ultrapolar bacteria. In this particular set of runs, the average speed of the normal ActA and ultrapolar bacteria was 0.101 and 0.105 µm/s (n = 20 simulation runs for each distribution.) Average speeds were significantly different by rank sum analysis (p-value 0.038). C) Simulations runs with the identical parameters as in B but incorporating fluid coupling of the bacterium to the surrounding filaments with a quadratic dependence on filament number. Now the ultrapolar bacteria move more rapidly than the normal ActA bacteria (0.139 and 0.125 µm/s respectively, n = 15). Average speeds were significantly different by rank sum analysis (p-value 0.028). However, we cannot physically justify this quadratic fluid coupling (Fig. S2). D) Simulation runs with the identical parameters as in B but incorporating a frictional force between actin filaments and the bacterial surface. Ultrapolar bacteria move more rapidly than the normal ActA bacteria (0.106 and 0.099 µm/s respectively, n = 20). Average speeds were significantly different by rank sum analysis (p-value 0.005). This particular set of runs used a friction coefficient of 0.2. However these results were robust to changes in simulation parameters, e.g. for 6-fold higher friction coefficients and for simulations with increased actin tail densities (data not shown). Error bars are standard error. E) A schematic definition of the forces in the simulation shown on half the surface of a 2D capsule shaped bacterium. Any collision between a filament and the bacterial surface defines a contact force, assumed normal to the bacterial surface regardless of filament orientation. The collision may be the result of thermal motions of the bacterium and actin structures, or a filament may polymerize ‘into’ the bacterium. Bonds between actin filaments and surface bound ActA proteins can lead to a tether force if that bond is strained. This protein-protein tether is distinguished from the smaller scale forces between electrically charged molecules that lead to kinetic friction. A shape-based viscous drag is assumed for all bodies in the simulation, but that drag might be modified to account for the fluid-coupling between bodies. To include this fluid-coupling between actin filaments and the bacterium we increase the bacterial drag as a linear function of the surrounding filament population.