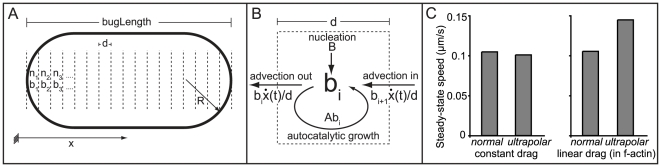
Figure 5. A one-dimensional barbed-end tracking model of L. monocytogenes motility.
A) The bacterium is spatially discretized into 0.1 µm long mesh elements along the long-axis (the x-direction). In each of the mesh elements, two state variables 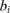 and
and 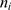 –the number of barbed-ends and the f-actin density, respectively– determine the element contribution to propulsion force and drag coefficient. B) Equations for
–the number of barbed-ends and the f-actin density, respectively– determine the element contribution to propulsion force and drag coefficient. B) Equations for 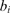 , for example, are derived from conservation of barbed ends at a single mesh element:
, for example, are derived from conservation of barbed ends at a single mesh element: 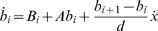 , where
, where 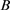 is the nucleation of new barbed-ends (i.e. a new mother filament),
is the nucleation of new barbed-ends (i.e. a new mother filament), 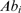 is the autocatalytic creation of barbed-ends from existing barbed-ends (i.e. branching), and
is the autocatalytic creation of barbed-ends from existing barbed-ends (i.e. branching), and 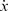 is the velocity of the bacterium. Only elements on the hemispherical cap significantly contribute to propulsion force, while f-actin along the side of the bacterium contributes to the drag force. The ratio of force to drag determines the instantaneous velocity
is the velocity of the bacterium. Only elements on the hemispherical cap significantly contribute to propulsion force, while f-actin along the side of the bacterium contributes to the drag force. The ratio of force to drag determines the instantaneous velocity 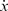 . A similar element diagram can be drawn for
. A similar element diagram can be drawn for 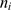 , though without any autocatalytic term. C) Steady state speeds for different ActA distributions. A constant drag on the bacterium led to faster normals than ultrapolars. Incorporation of a linear filament-dependent restraining mechanism, representing either (or both) filament-surface tethers or fluid coupling led to faster ultrapolars than normals, as in our experimental observations. A cooperative filament-dependent restraining mechanism (representing kinetic friction, for example) similarly led to faster ultrapolars (data not shown).
, though without any autocatalytic term. C) Steady state speeds for different ActA distributions. A constant drag on the bacterium led to faster normals than ultrapolars. Incorporation of a linear filament-dependent restraining mechanism, representing either (or both) filament-surface tethers or fluid coupling led to faster ultrapolars than normals, as in our experimental observations. A cooperative filament-dependent restraining mechanism (representing kinetic friction, for example) similarly led to faster ultrapolars (data not shown).