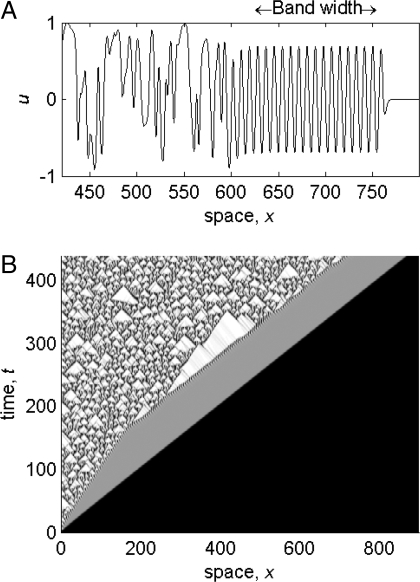
Fig. 1.

A numerical simulation of invasion in Eqs. 1, for ω₀ = 3.1, ω₁ = 3.0. At time t = 0, a small perturbation is applied near x = 0 to the unstable steady state u = v = 0. An invasive wave front spreads across the domain (at speed c _inv = 2), behind which is a wavetrain band of constant width, followed by spatiotemporal disorder. (A) u vs x at t = 385. (B) A space–time plot of amplitude r (darker shading indicates smaller r, 0 < r < 1). The boundary conditions are u _x = v _x = 0 at x = 0,900. Our numerical method is semiimplicit finite difference, with grid spacing of 0.18 and a time step of 10⁻³.