Pattern Selection in Plants: Coupling Chemical Dynamics to Surface Growth in Three Dimensions

Abstract

Background and Aims

A study is made by computation of the interplay between the pattern formation of growth catalysts on a plant surface and the expansion of the surface to generate organismal shape. Consideration is made of the localization of morphogenetically active regions, and the occurrence within them of symmetry-breaking processes such as branching from an initially dome-shaped tip or meristem. Representation of a changing and growing three-dimensional shape is necessary, as two-dimensional work cannot distinguish, for example, formation of an annulus from dichotomous branching.

Methods

For the formation of patterns of chemical concentrations, the Brusselator reaction-diffusion model is used, applied on a hemispherical shell and generating patterns that initiate as surface spherical harmonics. The initial shape is hemispherical, represented as a mesh of triangles. These are combined into finite elements, each made up of all the triangles surrounding each node. Chemical pattern is converted into shape change by moving nodes outwards according to the concentration of growth catalyst at each, to relieve misfits caused by area increase of the finite element. New triangles are added to restore the refinement of the mesh in rapidly growing regions.

Key Results

The postulated mechanism successfully generates: tip growth (or stalk extension by an apical meristem) to ten times original hemisphere height; tip flattening and resumption of apical advance; and dichotomous branching and higher-order branching to make whorled structures. Control of the branching plane in successive dichotomous branchings is tackled with partial success and clarification of the issues.

Conclusions

The representation of a growing plant surface in computations by an expanding mesh that has no artefacts constraining changes of shape and symmetry has been achieved. It is shown that one type of pattern-forming mechanism, Turing-type reaction-diffusion, acting within a surface to pattern a growth catalyst, can generate some of the most important types of morphogenesis in plant development.

INTRODUCTION

The issue of how plants and other organisms with cell walls achieve their shapes is a very complex problem, which will ultimately require a synthesis from many disciplines, including molecular and cell biology, biophysics and physical chemistry. The present study investigates the interplay between the pattern formation of growth catalysts on plant surfaces and the expansion of those surfaces to generate organismal shape. Although an enormous amount of information has been gained in recent years on the molecules involved in patterned growth, especially in higher plant model systems (e.g. Cosgrove, 2005; Ingram and Waites, 2006; Anastasiou and Lenhard, 2007; Beveridge et al., 2007), the broader issues of how these molecules are localized, what maintains localization upon growth and how growth symmetries are broken remain far less explored. While some simpler types of morphogenesis, such as extending tip growth, may arise from a particular asymmetry in growth that is perpetuated, many morphogenetic sequences involve repeated symmetry-breaking, for example repeated branching tip growth from a tip or shoot apex. Selection of different patterns over the course of development requires that not only must the chemistry direct growth, but also that the chemistry must respond to growth (and geometry) such that appropriate pattern is generated or maintained.

The focus herein is on the chemical dynamics and constraints required for this feedback, to find principles of kinetics and transport underlying morphogenesis. Recently, there has been a great deal of work in modelling reactions and transport in the apical meristems of higher plants (Jönsson et al., 2006; Prusinkiewicz and Rolland-Lagan, 2006; de Reuille et al., 2006; Smith et al., 2006; Heisler and Jönsson, 2007), giving new insight into how these processes create pattern in these systems. To focus on the growth-patterning feedback, however, we find it helpful to apply physicochemical modelling to morphogenesis in simpler systems, such as unicellular green algae. Many genera create body architectures as complex as higher plants, but in a single cell with a continuous surface. In these cases, pattern formation is not cell-specific gene expression, but rather spatial concentration patterns in the same plasma membrane. Removing the complexities of multicellular tissues makes these ideal for studying the chemical dynamics or biophysics of morphogenesis. Across higher plants and algae, there may be different mechanisms of surface expansion, including localized wall loosening by expansins (e.g. Cosgrove, 1996; Fleming et al., 1997) or localized delivery of wall material (intussusception; see Bonner, 1934). However, the overall constraints on growth rates and patterning boundaries to generate coherent form are greatly shared in all organisms, unicellular or multicellular, in which the parts of the growing surface do not change their relative positions after formation, i.e. in which there is no phenomenon such as cell migration as seen in animals.

This paper presents the results of a computational investigation of a surface chemical pattern-forming mechanism that drives surface expansion and is capable of breaking symmetry, for the transition between types of shapes. The model consists of fairly generic reactions, such as activation and inhibition, and transport, which could be applied to most regulatory networks. This allows us to couple a minimal pattern-forming mechanism with growth, and to explore the limits of the chemical contribution to shape formation. Plant shape ultimately relies also on the mechanical properties of cells (e.g. Pelce and Sun, 1993; Kam and Levine, 1997; Green, 1999; Dumais et al., 2006; Dumais, 2007); this study does not directly account for the mechanical response to surface expansion, but rather focuses on the primary process of chemical catalysis of expansion of area, leading to shape change that reduces mechanical stress to zero by moving enlarged elements of area outwards until there is just sufficient space to accommodate them. This work complements the molecular biology approach, by providing a framework for how form and chemistry must interact to give observed morphogenetic sequences.

Plants develop by growth and pattern formation in separate, localized small regions (e.g. meristems) that remain roughly constant in size as the plant grows. The study describes the dynamics necessary for a chemical patterning mechanism both to maintain pattern in a growing system and to give the transitions between patterns necessary for complex morphogenesis. The key is for there to be a mechanism in the chemistry that sets up regions of fast and slow growth. The resulting differences in growth rates create distinct domains of active growth, and translate chemical pattern into distinct shape.

The present project builds on more than 20 years of work. We first explored the coupling of chemical patterning to domain growth in Harrison and Kolář (1988), in which a Brusselator chemical pattern-forming mechanism (Prigogine and Lefever, 1968) catalysed growth of line segments of a closed loop, leading to shape change in a two-dimensional (2-D) plane, i.e. tangential surface increase is accommodated by normal displacement. As mentioned above, this does not take into account mechanical anisotropies or shearing, but directly models the simplest shapes accommodating localized surface expansion due to chemical pattern. We contrast this with accretive (crystalline) models of cellular growth (Denet, 1996). This project was the first work in which chemical patterning and growth were fully linked in a feedback cycle. Earlier work had studied the effect of domain growth at an arbitrary uniform rate on patterning, but without the patterning having any effect on growth (Harrison et al., 1981; Meinhardt et al., 1998). More recently, there have been experimental (Miyakawa et al., 2000) and theoretical (Crampin et al., 2002; Salazar-Ciudad and Jernvall, 2004; Boissonade, 2005; Neville et al., 2006; Yashin and Balazs, 2006) studies involving full feedback between patterning and growth. Key to all these studies is that reaction-diffusion mechanisms such as the Brusselator have a pattern wavelength that depends on rate constants and diffusivities (Turing, 1952). As a domain grows, therefore, more of the concentration peaks can be observed, unless some feedback suppresses new peaks.

There are two types of very large unicellular algae that together display pattern changes relevant to some of the most important features of multicellular plant development. First, the Dasycladales, an order of marine algae that have been described as ‘the most improbable unicellular organisms that exist’ (see Berger and Kaever, 1992, for this quotation and a comprehensive description of the order). Particularly, for our topic of pattern formation, they form whorled structures at a growing tip, demanding three dimensions in computational work on patterning mechanisms (see Harrison et al., 1981, for a primitive start). Second, among the common and widespread freshwater placoderm desmid algae, the genus Micrasterias is unique in displaying sequences of successive dichotomous branchings of growing tips.

Species within the genus Micrasterias provide a wealth of diverse forms to challenge any morphogenetic model (Fig. 1). In particular, we have been drawn to this genus (following Lacalli, 1973) because they display repeated symmetry-breaking, changing from tip growth to dichotomous branching, and morphogenesis largely occurs in the plane, allowing 2-D work as a starting place for modelling. One of the first discoveries of the Harrison and Kolář (1988) work was that a mechanism that can give branching chemical pattern does not manifest this into shape change, unless there is some means of segregating the branches from one another (as plants most commonly do). They developed a wall-ageing mechanism, in which slow-growing regions incorporated less and less wall material, and eventually shut off patterning. This allowed the model to account for extended tip growth and repeated branching.

Fig. 1.

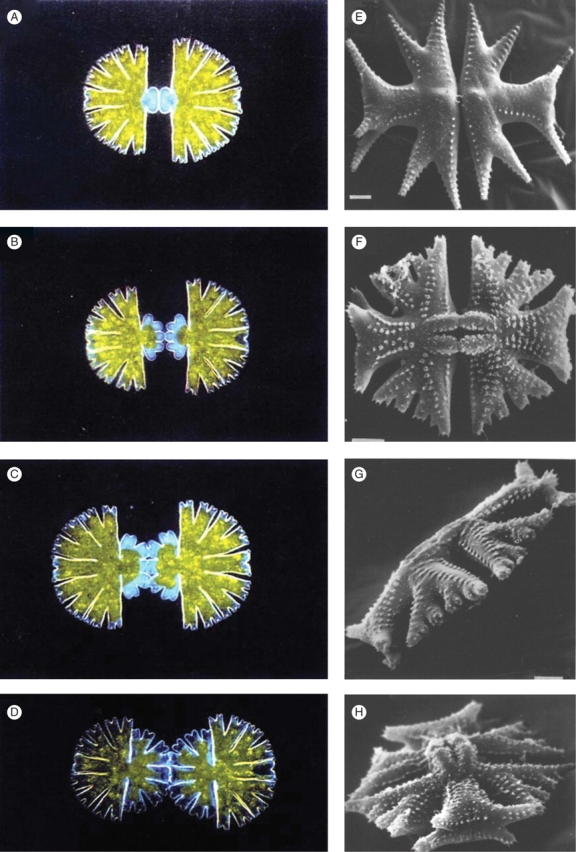
Morphogenesis in Micrasterias. (A–D) Developmental sequence in M. thomasiana. Mitosis gives two daughter cells, each with a mature semicell and a newly forming semicell (daughters are in physical, but not developmental, contact). Over the course of about 4 h, the new semicells undergo repeated dichotomous branching, to create the mature morphology. (E–H) Some of the diversity between different species in the genus. Note the distinct shapes of the central, polar lobes, and the lateral, wing lobes. In particular, the second branch of the polar lobe is out-of-plane with the rest of the cell body; maintenance of the branching plane is far more controlled in the wing lobes, with out-of-plane branching generally occurring after many (4–5) branching events. E–H from Couté and Tell (1981) with permission.

This mechanism, however, was not capable of generating the acute branching angle seen in most species of Micrasterias, and necessary for tackling any more wide-ranging explanation of branching in plants. This ended up requiring a faster shut-off of slow-growing regions, by introducing a feedback of the growth catalyst on its own production (Holloway and Harrison, 1999). With this feature, we were successful in modelling a wide variety of the diverse shapes found in Micrasterias. The key feature distinguishing species in our model was the threshold of growth catalyst necessary to cause growth. Variation of this threshold during development accounted for variation in branching number and branching angle, the chief distinguishing features between species.

A number of questions arose in our 2-D work, prompting us to move to three-dimensional (3-D) modelling. These include:

1. What constrains the clefts between growing tips? In two dimensions, it was necessary to arbitrarily fix the position of the surface on which patterning had ceased.

2. What makes Micrasterias planar? Why are the repeated dichotomous branchings all in the same plane, when the algae are free floating in their environment?

3. What defines the growth catalyst threshold? Our earlier work identified this as an important parameter for controlling shape; can we go further in understanding the chemical dynamics necessary to define and regulate this threshold?

4. The patterns, or symmetries, that can be realized in two dimensions are fairly constrained. In three dimensions, the options are much greater. For example, a simple dichotomous branch in a 2-D plane could be the same in three dimensions, or an annular flattened tip, or a whorl of structures, such as in a flower. What selects among these options, for particular developmental events?

To begin addressing these issues, we developed a 3-D version of our model (Harrison et al., 2001), with a surface specified by finite elements (rather than line segments). In this preliminary work, geometry alone – slow surface growth in the cleft at right angles to the fast growth of the tips – was found to be able to maintain cleft position ((1), above). However, repeated dichotomous branching in three dimensions gave alternating branching planes, unlike much of Micrasterias development. In this work, and that of Nagata et al. (2003), we also began to explore the selection of annular vs. dichotomous branching patterns ((4), above).

The present paper reports our subsequent progress. We have determined that geometric asymmetry is not sufficient for maintaining the Micrasterias branching plane, as earlier hypothesized (Harrison et al., 2001). Rather, a persistent chemical asymmetry in growth catalyst precursors is likely to be required. The possible patterns of these precursors on the surface shapes of developing Micrasterias may be responsible for the very different morphologies of the central, polar lobe and the lateral, wing lobes of the mature cell. The requirements for generating, maintaining and switching between the fundamental shapes of tip growth, tip flattening, tip re-initiation, dichotomous branching and whorls of 3–6 structures are also demonstrated. Finally, preliminary results are presented on controlling the boundaries between fast- and slow-growing regions through additional chemical dynamics, rather than through the threshold value of the growth catalyst.

In relation particularly to the dasyclads, but with relevance to any work on patterning in algae, Dumais and Harrison (2000) addressed the following question: ‘When a definitive identification of the pattern-forming event is reached, will it throw light on development of anything other than the dasyclads?… Some authors (e.g. Church, 1919; Chadefaud, 1952; Emberger, 1968) not only argued for a natural continuity between algae and higher plants [also see Lewis and McCourt, 2004], but also emphasized that algae account for all the major structural innovations in the plant kingdom… Mandoli (1998) and Nishimura and Mandoli (1992) have identified juvenile and adult developmental phases in Acetabularia closely corresponding to such phases in higher plants. Hagemann (1992) and Kaplan (1992) have also discussed general implications of similar development with and without multicellularity.’ For instance, our concentration on Micrasterias as an example of co-planar repeated dichotomous branching somewhat disguises a more general applicability of such work, to the telome theory of evolution in vascular plants (Zimmermann, 1952). Repeated dichotomous branching is central to this theory, and ‘planation’, i.e. co-planar arrangement of the successive branchings, is the second of Zimmermann's postulated transformations (for a most recent review, see Beerling and Fleming, 2007). Although this theory remains speculative, the theoretical study of successive dichotomous branching ensures that we are setting up a model in which, after a branching process, the new apices can retain the ability to branch repeatedly, as needed for planation or Micrasterias, or revert to dominance of the original apex, as is more common in higher plants. The results suggest the conditions underlying these differences.

MODELS AND METHODS

Chemical pattern-forming mechanism

For our minimal model giving spatial pattern formation, we use the Brusselator mechanism, originally developed by Prigogine and Lefever (1968):

1a

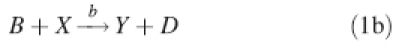1b

1c

1d

With diffusion of the X and Y intermediates, and appropriate rate constants a–d, this mechanism generates stable spatial patterns in the X and Y concentrations. For most of our modelling relevant to plant rather than animal development, we choose the Brusselator rather than other reaction-diffusion mechanisms (e.g. the Gierer–Meinhardt model) because the Brusselator dynamics are particularly good for generating patterns of multiple, equally spaced repeated parts (Lacalli, 1981; Harrison, 1993). The interactions of eqns (1b) and (1c), autocatalysis of X and de facto inhibition of X by Y (by depletion), are at the heart of the pattern formation, and represent commonly occurring motifs in biochemical networks. In many of our computations, a prepattern, or gradient, is introduced into the precursor A. This represents the result of an earlier stage of development, such as an initial polarization defining which side of a system is going to have the meristem or growing tip advancing out of it. We couple this mechanism to growth, by making the surface expand in proportion to the X concentration. A model for patterning regions that remain small and separate from regions of slower unpatterned growth requires an additional feature to account for the boundary between these regions. Here (as previously in Holloway and Harrison, 1999) this boundary is defined by a threshold X concentration, X_th, above which the pattern-forming reactions, eqns (1a)–(1d), operate, and below which only the decay of X, eqn (1d), does. From eqns (1a)–(1d), with Fick's law for diffusion in the surface, the following partial differential equations (PDEs) describe the time evolution of the X and Y concentrations:

2a

2b

where the D's are the diffusivities of X and Y, and ∇² is the Laplacian operator (in Cartesian coordinates, sum of 2nd spatial derivatives). In the unicellular examples, the diffusivities concerned are likely to be attached to the plasma membrane for molecular species, or in a cortical layer of cytoplasm. For multicellular plants, they could represent intercellular movement via plasmodesmata in the tunica layer (Holloway and Lantin, 2002). A wavelength, or spacing, for the X and Y patterns can be found (Turing, 1952), which depends on the rate constants a–d, input concentrations A and B, and diffusivities D_X and D_Y. At first emergence of pattern from uniformity, the incipient patterns of X and Y concentrations mimic the harmonic patterns of displacement in mechanical vibrations of thin shells. These are:

1. in one dimension (1-D), the sine wave vibrational patterns of, for example, a violin string;

2. in two dimensions, upon a flat circular disc, vibrational patterns of a drumskin, made up of angular sine waves and radial ripples, which mathematically are called Bessel functions (Lacalli, 1981; Harrison and von Aderkas, 2004; see Fig. 6 below);

3. in three dimensions, upon a hemispherical shell, the vibrations of a hollow hemispherical bell (spherical harmonics, Y_l^m). Most scientists have met these patterns as angular parts of the hydrogen atom wave functions, with designations such as s, p, d, f corresponding to l = 0, 1, 2, 3. Table 1 lists the first few spherical surface harmonics relevant to plant patterns.

Fig. 6.

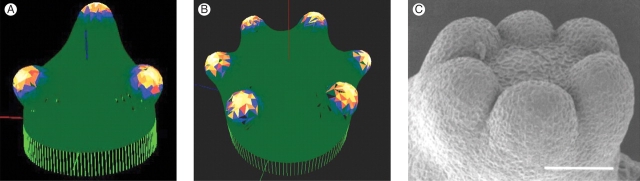
Higher-number branching, whorls. Again starting from tip growth, shorter pattern wavelength breaks symmetry into higher-number branching events, of three (A) to six (B) structures. The six lobes in B are not the steady-state chemical pattern for the initial hemisphere, but have been stabilized by surface growth. Such simultaneous whorl-forming events are common in plant development, such as flowers and conifer cotyledon formation (C, Larix leptoeuropaea, from Harrison and von Aderkas, 2004). Very high-number whorls, such as in Acetabularia (up to 35 structures), can form simultaneously, but may require prior formation of an annular pattern (Harrison et al., 1981, 1988; Harrison, 1992).

Table 1.

Harmonic wave patterns on a hemispherical shell

l	l(l + 1)	Analogous atomic orbital	Spherical surface harmonic, Ylm	Plant tip pattern
1	2	pz	Y10 or z	Dome-shaped tip
2	6	dxz,yz	Y2±1 or xz,yz *	Monocot embryo
3	12	fz3	Y30 or z3	Annulus (cup-shaped)
“	“	fxyz,z(x2−y2)	Y3±2 or xyz,z(x2−y2)	Dichotomous branches

* ‘±’ indicates a sum of the modes.

In all dimensionalities, any one pattern fits only a certain range of system sizes, and more complex patterns become optimal for larger size ranges. On the hemisphere, the change in pattern complexity with increasing l as listed in Table 1 comprises changes in shape more complex than the simple changes from half a wave to one wave to 1½ waves, etc., in 1-D systems. In place of the optimal wavelength λ, surface harmonics have an optimal hemisphere radius r related to λ by

3

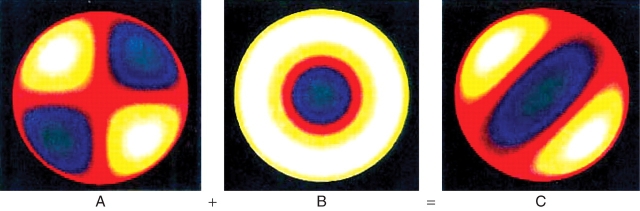
where λ is calculated from the reaction and diffusion parameters (Harrison, 1993; λ increases with increasing diffusivities and decreasing reaction rate constants). This implies that the same size of hemisphere is optimal for both dichotomous branching and annular patterns, so that both should start to grow equally together. Figure 2 shows that equal development of both patterns gives in fact a good dichotomous branching pattern.

Fig. 2.

The surface spherical harmonics Y₃² (A), Y₃⁰ (B) and their sum (C), corresponding to tip flattening (B) and dichotomous branching (A, C). Concentration is shown as a colour-map, with white/yellow high and green/blue low.

λ, or optimal r, depends on parameter values, particularly rate constants and diffusivities. Parameters common to all computations were a = 0·01, bB = 1·5, c = 1·8, d = 0·07, as in earlier work (Harrison and Kolář, 1988; Holloway and Harrison, 1999; Harrison et al., 2001). Parameters for specific results are given in Tables 2–5. The ratio D_Y/D_X was kept at 20, but the absolute values of the D's were varied to change the wavelength (harmonics) in particular computations. This does not have a mechanistic implication in regard to rates of diffusion. An alternative, and equivalent, procedure would be to keep the D's constant and vary the values of the chemical rate parameters. Parameter values were chosen to give the correct patterning behaviour according to the parameter space for Turing models devised by Lacalli (Lacalli and Harrison, 1979; Harrison, 1993). They can represent a fairly wide range of values in actual spatial and temporal units in various examples. As the simplest correlation, consider the rate constant d, which is the exponential decay constant of the substance X by itself. Its reciprocal is the ‘lifetime’ (i.e. time to decay to 1/e of initial X concentration). For d = 0·07, 1/d = 14. For a protein, 14 min would be a reasonable decay time, and if this was its value then our d would be directly in min^–1. However, within the wide range of biological diffusivities and pattern formation times, much faster or slower decay times could give the observed morphogenetic sequences. For the diffusion calculations, boundary conditions were no-flux, except for that in Fig. 7A, which was Dirichlet (fixed value).

Table 2.

Parameters for Fig. 4*

Figure	4A	4C	4E
DX	0·025	0·012	0·008
A gradient: max.–min.	Y10 : 6–1	Y10 : 16–1	as in 4C
Shown at time	3650	100	as in 4C

* C_g = 0·0125; X_th = 0·035; initial radius = 1; Δt = 0·1.

Table 5.

Parameters for Fig. 7*

Figure	7A	7B, C	7D	7E	7F	7G
DX	0·0018	0·0035	as in 7B	0·0007†	as in 7E‡	0·0005
Cg	0·001	as in 7A	as in 7A	as in 7A	as in 7A	0·01
Xth (changing at time)	N/A	0·08	0·08 (1000), 0·04	0·0 (1000), 0·15 (1050), 0·05 (1400), 0·15	0·0 (650), 0·15 (700), 0·05 (1050), 0·15 (1200), 0·05 (1250), 0·12	N/A
A gradient : max.–min.	uniform : 12	–(Y30 + Y32) : 13·9–1·2	as in 7B	as in 7B	as in 7B	(Y30 + Y32) : 41·1–7·2
Shown at time	1150	0, 1500	2050	2500	2050	4000

* Δt = 0·05, initial radius = 0·25.

^† Wavelength decreased continuously, with a halving time of 500 time units, between t = 1000 and t = 1500.

^‡ Wavelength decrease as above, but between t = 500 and t = 1750.

Fig. 7.

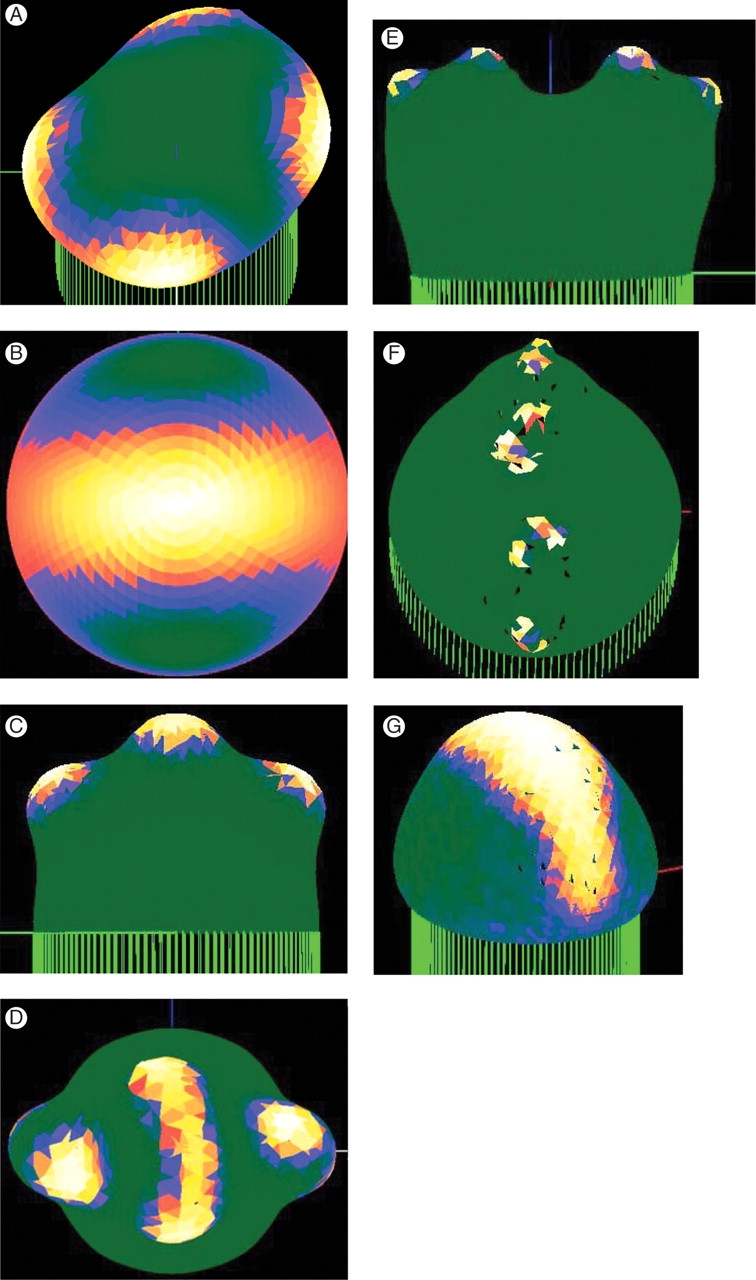
Successive co-planar dichotomous branching, key to understanding Micrasterias morphogenesis (and planation in the telome theory). (A) A pattern-forming mechanism with at least one wavelength between structures will tend to make new structures, once growth has made room for them, at right-angles, or as far away as possible, from the original structures (hemisphere initial shape). In most Micrasterias species, this only occurs in the polar lobe (Fig. 1). A persistent gradient in one of the precursors (reactant A) of the growth catalyst is effective at maintaining a branching plane, even starting from an initially hemispherical shape. (B) The simplest hemispherical pattern for defining a plane (equal mix of the spherical harmonics Y₃⁰ and Y₃², top view). (C) This prepattern can constrain primary branching to the plane (side view). (D) Secondary branching tends to be out-of-plane on the pole, but in-plane in the wings. The circular symmetry at the pole in the prepattern (B) does not constrain secondary branching direction, while the low concentration at low latitudes on the hemisphere gives the upthrust of the wings [away from the equator; see also (C) and Fig. 1A, B]. These distinctive features of Micrasterias morphology may result from the pattern of a precursor to growth. (E) For wing lobes, the prepattern is quite successful at constraining secondary branches to the same plane as the first branching. (F) With tertiary branching, lobes begin to drift from the plane. In Micrasterias, out-of-plane branches in the wings are generally observed at the terminal fourth or fifth branching (Fig. 1G). (G) Preliminary result on controlling growth without the catalyst threshold. Here, growth is proportional to the Y species in eqns (2A) and (2B), and patterning dynamics automatically cease at high precursor (A) levels. That is, switching off is not imposed in the computer code, it is a feature of the chemistry. Work is ongoing to understand the additional kinetics necessary to control complex 3-D growth (as in Figs  4–7F) with this purely chemical switching.

Table 3.

Parameters for Fig. 5

Figure	5A, B	5C, D
DX	0·0185	0·0007
Cg	0·0125	0·001
Xth (changing at time)	0·035	0 (1000), 0·15 (1100), 0·075
Initial radius	1	0·25
Δt	0·1	0·05
A gradient: max.–min.	Y10 : 6–1	– (Y30 + Y32) : 13·9–1·2 (shown in Fig. 7B)
Shown at time	250, 1000	1100, 2500

Table 4.

Parameters for Fig. 6*

Figure	6A	6B
DX	0·012	0·005
A gradient: max.–min.	Y10 : 6–1	as in 6A
Shown at time	2500	as in 6A

* C_g = 0·0125; X_th = 0·035; initial radius = 1; Δt = 0·1.

Finite element solution of rate equations

All computations start on a hemispherical or hemi-ellipsoidal shape, represented as a mesh of triangles (Fig. 3). In the initial mesh, all vertices (nodes) have a coordination number of 6 (i.e. are connected to six other nodes), except for the equatorial nodes, which have coordination number 3 or 4. The computations presented here were initialized with 1141 nodes. Numerical values of the concentrations in eqns (2a) and (2b) are defined at the nodes. The rates of change due to the reaction terms in eqns (2a) and (2b) were averaged over the three nodes of any triangle and multiplied by the area of the triangle. The diffusion terms in eqns (2a) and (2b) were approximated assuming a constant concentration gradient down the triangle from outside edge to central node, again taking into account triangle area. Both reaction and diffusion were summed over a finite element defined by all the triangles surrounding any given node. The eqn (2a) and (2b) PDEs were thus converted into a system of ordinary differential equations that were solved by a Runge–Kutta method, following the method of Ascher et al. (1997).

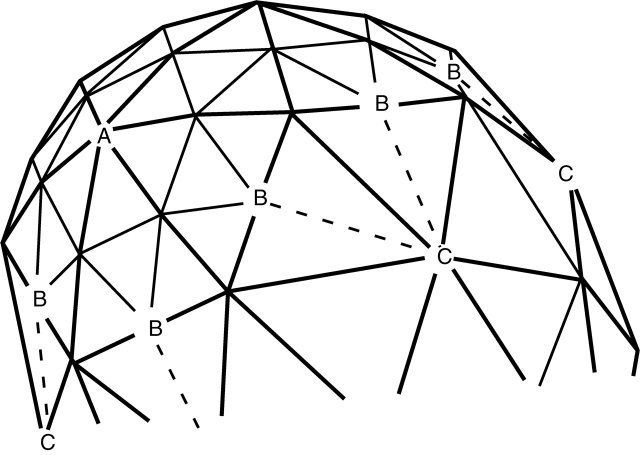
Fig. 3.

Computational representation of the surface, by finite elements. The initial shape (hemispherical or hemi-ellipsoidal) is represented by a triangular mesh. Reaction and diffusion are computed in elements defined by all the triangles surrounding each vertex, or node. Growth occurs by movement of nodes normal to the surface, according to the concentration of the growth catalyst (X) on the node. When any original triangle (heavy lines) has grown such that a side is twice its original length, a new triangle (light lines) is inserted inside it, in order to maintain accuracy. On boundaries between regions with new triangles (fast growth) and old triangles (slow growth), one-way connections (dashed lines B → C) are made, so that a node never has more than six neighbours.

Converting chemical pattern into shape change

Chemical pattern on the surface is converted into shape by moving nodes according to the concentration of X at each (ith) node. Area in each finite element increases by c_gX_iΔt, with growth constant c_g and time step Δt. The central node of the element is moved normal to the surface (outwardly, because of internal turgor pressure), until the prescribed area increase is met. The normal direction is found by averaging the normals of all the triangles in an element. The magnitude of nodal movement is found by approximating area increase as a quadratic function of nodal movement, making three test movements to determine the quadratic coefficients, and finally solving the distance for the specified area increase. An upper limit is set on this distance, to control movement instabilities. For growth-patterning stability, this area increase occurs once for every ten solution steps of the reaction-diffusion equations. To simulate as closely as possible the result of simultaneous growth of the whole surface, nodes are visited in random order to compute their movement. As growth occurs, and the surface changes shape, our surface representation by finite elements is superior, for solving the reaction-diffusion equations, to finite difference schemes, which depend on internode distances.

This method works well for shape change on convex regions of the surface, but can be less accurate in concavities. It is likely that bending stresses, surface shrinkage and sideways (tangential) surface displacement need to be considered in fully concave regions (both principal curvatures negative). For the 3-D work reported here, the algorithm copes with saddle points and adjacent regions where one of the principal curvatures is negative (concave) and the other positive (convex), giving a positive sum that allows growth stress to be relieved by outward movement. In our earlier 2-D work (Holloway and Harrison, 1999), the single negative curvature in a cleft could be accommodated only by arresting all growth and movement at such points.

Mesh refinement for a growing surface

In order to maintain an accurate representation of the shape, and to accurately solve the model (eqns 2a and 2b), new mesh must be incorporated in regions of high growth. Our choice of a triangular mesh allows us to insert new triangles into old ones (following Kaandorp, 1994). Once an original triangle has grown such that one of its sides is twice its original length, a new triangle is inserted, with vertices on the midpoints of the old triangle (Fig. 3, old triangles in heavy lines, new edges in light lines). This procedure maintains the original coordination number 6, except on boundaries between fast- and slow-growing regions. In order to maintain diffusion across these boundaries and to keep the coordination number close to 6 (for mesh stability), we define one-way junctions (B → C in Fig. 3), such that the new node B has the old node C as a neighbour, but not vice versa. [For another approach to this ‘non-conforming mesh’ problem, see Rivara and Inostroza (1995).] The resulting growing and proliferating mesh gives stable growth for up ten times expansion of the original surface area.

Software and computing facilities

The complete software package for combining reaction-diffusion and growth computations consists of 15 linked C programs (each calculating, for example, growth, refinement, triangulation, surface initialization and reaction-diffusion), about 20 000 lines in total. Computations have been run on IBM (AIX), HP (UX) and Linux workstations, and on the Linux cluster at the UBC Institute of Applied Math. Output is visualized with C/C++ programs, which call OpenGL graphics libraries. We have developed a Windows version of this software, which is available for general use (http://commons.bcit.ca/math/faculty/david_holloway.html).

RESULTS

With the model, it has been possible to simulate a number of the morphogenetic sequences observed in development. Starting from the conditions needed to maintain tip extension, we proceed to single symmetry-breaking events, and the control of multiple symmetry breaking for more complex examples of body architecture. This work involved much ‘computer experimentation’, in which parameter values were chosen to achieve the desired patterns. In particular, the wavelengths of patterns were selected by the value of D_x, and complex repeated branching events required changes in the value of X_th, occasionally several times in the course of a computation (Table 5, see Fig. 7F). This is in the spirit of our earlier 2-D work on Micrasterias (Holloway and Harrison, 1999) and may point towards changing surface patterns being influenced by timing events within the cell. These should be experimentally discoverable.

Tip growth, and circularly symmetric transitions

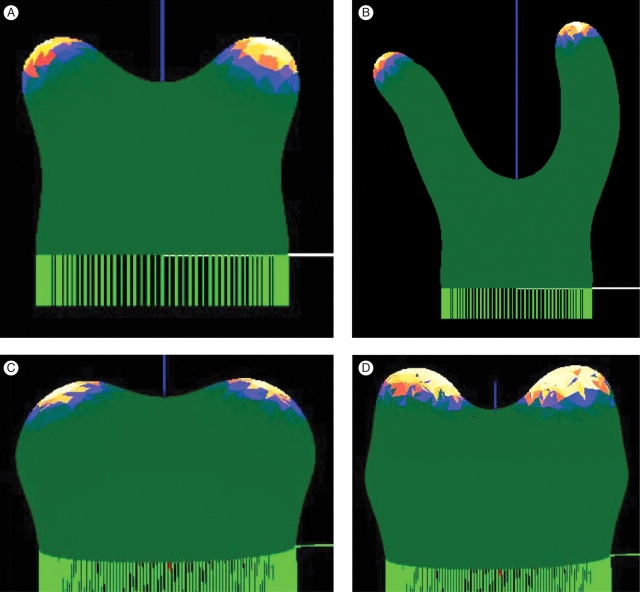
Tip growth is one of the fundamental modes of morphogenesis in plants. Once an initial direction has been selected, tips require a specific pattern of growth rates to extend. For a hemisphere to be the steady-state shape of an advancing growing tip, Green and King (1966) showed mathematically that morphological growth rate must vary as the cosine of the co-latitude. (This function is the Y₁⁰ spherical harmonic, Table 1.) For a chemical patterning mechanism capable of breaking symmetry, such as ours, there must be a mechanism to limit the extent of the region of patterned growth rates, despite surface being extended behind the growing tip. That is, the ‘stalk’ must become inactive to chemical patterning. In our model, this is achieved through the X_th value; for the correct range of X_th, patterning is cut off at the ‘equator’ of the active patterning region, such that this boundary moves with the growing tip, and maintains the cosine growth rate for steady-state tip extension. Figure 4A shows a computation in which tip extension has proceeded for over a ten-fold increase in height (computational parameters for Fig. 4 are given in Table 2). The tip direction changes slightly over such long computations. This is observed for a range of mesh coarsenesses (271–2611 initial nodes) and different random orders of node movement. As there are no external tropisms in the model, this tip wandering is not unexpected, and is seen, for example, with many runners and vines. Figure 4B looks down on a tip after extensive growth, showing the irregularity of the mesh after many new triangles have been added (compare with the regular mesh on the original hemisphere below the tip). The local irregularity does not appear to affect overall shape; this is robust over a wide variety of mesh coarsenesses and random order of node movements.

Fig. 4.

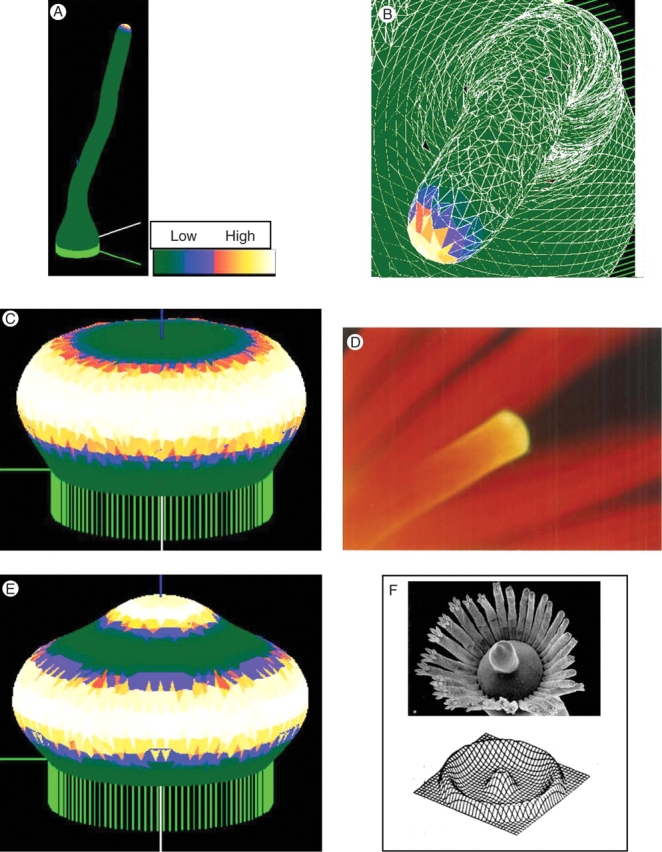
Tip growth. (A) Extended tip growth, over ten times the starting height. Concentration of the X growth catalyst is shown by a colour-map, with white/yellow high and green low. (B) Detail looking down on a tip, after extensive growth. The computational mesh is shown in white. The wanderings in tip direction do not depend on the coarseness of the mesh or the random order of node movement, but arise because there are no external tropisms in the model. (C) Changing the fit of the pattern to the tip size, by increasing reaction rates in this case, induces a transition to an annular pattern, giving tip flattening. (D) Flattening is a fundamental process in many developmental sequences, for instance in embryonic development, and preceding hair whorl formation in the Dasyclad algae Acetabularia (shown). Calcium chlorotetracycline fluorescence, yellow against a background of red chlorophyll autofluorescence, from a growing tip at the onset of vegetative whorl formation. Photograph taken by B. Lakowski. (E) Continued growth can lead to a new central pattern maximum, required for re-initiation of extending tip growth in Acetabularia (F) (from Berger and Kaever, 1992, with permission). Such a sequence of patterns, but in a uniformly growing system, was first demonstrated by G. Zeiss, in Harrison et al. (1981); also (F).

In many cases of morphogenesis, tips flatten prior to a breaking of symmetry (e.g. Figs 4D; see also Fig. 6C below). This transition can be described as a change in the fit of pattern to the tip size, i.e. as a transition from the Y₁⁰ spherical harmonic to the annular Y₃⁰ spherical harmonic. Change in fit can occur either by increasing the tip size, which corresponds to lowering X_th in the model to retard boundary advance, or by decreasing the pattern wavelength, by decreasing diffusivity or increasing reaction rates. Figure 4C shows a flattened tip resulting from the latter approach. In a case such as Acetabularia morphogenesis (Fig. 4D), tip flattening (which precedes the initiation of a whorl of hairs) must be followed by re-initiation of tip growth, in order for main stalk development to proceed (Fig. 4F). This again results from surface expansion or wavelength decrease to fit a higher harmonic on to the tip. Figure 4E shows this, having lower diffusivity than Fig. 4C. This response, for a uniformly growing surface, was demonstrated by G. Zeiss (Fig. 4F; Harrison et al., 1981).

Dichotomous branching

On hemispherical tips, the first possible pattern that breaks circular symmetry is the Y₂¹ harmonic, which corresponds to off-centre tip growth, as in the embryogenesis of monocots. The long-term architecture, however, is not greatly different from centred tip growth. Dichotomous branching has a greater effect on architecture, and not only underlies the embryogenesis of dicots and much plant development, but is the central event in Micrasterias development. In terms of hemispherical patterns, branched growth corresponds to a mix of the annular Y₃⁰ and ‘quartered’ Y₃² patterns (Fig. 2). Transition from tip growth to dichotomous branching can be achieved, as with tip flattening, by tip expansion or reduction of wavelength. Figure 5A has identical conditions to Fig. 4A, except for reduced diffusivity (reduced wavelength). In earlier work, we reported that 3-D computations allowed us to remove the ad hoc ‘locking’ of node positions needed in two dimensions to maintain clefts (Harrison et al., 2001). In that work, however, growth was arbitrarily set to zero in morphogenetically ‘dead’ regions. In the present computations, we no longer do this, but rather allow X-dependent growth over the whole surface. Geometry, in three dimensions, is still sufficient to constrain cleft position, and allow lobe outgrowth.

Fig. 5.

Simple dichotomous branching. (A) Starting from tip growth, shorter wavelength breaks symmetry to give a dichotomous branch. (B) The new growing regions undergo independent tip extension. The 3-D geometry of the cleft, with slow growth at right-angles to the branching plane, is sufficient to maintain the branching morphology. (C) With the catalyst threshold mechanism introduced in Holloway and Harrison (1999), patterning ceased below a threshold value, leaving only decay of the catalyst. This created a ‘drain’ for catalyst in slow-growing regions, which contributed to acute branching angles in two dimensions. In three-dimensions, however, the effect on branching angle is much more pronounced, such that initial broad branching angles (C, about 80°) can be turned nearly parallel (D, about 20°). Modelling acute branching is challenging in two dimensions, but the 3-D results suggest geometry may be helping plants consistently form acute branches.

After branching, the new tips can undergo extensive tip growth (Fig. 5B). In two dimensions, we found the –dX decay in morphogenetically ‘dead’ regions to be important for achieving acute branching angles (Holloway and Harrison, 1999). In three dimensions, this effect can be very strong, and indeed reduce angles that initially are large (Fig. 5C, D). This difference is probably due to the –dX ‘drain’, which tends to force peaks together, being proportional to surface area in three dimensions, rather than linear distance. Such a decrease in branching angle is observed, for example, in development of Acetabularia whorls (Fig. 4F), in which initially wide angles between hairs decrease at early stages of hair extension.

Higher-number branching, whorls

A further decrease of wavelength from that which gives dichotomous branching might be expected to give larger numbers of branches. Figure 6A shows a branching to three outgrowing lobes, generated by a decrease in diffusivities from Fig. 5A values. Upon a hemisphere, growing or not, but of unchanging shape, it is well known to theorists (but rarely reported, being a negative conclusion) that when the number of branches exceeds three or four, computations usually give them randomly distributed over the whole hemisphere, not organized in a whorl. Hence, we have (Harrison et al., 1981, 1988; Harrison, 1992) hypothesized for large-number whorl formation a two-stage hierarchical mechanism, with the first mechanism defining an annular pattern and the second branching it into multiple lobes. Figure 6B, however, shows a six-lobe whorl formed by the single-stage mechanism of the present study. This pattern is, however, dependent on growth rate and shape change from the initial hemisphere. Slower growth rate with the same chemical rate parameters and diffusivities gave a dichotomous pattern. Most probably, formation of incipient branches has led to tip flattening without the need for an annulus-forming mechanism, and the six-lobe whorl is patterning on a shape more like a flat disc than a hemisphere. Experimentally, Fig. 6C shows the apex of a somatic embryo of a hybrid larch with six cotyledons forming (Harrison and von Aderkas, 2004). Analysis of data for embryos with from one to eight cotyledons in this species showed that the patterns were a spatially quantitative fit to a particular set of 2-D harmonics (drumskin vibration patterns, radial Bessel functions with angular sine wave functions). Many plants exhibit whorls of from three to eight structures (e.g. flowers of monocots and dicots). We have yet to undertake detailed studies of just which of many drumskin patterns should be fastest forming on a disc, and what diverse patterning behaviours may be possible in a system changing shape at various rates from a hemisphere towards a disc. For very high-number whorls (vegetative whorls of Acetabularia can have up to 35 hairs), our hypothesis of two-stage hierarchical patterning stands.

The tip growth to branch transition is more complex in three than in two dimensions. A 2-D branch could represent the cross-section of three possibilities in three dimensions: an annulus (Fig. 4C); a dichotomous branch (Fig. 5); or a higher-branching whorl, such as that in Fig. 6B. The present computations begin to show how fit of pattern to tip size controls these possibilities in 3-D development.

Successive dichotomous branching and control of branching plane

After mitosis, a Micrasterias daughter cell generates the form of its missing half by successive dichotomous branchings from an initial ‘bubble’ of cell surface (Fig. 1A). To form this flat structure, not only must successive branchings be all in the same plane, but that plane must somehow be specified as the plane of the existing mature semicell. The question of how this specification works was raised more than half a century ago by Waris (1950), who speculated upon ‘cytoplasmic inheritance’; Lacalli (1976) favoured the concept of a ‘morphogenetic template’ in the cell surface, somehow related to the slightly non-circular shape of the isthmus between old and new semicells. The problem remains unsolved.

A pattern related to Y₃ spherical harmonics can specify a plane of bilateral symmetry either as containing the line between two concentration maxima (Fig. 2C, white) or by the blue band perpendicular to this. Our computed patterns for a first dichotomous branch from a hemispherical starting shape (Fig. 5) give patterns very similar to that in Fig. 2C. It is evident that a second branching from the two white-and-yellow regions will almost always be at right-angles to the first branching, because these regions are extended in that direction. Our computations confirm this decussate pattern for successive branchings (Fig. 7A; Harrison et al., 2001, Fig. 8e–g). An additional feature to the simple harmonic wave-generating mechanism is needed to keep successive branchings in the same plane. We have studied two possibilities for this specification of the morphogenetic template: the initial shape of the growing surface, and pre-patterning of the chemical inputs A or B in the Brusselator mechanism (eqns 1, 2). A number of computations starting from hemi-ellipsoidal instead of hemispherical shape showed that the direction of a second branching is quite insensitive to shape; it was still at right-angles to the first branching for axial ratios up to 6 : 1.

Within the model, we can test the ability of chemical gradients to constrain the branching plane. For general applicability, as envisaged in the telome theory for multicellular plants, such work is in the spirit of the review of Beerling and Fleming (2007), who discuss ‘planation’ in relation to auxin fluxes and PIN gene expression patterns, i.e. they envisage control of the 3-D geometry of branching by chemistry. A natural ‘planar’ gradient for the hemisphere is the negative of the mix of Y₃ spherical harmonics shown in Fig. 2. This pattern is used for the precursor A (Fig. 7B). With this gradient, we have been able to constrain successive branches to the same plane, with a hemispherical initial shape. Figure 7C shows that the primary lobes are directed upwards, as in Micrasterias, due to the pattern in the A gradient. Secondary branches are in the original branching plane in the wing lobes, but out-of-plane in the polar lobe (Fig. 7D). The different planarities of the wing and polar lobes stem from the more circularly symmetric A pattern at the pole, as compared with the wings, a natural feature of the spherical harmonic. This may underlie the observed differences in wing and pole branching planes in most species of Micrasterias. The A gradient is quite successful in generating in-plane secondary branches (Fig. 7E, modelling ‘wing’ lobe). To generate repeated branches, two features were added to the model: (1) to maintain clefts while new peaks are generated nearby, an irreversible ‘death’ was imposed, such that once a node fell below X_th, it could not be rescued by movement of high X into that region (a region which loses pattern-forming ability is no longer competent subsequently to activate it); and (2) decrease of wavelength (through continuous decrease of D_X, D_Y) to decrease the size of the lobes, a feature of Micrasterias important for avoiding lobe overlap (Lacalli and Harrison, 1987, showed that M. rotata wavelength halves over three branching events; here, with the surface growth rate used, we halved wavelength over one branching event). It has been possible to generate up to tertiary branches in the model (Fig. 7F). For the tertiary branches, the upper wing lobes branch in advance of the lower wing lobes, as seen in the development of M. rotata (Lacalli and Harrison, 1987); this is due to the greater A concentration closer to the pole (Fig. 7B). The last branches tend to adhere to the plane of the gradient less than earlier branches. Similarly, in many species of Micrasterias, the small, final branches are out-of-plane with the rest of the wing lobe (Fig. 1G). In the model, this arises as local growth is catalyzed by fairly circular X peaks and lobe tips are created which retain little of the original A gradient asymmetry. In nature, maintaining branching plane for four or more branchings may depend on active patterning of the precursor gradient, such that the gradient asymmetry is maintained on the shape as a whole, rather than being lost through local isotropic growth. Such a double pattern-forming mechanism would be akin to the hierarchical mechanism previously proposed for high-number whorl formation in Acetabularia (Harrison et al., 1981, 1988; Harrison, 1992).

In separate work, with R. J. Adams, we have begun to develop a mechanism (in one dimension), which could not only be applied to such hierarchical pattern formation, but replaces the arbitrary assumption of an X_th by a feedback model between two Brusselators (‘feedback loop III’ in Harrison et al., 1988, 2001; Harrison, 1992) that explains the chemical–dynamic origin of the threshold effect. In the Brusselator, with growth depending on the concentration of Y, boundaries between fast patterned growth and slow uniform growth can be dictated by the Turing (1952) conditions inherent in the mechanism dynamics. As a preliminary step towards seeing how this might work in 3-D shape change, we have run single-mechanism (eqns 1A–D) computations in which growth is proportional to Y (Fig. 7G). These computations have a precursor A gradient as in Fig. 2C, but dynamically maintain that pattern with growth. Such a mechanism could serve as the start of a hierarchical mechanism for maintaining branching plane through four or five branchings. Morphologically, such shapes are seen in non-branching desmids, such as Cosmarium, which may have only the initial half of the double mechanism that highly branching Micrasterias species might require.

DISCUSSION

The work presented in this paper has two main features: (1) the representation of a growing plant surface in computations by an expanding mesh that has no artefacts constraining changes of shape and symmetry; and (2) the study of how much in plant development is explicable by one type of patterning-forming mechanism, Turing-type reaction-diffusion, acting within the represented surface and expressing pattern through catalysis of area increase. These two features are not linked one-to-one. The setting up of the mesh in a finite-element manner, with means for displacement of the elements in response to any putative pattern-forming mechanism, and means for refinement of the mesh as it grows, is a major project in itself. Many features of the responses of the mesh could probably be illustrated and studied with developmental mechanisms other than reaction-diffusion (which we are nevertheless advocating as having substantial promise to be what is actually going on in plant development).

The study has focused on the dynamic constraints necessary for pattern selection in plants. Experimental verification of the results would require not only an identification of patterning molecules, but estimates of concentration alongside measurements of cell surface expansion, in order to achieve a quantitative description of morphogenetic sequences, against which our estimates of relative rates could be checked and calibrated.

Phenomenologically, we are trying to address the problems of how a tip or shoot apex contrives to limit its own size while it contributes to the formation of a much larger structure, and how two or more new branches each manage to acquire within their own apices all the developmental apparatus of the former single apex. This may, as indicated particularly in relation to Fig. 6, require consideration of sequential pattern-forming steps interacting through feedback loops. We are pursuing this in 1-D work, but it is beyond the current scope of the 3-D studies described here. Patterns produced by a single reaction-diffusion mechanism have proved capable of producing the developmental phenomena illustrated in Figs 4–7.

What are we implying by concentrating our efforts on manipulation of a surface? If this represents membrane and wall of a single cell, it might be expected to take its shape changes from action of a mobile scaffolding within the cytoskeleton. The example of Micrasterias, however, is one for which there is substantial evidence to localize pattern-forming and shape-changing activity at the cell surface (Kiermayer and Meindl, 1989). A surface, as implicitly defined by our representation of it in the computer, is any region that is very much more extensive in area than it is thick, and unconstrained for movement normal to its own plane in one direction (outward). For multicellular plants, the tunica (commonly a single layer of cells) can be regarded as a surface. (And, indeed, for single cells, a cortical layer of cytoskeleton could be incorporated into our concept of a surface, provided only that it is thin enough.)

Just as the surface, represented by the triangulated mesh in our computations, may have many different structural identities in diverse living systems, so the molecules represented by A, B, X and Y in our computations may have diverse identities. Calcium ions have been found in concentration-patterned attachment to plasma membranes in Acetabularia (Fig. 4D) and Micrasterias (Meindl, 1982). Binding of calcium by membrane-bound proteins has been suggested in both cases. Beerling and Fleming's (2007) review of the telome theory invokes patterned auxin fluxes and genes such as PIN, active on shoot apical meristems. We advocate that people working upon all such molecules should think also of rates of processes involving them as an equally ultimate reality in explaining development, and we offer our computational results in that spirit.