Effects of ignoring baseline on modeling transitions from intact cognition to dementia

Abstract

This paper evaluates the effect of ignoring baseline when modeling transitions from intact cognition to dementia with mild cognitive impairment (MCI) and global impairment (GI) as intervening cognitive states. Transitions among states are modeled by a discrete-time Markov chain having three transient (intact cognition, MCI, and GI) and two competing absorbing states (death and dementia). Transition probabilities depend on two covariates, age and the presence/absence of an apolipoprotein E-ε4 allele, through a multinomial logistic model with shared random effects. Results are illustrated with an application to the Nun Study, a cohort of 678 participants 75+ years of age at baseline and followed longitudinally with up to ten cognitive assessments per nun.

1. Introduction

In most longitudinal studies on progression of healthy individuals to chronic diseases, such as cancer, AIDS and dementia, the outcome of interest is a series of correlated binary or polytomous responses where these responses are observed at certain time points, sometimes several years apart. Generalized linear mixed models (GLMM) are suggested to account for the dependency among repeated follow-up waves within the same subjects, where unit-specific effects are realizations of some random effects (Stiratelli et al., 1984; Gibbons and Hedeker, 1994; Crouchley, 1995; Skrondal and Rabe-Hesketh, 2004; Salazar et al.,2007).

Salazar (2004; 2007) introduced a multi-state Markov model for longitudinal data with categorical responses. The model maintains the GLMM structure by accounting for conditional effects of covariates given the values of a single shared random/latent effect. In addition, two particular features are presented in his model. First, the dependency among observations on the same subject is addressed by assuming a first-order Markovian structure, which helps to facilitate the expression of the joint distribution of the response vector. Second, the parameterization of the transition probabilities using multinomial logistic regression provides a closed-form expression in the likelihood construction. The model provides a suitable approach to problems of identifying the risk factors associated with the progression of healthy individuals to a chronic disease with death treated as a competing event.

However, Salazar’s model approximates the joint distribution of the response variable using a conditional distribution given the baseline outcome of the response variable. Such an approach could possibly produce a so-called ‘baseline confounding’ problem (Crouchley and Davies, 1999; Ten Have et al., 2002), which might result in biased or inconsistent estimation. The model application in the Nun Study on progression of dementia indicates that among 678 subjects in the cohort, 77 are demented at baseline. These subjects (more than 10 percent) were removed from the analysis since they would contribute nothing to the likelihood when ignoring baseline. It is interesting to see how the model likelihood as well as maximum likelihood estimates (MLEs) will differ once we incorporate baseline information into the model construction.

This paper will focus on addressing this limitation by accommodating the baseline confounding in the Markov model using shared random effects approaches. In the next two sections, the model likelihood construction is discussed in detail. In sections 4 and 5, simulation studies and an application to the Nun Study data discussed in this context by Tyas et al. (2007) are presented. Comparisons are made between the two models with respect to maximum likelihood estimation. Section 6 discusses how this model structure can be modified to accommodate higher orders of the chain and the possibility of testing these chain orders using conventional likelihood ratio tests.

2. Markov model with shared random effects

A generalized linear mixed model (GLMM) for a longitudinal analysis is defined as follows, let i denote a particular subject under study and n_i the number of repeated observations for subject i. Suppose the link function for the response is η. The model can be written as

$$\eta (E(y_{ik}\mid {\mathit{X}}_{ik},{\mathit{\gamma }}_i))={\mathit{X}}_{ik}^{\prime }\mathit{\beta }+{\mathit{W}}_{ik}^{\prime }{\mathit{\gamma }}_i$$

where k = 1,2,…,n_i. Here β is a p dimensional vector of unknown parameters (fixed effects) associated with the corresponding observed covariate vector X_ik. γ_i. is a vector of unobserved random effects associated with subject i. Considering that W_ik is typically contained in the elements of covariates X_ik (Zeger and Karim, 1991; Skrondal and Rabe-Hesketh, 2004), we assume the expectation of the response variable depends only on X_ik and the random vector γ_i.

In contrast with the general GLMM, the Markov model introduced by Salazar (2004; 2007) demonstrates two favourable features in modeling longitudinal categorical responses as a multi-state system where series of categorical outcomes are expressed in terms of states, and the onset and progression of these outcomes as transitions between the states.

First, the model relies on a ‘transitional modeling’ (Agresti, 2002) strategy by introducing a multi-state discrete-time Markov chain, which facilitates the expression of the joint distribution function. The natural development of chronic diseases can often be expressed in terms of distinct health stages and the Markov chain is a simple yet powerful tool in describing the progression of healthy individuals through these stages. Assume the Markov property that the conditional distribution P(y_ik|y_i0…y_ik−1) is identical to the conditional distribution of P(y_ik|y_ik−1). The conditional joint distribution function for a particular subject i, given the baseline observation y_i0, can then be factorized as follows

$$f(y_{i1},\dots ,y_{i{n}_i}\mid y_{i0})=f(y_{i1}\mid y_{i0})f(y_{i2}\mid y_{i1})\dots f(y_{i{n}_i}\mid y_{i{n}_i-1})$$

Here each y_ik, k = 1,2,…, n_i, refers to the state that the i th subject is in at the k th observation. Each conditional probability f(y_ik|y_ik−1) therefore can be interpreted as a particular element inside the one-step transition probability matrix. More specifically, suppose y_ik−1 = s and y_ik = v. Then f(y_ik=v|y_ik−1 = s), denoted by P_sv (X, γ), is simply the probability of transition for subject i from state y_ik−1 = s at k −1 th visit to y_ik = v at k th visit, where s and v are elements of finite transition states within a particular multi-state system.

Second, by applying multinomial logit parameterization, the model provides a closed form in constructing the model likelihood function. For presentation purposes, we assume a finite stochastic system consisting of five transition states with three transient and two competing absorbing states. This corresponds to the five progression stages in the study of dementia (Tyas et al., 2007) and these are (1) intact cognition, (2) mild cognitive impairment (MCI), (3) global impairment (GI), (4) dementia and (5) death. The one-step transition probability matrix could then be presented as below

$$\left[\begin{array}{ccccc}{P}_{11}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{12}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{13}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{14}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{15}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })\\ P_{21}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{22}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{23}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{24}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{25}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })\\ P_{31}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{32}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{33}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{34}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })& P_{35}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]$$

Since ${\displaystyle \sum _{v=1}^5}{P}_{sv}(\mathit{X},\mathit{\gamma })=1$ for each row of s = 1,2,…,5, a nominal polytomous logistic model for P_sv can be constructed as

$$log\left(\frac{P_{sv}({\mathit{\theta }}_{sv}\mid \mathit{X},\mathit{\gamma })}{P_{s1}({\mathit{\theta }}_{s1}\mid \mathit{X},\mathit{\gamma })}\right)={\alpha }_v+{\mathit{X}}^{\prime }{\mathit{\beta }}_v+{\mathit{\xi }}_v(s)+{\mathit{W}}^{\prime }\mathit{\gamma }$$

where v = 2,3,4,5. Let Θ represents the set of all unknown parameters (α||β||ξ(s)), where α is the vector of intercepts; β is the vector of unknown fixed effects for covariates of interest; and ξ (s) is the set of unknown fixed effects for the prior state. The inclusion of ξ (s) serves two purposes in the model. First it helps to define the row characteristics of the transition matrix; the parameterization assumes that α||β does not depend on the prior state, so that α||β applies for each row, and the inclusion of ξ (s) therefore differentiates among rows. Second, the inclusion of the previous state somewhat absorbs the possible correlation among residual errors so as to guarantee the independence and constant variance of model residuals conditional on the fixed and random effects (Stiratelli et al., 1984).

Following Salazar (2004; 2007) each transition probability can be postulated in the form of

$$P_{sv}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })=\{\begin{array}{c}\frac{1}{1+{\displaystyle \sum _{h=2}^5}exp({\alpha }_h+{\mathit{X}}^{\prime }{\mathit{\beta }}_h+{\mathit{\xi }}_h(s)+{\mathit{W}}^{\prime }\mathit{\gamma })}\\ \frac{exp({\alpha }_v+{\mathit{X}}^{\prime }{\mathit{\beta }}_v+{\mathit{\xi }}_v(s)+{\mathit{W}}^{\prime }\mathit{\gamma })}{1+{\displaystyle \sum _{h=2}^5}exp({\alpha }_h+{\mathit{X}}^{\prime }{\mathit{\beta }}_h+{\mathit{\xi }}_h(s)+{\mathit{W}}^{\prime }\mathit{\gamma })}\end{array}$$

The first equation applies for v = 1, and the second for v = 2,···5.

3. Likelihood functions

The estimates produced in Salazar’s multi-state Markov model are based on a likelihood that conditions on the baseline response. The model further assumes that the distribution of the random effects γ is independent of both baseline outcome and covariates. Such an approach could possibly produce a so-called ‘baseline confounding’ problem (Crouchley and Davies, 1999; Ten Have et al., 2002), which might result in biased or inconsistent estimation. To see this, the complete likelihood function for the model is

$$L_c=\int \prod _i\prod _{t}f(y_{it}\mid y_{i0},{\mathit{X}}_i,\mathit{\gamma })dh(\mathit{\gamma }\mid y_{i0},{\mathit{X}}_i)$$

Here ${\displaystyle \prod _t}f(y_{it}\mid y_{i0},{\mathit{X}}_i,\mathit{\gamma })$ refers to the product of individual transition probabilities of ${\displaystyle \prod _{k=1}^{n_i}}{P}_{y_{ik-1,}{y}_{ik}}(\mathit{\Theta }\mid {\mathit{X}}_i,\mathit{\gamma })$. Under Salazar’s assumption, the following likelihood is used

$$L_s=\int \prod _i\prod _{t}f(y_{it}\mid y_{i0},{\mathit{X}}_i,\mathit{\gamma })dh(\mathit{\gamma })$$

Crouchley and Davies (1999) argue that if it is possible for the random effects to be independent from the model covariates, the independence of random effects and baseline outcome is difficult to justify. The latent variables which contribute to the random effects are likely to be at least partially responsible for the observed baseline states. This is especially the case for a cohort with heterogeneous baseline where the assumption about the independence between random effect and baseline outcome can not be taken for granted.

Considerable literature has focused on constructing extended likelihood functions to accommodate missing data that are non-ignorable, such as informative drop-out and death in particular (Rubin, 1976; Ten Have et al., 1998; Pulkstenis et al., 1998; Ten Have et al., 2000, Gao, 2004). Sharing of random effects has been a popular approach in this respect. The method incorporates into the likelihood construct both the follow-up response and drop-out response components by assuming that the two share the same random parameters and are conditionally independent given these random effects (Ten Have et al., 1998). In essence, the model likelihood is built up using a separability approach. Suppose γ is a vector of m dimensional unobserved random effects contributing to both the probability of follow-up and drop-out responses, and let γ have some prior distribution function h. The marginal joint distribution for the follow-up and drop-out can be expressed as

$$f^{″}({\mathit{y}}_{\mathit{i}},z_i)=\int f^{\prime }({\mathit{y}}_{\mathit{i}}\mid \mathit{\gamma })g(z_i\mid \mathit{\gamma })h(\mathit{\gamma })d\mathit{\gamma }$$

where f′ (y_i|γ) and g(z_i|γ) are the conditional distribution for follow-up and drop-out responses given γ. A similar approach is possible for the purpose of improving our model likelihood by accounting for the baseline information. We hypothesize that the shared random effects approach that has been used to account for the informative drop-out can be analogously applied in this situation where the drop-out function g(z_i|γ) is replaced with f (y_i0|γ), the baseline response given γ, assuming the two share the same random effects).

Ten Have et al. (2002) take this approach in modeling longitudinal binary functional limitation responses. Their model considers both baseline confounding and informative drop-out, in which case the model likelihood consists of three separate components: one for baseline, one for follow-up outcomes and one for time of drop-out. These three pieces are conditionally independent given random effects and their corresponding predictor variables. The key difference between Ten Have’s model and ours is that, on the one hand, the drop-out is of little concern in our case and by omitting the drop-out component it simplifies the model construction. On the other hand, our case involves multinomial responses and the parameterization using polytomous logit under a discrete-time Markov framework is more complicated than the simple Bernoulli approach for binary outcomes.

The inclusion of baseline outcome variable completes the joint distribution function, and the equation now becomes

$$\begin{array}{l}f(y_{i0},y_{i1},y_{i2},\dots ,y_{i{n}_i}\mid \mathit{\gamma })\\ =f(y_{i1},y_{i2},\dots ,y_{i{n}_i}\mid y_{i0},\mathit{\gamma })f(y_{i0}\mid \mathit{\gamma })\\ =f(y_{i1}\mid y_{i0},\mathit{\gamma })f(y_{i2}\mid y_{i1},\mathit{\gamma })\dots f(y_{i{n}_i}\mid y_{i{n}_i-1},\mathit{\gamma })f(y_{i0}\mid \mathit{\gamma })\end{array}$$

Using the previous example of the five-state transition system, let π_j = P(y_i1 = j) represent the probability that subject i is in some state j at the baseline. We propose to model the probability of the baseline state similarly by using multinomial logistic regression, which gives

$${\pi }_j({\mathit{\varphi }}_j\mid {\mathit{X}}_B,\mathit{\gamma })=\{\begin{array}{c}\frac{1}{1+{\displaystyle \sum _{h=2}^4}exp({\tau }_h+{\mathit{X}}_B{\mathit{\delta }}_h+W_B^{\prime }\mathit{\gamma })}\\ \frac{exp({\tau }_j+{\mathit{X}}_B{\mathit{\delta }}_j+W_B^{\prime }\mathit{\gamma })}{1+{\displaystyle \sum _{h=2}^4}exp({\tau }_h+{\mathit{X}}_B{\mathit{\delta }}_h+W_B^{\prime }\mathit{\gamma })}\end{array}$$

Again the first equation applies for j = 1, and the second for j = 2,···4. Here the vector ϕ_j ≡ (τ_j||δ_j) represents another set of unknown parameters determining the baseline probabilities. The likelihood function can now be written as

$$L(\mathit{\Theta },\mathit{\Phi }\mid \mathit{X})=\int \prod _i\prod _{k=1}^{n_i}{P}_{y_{ik-1,}{y}_{ik}}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma }){\pi }_{y_{i0}}(\mathit{\Phi }\mid {\mathit{X}}_B,\mathit{\gamma })h(\mathit{\gamma })d\mathit{\gamma }$$

y_i0,y_i1···y_ini. are known states, Θ is the parameter vector associated with the follow-up response component and Φ is the parameter vector associated with the baseline response component. For the purpose of presenting the marginal likelihood, we rewrite ${\displaystyle \prod _{k=1}^{n_i}}{P}_{y_{ik-1,}{y}_{ik}}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })$ in some closed form considering that y_ik−1 and y_ik can be any arbitrary states from 1 to 5. ${\displaystyle \prod _{k=1}^{n_i}}{P}_{y_{ik-1,}{y}_{ik}}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })={\displaystyle \prod _{k=1}^{n_i}}\times {\displaystyle \prod _{\begin{array}{l}s=1\dots 5,\\ v=1\dots 5\end{array}}}{(P_{sv}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma }))}^{{\delta }_{y_{ik-1},s}{\delta }_{y_{ik},v}}$, where δ_yik−1,s and δ_yik,_v are some indicator functions valued at 1 if y_ik−1 = s and y_ik = v and 0 otherwise.

Since the last two rows of the transition probability matrix contribute nothing to the likelihood, the range of s can be reduced to include only the transient states. The final likelihood function for under this 5-state system becomes

$$\int \prod _i\prod _{k=1}^{n_i}\prod _{\begin{array}{l}s=1\dots 3,\\ v=1\dots 5\end{array}}{(P_{sv}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma }))}^{{\delta }_{y_{ik-1},s}{\delta }_{y_{ik},v}}{\pi }_{y_{i0}}(\mathit{\Phi }\mid {\mathit{X}}_B,\mathit{\gamma })h(\mathit{\gamma })d\mathit{\gamma }$$

As an extension, note here that the vector γ is not necessarily random effects per se. It could also be some reparameterization of the random effects such that the model could allow different variance covariance structures of random effects for f_yik,1<=k=ni(y_i1,y_i2,…y_ini|γ, y_i0) and f(y_i0|γ) respectively.

Furthermore, the Cholesky decomposition of a positive definite variance covariance matrix can be used to account for the correlation among random effects. To be more specific, suppose Σ is a positive definite variance covariance matrix for the random effect vector γ. Then Σ can be rewritten in the form of Σ = U′U where U is some upper triangular matrix and the equation $\eta (E(y_i\mid {\mathit{X}}_i,{\mathit{\gamma }}_i))={\mathit{X}}_i^{\prime }\mathit{\beta }+{\mathit{W}}_i^{\prime }{\mathit{\gamma }}_i$ can be modified as $\eta (E({\mathit{y}}_i\mid {\mathit{X}}_i,{\mathit{\gamma }}_i))={\mathit{X}}_i^{\prime }\mathit{\beta }+{\mathit{W}}_i^{\prime }{\mathit{U}}^{\prime }{\mathit{\rho }}_i$. Notice that now the random effect vector γ has been reparameterized as U′ρ where ρ has the variance covariance matrix being an identity matrix I. For a random intercept-slope model, for example, each row of matrix W is composed of two elements, 1 and a covariate value changing within the subjects, age for instance. U is a 2 by 2 matrix in which two diagonal elements are σ₁, and σ₂, the square root of the variance for intercept and slope random effects. The upper off diagonal element is σ₁₂, the covariance between the two, and the lower off diagonal element is 0.

After the random vectors are integrated out, the maximized likelihood estimates (MLEs) can be calculated to make inferences about the parameters of interest. Except under some special assumptions, for example, log-log link function with log-gamma random effects (Pulkstenis, et al., 1998), these integrals have no analytical solutions. The marginal likelihood needs to be resolved using numerical approximation which can be computationally intensive, especially for models with multiple random effects. Several common techniques used to approximate this type of integrations are Laplace method (Gao 2004; Skrondal and Rabe-Hesketh 2004), Binomial approximation (Ten Have and Kunselman 1998; Ten Have et al., 2000; Ten Have et al., 2002), Numerical integration using Gauss-Hermite quadrature or adaptive quadrature (Hedeker and Gibbons, 1994; Skrondal and Rabe-Hesketh, 2004) and Monte Carlo method of importance sampling (Salazar, 2004) or Gibbs sampling (Zeger and Karim, 1991), etc.

4. Simulations

Using simulation studies, comparisons are made with respect to parameter estimation between our extended shared random effects model and the model ignoring the baseline. The simulation is set up to have 500 subjects in each iteration and each subject with up to 10 follow-up waves. Depending on one continuous covariate: age and one binary covariate: the presence/absence of an apolipoprotein E-ε4 allele (APOE-4), transition probabilities are estimated by multinomial logistic regression. Considering the models under discussion are complex parametric Markov model involving a large number of parameters, one shared random intercept is considered at this time in order to achieve relative fast likelihood convergence. Three cases are examined: the random intercept following a normal distribution with small variance (σ = 1) and normal distributions with comparatively larger variances (σ = 2 and σ = 3).

To demonstrate the impact of the baseline confounding among cohorts with different baseline outcome structure, three separate simulation studies are implemented. The first simulation assumes a single cohort where all the subjects recruited share the same baseline state of intact cognition, regardless of the covariates of interest (P(y_i0 = 1|X_B, γ) ≡ 1). It is expected that under this circumstance the independence between random effect and baseline state can be reasonably argued and as a result, both models with and without extra likelihood structure should be able to produce similar parameter estimates for the follow-up likelihood component. In the second simulation, we look at the circumstance for a heterogeneous cohort where the probabilities of baseline state follow a multinomial logistic regression, depending on the covariates of interest (P(y_i0 = j|X_B, γ) = π_j). Different from the homogeneous case, we anticipate that the model ignoring the baseline likelihood component is likely to produce more biased parameter estimates associated with the transition probabilities. In the third simulation, we further evaluate the performance of the two models as the number of subjects demented at baseline varies. By assigning different parameters associated with the APOE-4 risk factor to the baseline demented subjects, we generate two cohorts, each with different number of subjects demented at baseline. In addition to the larger bias of the parameter estimates, we expect that such bias tends to intensify as more subjects are demented at baseline, hence excluded from the model without the baseline.

The integral is approximated using the Laplace method. We used the dual quasi-Newton algorithm to optimize the log-likelihood functions, and the method is implemented using SAS^® NLMIXED procedure. The NLMIXED procedure provides a variety of optimization method which ranges from (1) second derivative methods like Newton Raphson where both gradients and Hessians need to be computed for the optimization, (2) first-derivative methods such as quasi-Newton where gradients are required in finding the optimum, and (3) The no-derivative method such as Nelder-Mead simplex, which only the function value is used in optimizing the underlying likelihood function. The quasi-Newton algorithm is the default optimization algorithm because “it provides an appropriate balance between the speed and stability required for most nonlinear mixed model applications” (SAS online doc). The asymptotic relative bias of the parameter estimates are presented in Table 1, Table 2 and Table 3.

Table 1.

Asymptotic relative bias of parameter estimates for homogeneous cohort (base state: 1=Intact cognition)

			σ = 1		σ = 2		σ = 3
Risk Factors	State	θ	With Baseline	Without Baseline	With Baseline	Without Baseline	With Baseline	Without Baseline
Age	2	0.14	3.4%	3.5%	7.5%	7.6%	8.7%	8.8%
	3	0.22	2.8%	2.9%	4.8%	4.7%	4.0%	4.0%
	4	0.20	6.2%	6.2%	6.3%	6.2%	3.7%	3.7%
	5	0.23	1.6%	1.6%	4.0%	3.9%	4.4%	4.4%
APOE-4	2	1.59	3.7%	3.5%	6.2%	6.3%	11.3%	11.5%
	3	1.98	1.6%	1.5%	4.9%	5.0%	7.9%	7.5%
	4	2.06	2.4%	2.2%	9.2%	9.4%	11.3%	11.0%
	5	1.75	5.2%	5.0%	6.5%	6.7%	9.7%	9.3%
Prior state:
Intact Cognition	2	−0.6	5.4%	2.3%	−0.7%	1.2%	−4.9%	−5.9%
	3	−3.0	1.2%	0.5%	0.0%	0.4%	−2.5%	−2.7%
	4	−4.5	5.1%	4.5%	−0.1%	0.2%	−0.7%	−0.9%
	5	−3.0	2.5%	1.8%	1.3%	1.7%	−2.1%	−2.3%
MCI	2	0.3	−18.0%	−12.1%	−9.9%	−13.6%	2.1%	4.3%
	3	−2.7	3.8%	3.1%	1.2%	1.6%	1.9%	1.7%
	4	−2.2	5.0%	4.1%	0.2%	0.7%	−1.9%	−2.2%
	5	−2.5	4.2%	3.4%	−0.2%	0.3%	1.1%	0.9%

States: 2=Mild cognitive impairment I, 3=Global impairment, 4=Dementia, 5=Death

Table 2.

Asymptotic relative bias of parameter estimates for heterogeneous cohort, dependent on covariates of interest (base state: 1=Intact cognition)

			σ = 1		σ = 2		σ = 3
Risk Factors	State	θ	With Baseline	Without Baseline	With Baseline	Without Baseline	With Baseline	Without Baseline
Age	2	0.14	−0.3%	−8.4%	6.1%	−22.6%	10.5%	−46.8%
	3	0.22	0.5%	−4.6%	4.2%	−14.2%	6.5%	−30.4%
	4	0.20	0.2%	−5.5%	4.4%	−16.1%	6.0%	−34.7%
	5	0.23	−0.7%	−5.6%	3.7%	−13.9%	7.6%	−27.7%
APOE-4	2	1.59	2.9%	−4.7%	3.1%	−21.9%	6.1%	−41.7%
	3	1.98	2.2%	−3.9%	3.5%	−16.7%	5.5%	−33.1%
	4	2.06	2.3%	−3.5%	3.3%	−15.9%	5.2%	−31.6%
	5	1.75	2.0%	−4.9%	3.5%	−19.3%	6.7%	−36.9%
Prior state:
Intact Cognition	2	−0.6	6.1%	39.3%	−3.8%	84.0%	−17.1%	140.2%
	3	−3.0	0.5%	7.1%	−0.4%	17.1%	−2.9%	28.4%
	4	−4.5	2.3%	6.6%	1.5%	13.1%	0.3%	21.1%
	5	−3.0	1.5%	8.1%	−0.8%	16.6%	−2.7%	28.5%
MCI	2	0.3	−12.3%	−10.5%	6.9%	7.3%	26.7%	35.4%
	3	−2.7	0.6%	0.4%	−1.2%	−1.3%	−2.7%	−3.7%
	4	−2.2	2.1%	1.8%	−1.2%	−1.3%	−2.0%	−3.2%
	5	−2.5	0.7%	0.5%	−1.8%	−1.8%	−3.1%	−4.1%

States: 2=Mild cognitive impairment I, 3=Global impairment, 4=Dementia, 5=Death

Table 3.

Asymptotic relative bias of parameter estimates for heterogeneous cohort, with different number of demented at baseline (base state: 1=Intact cognition)

		Averaged Baseline Dementia: 14%			Averaged Baseline Dementia: 27%
Risk Factors	State	True β	with baseline	without baseline	True β	with baseline	without baseline
Age	2	0.14	2.2%	−6.6%	0.14	−2.3%	−11.3%
	3	0.22	2.1%	−3.4%	0.22	−2.1%	−7.8%
	4	0.20	0.0%	−6.2%	0.20	−2.6%	−9.0%
	5	0.23	3.2%	−2.1%	0.23	1.4%	−4.0%
APOE4	2	1.59	2.6%	−4.3%	1.59	−4.7%	−16.0%
	3	1.98	0.5%	−5.0%	1.98	−5.1%	−14.2%
	4	2.06	1.5%	−3.8%	2.06	−1.7%	−10.3%
	5	1.75	−1.0%	−7.2%	1.75	−5.8%	−16.0%
Prior=Normal	2	−0.6	−21.5%	12.8%	−0.6	−5.1%	31.0%
	3	−3.0	−2.8%	4.0%	−3.0	2.5%	9.7%
	4	−4.5	13.4%	19.7%	−4.5	8.6%	13.7%
	5	−3.0	−2.4%	4.4%	−3.0	−4.2%	2.9%
Prior=MCI	2	0.30	20.1%	22.9%	0.30	−20.9%	−16.3%
	3	−2.7	−3.4%	−3.7%	−2.7	3.0%	2.5%
	4	−2.2	−7.5%	−7.9%	−2.2	1.8%	1.1%
	5	−2.5	−2.0%	−2.4%	−2.5	2.2%	1.7%
Age (Baseline)	2	0.21	−0.5%	-	0.21	7.5%	-
	3	0.28	1.3%	-	0.28	7.3%	-
	4	0.30	4.7%	-	0.30	4.7%	-
APOE4 (Baseline)	2	0.94	8.0%	-	0.94	−7.4%	-
	3	1.41	10.9%	-	1.41	−3.0%	-
	4	2.12	6.6%	-	4.12	−1.8%	-

States: 2=Mild cognitive impairment I, 3=Global impairment, 4=Dementia, 5=Death

The results for the cohort with homogeneous baseline show that the simulated estimates are almost identical between two models for the parameters associated with age and APOE-4. At σ = 1 for example, the averaged relative biases for the covariate age are both 3.5% and the biases for APOE-4 positive are 3.0% and 3.2% respectively. The biases for the prior states show a little more fluctuation, but are still quite close.

In contrast, for the heterogeneous cohort where the baseline states depend on the model covariates, the maximum likelihood estimates produced by the two models are quite different. In the case of random intercept variance being 1, the relative biases for the covariate age range from −0.7% to 0.5% under our proposed model, while the model ignoring the baseline gives the relative biases ranging from −8.4% to −4.6%. This result indicates that the parameter estimates associated with age are underestimated in the model without baseline structure. This is true across different random intercept variance. A similar conclusion can be made with respect to the covariate APOE-4, in which case the averaged relative biases from the two models are 2.3% and − 4.2% respectively at σ = 1, 3.4% and −18.4% at σ = 2, and 5.9% and −35.8% at σ = 3. Hence, ignoring the baseline is likely to create a serious downward bias which is likely to increase with σ while accounting for the baseline produces a smaller bias.

There are some variations of bias in the maximum likelihood estimation under both models as number of subjects demented at baseline changes. As shown in Table 3, the averaged relative bias under the model with and without the baseline tend to increase as the percentage of subjects demented at baseline gets larger. However such increase is much more conspicuous among those under the model without the baseline. For example, in the case where the cohort has 14% of subjects demented at baseline, the averaged related bias associated with APOE-4 is −5.1% under the model without baseline versus 0.9% under the model with baseline, while as the percentage of baseline demented subjects increases to 34%, the bias changes to −14.1% versus −4.3% between the models.

5. Application: Nun Study

The Nun Study data, a longitudinal study of aging and Alzheimer’s disease funded by the National Institute on Aging will be used to illustrate our proposed model. The dataset consists of a cohort of 678 members of the school sisters of Notre Dame religious congregation (Snowdon et al., 1997). Each participant agrees to allow investigators complete access to their convent archives, participate in near-annual assessments of cognitive and physical function and donate their brain at death. 177 participants are excluded from the analysis because of missing covariates or consent withdrawal. One conspicuous feature of the dataset is that over 10 percent (77) of the subjects are diagnosed with dementia at the baseline visit. Instead of removing those subjects from data analysis, the proposed multi-state Markov model helps to accommodate this baseline information into the likelihood by assuming shared random effects.

The first 10 waves of exam results since 1991 are used in this analysis. The transitions are summarized in Table 4. The covariates of interest are: (1) age in years centered at the median of 88 years, and (2) presence of apolipoprotein E-ε4 allele, a well-known risk factor for dementia.

Table 4.

Number of transitions in the Nun Study

	Current Visit
Prior Visit	Intact Cognition	MCI	GI	Dementia	Deceased
Intact Cognition	520 (65.8%)	179 (22.7 %)	52 (6.6 %)	5 (0.6 %)	34 (4.3 %)
MCI	159 (15.0 %)	629 (59.2 %)	123 (11.6%)	81 (7.6 %)	71 (6.7 %)
GI	15 (4.2 %)	36 (10.0 %)	162 (45.1 %)	67 (18.7%)	79 (22.0 %)
Dementia	0 (0%)	0 (0%)	0 (0%)	77 (27.9%)	199 (72.1%)

The presence of a shared random effect assures the vector of serial observations on a given subject is correlated. When this is restricted to the transitional likelihood (the likelihood without a baseline), only the second through the last observation in this vector are dependent since the transitional likelihood is conditioned on the first observation. On the other hand the model with the baseline correlates all observations in the vector. The simulation studies in Table 2 show that excluding the baseline likelihood from this shared random effect produces estimates of the beta coefficients that are negatively biased and such bias increases as the variance of the shared random effect increases. Table 5 shows how the corresponding parameter estimates for the transition probabilities are consistently underestimated using real data from the Nun Study. In this application we compared three models: the naïve model where we ignore the random effects, an initial random intercept model without the baseline likelihood, and the shared random intercept model with the baseline likelihood.

Table 5.

Parameter estimates for transitions probabilities in the Nun Study data (base state: 1=Intact Cognition)

Risk Factors	State	Naïve Model		Model without baseline		Model with baseline
		estimates	s.e	estimates	s.e	estimates	s.e
Age	2	0.052*	0.0135	0.134*	0.0226	0.160*	0.0216
	3	0.129*	0.0170	0.213*	0.0248	0.240*	0.0242
	4	0.120*	0.0177	0.201*	0.0275	0.229*	0.0270
	5	0.140*	0.0195	0.223*	0.0266	0.250*	0.0260
APOE-4	2	0.548*	0.1785	1.145*	0.3438	1.652*	0.4006
	3	0.863*	0.2160	1.522*	0.3656	2.035*	0.4197
	4	1.199*	0.2206	1.645*	0.3896	2.149*	0.4411
	5	0.651*	0.2561	1.310*	0.3910	1.825*	0.4420
Prior State:
Intact Cognition	2	−1.811*	0.3208	−0.839*	0.3741	−0.414	0.3660
	3	−4.358*	0.3101	−3.350*	0.3657	−2.934*	0.3566
	4	−7.943*	0.5212	−4.831*	0.5696	−4.414*	0.5637
	5	−4.054*	0.3375	−3.044*	0.3894	−2.630*	0.3809
MCI	2	0.576	0.3210	0.397	0.3578	0.315	0.3632
	3	−2.458*	0.2985	−2.643*	0.3381	−2.728*	0.3434
	4	−4.124*	0.2977	−2.190*	0.3570	−2.275*	0.3622
	5	−2.228*	0.3192	−2.465*	0.3565	−2.548*	0.3615
σ		NA	NA	1.638*	0.2097	2.071*	0.1973

^*significant at P < 0.05

States: 2=Mild cognitive impairment I, 3=Global impairment, 4=Dementia, 5=Death

The results from Table 5 indicate that estimates under models with and without the baseline likelihood component are different. For example, consider the fixed effect of apolipoprotein E-ε4 allele (APOE4=1). It has been well documented that the presence of APOE4 increases the chance of cognitive impairment. Under the naïve model, the MLEs for APOE4=1 are (0.548, 0.863, 1.199, 0.651), which means that keeping other covariates constant, the odds ratio of having APOE4 present for transitions from intact cognition to MCI is 1.73, intact to global impairment is 2.37, intact to dementia is 3.32 and intact to death is 1.92. In comparison, the odds ratios are 3.14, 4.58, 5.18 and 3.71 under the model without the baseline likelihood component and 5.22, 7.65, 8.58, 6.20 under the model with the baseline component. We can see that although the effect of APOE4 is significant in all three models, the magnitude of odds ratios under the new model is larger.

6. Higher order Markov chains

The model introduced in this paper can be applied to higher order chains. Without loss of generality, in a second order case, the transition probability matrix P_rsv has a hierarchical structure P_rsv = (P_r=1,sv P_r=2,sv P_r=3,sv)^t where each P_r=i,sv, i = 1,2,3 is a transition sub-matrix corresponding to the second immediate prior state r. The parameterization of transition probabilities is similar to the first order case. The individual transition probability P_rsv still maintains the polytomous logistic structure while the three first order sub-matrices are only different in parameters associated with r. In the first order Markov chain structure, the parameters ξ_h (s) indicate the immediate prior states s, while in the second order case, it needs additional components, say ζ_h (r), to indicate second immediate prior states r. Because of this hierarchical structure, ζ_h (r) differentiates among sub-matrices, and ξ_h (s) differentiates among rows within each sub-matrix.

The likelihood for the second order Markov model further breaks down the joint distribution into three likelihood components with shared random effects. The joint distribution can be factorized as the following

$$\begin{array}{l}f(y_{i0},y_{i1},y_{i2},\dots ,y_{i{n}_i}\mid \mathit{\gamma })\\ =\underset{2\text{nd}-\text{order}-\text{Follow}-\text{up}}{\underbrace{f(y_{i2}\mid y_{i1},y_{i0},\mathit{\gamma })f(y_{i3}\mid y_{i2},y_{i1},\mathit{\gamma })\dots f(y_{i{n}_i}\mid y_{i{n}_i-1},y_{i{n}_i-2},\mathit{\gamma })}}\underset{1\text{st}-\text{order}-\text{follow}-\text{up}}{\underbrace{f(y_{i1}\mid y_{i0},\mathit{\gamma })}}\underset{\text{Baseline}}{\underbrace{f(y_{i0}\mid \mathit{\gamma })}}\end{array}$$

and the likelihood for a particular subject is

$$L(\mathit{\Theta },\mathit{K},\mathit{\Phi }\mid \mathit{X})=\underset{2\text{nd}-\text{order}-\text{follow}-\text{up}}{\underbrace{\int \prod _{k=2}^{n_i}{P}_{y_{ik-2,}{y}_{ik-1,}{y}_{ik}}(\mathit{\Theta }\mid \mathit{X},\mathit{\gamma })}}\underset{1\text{st}-\text{order}-\text{follow}-\text{up}}{\underbrace{P_{y_{i1},y_{i0}}(\mathit{K}\mid \mathit{X},\mathit{\gamma })}}\underset{\text{baseline}}{\underbrace{{\pi }_{y_{i0}}(\mathit{\Phi }\mid {\mathit{X}}_B,\mathit{\gamma })}}\underset{\text{random}\text{effect}}{\underbrace{h(\mathit{\gamma })d\mathit{\gamma }}}$$

The variance covariance structure of the random effect distribution does not have to be the same across the likelihood components. It is also possible for these components to partially share the random effects. Take the random intercept and random slope model for instance: the baseline component shares only the random intercept with the two follow-up components, which share an extra random slope.

In theory this model applies to an arbitrarily higher order Markov chain, while in practice the number of parameters that need to be estimated can add up quickly which, in combination with the numerical integration of random effects, might produce the computational burdens in the likelihood optimization (refer to Table 6 for example).

Table 6.

Fit statistics for models assuming higher order chains, the Nun Study data

	Fit Statistics
	1st order	2nd order	3rd order
−2 Log Likelihood	5936.7	5812.3	5747.4
AIC (smaller is better)	5996.7	5918.3	5925.4
AICC (smaller is better)	5997.5	5920.4	5931.5
BIC (smaller is better)	6123.2	6141.8	6300.7
# of parameters	30	53	89

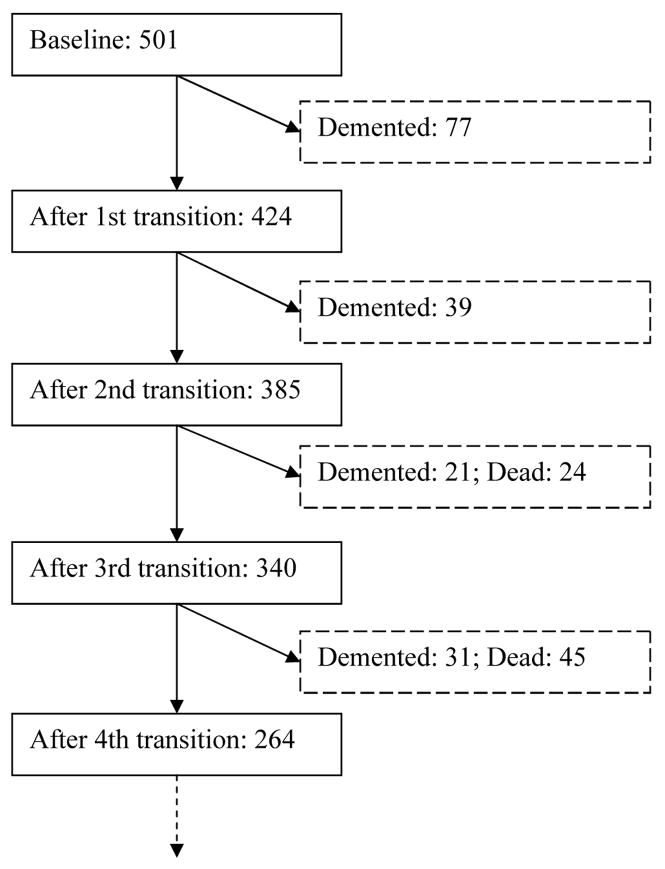
The advantage of this approach is that; first, it helps to reduce the possible confounding bias that could occur otherwise. This is especially the case when higher order chains are assumed. Referring to the Nun Study data, the flow diagram indicates that there are 77 nuns demented at baseline and after the first follow-up wave, 39 more are demented. In a second order chain scenario, a total of 116 subjects would have to be removed from the analysis, accounting for over 20 percent of the total available data.

Second, the likelihood based approaches facilitate the inferential procedures like common likelihood ratio tests. These can be used to test model fitness, in particular, the hypothesis about the orders of a particular chain. We fit a second and third order Markov models using the Nun Study data. As shown in Table 6, all the fit statistics suggest that the third order model is no better than the second order model, and the likelihood ratio tests as well as the Akaike’s information criterion (AIC) indicate that the second order model might be better than the first order model, while the Bayesian information criterion (BIC) supports the first order model. This mixed result points out that the approximation of the joint distribution f(y_i0, y_i1|γ) using the product of f(y_i1|y_i0, γ) and f(y_i0|γ) may be oversimplified in practice and we are looking for a single joint density for y_i0 and y_i1. Meanwhile the first order assumption in the Nun Study data may also deserve further examination.

Moreover, by modeling the transition among states with a Markov structure, the one-step transition probability matrices constructed based on the parameter estimates provide additional information with respect to the mean time to absorption as well as the odds of absorption in competing absorbing states. This is particularly useful in the study of chronic diseases like Alzheimer’s disease where researchers are interested in the probability of disease onset before dying given a set of risk factors such as age, education, and genetic status.

7. Conclusion and Future Work

Subjects in the Nun Study do not share the same baseline state. Among 501 subjects used for analysis, 128 of them had intact cognition at baseline, 249 had MCI, 47 had global impairment and 77 were demented. Although a model without a baseline likelihood component could be considered for a cohort with some homogeneous baseline states¹, the diversified states at baseline for subjects in the Nun Study make it important to incorporate the baseline outcomes into the likelihood construction. The proposed multi-state Markov model helps to accommodate this baseline information into the likelihood by assuming shared random effects. Since all the risk factors considered in the application to the Nun Study are the most established risk factors, the comparison of the maximum likelihood estimates shows difference only in magnitude rather than significance, it is feasible however that other risk factors with important but weaker association with cognitive status transitions might be missed without accounting for the baseline information. Moreover, from an epidemiological perspective, without including all baseline information, the prevalence (baseline) cases tend to be different from the incidence (follow-up) cases, which is likely to produce selection bias into the analysis.

The analysis of panel data with categorical outcomes is not a straightforward task. One of the strengths of the approach suggested in this manuscript for constructing a likelihood function for such data is that it assumes a Markov model for transitions among states. This makes it easy to incorporate the baseline status of the individual into the likelihood computation provided we introduce a shared random effect to assure the elements in the entire vector of observations on an individual are correlated. The arithmetic is no more complicated than when the baseline is ignored since we continue to rely on standard statistical software (Procedure NLMIXED in SAS) to fit the expanded likelihood to the data as evidenced by the Nun study data. However, there are some limitations to this approach since this software relies on numerical quadrature techniques. One limitation concerns k, the number of states in the process, or r, the number of risk factors investigated. As either k or r increase the number of unknown parameters increases making it difficult to achieve convergence of the likelihood to its maximum. One reason for this is that as k increases the possibility of encountering sparse cells in the one step transition matrix increases. The one step transition matrix links the covariate to the transition using a polytomous logistic model and convergence problems arise since that model is sensitive to sparse cells. Similarly as r increases the one step matrix gets partitioned according to different combinations of the risk factors again promoting the possibility of encountering sparse cells.

The likelihood construction in this model is based on the first-order Markov assumption, namely that the conditional distribution of the current outcome for a particular subject depends on the previous outcomes only through the most recent one. Whether the data maintains this Markov property directly affects the validity of maximum likelihood estimation. The verification of this assumption is non-ignorable. As in the general GLMM model, conditioning on both measured and unobserved latent variables makes the subject-specific coefficient difficult to interpret, especially when the involved covariates do not vary within individuals. According to Heagerty (1999), these coefficients measure the contrast in covariates when the random effects are held equal, but the random effects are not directly observed. The latent variable assumptions determine what values of random effect are equivalent; the magnitude and interpretation of the fixed effects therefore depend entirely on these assumptions. As a result the model tends to produce biases in regression estimates when the distribution of random effects has been misspecified (Litiere et al., 2007). This raises a new set of issues involving methods of model diagnostics under GLMMs, in particular the analysis of random effects misspecifications, which have not yet been thoroughly explored in the literature.

Figure 1.

Flow diagram of Nun Study Data (First four follow-up waves)