Influence of visual scene velocity on segmental kinematics during stance

Abstract

We investigated how the velocity of anterior-posterior movement of a visual surround affected segmental kinematics during stance. Ten healthy young adults were exposed to sinusoidal oscillation of an immersive virtual scene at 5 peak velocities ranging from 1.2 to 188 cm/s at each of 4 frequencies: 0.05, 0.1, 0.2 and 0.55 Hz. Root mean square (RMS) values of head, trunk, thigh and shank angular displacements were calculated. RMS values of head-neck, hip, knee and ankle joint angles were also calculated. RMS values of head, trunk, thigh and shank displacements exhibited significant increases at a scene velocity of 188 cm/s when compared with lower scene velocities. RMS values of hip, knee and ankle joint angles exhibited significant increases at scene velocities of 125 and 188 cm/s when compared with lower scene velocities. These results suggest that visual cues continued to drive postural adjustments even during high velocity movement of the virtual scene. Significant increases in the RMS values of the lower-limb joint angles suggest that as visually-induced postural instability increased, the body was primarily controlled as a multi-segmental structure instead of a single-link inverted pendulum, with the knee playing a key role in postural stabilization.

Introduction

Visual information about one's spatial orientation can influence postural behavior during stance. When an individual observes motion of the visual surround, the perception is that the individual is moving in a direction opposite to the visual motion. As a consequence, the individual generates compensatory postural adjustments in the direction of the visual surround motion [1].

In daily-life one can encounter many instances where large velocity movement of the visual surround does not represent the individual's true body motion, for example, when navigating street traffic. Previous studies that have investigated the effect of large visual surround velocity on postural stability have reported diverse findings. Cunningham et al. [2] observed that the amplitude of head displacement increased as the visual surround velocity increased. Other studies, however, reported that visual surround velocity had no effect on the head [3] and center of pressure displacements [4]. Furthermore, it is not known how exposure to large velocity movement of the visual surround influences inter-segmental kinematics. Although Cunningham et al. [2] investigated the effect of visual surround velocity on postural behavior, they only reported head displacements. Previous report in the literature has demonstrated that movement of the visual surround elicited larger motion at the hip rather than the ankle when compared with that from a stationary surround [5], but it remains to be investigated how changes in postural stability elicited by increasing velocities of visual surround motion modulate the segmental biomechanics governing postural control.

To understand how visual surround motion influenced segmental kinematics, we exposed healthy young adults to anterior-posterior (AP) motion of an immersive virtual scene over a wide range of velocities and frequencies. We hypothesized that the amplitude of segmental displacements would increase with an increase in the virtual scene velocity when the temporal frequency of the scene oscillation was kept constant. We also hypothesized that such an increase in visually-induced postural instability would modulate subjects' inter-segmental kinematics. That is, at increasing scene velocities, subjects would exhibit a greater change in their hip rather than ankle joint angle.

Methods

Ten healthy young adults (age: 20-34 years) participated in the experiment. Subjects had no history of neurological or musculoskeletal disorders and had normal or corrected-to-normal vision. Subjects gave their informed consent in accordance with the guidelines set by the Institutional Review Board of Feinberg School of Medicine, Northwestern University.

Subjects viewed a virtual environment projected via a stereo-capable projector (Electrohome Marquis 8500) onto a 2.6 m × 3.2 m back-projection screen. The virtual scene consisted of a 30.5 m wide by 6.1 m high by 30.5 m deep room containing round columns with patterned rugs and painted ceiling. Beyond the virtual room was a landscape consisting of mountains, meadows, sky and clouds. Subjects were instructed to wear liquid crystal stereo shutter glasses (Stereographics, Inc.) which separated the field sequential stereo images into right and left eye images. The shutter glasses limited the subject's horizontal field of view (FOV) to 100° and 55° for the vertical FOV. Reflective markers (Motion Analysis, Inc.) attached to the shutter glasses provided real-time orientation of the head that was used to compute correct perspective and stereo projections for the virtual scene. Consequently, virtual objects retained their true perspective and position in space regardless of the subject's movement. The display system latency measured from the time a subject moved to the time a new stereo image was displayed was 20 – 36 ms. On verbal enquiry, all subjects reported that they perceived the virtual scene as a three-dimensional stereo image.

Subjects stood in front of the virtual scene with their feet shoulder-width apart and their arms bent approximately 90° at their elbows. The location of subjects' feet on the support surface was marked; subjects were instructed to stand at the same location at the beginning of each trial. During each trial, subjects were asked to maintain an upright posture while looking straight ahead at the virtual scene.

Subjects were exposed, in random order, to AP sinusoidal oscillation of the virtual scene at 5 peak velocities: 1.2, 3.7, 31, 125 and 188 cm/s at each of 4 frequencies: 0.05, 0.1, 0.2 and 0.55 Hz. The velocities of virtual scene motion were chosen from a range that is known to elicit the largest amplitude of illusory self-motion in humans [6]. The frequencies of virtual scene oscillation were similar to those used by Dijkstra et al. [7]. At each frequency, the amplitude of sinusoidal scene motion was changed to achieve the desired peak velocity as shown in Table 1. In addition, subjects experienced a control condition where the motion of the virtual scene occurred only when the subject's head moved and this scene motion was equal in amplitude and opposite to the direction of the subject's head displacement (natural visual feedback - NV). In trials with large amplitude perturbation of the virtual scene, this addition of subject's head displacement to the scene motion was insignificant and unobservable to the subjects. Subjects experienced each visual condition once. Trials lasted for 70 s; in trials with a driving visual stimulus, 5 s of NV preceded and followed the sinusoidal motion of the virtual scene.

Table 1.

Amplitudes used to generate peak velocities of 1.2 (second column from the left), 3.7 (third column), 31 (fourth column), 125 (fifth column) and 188 (sixth column) cm/s at different frequencies of virtual scene oscillation.

Frequency of virtual scene motion (Hz)	Amplitude of virtual scene motion (cm)
0.05	4	12	100	400	600
0.1	2	6	50	200	300
0.2	1	3	25	100	150
0.55	0.36	1.1	9.1	36.4	54.5

Reflective markers were placed bilaterally on the second digit of the foot, ankle joint, knee joint, greater trochanter of hip, thigh, shoulder joint, elbow joint, wrist joint and index-finger of the hand. Markers were also placed on the head, first thoracic and fifth lumbar vertebrae. A six infra-red camera (Motion Analysis, Inc.) system was used to capture the displacement of the reflective markers at 120 Hz. Displacement data of the markers was low pass filtered using a fourth order Butterworth digital filter with a cutoff at 6 Hz. Vertical and fore-aft displacement of the markers was used to compute the angular displacement of the body segments. Head angular displacement was calculated from the data of the head and thoracic spine markers; trunk angular displacement was calculated from the data of the shoulder and lumbar spine markers; thigh angular displacement was calculated from the data of the hip and thigh markers; shank angular displacement was calculated using the data of the knee and ankle joint markers; foot angular displacement was calculated using the data of the ankle and foot markers. Head-neck joint angle was computed from the angular displacement of the head and trunk segments; hip joint angle was computed from the angular displacement of the trunk and thigh segments; knee joint angle was computed from the angular displacement of the thigh and shank segments; ankle joint angle was computed from the angular displacements of the shank and foot segments. Root mean square (RMS) values of head, trunk, thigh and shank angular displacements were calculated. RMS values of head-neck, hip, knee and ankle joint angles were also calculated. Before computing the RMS values, the mean was subtracted from the respective time-series. In addition, power spectra of the trunk angular displacement were computed using the fast fourier transform “FFT” routine in Matlab™ (Mathworks, Inc.) [8]. Pearson's cross-correlation coefficient between virtual scene and head displacements was also computed. The angular displacements of body segments and joint angles were computed as per the guidelines outlined by Winter [9].

Statistical analyses were carried out using Minitab® (Minitab, Inc.). A two-way ANOVA (frequency × velocity) with repeated measures was performed on the RMS values of the segmental displacements and joint angles. Two-way ANOVA was also used to compare the cross-correlation coefficient between virtual scene and head displacements. When ANOVA indicated significant effect of an independent variable, post-hoc Bonferroni multiple comparisons were performed to determine significant differences between various conditions.

Results

Angular displacements of the head, trunk and shank segments of a representative subject during NV and virtual scene oscillation at 0.2 Hz are shown in Figure 1a. With a scene velocity of 188 cm/s, the subject exhibited prominent oscillations of the head, trunk and shank at the driving frequency (0.2 Hz). Moreover, the amplitudes of these oscillations were larger than those observed with a scene velocity of 3.7 cm/s and NV. Figure 1b shows the power spectra of the trunk angular displacement averaged across subjects when they viewed NV and virtual scene oscillation at 0.2 Hz. With a scene velocity of 188 cm/s, there was a dramatic increase in the power at the stimulus frequency when compared with a scene velocity of 3.7 cm/s and NV. In addition, at a scene velocity of 188 cm/s, there were marginal increases in the power at non-stimulus frequencies, that is at frequencies not contained in the visual stimulus.

Figure 1.

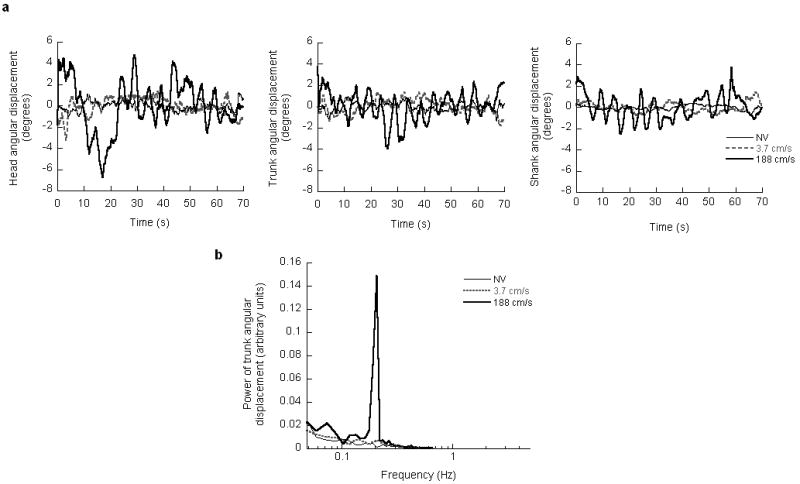
a: Head, trunk and shank angular displacements of a representative subject during natural visual feedback (NV) and virtual scene oscillations at 0.2 Hz. b: Power spectra of trunk angular displacement averaged across subjects during NV and virtual scene oscillation at 0.2 Hz.

There was a significant effect of virtual scene velocity on the RMS values of the head (F(5,45) = 2.82, p<0.05), trunk (F(5, 45) = 9.4, p<0.0001), thigh (F(5, 45) = 7.17, p<0.0001) and shank (F(5, 45) = 8.61, p<0.0001) displacements (Figure 2a). Table 2 presents the t-statistics and p values associated with Bonferroni multiple comparisons performed on the RMS values of the segmental displacements. As indicated in Table 2, RMS value of head displacement exhibited significant increase at a scene velocity of 188 cm/s when compared with 1.2 cm/s. RMS value of trunk displacement exhibited significant increase at 188 cm/s when compared with NV, 1.2, 3.7 and 31 cm/s. RMS values of thigh and shank displacement at 3.7 and 31 cm/s significantly increased when compared with NV. RMS values of thigh and shank displacement at 125 and 188 cm/s also exhibited significant increases when compared with NV and 1.2 cm/s. There was no influence of frequency on the RMS values of segmental displacements; no interaction was observed between the scene velocity and frequency.

Figure 2.

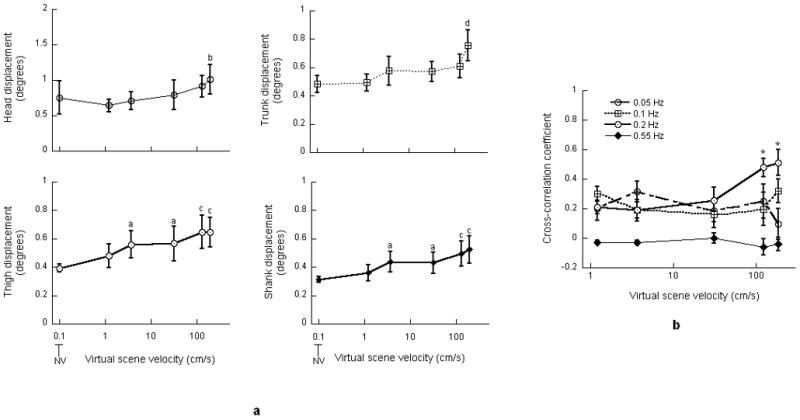
a: Root mean square values of the head, trunk, thigh and shank angular displacement. a indicates significant increase when compared with NV; b indicates significant increase when compared with 1.2 cm/s; c indicates significant increase when compared with NV and 1.2 cm/s; d indicates significant increase when compared with NV, 1.2, 3.7 and 31 cm/s. b: Cross-correlation coefficient between virtual scene and head displacements. * indicates significant increase when compared with scene velocities of 1.2 and 3.7 cm/s. Error bars indicate the standard error of the mean.

Table 2.

T-statistics and p values of Bonferroni multiple comparisons performed on the root mean square values of segmental angular displacements and joint angles. p indicates significant increase with respect to NV, q indicates significant increase with respect to 1.2 cm/s, r indicates significant increase with respect to 3.7 cm/s and s indicates significant increase with respect to 31 cm/s.

	Velocity of virtual scene motion (cm/s)
Variable	1.2	3.7	31	125	188
Head segment	-	-	-	-	t45 = -3.202, p<0.05 q
Trunk segment	-	-	-	-	t45 = -5.987, p<0.001 p
					t45 = -5.761, p<0.001 q
					t45 = -3.909, p<0.005 r
					t45 = -4.014; p<0.005 s
Thigh segment	-	t45 = -3.214, p<0.05 p	t45 = -3.336, p<0.05 p	t45 = -4.877, p<0.001 p	t45 = -4.858, p<0.001 p
				t45 = -3.213, p<0.05 q	t45 = -3.195, p<0.05 q
Shank segment	-	t45 = -3.211, p<0.05 p	t45 = -3.078, p<0.05 p	t45 = -4.754, p<0.001 p	t45 = -5.496, p<0.001 p
				t45 = -3.538, p<0.05 q	t45 = -4.288, p<0.001 q
Head-neck joint	-	-	-	-	-
Hip joint	-	-	-	t45 = -3.233, p<0.05 p	t45 = -3.178, p<0.05 p
Knee joint	-	t45 = -3.149, p<0.05 p	t45 = -3.091, p<0.05 p	t45= -4.299, p<0.001 p	t45 = -3.784, p<0.005 p
Ankle joint	-	-	-	t45 = -3.913, p<0.005 p	t45 = -4.393, p<0.001 p
				t45 = -3.702, p<0.005 q	t45 = -4.182, p<0.001 q

Two-way ANOVA performed on the cross-correlation coefficients revealed a significant interaction between the virtual scene velocity and frequency (F(12, 108) = 2.43, p<0.01). Consequently, the correlation coefficients were separately analyzed at each frequency of scene oscillation. At 0.05, 0.1 and 0.55 Hz there was no effect of scene velocity on the cross-correlation coefficient. However, at 0.2 Hz, the velocity of scene motion exerted a significant effect (F(4, 36) = 6.23, p<0.005) on the cross-correlation coefficient (Figure 2b). The cross-correlation coefficient at a scene velocity of 188 cm/s was significantly greater when compared with 1.2 and 3.7 cm/s (t₃₆ = 3.453 and p<0.05, t₃₆ = -3.696 and p<0.01, respectively). The cross-correlation coefficient at scene velocity of 125 cm/s also exhibited significant increases when compared with 1.2 and 3.7 cm/s (t₃₆ = 3.07 and p<0.05, t₃₆ = 3.314 and p<0.05, respectively).

There was a significant effect of scene velocity on the RMS values of the hip (F(5, 45) = 3.99, p<0.005), knee (F(5, 45) = 4.57, p<0.005) and ankle (F(5, 45) = 6.81, p<0.0001) joint angles (Figure 3). Table 2 also presents the t-statistics and p values associated with Bonferroni multiple comparisons performed on the RMS values of the joint angles. As indicated in Table 2, RMS values of the hip joint angle exhibited significant increases at scene velocities of 125 and 188 cm/s when compared with NV. RMS values of the knee joint angle significantly increased at scene velocities of 3.7, 31, 125 and 188 cm/s when compared with NV. RMS values of ankle joint angle at 125 and 188 cm/s exhibited significant increases when compared with NV and 1.2 cm/s. There was no effect of frequency on the RMS values of the joint angles; no interaction was observed between the scene velocity and frequency. There was no change in the RMS values of head-neck joint angle at different scene conditions.

Figure 3.

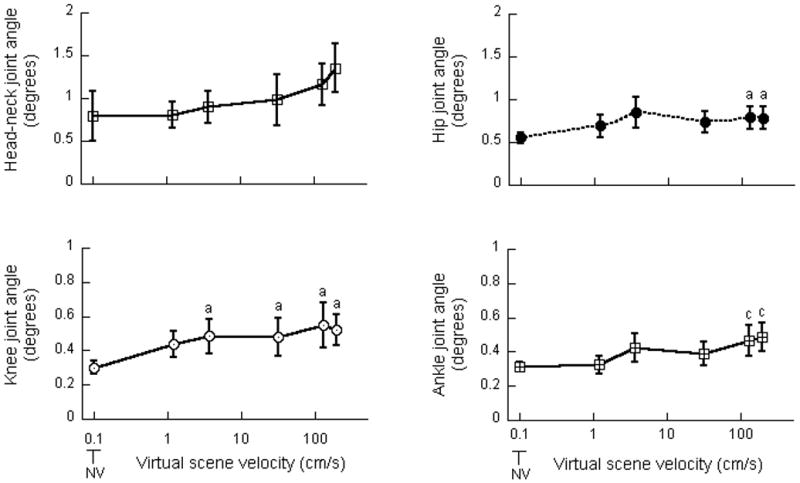
Root mean square values of head-neck, hip, knee and ankle joint angles. a indicates significant increase when compared with NV; c indicates significant increase when compared with NV and 1.2 cm/s. Error bars indicate the standard error of the mean.

Discussion

The results reported in this article indicate that at each temporal frequency, peak velocity and/or amplitude of sinusoidal motion of a virtual scene exerted significant influence on the segmental kinematics. Such changes in the amplitude of segmental displacements could be due to an increase in the scene velocity or scene amplitude or both. However, previous evidence in the literature implicates visual scene velocity rather than amplitude as the main factor that influences postural behavior. Lestienne et al. [10] examined subjects' ankle joint angle when they were exposed to unidirectional forward motion of the visual scene at constant velocities ranging from 2.75 to 200 cm/s. They found that as the visual scene velocity increased, subjects exhibited a logarithmic increase in the amplitude of their ankle joint angle. Since Lestienne et al. [10] used constant scene velocities without manipulating the frequency and amplitude, it follows that the observed increase in the amplitude of postural adjustments was due to an increase in the scene velocity. In view of this evidence, we believe that, despite the large increases in scene amplitude, the postural behavior of our subjects was primarily influenced by the increased velocity of visual scene motion when the period of scene oscillation was kept constant.

Increases in the amplitude of segmental displacements indicate that large velocity movement of the virtual scene elicited larger postural adjustments when compared with smaller scene velocities. Previously, Cunningham et al. [2] also observed an increase in the amplitude of postural adjustments when the virtual scene velocity increased. In their study, Cunningham et al. exposed subjects to virtual scene oscillations at 0.2 Hz and peak velocities ranging from 3.14 to 100 cm/s. They observed that as the scene velocity increased, peak-to-peak amplitude of subjects' head displacement increased. Our results not only corroborate their findings, but also demonstrate that scene velocity-dependent increases in postural adjustments persist at velocities higher than those investigated by Cunningham et al.

We also examined the cross-correlation between virtual scene and head displacements. At 0.2 Hz oscillation of the scene, significant increases were observed in the cross-correlation coefficient as the magnitude of virtual scene motion increased. These results corroborate the previous findings of Cunningham et al. [2] and suggest that the temporal relationship between the visual stimulus and postural response changed at higher magnitudes of visual surround motion even when the stimulus frequency was kept constant. These results are suggestive of changes in the phase of visually-induced postural responses [11] and emphasize the non-linear nature of postural adjustments elicited by large visual surround velocities [12].

We hypothesized that as postural instability increased at higher scene velocities, subjects would exhibit an increase in their hip rather than ankle joint angle. However, significant increases were observed in the RMS values of the hip, knee and ankle joint angles at scene velocities of 125 and 188 cm/s when compared with lower scene velocities. Such an increase in the lower-limb joint angles suggests that at increasing scene velocities, the body was primarily controlled as a multi-segmental structure that required additional stabilization at the hip and knee.

These results support the emerging view in the literature that even during quiet stance, the human body behaves as a multi-segmental pendulum rather than a single-link inverted pendulum [5, 13, 14]. Furthermore, these results corroborate previous reports of Keshner et al. [5] who observed increased motion at the hip when subjects viewed movement of the visual surround. However, previous studies have not reported a significant role of the knee in postural stabilization during quiet stance. Nevertheless, the role of the knee in maintaining postural stability when the body is exposed to support surface perturbations has been recognized. Nijhuis et al. [15] examined the joint kinematics of young healthy subjects in response to support surface rotations with their knees either unrestrained or restrained with a cast. With the cast on, subjects exhibited significant changes in their ankle, hip and arm movement strategies indicating that the knee played an important role in body stabilization.

Our findings of a significant impact of increasing scene velocity on posture are in direct contrast to those reported by van Asten et al. [3] and Masson et al. [4]. van Asten et al. [3] did not observe any change in the amplitude of subjects' head displacement during exposure to scene oscillation at 0.2 Hz and peak velocities ranging from 25 to 376 cm/s. Similarly, Masson et al. [4] did not observe any change in the displacement of the center of pressure during scene oscillation at 0.1738 Hz and peak velocities ranging from 11 to 176 cm/s.

The differences between the results reported in this article and previous findings could be due to the characteristics of the virtual scene used in the experiments. While van Asten et al. [3] and Masson et al. [4] used a virtual scene that comprised of an abstract black and white pattern, we used a texture-mapped virtual scene that was comprised of visually-polarized objects such as sky, patterned rugs and mountains. It is likely that the visual polarity cues provided by such a virtual scene contributed to the strong postural reactions exhibited by our subjects. In fact, Howard et al. [16] demonstrated that visual polarity of the environment influences the magnitude of subject's response to visual stimulus: motion of an environment filled with visually-polarized objects induced greater tilt in subject's perceived body orientation when compared to similar motion of an environment that was lacking in visual polarity cues. Moreover, in our experiments, subjects experienced binocular stereo vision with a wide FOV (100° in the horizontal direction and 55° in the vertical direction). In contrast, subjects tested by van Asten et al. experienced monocular non-stereo vision of the left eye with FOV of 80°. Similarly, subjects tested by Masson et al. experienced monocular non-stereo vision of the right eye with FOV of 40°. Binocular stereo vision combined with wide FOV, used in our experiments, could also have contributed to the strong influence of visual scene motion on postural adjustments as stereoscopic vision and large field of view are known to amplify the effect of visual stimulus on subject's response [17, 18]. We believe that our choice of experimental conditions allowed us to investigate visually-induced body movements in a realistic setting since the world around us is three-dimensional and filled with visually-polarized objects.

There was a dramatic increase in the power of the trunk displacement at the stimulus frequency when subjects viewed large velocity movement of the visual scene. This increase in the power at the stimulus frequency suggests that large visual scene velocity exerted greater impact on the segmental kinematics when compared with smaller velocities. Interestingly, the power at the non-stimulus frequencies also increased even though these frequencies were not contained in the visual stimulus, reemphasizing the non-linear nature of postural adjustments elicited by large visual surround velocities [5, 19]. Overall these findings suggest that during large velocity movement of the visual surround, misleading visual cues that were not accurate indicators of body orientation were meaningfully integrated into the internal body schema [20], such that they influenced subjects' perceived spatial orientation [21] and consequently, played an important role in postural control. There is evidence that visual cues can similarly drive perceptual and postural responses. In our experiment the range of virtual scene velocities that elicited largest segmental displacement is similar to the range of velocities that elicited largest perception of self-motion [6]. Berthoz et al. [6] examined subjects' perceived self-motion when they viewed uni-directional backward motion of the visual scene at constant velocities ranging from 0 to 360 cm/s. Berthoz et al. observed that the magnitude of perceived self-motion increased with an increase in the scene velocity until it saturated at a velocity of 100 cm/s. This maximum amplitude of perceived self-motion persisted at scene velocities as high as 260 cm/s. While we did not measure subjects' perceived self-motion, earlier studies in the literature have reported a dependence of postural adjustments on the perception of self-motion. Thurrell et al. [22] recorded the center of pressure displacement and perception of self-/ object-motion when standing individuals were exposed to visual scene rotation about their line of sight. They found that the displacement of the center of pressure increased when subjects perceived self-motion as opposed to object motion. If subjects tested in our experiment only perceived object motion, there should not have been any change in their segmental displacements at increasing scene velocities. However, subjects exhibited a significant increase in their segmental displacements which suggest that subjects might have experienced illusory self-motion whose magnitude increased with an increase in the scene velocity. Taken together with previous findings, our results suggest that similar sensory-integration mechanisms may govern perception of spatial orientation and postural control.

Finally, the findings reported here raise questions pertinent to the control of posture in elderly people. Previous reports have indicated that elderly are more vulnerable to misleading visual cues than young individuals [23]. However, aging is often associated with increased rigidity of the lower-limb joints [24]. It is not clear if the increased postural instability in elderly on observance of conflicting visual cues is due to a change in sensory-integration or an inappropriate selection of inter-segmental kinematics or both. Future investigations using multi-segmental analysis could elaborate on how aging influences the neural as well as biomechanical mechanisms of postural control during stance.