Figure 1.

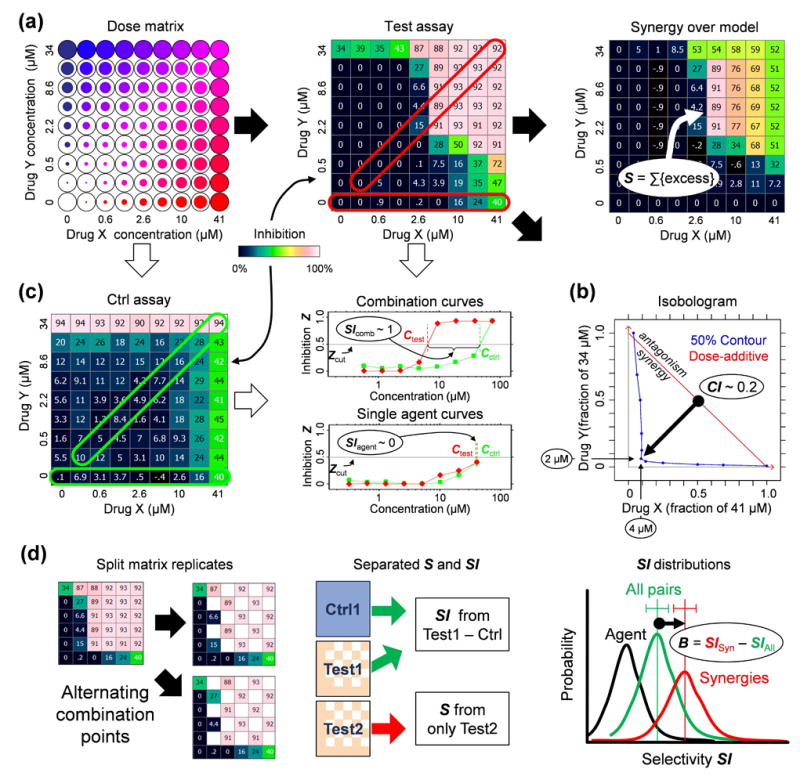
Measuring the selectivity bias. (a) Determining synergy using dose matrix data. A factorial dose matrix samples all mixtures of two serially-diluted single agents’ concentrations. Phenotypic measurements, like inhibition Z relative to vehicle-treated samples, can be visualized over the matrix using a color scale, and each data point be compared to expected values via a null model (e.g., the highest-single-agent²⁴ or dose-additive⁴⁷ model, see Methods) derived from the single agent data along the left and bottom edges of the matrix. The synergy score S = ln f_X ln f_Y Σ_doses max(0,Z_data) (Z_data − Z_model) sums up the excess inhibition over the HSA model with weights to account for drug dilution factors f_X,f_Y, and favor synergy at high inhibition levels. (b) Synergy can also be described using an isobologram, which compares the doses along an equal-effect contour (in blue) for a chosen inhibition level Z_cut (here 50%) to the contour (red) for dose-additivity. The combination index²⁹ CI = (C_X/IC_X) + (C_Y/IC_Y) measures the fractional shift (black arrow) between the most potent mixture’s doses C_X,C_Y and the single agents’ inhibitory concentrations IC_X,IC_Y. In this example, to reach 50% inhibition, only 4 μM of Drug A and 2 μM of Drug B were required in combination, compared to >41 μM and >34 μM for the single agents. (c) Selectivity is determined from the responses in two assays (“test” and “ctrl”). Single agent (horizontal frames) and fixed dose ratio combination curves (diagonal frames) are extracted from both dose matrices. For Z_cut, effective concentrations C_test,C_ctrl (top dose if agents don’t reach Z_cut) are determined in both assays (colors match frames in matrices) for all extracted curves, and the selectivity index SI = log₁₀(C_ctrl/C_test) measures potency shifts between assays, where SI = 1 implies a tenfold potency ratio favoring the test assay. The synergistic selectivity for a single combination can be described using ΔSI = SI_comb − SI_agent or ΔCI = CI_ctrl − CI_test based on the most selective diagonal curve and the most effective single agent in the test assay. (d) The selectivity bias was determined by comparing SI shifts across many combinations. To avoid spurious correlations due to noise, each test matrix was split into independent copies (see Methods), one to calculate SI and the other for S. The SI distributions across the screen were compared for all combinations (green distribution) and those with S > S_cut (green), and the selectivity bias B is measured as the difference between the mean SI values for the two distributions. For reference, we also show the SI distributions of the more effective single agent in black.