A complex-centric view of protein network evolution

Abstract

The recent availability of protein–protein interaction networks for several species makes it possible to study protein complexes in an evolutionary context. In this article, we present a novel network-based framework for reconstructing the evolutionary history of protein complexes. Our analysis is based on generalizing evolutionary measures for single proteins to the level of whole subnetworks, comprehensively considering a broad set of computationally derived complexes and accounting for both sequence and interaction changes. Specifically, we compute sets of orthologous complexes across species, and use these to derive evolutionary rate and age measures for protein complexes. We observe significant correlations between the evolutionary properties of a complex and those of its member proteins, suggesting that protein complexes form early in evolution and evolve as coherent units. Additionally, our approach enables us to directly quantify the extent to which gene duplication has played a role in the evolution of complexes. We find that about one quarter of the sets of orthologous complexes have originated from evolutionary cores of homodimers that underwent duplication and divergence, testifying to the important role of gene duplication in protein complex evolution.

INTRODUCTION

Recent technological advances, such as yeast two-hybrid screens (1) and co-immunoprecipitation (coIP) assays (2), enable the systematic characterization of protein–protein interaction (PPI) networks across multiple species. Large-scale PPI networks are currently available for human and most model species (3–5).

To date, evolutionary analysis of protein network data has been mostly limited to comparison of single interactions (6), or whole networks (7). In the context of the latter, methods were developed to identify protein complexes that are conserved across species (8,9). Other approaches for studying the evolution of protein pathways or complexes have been mostly based on sequence similarity only (10). Functionally linked proteins were shown to have a tendency to evolve together (11–13); conversely, proteins with similar phylogenetic profiles were shown to have higher chances of participating in the same biochemical pathways (14). Another study (15) showed that phylogenetic profiles of proteins in the same functional module tend to be significantly coherent, with variations in the level of coherence between different types of modules.

The evolution of modularity in PPI networks was studied by Pereira-Leal and coworkers (16,17), who proposed that the duplication of self-interacting proteins plays a key role in the formation of a modular network structure. Furthermore, they suggested that duplication of whole complexes is also a contributing factor for modularity, observing that a significant fraction of the complexes in Saccharomyces cerevisiae bare strong similarity to each other. An additional recent work (10) studied evolutionary cohesive modules in PPI networks, i.e. modules whose components have a uniform pattern of loss and gain throughout evolution. It was shown that younger cohesive modules play different roles than older ones and are more likely to be horizontally transferred. In addition, the cohesiveness of a module was shown to correlate with its size and inter-connectivity, and inversely correlate with the rate of duplication among the member proteins.

In this study, we present a novel computational framework for reconstructing the evolutionary history of protein complexes from a network perspective. Our method is based on generalizing established evolutionary measures for single proteins (18,19) to the level of protein subnetworks. Specifically, we define statistical measures for the level of homology between pairs of complexes, and use these measures to search for sets of orthologous complexes across species. The settings of our analysis differ from previous studies in three key points: (i) In contrast to previous studies (15–17) that restricted their analysis to known complexes and metabolic pathways, we consider a comprehensive set of computationally derived putative protein complexes in all of the studied species. (ii) We identify conserved protein complexes by taking into account both sequence and interaction patterns rather than testing conservation based on sequence only [as in (10)] or interaction only [as in (15)]. (iii) We consider all patterns of conservation rather than restricting the analysis to complexes that are conserved in all species [as in (8)].

We use the sets of orthologous complexes to infer evolutionary rate and age estimates for the member complexes. These estimates are validated in several ways and employed to investigate mechanistic aspects of protein complex evolution. We find a high level of agreement between the evolutionary rates of proteins and those of the complexes they form, supporting the view that protein complexes tend to undergo evolution as coherent units. Secondly, we study the role of duplication of self-interacting proteins in the evolution of protein complexes, showing that about one quarter of the sets of orthologous complexes are likely to have originated from conserved cores of homodimers that underwent duplication and divergence.

MATERIALS AND METHODS

PPI network construction

Our analysis includes seven species: Homo sapiens, Drosophila melanogaster, Plasmodium falciparum, Caenorhabditis elegans, budding yeast S. cerevisiae, Escherichia coli and Helicobacter pylori. For each species we obtained up-to-date PPIs and protein sequence data, gathered from recently published papers (20–29) and from public databases (3,30–36). High-throughput mass spectrometry data (22,27,28) was translated into binary PPIs using the spoke model (37). To deal with false positive errors (falsely reported interactions), we adapted a method by Bader et al. (38) and assigned confidence values to the interactions based on their supporting experimental evidence (Supplementary Data).

Protein cluster detection

We identify highly connected clusters within the PPI networks using two algorithms: (i) NetworkBLAST (8)—which performs a greedy search for dense subnetworks; and (ii) Markov clustering (MCL) (39)—which uses simulated random walks within the network to detect distinct clusters. The MCL method was recently shown to outperform other clustering techniques (40).

Protein clusters were obtained for each species separately by merging the outputs of the two algorithms, while maintaining an upper bound of 80% on the permitted overlap between clusters. The merging procedure as well as benchmarks of the two algorithms using the MIPS database are detailed in the Supplementary Data. The numbers of obtained clusters are depicted in Supplementary Figure 1a and range from 162 (P. falciparum) to 3419 (yeast).

To validate the collection of identified clusters, we measured the coherence of their member proteins with respect to their functional annotation and essentiality status. A total of 6854 (70%) of the clusters (across all species) exhibited significant functional coherence, and 1511 (34%) out of the 4366 clusters inferred for S. cerevisiae and E. coli (for which we had gene essentiality information) were significantly enriched with essential proteins (Supplementary Figure 2 and Supplementary Data).

As an additional validation, we evaluated the correspondence of the S. cerevisiae clusters to curated complexes from MIPS (41). This was done by computing sensitivity and specificity indices as in (42). Restricting the analysis to yeast clusters that intersect some MIPS complex, we found that 62% of those significantly match a known complex (sensitivity), covering 97% of the MIPS complexes (specificity; see Supplementary Data).

Constructing sets of orthologous clusters

The sets of orthologous cluster (SOC) construction consists of two steps: (i) identifying pairs of homologous clusters; and (ii) using the homologous pairs for identifying SOCs.

The homology relations are determined as follows: given two species α and β we define a protein similarity graph G = (V_α,V_β,E) where V_α (V_β) is the protein set of α (β). We connect pairs of sequence similar proteins by an edge, using a BLAST E-value cutoff of ≤10⁻⁶ (thus ensuring a significance level of approximately 0.01 after correcting for multiple hypothesis testing). Given two clusters c_α, c_β from species α and β, respectively, we measure their level of homology using two complementary statistical scores: (i) Edge-based score—the density of sequence similarity edges, connecting protein pairs from the two clusters:

where NE(A, B) is number of sequence similarity edges connecting pairs of proteins in sets A and B, and

is the hypergeometric score (43). (ii) Node-based score— the total number of proteins which have a potential ortholog on the opposite set:

where NV(A,B) is number of proteins in set B that are sequence similar to a protein from A.

We filter the computed relations by placing a bound of 5% on the false discovery rate (FDR) of the two scores (44) (i.e. in expectation, 5% of the discovered relations are false positives). Further requiring that for every related pair at least 25% of the proteins in one of the clusters have a sequence similar protein in the other cluster, yields a preliminary set of pairs of homologous clusters. For each cluster, we then report only its best match (taking the mean over the two scores) in each species and construct a cluster homology graph. The nodes in this graph correspond to protein clusters (across different species); and the edges connect clusters to their best matches (note that this relation might be one sided). Notably, the sequence similarity criterion employed in the protein similarity graph coincides with that of Sharan et al. (8) and Kelly et al. (45). We chose not to use stricter definitions such as reciprocal best BLAST matches, or members of the same Inparanoid (46) cluster, since as previously noted by Sharan et al. (8), this may result in missing many functional orthologs that exhibit a relatively weak sequence similarity signal.

The construction of the SOCs starts by enumerating all 7-node cliques (complete subgraph) in the cluster homology graph and then merging cliques that have six nodes in common until no more merging is possible. We then remove all the merged cliques from the graph and repeat the procedure using cliques of decreasing sizes. At iteration 1 ≤ i ≤ 6, the algorithm enumerates all the cliques of size 8 −i and merges cliques with 7 − i nodes in common. In the sixth and last iteration, we consider cliques comprised of pairs of clusters. To obtain a better support for the implied orthology relations within the SOCs resulting from these small seeds, we require the best-match relations between the two clusters in the clique to be mutual. We note that a SOC might contain a few clusters from the same species. These may be paralogous clusters or overlapping clusters.

Handling false negatives in the interaction data

False negative (undetected) interactions may lead to underestimation of conservation levels and result in discarding true orthology relations between clusters. To estimate the false negative rate in the data, we measured the fraction of potential cluster-orthology misses (Supplementary Data). Intuitively, we define a potential miss as a case where a cluster seems to be conserved when using only sequence data, and not conserved when using both sequence and PPI data. The estimated false negative rate for the entire data set was 40%.

To tackle this problem, we used a filtering criterion which aims at removing clusters for which orthologs may be obscured by lack of PPI data (Supplementary Data). The estimated false negative rate after the filtering was reduced to 36% (Supplementary Figure 3). The filtering reduced the size of the set of clusters that are members of a SOC by 25%. Notably, the set of species-specific clusters was reduced by 37.2% (Figure 2D). This pronounced difference indicates that many of the species-specific clusters may have been inferred as such due to lack of PPI data, and that our filtering procedure has managed to pin down many of those cases.

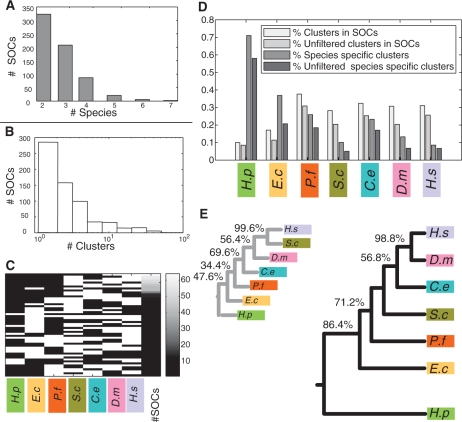
Figure 2.

Statistics on SOCs. (A) Number of species in the obtained SOCs. (B) Distribution of SOC sizes (number of clusters in SOC). (C) Phyletic patterns of SOCs. Each row represents an observed phyletic pattern, where white indicates presence and black indicates absence. The first seven columns to the left correspond to the different species. The eighth column depicts the frequency of the corresponding pattern, coded according to the color-bar on the right-most column. (D) Fractions of clusters participating in SOCs. Four bars are shown for each species (from left to right): fraction of clusters which are members of a SOC; fraction of clusters which are members of a SOC and pass the false negative filtering criterion (Supplementary Data); fraction of species-specific clusters; and fraction of species-specific clusters after filtering. (E) Phylogenetic trees relating the participating species. The larger tree (on the right) was reconstructed based on co-membership in SOCs. The tree on the left is based on conservation of single interactions. Percentages indicate the reproducibility of each branch in a bootstrap analysis (if different from 100%). Species names are abbreviated as follows: H. sapiens (H.s), D. melanogaster (D.m), C. elegans (C.e), S. cerevisiae (S.c), P. falciparum (P.f), E. coli (E.c) and H. pylori (H.p).

We also computed the false negative rate based on manually curated protein complexes from the MIPS database (Supplementary Data). The estimated rates (38.4% and 32.3% with and without filtering, respectively) are in line with the estimations above. Notably, the false negative rates computed for the prokaryotes (E. coli and H. pylori), along with that of P. falciparum, are substantially higher than those of the rest of the species in this study. In addition to the lack of experimental data in the latter two networks, this observed gap is likely to stem from actual differences in the networks themselves (namely, that sequence similarities are less likely to imply conservation of interactions) as evident from Figure 2E. While expected for the prokaryotes, it was also shown that wiring in the PPI network of P. falciparum is substantially different from that of other eukaryotes (47).

Propensity for gene loss and protein age estimation

The propensity for gene loss (PGL) (19) measure quantifies the conservation of a protein in evolution and is based on the presence/absence of its orthologs across a set of species (more details on the computational process are provided in the next section). To compute the PGL values, we obtained clusters of orthologous genes in 17 eukaryotic species from NCBI's HomoloGene database (48). The eukaryotic species include nine animals, five fungi, two plants and one pathogen. We considered the PGL values of all proteins whose ancestor dates back to the bilateria or fungi ancestors (or earlier) under an optimal parsimonious reconstruction. The corresponding phylogenetic tree was taken from NCBI and the divergence time estimates were taken from (49,50) (Supplementary Figure 5).

In addition, we classify the proteins into age groups according to the lowest common ancestor of their phyletic pattern in the phylogenetic tree. We treat the evolutionary age as a real value by representing every group by its estimated divergence time (Supplementary Figure 5). Species-specific proteins are assigned with a minimal age value of zero.

Propensity for cluster loss and cluster age estimation

A phylogenetic tree relating the investigated species was taken from NCBI (48). Divergence time estimates were taken from (49–52). In addition, we used an estimated divergence time of 2000 My between H. pylori and E. coli (Supplementary Figure 4).

The PCL measure is defined in an analogous manner to the protein-level PGL. Given a phylogenetic tree and a pattern of presence and absence of a protein cluster across the leaves of the tree, the pattern of presence and absence across all the inner (ancestral) nodes in the tree is determined using an optimal parsimonious reconstruction. This reconstruction seeks to minimize the number of losses along the branches of the phylogenetic tree, while being constrained by the Dollo parsimony principle, under which cluster loss is treated as irreversible [a cluster can be lost independently in several evolutionary lineages but cannot be regained (53)]. The PCL is then defined as the ratio between the total length of branches in the phylogenetic tree along which the cluster was lost and the total length of branches along which it could have been lost. For the computation of PCL, we considered only clusters that can be traced back to the eukaryotic ancestor or to the root of the phylogenetic tree under an optimal parsimonious reconstruction.

For age estimation, the clusters are classified into five distinct age groups: Bilateria, Fungi/Metazoa, Eukarya, Eukarya/Bacteria and species-specific. The assignment of a cluster to an age group is done according to the most recent ancestor, common to all the species in its phyletic pattern. Similarly to single proteins, we treat the evolutionary age of a cluster as a real-valued variable by representing every age group by its estimated divergence time (Supplementary Figure 4).

Gene duplication and cluster evolution

In the following, we consider two proteins of the same species as putatively paralogous if their BLAST E-value is lower than 10⁻⁶. For a given SOC, let S be its set of proteins, and let O denote the set of proteins from the participating species whose evolutionary age is not smaller than that of the SOC (as inferred by its phyletic pattern). We consider O∩S as the putative evolutionary core of the SOC. To evaluate the role played by duplication in the formation of a given SOC, we measure the enrichment of its core with duplicated, self-interacting proteins. To this end, we define P as the set of proteins that satisfy the following conditions: (i) the protein is self-interacting or has a self-interacting paralog; and (ii) it coresides in a cluster with one of its paralogs. We then compute a hypergeometric score quantifying the enrichment of the core with protein from P: HG(|O|,|O ∩ P|,|O ∩ S|,|O ∩ P ∩ S|). The obtained P-values were corrected for multiple hypothesis testing using the procedure of Benjamini and Hochberg (44) and placing an FDR cutoff of 5%, where the number of hypotheses equals the number of SOCs (647).

RESULTS

A framework for evolutionary analysis of protein complexes

We amassed PPI data from public databases and recent publications to construct a comprehensive up-to-date collection of PPI networks for seven species: H. sapiens, D. melanogaster, C. elegans, S. cerevisiae, P. falciparum, E. coli and H. pylori (Methods section, Supplementary Data.)

As experimental data on protein complexes are not available for most of the analyzed species (with the exception of S. cerevisiae, and to a lesser extent H. sapiens and E. coli), we applied computational approaches to infer protein complexes within each of the networks. To this end, we used two previously published algorithms for protein complex detection (8,39). We merged their results into a single collection of putative protein complexes, which we term clusters, for each network. Overall, we identified 9886 clusters within the seven networks (Supplementary Figure 1a). We validated the identified clusters by evaluating the coherency of their member proteins with respect to functional annotation and essentiality status (see Methods section). We used the identified protein clusters together with cross-species protein similarity information to derive SOCs, which are key to the evolutionary analysis presented in the sequel.

Sets of orthologous clusters

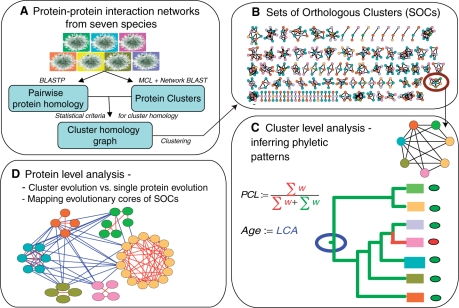
We define a SOCs as a collection of clusters from two or more species that are likely to have evolved from a common ancestral protein complex. To identify these sets, we extended the notion of a cluster of orthologous groups [COG, see (18)] from the single gene level to the level of protein subnetworks: the SOC inference algorithm starts by identifying pairs of clusters from different species that are potentially orthologous. The algorithm then proceeds to find sets of clusters (cliques), each from a different species, in which all members are potentially orthologous. Finally, the SOCs are formed using an iterative clustering procedure, which merges pairs of cliques that differ only by a single node. The SOC construction pipeline is depicted in Figure 1 and described in the Methods section.

Figure 1.

Overview of the SOC inference pipeline and subsequent analysis. (A) PPI networks of seven species are subject to cluster detection. (B) The obtained clusters are organized into orthologous groups based on sequence similarities of their member proteins. The subsequent analyses are done both on the cluster-level (frame C) and on the single protein-level (frame D). (C) The phyletic pattern of a given cluster is obtained according to the species present in the SOC it belongs to. Based on these patterns, we developed two novel measures for characterizing the evolution of clusters: PCL—an estimate for the rate at which the cluster was lost in evolution, and evolutionary age—the estimated emergence time of the cluster relative to the lineage split events in the phylogeny of the investigated species. The emergence time is estimated as the latest common ancestor (LCA) in the phylogenetic tree. (D) We study the correlation between the evolutionary properties of a cluster and those of its member proteins by comparing their evolutionary ages and loss rates. We also map the evolutionary cores of the SOCs to evaluate the role of gene duplication in their formation.

Altogether, we obtained 647 SOCs spanning two to seven species each, with a median of three clusters per SOC (Figure 2; see Supplementary Table 4 for the complete list of inferred SOCs). The SOCs allow inferring phyletic patterns for clusters (or whole SOCs), i.e. patterns of presence/absence of proteins clusters across the seven studied species. Overall, 52 out of the 120 possible phyletic patterns were observed, with the number of occurrences of each pattern varying from more than 50 (spanning different subsets of the investigated eukaryotes, excluding P. falciparum) to a single occurrence (typically involving both eukaryotes and prokaryotes). The SOCs cover 2823 (28%) of the clusters with relative ratios of coverage varying from 10% (H. pylori) to 37% (P. falciparum). Expectedly, the percentage of clusters participating in the SOCs was substantially lower for the two investigated prokaryotes due to their large evolutionary distance from the rest of the species.

To validate the computed SOCs, we first evaluated their functional coherence using the functional annotations of the participating clusters (Supplementary Data). 257 (39% versus a random expectation of 5%) of all SOCs and 219 (60%) of the SOCs of size three and more were found to be functionally coherent. In addition, we constructed a phylogenetic tree relating the analyzed species according to their co-membership in SOCs (Supplementary Data). The reconstructed tree (Figure 2E, right) highly matched the known tree of life (54) with the only exception being the lack of a separate prokaryotic clade. Notably, when using the conservation of individual PPIs rather than SOC co-membership to construct the phylogenetic tree, we obtained a less accurate tree with yeast and human placed together in a separate clade (Figure 2E, left). It is reasonable to assume that this deviation reflects the dominance of the yeast network in the available PPI data. Importantly, this effect vanishes when using cluster orthology as the basis for the tree reconstruction. As a further validation for the SOC construction, we traced the phyletic patterns of manually curated protein complexes from the MIPS database (41). We estimated the accuracy of these patterns by comparing the inferred presence/absence indicators to prior biological knowledge (Supplementary Data). The inferred patterns attained an accuracy level of 80%. Examples for SOCs constructed for MIPS complexes are given in Figure 3A and the Supplementary Data.

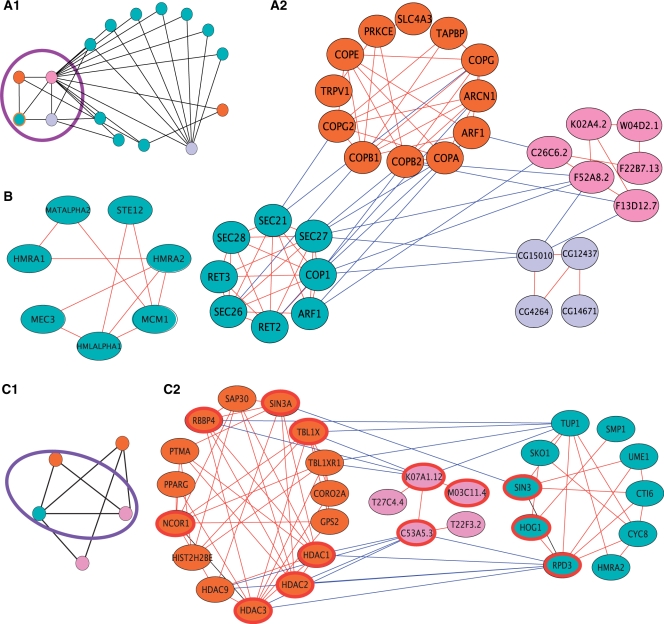
Figure 3.

Case studies of clusters and SOCs. (A) The manually curated COPI in yeast. A cluster-level view of the corresponding SOC is given in (a.1). In this view, each node represent a whole cluster and edges represent putative orthology relations between clusters. The nodes are color coded according to their respective species (as in Figure 2). The yeast COPI complex is highlighted by an orange frame and its immediate neighborhood is highlighted by a purple line. A protein-level view of the highlighted subgraph in (a.1) is given in (a.2). In the protein-level view, the nodes represent single proteins, and edges represent either homologies (between species, red edges) or PPI (within species, blue edges). (B) A yeast-specific mating-type determination cluster. (C) A chromatin modification SOC, whose evolutionary core is enriched with duplicated, self-interacting proteins. A cluster-level view of the SOC is shown in (c.1). A protein-level view of the highlighted subgraph in (c.1) is given in (c.2). The proteins composing the putative core of the SOC are highlighted by a red frame. Evidently, the homology relations between the participating clusters are based on two conserved sets of duplicated proteins that substantially cover the putative core. The upper set is comprised of a set of paralogs from human (TBL1XR1, TBL1X, RBBP4) and single representatives from yeast and worm (TUP1 and K07A1.12, respectively). Similarly, the lower set is comprised of a set of paralogs from human (HDAC1/2/3/9) and single representatives from yeast and worm (RPD3 and C53A5.3, respectively).

A notable problem in the analysis of large-scale PPI data in general and of protein clusters in particular, is the prevalence of false negatives. To tackle this problem, we restricted the analysis to clusters for which we had confidence in their inferred phyletic patterns, and filtered clusters for which orthologs in more than one species could not be detected due to possible lack of PPI data (see Methods section). The results presented in the following sections were obtained with the filtered collection of clusters.

Evolutionary measures for protein clusters

We developed two novel measures for characterizing the evolution of clusters: propensity for loss in evolution and evolutionary age. Both measures rely on the phyletic patterns induced by membership of a cluster in SOCs and on the phylogenetic tree relating the investigated species (Supplementary Figure 4).

The PCL is a cluster-level analog of the PGL measure introduced by Krylov et al. (19). The PGL of a gene is an estimate for the rate at which it was lost in evolution. Given a phylogenetic tree over a set of species and a phyletic pattern for the gene across these species, the PGL of the gene is the ratio between the overall lengths of branches along which the gene was lost and the total length of branches along which it was either lost or preserved. Analogously, we computed the PCL value of a cluster by reconstructing its phyletic pattern across the ancestral species in the phylogenetic tree that relates the seven investigated species, and measuring the relative length of branches along which the cluster was lost (see Methods section).

The evolutionary age estimate is based on a classification of the clusters into several distinct age groups reflecting their estimated emergence time relative to the lineage split events in the phylogeny of the investigated species. The age groups, in ascending order (from less to more ancient), include: Bilateria, Fungi/Metazoa, Eukarya and Eukarya/Bacteria. The age group of a cluster is determined as its latest possible emergence time under an optimal parsimonious reconstruction (see Methods section), in a manner similar to (10). We defined an additional age group, the species-specific group, as the set of clusters that have no putative orthologs in other species. We assign the clusters in this group with a minimal age value of zero. The distribution of species-specific clusters among the species shows a similar trend as before with higher rates of species-specific clusters found for the two prokaryotes, and covers a total of 15.8% of the clusters (Figure 2D). To validate the evolutionary measures, we investigate their correlation with various functional attributes. Our findings, provided in the Supplementary Data, are consistent with those previously reported for single proteins (18,19).

Mechanistic principles of protein complex evolution

The inferred phyletic patterns and evolutionary measures allow us to directly probe various mechanistic aspects of the evolution of protein complexes. In the following, we concentrate on two fundamental questions: do proteins tend to evolve independently of one another or do proteins within the same complex evolve in a coherent manner? And, how central is the role of gene duplication in the evolution of protein complexes?

Cluster evolution versus single protein evolution

The evolution of PPI networks was previously shown to have modular characteristics in the sense that proteins in a complex are likely to be lost or gained concomitantly (12–13). To obtain further insights into the evolution of complexes, we looked at the mode of organization of proteins into clusters throughout their evolution. We considered the following two trends: (i) the proteins in a cluster were originally unrelated and became a functional unit through evolution; and (ii) the organization into the same cluster characterizes proteins in a cluster ever since their emergence.

To test which of these scenarios is more prevalent, we computed the median PGL and evolutionary age values of the proteins in each cluster (see Methods section) and compared them with the respective PCL and cluster age values. We concentrated on the eukaryotic clusters, as PGL information for prokaryotic genes was not readily available. The results, summarized in Table 1, show significant correlations between the evolutionary attributes of a cluster and those of its member proteins. This supports the plausibility of the second scenario.

Table 1.

Correlations between cluster-level evolutionary measures and protein-level evolutionary measures

Evolutionary measure	Median PGL	Median protein age
Homo sapiens
Age	−0.270	0.364
PCL	ns	−0.243
Saccharomyces cerevisiae
Age	−0.339	0.438
PCL	0.201	−0.306
All
Age	−0.337	0.311
PCL	0.124	−0.240

Shown are Pearson correlation coefficients. Non significant correlations are marked as ‘ns’.

An example for a match between the conservation of complexes and proteins is the yeast coat protein complex I (COPI), which mediates intra-Golgi and Golgi-to-ER trafficking. The core proteins of the coat complex machineries are known to be highly conserved in eukaryotes (55). On the other hand, they are not expected to be present in prokaryotes, as they lack endomembranes (56). Consistent with this expectation, the SOC containing the COPI cluster in yeast is comprised solely of eukaryotic clusters, and includes all the investigated eukaryotes except P. falciparum (Figure 3A). Proteins comprising this SOC include both GTPases (ARF1 in yeast and human, F13D12.7, F52A8.2 and C26C6.2 in C. elegans, and CG15010 in D. melanogaster), and coat proteins (SEC21/27, COP1 in yeast and COPA, COPB1/2, COPG2 in human). Notably, interactions among coat proteins (and other proteins related to the COPI complex) are missing from the P. falciparum network; as a result, the corresponding cluster is missing from the set of P. falciparum clusters and, consequently, from the SOC containing the yeast COPI cluster.

A second example is the mating-type cluster in yeast shown in Figure 3B. This cluster contains the genes HMLALPHA1, MATALPHA2 and HMRA1, HMRA2 which are either expressed from the MAT locus by haploids or serve as silent cassettes for the exchange of mating types (57). In addition, it contains the Ste12 transcription factor and its interacting protein Mcm1. Being involved in a process which is highly specific such as mating, we would not expect this cluster to be evolutionary conserved. And indeed, the SOC construction identifies it as yeast-specific. On the other hand, when analyzing individual components of the cluster, we find that Mcm1 is highly conserved throughout the evolutionary scale. In addition to controlling mating functions, this protein also affects other processes in the cell such as cell-cycle progression, cell wall synthesis and DNA repair (58–60). Thus, despite the observed correlation, the evolutionary history of a complex does not necessarily reflect the evolutionary history of all of its components. This is probably due to the fact that individual proteins may find novel roles within the cell, not necessarily in the context of a complex.

The role of gene duplication in protein complex evolution

Gene duplication and subsequent divergence is one of the fundamental forces underlying the expansion of eukaryotic proteomes (61). It was recently hypothesized that it is key to the development of modularity in PPI networks as well (16). Specifically, it was suggested that a substantial portion of the complexes in the yeast PPI network have originated from evolutionary cores of homodimers. According to this hypothesis, those ancient homodimers served as ‘seeds’ which subsequently evolved to whole complexes through events of duplication, diversification and augmentation by additional proteins. To support this conjecture, Pereira-Leal et al. (16) derived a series of corollaries and showed that they hold in yeast. In particular, they showed that dimers of paralogous proteins are likely to have evolved from the duplication of homodimers, and that protein complexes tend to contain pairs of paralogs (see Supplementary Data for a validation of these corollaries on our data).

Here, we used the constructed SOCs to provide a more explicit validation for the role of duplication of self-interacting proteins in evolution. We hypothesized that a set of complexes that originated from an ancestor homodimer seed would contain a conserved core of paralogous, self-interacting proteins. To measure the effect of duplication of self-interacting proteins on the evolution of the clusters in our data set, we estimated how many of the SOCs conform with this expectation. For each SOC, we isolated its putative evolutionary core by considering only proteins whose estimated age is at least as high as that induced by the SOC (see Methods section). If the clusters in the SOC have evolved from duplications of a homodimer seed, we would expect the core to be enriched with paralogous self-interacting proteins. Hence, we computed for each SOC a statistical score that compares this level of over representation to random sets of proteins of at least the same evolutionary age as those contained in the SOC (see Methods section). After correcting for multiple hypothesis testing using the FDR procedure of Benjamini and Hochberg (44) and using a cutoff of 5%, we found that the cores of 142 (22%) of the SOCs were enriched with paralogous self-interacting proteins, clearly testifying to the important role of duplication in the evolution of protein complexes.

Figure 3C presents one such SOC. This SOC is annotated as chromatin modification and contains orthologous histone deacetylase units from H. sapiens, S. cerevisiae and C. elegans (panel 1). The putative core of the SOC, highlighted in panel 2, is dominated by two conserved sets of duplicated proteins. The first set comprises of a group of paralogs from human (TBL1XR1, TBL1X, RBBP4 associated with histone deacetylation and chromatin assembly) and a single representative from yeast and worm (histone-binding proteins TUP1 and K07A1.12, respectively), where the yeast representative is known to be self-interacting (62). The second set contains one representative from yeast and one from worm (the RPD3 and C53A5.3 histone deacetylase proteins), and four paralogous human proteins (HDAC1/2/3/9 belonging to the histone deacetylase family) in which two of the proteins (HDAC1/3) are self-interacting.

DISCUSSION

We presented a framework for evolutionary analysis of protein complexes. By generalizing concepts from the level of single proteins, we constructed orthologous sets containing clusters from seven different species. These sets allow us to infer patterns of presence and absence across the evolutionary tree, and consequently to estimate the propensity for loss in evolution and evolutionary age. We verified the orthologous sets in several ways including reconstructing the participating species' phylogeny and manually investigating a small set of hand-curated complexes.

We used the inferred SOCs to investigate mechanistic aspects of protein complex evolution. First, we probed the relationship between the evolutionary characteristics of a cluster as a whole and that of its constituents, observing a significant correlation between the two. Second, we have shown the importance of gene duplication as a mechanism for the evolution of protein complexes.

The resulting new evolutionary measures can be employed to study other aspects of protein complex evolution beyond the mechanistic aspects studied here. A fundamental question in this regard is how different functional attributes impact the evolution of a complex. In the Supplementary Data we show that the evolutionary rate of a complex significantly correlates with its level of connectivity in the network, the specificity of its function and its essentiality. These findings are consistent with those previously reported for single proteins (18,19) and agree with our previous findings on the coherent evolution of the protein members of a complex.

It is pleasing to see that current PPI networks are already rich enough to enable the careful study of intricate processes like protein complex evolution, after carefully controlling for the yet considerable rates of false positive and false negative interactions. But not less important, the integrated computational approach laid out here is likely to lead to many further new insights concerning protein complex evolution as molecular interaction databases continue to expand in their size, accuracy and species coverage.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Tel-Aviv University president and rector scholarship (to N.Y.); Israel Science Foundation and the Ministry of Science and Technology, Israel (to M.K.); A French-Israeli collaboration initiative funded by the Israeli Ministry of Science (MOST) (to E.R.); German Israel Foundation grant (to R.S.); Converging Technologies grant from the Israel Science Foundation (to M.K., E.R., and R.S.). Funding for open access charge: Israel Science Foundation.

Conflict of interest statement. None declared.