A Three-dimensional Statistical Reconstruction Model of Grapevine (Vitis vinifera) Simulating Canopy Structure Variability within and between Cultivar/Training System Pairs

Abstract

Background and Aims

In grapevine, canopy-structure-related variations in light interception and distribution affect productivity, yield and the quality of the harvested product. A simple statistical model for reconstructing three-dimensional (3D) canopy structures for various cultivar–training system (C × T) pairs has been implemented with special attention paid to balance the time required for model parameterization and accuracy of the representations from organ to stand scales. Such an approach particularly aims at overcoming the weak integration of interplant variability using the usual direct 3D measurement methods.

Model

This model is original in combining a turbid-medium-like envelope enclosing the volume occupied by vine shoots with the use of discrete geometric polygons representing leaves randomly located within this volume to represent plant structure. Reconstruction rules were adapted to capture the main determinants of grapevine shoot architecture and their variability. Using a simplified set of parameters, it was possible to describe (1) the 3D path of the main shoot, (2) the volume occupied by the foliage around this path and (3) the orientation of individual leaf surfaces. Model parameterization (estimation of the probability distribution for each parameter) was carried out for eight contrasting C × T pairs.

Key Results and Conclusions

The parameter values obtained in each situation were consistent with our knowledge of grapevine architecture. Quantitative assessments for the generated virtual scenes were carried out at the canopy and plant scales. Light interception efficiency and local variations of light transmittance within and between experimental plots were correctly simulated for all canopies studied. The approach predicted these key ecophysiological variables significantly more accurately than the classical complete digitization method with a limited number of plants. In addition, this model accurately reproduced the characteristics of a wide range of individual digitized plants. Simulated leaf area density and the distribution of light interception among leaves were consistent with measurements. However, at the level of individual organs, the model tended to underestimate light interception.

INTRODUCTION

Plant structure – the shape, location and orientation of the various components of the plant (Ross, 1981) – and optical properties control light interception and distribution within the canopy. Plant structure therefore influences a large number of physiological responses (e.g. stomatal aperture, photosynthetic activity, photomorphogenesis) and physical processes (e.g. organ temperature, controlling the kinetics of metabolic processes and the balance between these processes). In grapevine, as in most crop species, canopy-structure-related variations in light interception and distribution may affect productivity, yield (Smart et al., 1982; Morgan et al., 1985; Dry, 2000) and the quality of the harvested product (Kliewer and Lider, 1968; Kliewer, 1971; Reynolds and Wardle, 1989; Bureau et al., 2000; Bergqvist et al., 2001; Spayd et al., 2002; Downey et al., 2004). Both the intrinsic architectural traits of cultivars and canopy management practices (Smart et al., 1990; Gladstone and Dokoozlian, 2003; Willaume et al., 2004) affect canopy structure. Considerable attention has focused on canopy management systems in the last few decades (Shaulis et al., 1966; Carbonneau et al., 1981; Smart, 1985; Intrieri and Poni, 1995; Mabrouk and Sinoquet, 1998; Dry and Loveys, 1998; Dry et al., 2001; Gladstone and Dokoozlian, 2003). New training systems have been designed to enhance global light interception and distribution, and shoot vigour control has been improved by developing regulated deficit irrigation strategies. However, our ability to measure and/or to simulate large space-and-time variations in canopy structure and concomitant changes in microclimate is still a limit in evaluating the efficiency with which various canopy architectures harvest and distribute light (Schultz, 1995).

Many methods exist for simulating canopy structure. These methods differ principally in their level of description, ranging from a single variable indicating the mean leaf area density of the canopy to accurate descriptions of the size and position of each individual organ. Three general approaches are used. The simplest describes the plant canopy as one or several horizontally homogeneous layers of small particles (the ‘leaf gas’ or ‘turbid medium’ approach, Monsi and Saeki, 1953; Norman, 1982; Leuning et al., 1995). Spatial heterogeneity in many cultivated plant canopies (vineyards, orchards, open forests) has led several authors to propose a modification of this approach in which the turbid medium concept is applied within an envelope delimiting crown volume (Johnson and Lakso, 1991; Sinoquet et al., 1992; Law et al., 2001). Finally, the plant can be fully described through a set of discrete geometric primitives (cylinders, cones, polygons, etc.), the size and spatial organization of which depend on botanical rules (Prusinkiewicz, 1998; for a review see Birch et al., 2003) and/or direct measurements, such as three-dimensional (3D) digitization (Sinoquet and Rivet, 1997; Hanan and Room, 1997). Obviously, the time required for measurements increases with the amount of detail included in the representation. The choice of approach should therefore be considered carefully, bearing in mind the objectives of the study and the output variables.

Geometric approaches are increasingly used in structural–functional modelling, as they make it possible to compute plant functioning at scales ranging from individual organs to entire stands (Fournier and Andrieu, 1999; Yan et al., 2004; Allen et al., 2005; Chenu et al., 2005). However, when derived from simulation models, resulting architectures are seldom assessed by direct comparisons with real canopy structures. On the other hand, direct measurement methods result in the sampling of a very limited number of plants as soon as sufficiently large numbers of leaves have been produced (Sinoquet et al., 1998; Mabrouk et al., 1997a, b; Dauzat et al., 2001). In such cases, calculations for stands of plants are generally based on measurements from one to five plants, replicated to represent the field, and microclimatic variables are inferred from this sample, which is assumed to be representative. Although often ignored, plant to plant variability is probably significant in many cases (Casteran et al., 1980; Succi et al., 1997). This is particularly true for vine species, in which the shape of shoots is far from consistent (Carbonneau and Cargnello, 2003). In order to address this problem, this paper presents a statistical reconstruction model accounting for spatial variability in grapevine foliage in various cultivar/training system (C × T) pairs, at the plant and stand scales.

Several statistical models based on Monte Carlo simulation (Hammerley and Hanscomb, 1964) have been described (Succi et al., 1997; Ross and Ross, 1998; Giuliani et al., 2005). All these models infer the reconstruction rules for the canopy from an extracted data sample. Most represent the canopy according to the turbid medium concept, but a few recent studies have used the geometric approach, making it possible to determine light distribution at organ to canopy scales (Casella and Sinoquet, 2003; Sonohat et al., 2006). The approach generally used involves a minimal simplification of plant architecture and a reconstruction procedure based on the complete generation of plant topology (i.e. relationships of succession and connection between plant organs). These attempts have demonstrated the potential value of statistical reconstruction for accurately comparing the architecture of a few cultivars (two poplar clones, Casella and Sinoquet, 2003) or of a few training systems (three training systems of a given cultivar, Potel et al., 2005). However, a sizeable amount of work is still required for the characterization of new situations or the inclusion of additional measurement dates (e.g. simplified digitization requires recording of the point of origin for each 1-year-old shoot to be simulated). Furthermore, none of these models has been evaluated at both canopy scale (Casella and Sinoquet, 2003, based on hemispherical photographs of poplar stands) and organ scale (Giuliani et al., 2005; Sonohat et al., 2006, based on single digitized fruit trees). In the present study, we propose an original, simplified method combining the envelope-delimited turbid medium and geometric approaches, to represent large numbers of situations with tractable amounts of input data. This model has been adapted to grapevine, with the aim of capturing and mimicking the two main architectural traits involved in C × T pair phenotypic plasticity in this species: main shoot shape (Tomasi et al., 2005) and branch development (Lebon et al., 2004, 2006; Louarn et al., 2007).

The objectives of this study are thus (1) to propose a simple reconstruction model simulating individual shoot structure in order to represent canopy structure and its variability within and between grapevine C × T pairs, and (2) to assess quantitatively the accuracy of representations at the canopy, plant and organ level. Such a model involves a conceptualization of the plant architecture through a minimal set of rules common to all C × T pairs. A limited number of parameters were used to describe the variability of the 3D volume occupied by a shoot and we randomly distributed discrete leaf polygons within this volume, according to measured leaf area and branch distribution along the main shoot. The statistical reconstruction model was evaluated on eight contrasted C × T pairs by comparing, at the plot scale, simulated and measured light interception efficiency, and at the individual plant scale, the radiative balance of the leaves of simulated plants with that of the leaves of digitized plants.

MATERIALS AND METHODS

Plant material and vineyard layout

The study was performed from 2003 to 2004 in an experimental vineyard located in Chateauneuf de Gadagne (43·55°N, 4·56°E), Côtes du Rhône, France. Grapevines (Vitis vinifera L. ‘Grenache N’ (GRE) and ‘Syrah’ (SYR) on 110R rootstock) were planted in 1989, in 2·5 × 1·1-m rows orientated 90° from north. Four common spur-pruned canopy systems were studied for both cultivars: the Gobelet system (GOB), bilateral free cordon system (BFC), VSP-1W (bilateral cordons with one pair of catching wires), VSP-2W (bilateral cordons with two pairs of catching wires). These systems are outlined in Fig. 1. For all symbols and abbreviations see Table 1. Each plot consisted of four rows of 12 vines each. Measurements were limited to the 24 plants in the two central rows. The number of shoots was adjusted according to the vigour of the vine, with buds removed from each plant (stage 12, modified E.L. scale, Coombe, 1995) as a function of winter pruning weight. Bunches were thinned just after fruit set (stage 27 modified E.L. scale, Coombe, 1995), so that each shoot carried only one bunch of grapes.

Fig. 1.

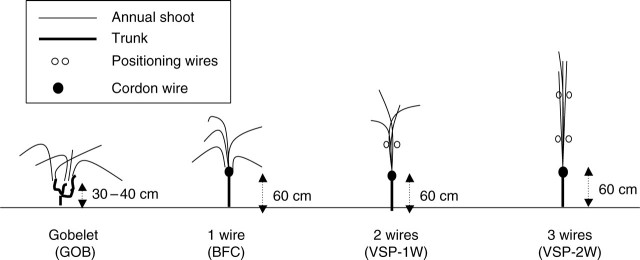
Schematic diagram of the four training systems studied (side view in the row direction).

Table 1.

Symbols and abbreviations

BFC	Bilateral free cordon system
VSP-1W	Bilateral cordons with one pair of catching wires
VSP-2W	Bilateral cordons with two pairs of catching wires
3D	Three-dimensional
a, b (a′, b′)	Slope and intercept of the linear relationship between primary (secondary) axis length and its number of phytomers
αl	Elevation of the vector normal to the leaf surface (°)
αs	Initial shoot elevation (°)
αs,i	Elevation of the ith internode (°)
B	Bias
C × T	Cultivar – training system pair
d (i, j)	Euclidian distance between i and j
ΔX, ΔY, ΔZ	Difference between the coordinates X, Y, Z of the two buds on a single spur (cm)
εint	Light interception efficiency. Two components are usually distinguished: the direct and diffuse components
f	Fraction of diffuse light in the global incoming light
ϕs	Angle between basal and distal tangents (°)
GOB	Gobelet training system
GRE	‘Grenache’
HP	Hemispherical photograph
ks	Kolmogorov–Smirnov test
LAD	Leaf area density (m2 m–3)
Lb	Length of the parallelogram used in the SOR definition
Lin	Internode length
Ls	Normalized length of the shoot
MXs	Proportion of shoot accounting for half of the curvature
n	Number of internodes on a shoot
nb	Number of measured shoots
nII	Number of phytomers on a branch
ωb	Angle of the parallelogram used in the SOR definition
RMSE	Root mean square error
SOR	Surface of revolution
sw	Shapiro–Wilks test
SYR	‘Syrah’
S	Variance–covariance matrix
θl	Azimuth of the vector normal to the leaf surface (°)
θs	Mean shoot azimuth (°)
VHI	Virtual hemispherical image
X0, Y0, Z0	Coordinates of the origin of the shoot
Xi, Yi, Zi	Basal coordinates of the ith internode
xl, yl, zl	Coordinates of the proximal point of the leaf lamina
x̄	Mean vector of shoot parameters
χ2	Chi-squares test

Model description

General presentation and organization

The 3D reconstruction model presented here combines a simplified method for describing the volume occupied by the shoot and random samplings for the positioning of individual shoot organs within this volume. It assumes that all shoots have identical leaf areas, the spatial distribution of which depends on the architectural characteristics of each C × T pair. Consequently, simulated shoot architectures theoretically have the same characteristics as a turbid medium circumscribed by the shoot envelope but, instead of an undefined number of infinitesimal leaves, the model generates a defined number of discrete leaves, determined as a function of mean shoot leaf area and mean individual leaf area. The canopy structure consists of several shoots partially occupying the same volume. The model was implemented in Python (http://www.python.org), using the PlantGL library for 3D visualization (ALEA platform, http://openalea.gforge.inria.fr/; Pradal et al., 2004) and the R statistical software for random sampling procedures (http://www.rpy.org).

This model requires two input files (Fig. 2), one describing the mean leaf area of the shoot, its distribution along the main axis and mean leaf size (mean shoot file), and the other describing plot layout and the number of shoots per plant (plot file). The output of the model is in the form of 3D virtual scenes. Given the stochastic nature of the model, it is possible to store the set of shoot parameters simulated during the reconstruction process in a temporary file (shoot parameter file) for reuse in subsequent simulations. Options are also available to visualize, in addition to the cloud of leaves simulated, shoot primary axes and trunks predefined for each pruning system.

Fig. 2.

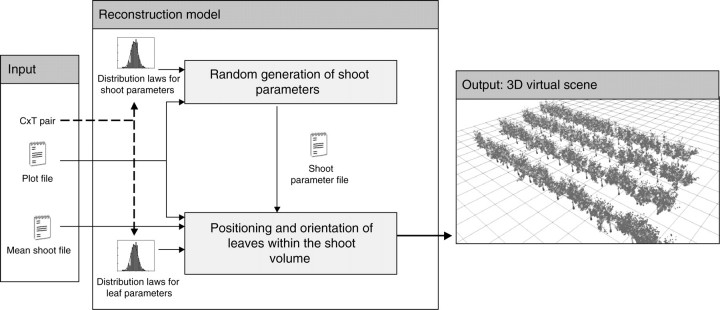
General overview of the model structure.

Shoot positioning

The origin of the shoot is defined by three parameters (X0, Y0, Z0), corresponding to the 3D coordinates of the position of the bud it originated from. For a given C × T pair, bud positions are imposed by both the pruning system and the genotype and were considered as independent of the trellising system. Two levels of organization can be distinguished. At the plot scale, vines are distributed in a single dimension along rows. At the individual vine scale, buds are located on regularly spaced spurs, the relative positioning of which depends on the pruning system. The model took these two levels of organization into account independently. Bud distribution at the plot level was specified according to plantation layout in the ‘plot file’ and the position of initial buds on individual vines was simulated stochastically for each vine of the plot, according to the following rules:

1. The first K buds of the vine are located on different spurs, K being the number of spurs in the pruning system considered. The X0_k, Y0_k, Z0_k coordinates of the kth bud were used to determine the univariate probability distribution for use within each of the K spurs.

2. Additional buds are then randomly attributed to the K previously located spurs for this plant. Their coordinates are defined relative to X0_k, Y0_k and Z0_k, using three univariate probability distributions DX, DY and DZ established for each genotype.

Spatial path of the primary axis

The volume occupied by the shoot is defined by the shape and size of the primary and secondary axes. A simplified set of five parameters was used to describe primary axes architecture (Fig. 3):

1. Mean shoot azimuth angle (θ_s)

2. Basal shoot elevation angle (α_s)

3. Difference between basal and distal tangent angle (ϕ_s), defined as the difference between basal and distal shoot elevation

4. Proportion of total shoot length accounting for half of the curvature (MX_s), defined as the ratio between the length from the origin of the shoot to the point of maximal curvature and the total length of the shoot

5. Normalized length (L_s), defined as the ratio between shoot length and mean shoot length for the C × T pair considered

Fig. 3.

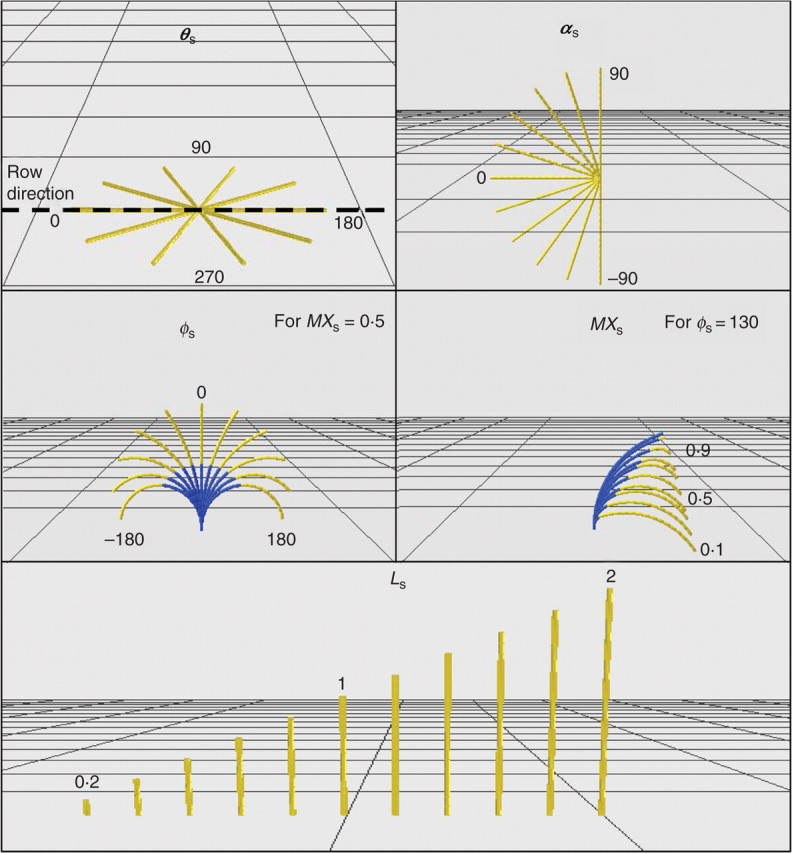
Impact on 3D path and range of variation of the five shoot parameters: mean azimuth θ_s, initial elevation α_s, angle between basal and distal tangents ϕ_s, proportion of shoot accounting for half of the curvature MX_s and normalised length L_s. The part shown in blue for ϕ_s and MX_s represent internodes before the point of maximal curvature.

Such a set of parameters enables us to approximate the spatial path of primary axes by drawing internodes as chords of two arcs of a circle, each accounting for half of the angular difference between the two extremities of the shoot. A primary axis of n phytomers thus follows a series of (X, Y, Z) coordinates:

1

where (X_i, Y_i, Z_i) are the basal coordinates and α_s,i the elevation of the ith internode and L_in internode length. For i = 1, α_s,i is equal to α_s and from i = 2 to n, α_s,i is calculated as:

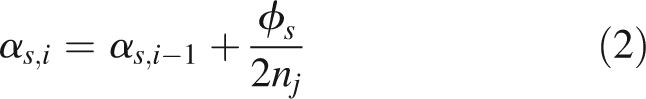2

where n_j is either n₁ = MX_sn when i is less than n₁ or n₂ = (n– n₁) when i is greater than n₁.

Internode length (L_in) is assumed to be constant for all internodes of a given shoot, and depends on two genotypic parameters a and b, linearly relating n to shoot length:

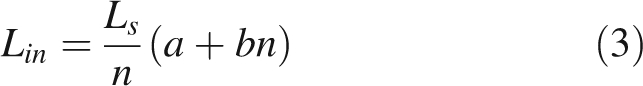3

This set of equations assumes that the path followed by the primary axis is included in a vertical plane defined by the point (X0, Y0, Z0) and the vector v⃗ (cosθ_s, sinθ_s, 0). This assumption seems to be realistic in the case of vine shoots trained without trellising as well as in widely used vertically trellised training systems where only one curvature point is observed in most of the shoots.

The five parameters used to describe the primary axis architecture are generated independently for each shoot and are also independent of the (X0, Y0, Z0) origin of the shoot. However, the five parameters of a given set are clearly not independent of each other. Indeed, at least some of these parameters are significantly correlated (e.g. shoot length and the angle between basal and distal tangents or shoot length and azimuth, because hedging practices result in the trimming off of shoots orientated towards the inter-row). In addition, the θ_s parameter displays a cyclical pattern characteristic of angular variables. The model overcomes these constraints by generating the shoot parameters as follows:

1. The θ_s parameter is first randomly selected from the [0°, 360°) interval, using a uniform probability distribution.

2. The other four parameters are then generated simultaneously, according to the azimuth sector in which the first sampling was made. Four azimuth sectors are distinguished: two corresponding to the row direction ([340°, 20°] and [160°, 200°]) and two to the inter-row direction ((20°, 160°) and (200°, 340°)). A multivariate normal probability distribution N_m (x̄,Σ) is associated with each of these azimuth sectors, x̄ being the mean vector of the parameters (α_s, ϕ_s, MX_s, L_s) and S the associated variance – covariance matrix.

3. Finally, the proportion of shoots in each azimuth sector is adjusted according to the observed data for each C × T pair.

Organ positioning and orientation

The model assumes that the 3D coordinates of leaf insertion points are uniformly distributed within a surface of revolution (SOR) defined by revolving a parallelogram P(L_in, L_b, ω_b) about each internode of the primary axis. For each primary internode, one primary leaf and n_II secondary leaves (taken from the mean shoot file) are positioned. L_b, the length of the second side of the parallelogram, is set to the mean length of a fully expanded petiole for the primary leaf and to the secondary axis length calculated as follows for the secondary leaves:

4

where a′ and b′ are two genotype-dependent parameters. The angle between adjacent sides of the parallelogram (ω_b) is set to 90° for the primary leaf (the volume enclosed in this SOR is therefore a cylinder of height L_in and of radius L_b) and to 45° for secondary leaves. Total shoot volume is determined by the union of the SOR used for the positioning of primary and secondary leaves at each node (Fig. 4).

Fig. 4.

Presentation of the three steps involved in the reconstruction process: (A) computation of the 3D paths of main shoots, (B) of the shoot volume and (C) location and orientation of individual leaves.

Finally, two additional parameters, θ_l and α_l, corresponding to the azimuth and elevation angles of the normal vector to the leaf surface, respectively, were used to define the orientation of leaves. As the probability distributions of these two parameters can be considered as independent (Sinoquet and Andrieu, 1993; Rapidel, 1995), univariate probability distributions were used. However, due to the strong anisotropy of row canopies, leaf azimuth cannot be assumed to be independent of the position of the leaf in the canopy (Mabrouk et al., 1997a). Two probability distributions, one for each side of the row, were therefore defined, and used according to the Y coordinate of the leaf insertion point.

Model parameterization

Probability distributions

Probability distributions for the ten architectural parameters used in the 3D reconstruction model were estimated for each of the eight studied C × T pairs. For eight of these parameters describing shoot architecture (i.e. X0, Y0, Z0, θ_s, α_s, ϕ_s, MX_s, L_s) estimates were made from measurements on a set of 200 shoots per C × T pair (20–24 vines) during the winters of 2003 and 2004. The spatial coordinates of three points per shoot (proximal, maximal curvature and distal points) were recorded, using an electrometric 3D digitizer (3Space Fastrak, Polhemus Inc., Colchester, VT, USA) and POL95 software (Adam and Sinoquet, 1995). The digitizer consists of a magnetic transmitter used as a reference frame and a pointer placed at the point to be recorded. The nominal device resolution is 8 × 10⁻⁴ m for an active volume of 1·2 × 1·2 × 0·8 m³ (Polhemus, 1993). The sole of the pointer was placed parallel to the internode, for the simultaneous recording of Euler angles, which under these precise conditions are rotation angles of the shoot at the measured point (azimuth, elevation and roll, hereafter referred to as azi_i, elv_i and roll_i). For each digitized shoot, a set of parameters was extracted, as follows:

5

6

7

8

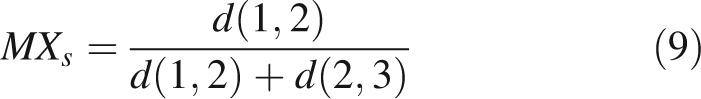9

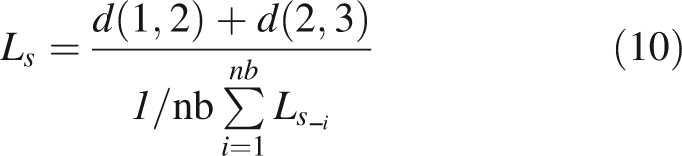10

where d (i, j) is the Euclidian distance between points i and j, nb is the number of measured shoots in the C × T pair concerned and L_s,i is the L_s parameter of the ith measured shoot. Mean vector and variance–covariance matrix of the multivariate normal probability distribution N_m (x̄ here, S) were then calculated as previously described (Krzanowsky, 2000):

11

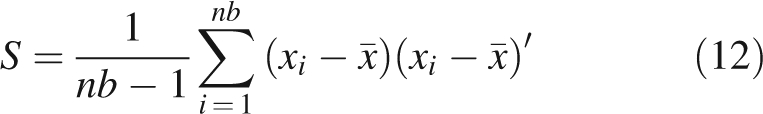12

where x_i is the vector representing the parameters of the ith measured shoot.

The relative position of the spur on the vine was also recorded, to establish specific distribution laws of the (X, Y, Z) coordinates for the various spurs of the pruning system. Finally, the relative positions of the shoot on the spur were recorded and probability distributions of ΔX, ΔY, ΔZ were calculated, using the initial shoot coordinates of both shoots located on a given spur.

The probability distributions of the parameters θ_l and α_l characterizing leaf orientation were estimated from measurements in July 2004 (stage 33, modified E.L. scale) on one fully digitized vine per C × T pair (representing a sample of 600–1000 leaves depending on the C × T pair). The proximal point (x_l, y_l, z_l) of each leaf lamina (i.e. the junction between petiole and lamina) was recorded with the sole of the pointer parallel to the leaf blade and with the pointer axis parallel to the leaf midrib. The calculation of θ_l and α_l from the recorded Euler angles was straightforward.

Allometric relationships

During the 2003 and 2004 growing seasons, leaves were counted and axes were measured weekly from budburst to setting on a sample of 60 primary shoots trained in VSP-1W per genotype. Similar measurements were made at mid-maturity (stage 36, modified E.L. scale, Coombe 1995) for all the secondary axes. These measurements enabled us to fit the allometric relationships presented in eqns (3) and (4). Allometric relationships are assumed to be independent of training system.

Assessment of the 3D statistical reconstruction model

The reconstruction model was evaluated at several levels, by comparing simulated virtual scenes with vineyard canopy structures characterized by means of hemispherical photographs (HPs) at the plot scale, or by comparing light interception properties and leaf area density (LAD) between digitized and simulated structures at the plant scale.

HPs are widely used for the characterization of plant canopy structure and for quantifying the radiation regime (Bonhomme and Chartier, 1972; Baret et al., 1993; Casella and Sinoquet, 2003; Cescatti and Zorer, 2003). In the present study, HPs taken during the 2004 growing season were compared with the corresponding virtual hemispherical images (VHIs) generated from model outputs. HPs were taken with a digital camera (Nikon Coolpix 950, Nikon, Melville, NY, USA) fitted with a fisheye lens with a 183° field of view (Nikon FC-E8 Fisheye Converter, Nikon) in uniform overcast sky conditions. The camera was put down on a horizontal 3-m movable steel bar, at a distance of at least 50 cm below the first canopy element. Twenty-four views were taken in four positions in the inter-row (six replicated transects between the two median rows; positions 1/4, 2/4, 3/4 and 4/4 in the inter-row for each transect) every 2 weeks or so (stages 23, 31 and 35, Coombe, 1995), in four contrasted experimental plots (BFC_SYR, VSP-2W_SYR, BFC_GRE, VSP-2W_GRE). On the same dates, mean shoot attributes (number of primary leaves, number of secondary leaves on branches, mean leaf area of primary and secondary leaves) were estimated from a sample of 15 shoots per C × T pair. Vine position and number of shoots per vine were recorded during the winter of 2004. These measurements made it possible to establish the ‘mean shoot’ and ‘plot’ files required by the model. VHIs corresponding to the real hemispherical photographs were generated from the simulated virtual scenes, using the POV-Ray™ ray tracing software (Persistence Of Vision™ Ray Tracer, version 3·5, http://www.povray.org), as described by Casella and Sinoquet (2003). HPs and VHIs were finally processed with GLA software (Gap Light Analyser version 2·0, SFU, Burnaby, British Columbia, Canada) and compared, based on direct (ε_int,direct) and diffuse (ε_int,diffuse) components of light interception efficiency (Fig. 5; Louarn et al., 2005):

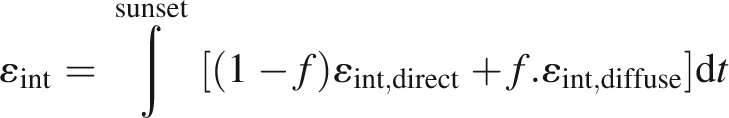13

where ε_int is light interception efficiency and f is the fraction of diffuse radiation in the global incoming light. Image processing consisted of three steps: (1) determination of the orientation of the image with respect to geographical north, (2) thresholding to discriminate the vine canopy from other elements and (3) radiative transfer calculation to estimate the transmitted fractions of direct and diffuse incoming light (Universal Overcast Sky, UOC model, Hutchinson et al., 1980). The latitude and longitude of experimental plots and the date of measurement were fed into the GLA radiative transfer model.

Fig. 5.

Examples of hemispherical pictures taken along a transect in the experimental plot of ‘Grenache’ plants trained in one-wire double-cordon system. (A–D) Photographs taken in position 1/4, 2/4, 3/4 and 4/4, respectively, in the inter-row. The yellow line indicates the sun track on 15 July.

Two series of simulations were carried out before VHI generation and processing, to evaluate the consequences of the various stages in the reconstruction process (i.e. definition of shoot volume and random positioning of leaves within the defined volume) at plot scale. A first set of simulations (subscript ‘pf’ for ‘partially fixed’) was generated using a ‘shoot parameter’ file directly deduced from shoot digitization during the winter of 2004 (i.e. the shoot parameters of the two median rows were those estimated from the corresponding shoots in the vineyard; only leaf positioning was generated by the model). A second set of simulations (subscript ‘fr’ for ‘free’) was obtained using all the probability distributions parameterized for each C × T pair.

Finally, our comparison between statistical reconstructions and precise descriptions of a few plants was completed by generating VHIs (subscript ‘dig’) from a virtual vineyard of a single digitized plant duplicated 48 times so as to give a planting density identical to that of the plot for the same C × T pairs as the VHI_fr.

At the plant scale, 3D mock-ups of digitized vines were compared with model simulations of the corresponding vines, using the directly measured ‘mean shoot’ and ‘shoot parameter’ files. Ten replicates of the simulated mock-ups were generated to assess the variability in canopy structure resulting from the random sampling of leaf position and orientation. LAD distribution was first compared between simulated and digitized situations. Radiative balance was then computed at the organ scale, on both types of mock-up, using the ARCHIMED software available on the ALEA platform (Dauzat and Eroy, 1997). The distribution of daily cumulative global light intercepted by leaves was determined for both types of mock-up.

Statistical analysis

Shapiro–Wilks' (sw) and one-sample Kolmogorov–Smirnov (ks) tests were used to assess the normality of univariate distributions. The null hypothesis of normality was rejected if both tests were significant. The two-sample Kolmogorov–Smirnov test was used for the pairwise comparison of parameter distributions. Analysis of covariance (ANCOVA) was used to compare the different linear allometric relationships obtained.

Simulated and measured light interception efficiencies were compared using the root mean square error (RMSE) and bias (B) of the model, calculated as follows:

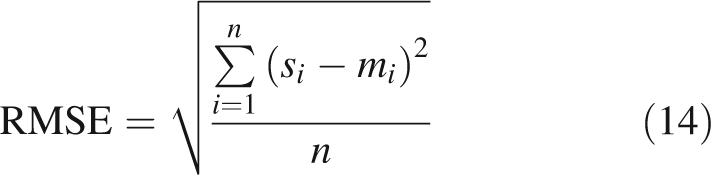14

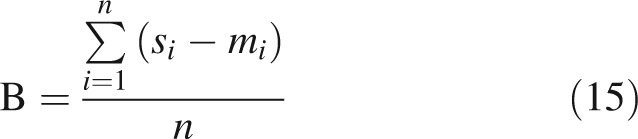15

where s_i and m_i are the ith simulated and measured values, respectively, and n is the number of observations.

Finally, the homogeneity of the distributions of LAD and cumulative global light interception by leaves was assessed with the chi-squared (χ²) test, taking the digitized data distribution as the theoretical one.

RESULTS

Model parameterization for different C × T pairs

Step 1: Origin of the shoot

The distributions of the three parameters (X0, Y0, Z0) defining the origin of the shoot are presented in Fig. 6. At the spur scale, all distributions were normal (sw, P > 0·4). Significant differences between spurs were found only for X0_i of the double cordon and for X0_i and Y0_i of the gobelet (ks and sw, P < 0·001) systems. No differences were observed for Z0_i (P > 0·31). When significantly different, the distributions often overlapped considerably, leading to complex but predictable patterns of probability density at the plant scale for the two pruning systems. Shoots from vines pruned in double cordons had a Z0 coordinate 0·20 m higher than that of vines in the gobelet system. Consistent with the pruning rules followed by vine growers, the combination of X0 and Y0 parameters defining the relative position of the spurs showed that shoots were regularly spaced along the row in the double cordon system. By contrast, hot spots of shoot density probability around the trunk were observed in the gobelet system.

Fig. 6.

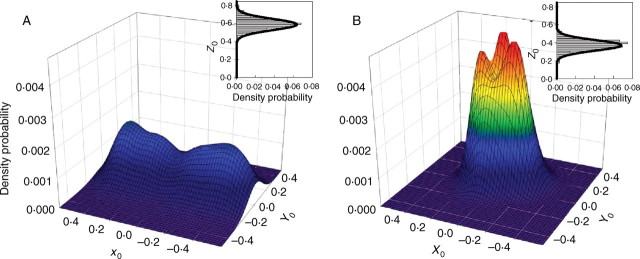
Probability density functions of the three parameters (X0, Y0, Z0) characterizing spur (lower shoot bud) position for training systems pruned in the double-cordon (A) and gobelet (B) systems.

Finally, the three probability distributions ΔX, ΔY, ΔZ enabling the relative positioning of shoots on a given spur also followed normal distributions [N (−0·2, 2·3), N (0·1, 1·9), N (1·7, 1·1), respectively, n = 290, sw, P > 0·12). No significant differences were found between genotypes or between pruning systems (ks, P > 0·2).

Step 2: Shoot parameters

All the univariate distributions of shoot parameters, except for mean azimuth θ_s (ks and sw, P < 0·001), were normal (P > 0·08). It was therefore possible to calculate the mean vector x̄ and variance–covariance matrix S of the multivariate normal distribution for each of the C × T pairs studied. Table 2 illustrates the results by presenting the estimated x̄ in the most representative azimuth sector (>45 % of the shoots). For both genotypes, there was a significant gradient from non-trellised C × T pairs (GOB, BFC) to lightly trellised (VSP-1W) and heavily trellised C × T pairs (VSP-2W). Trellising tended to increase the mean values of the α_s, ϕ_s and MX_s parameters. Trellised shoots were therefore more vertical, and natural bending, characterized by MX_s values below 0·45, was modified by the wires (MX_s > 0·5). The two cultivars differed principally in terms of their angle between basal and distal tangent values ϕ_s. This parameter remained almost constant regardless of the training system in ‘Grenache’ but was highly sensitive to trellising in ‘Syrah’ shoots. This later displayed larger average values for trellised systems than for the BFC or GOB systems. Mean vectors also differed between azimuth sectors in some cases, particularly for trellised C × T pairs (data not shown). θ_s had a marked effect on L_s (i.e. shoots were longer in the direction of the row) and α_s (i.e. smaller initial elevation in the direction of the row). Correlations between the different parameters of a given vector are also given in Table 2. The variance–covariance matrix varied greatly from one C × T combination to another. For instance, significant correlations were found between α_s and ϕ_s for the four trellised C × T pairs but were not systematically found in the other combinations. Conversely, α_s and L_s were clearly linked in most of the non-trellised C × T pairs, but were never linked in the VSP-1W or VSP-2W training systems. The correlation between L_s and ϕ_s was the strongest and most widespread. These multiple correlations moreover confirmed that random drawings in a series of independent univariate distributions would be inappropriate to represent grapevine shoot architecture.

Table 2.

Mean vector x̄ and normalized variance–covariance matrix S characterizing the multivariate normal distribution of shoot parameters (α_s, ϕ_s, MX_s, L_s) for the eight studied C × T pairs. Examples are taken from the azimuth sector facing south [(200°, 340°)]

		‘Syrah’					‘Grenache’
			S					S
		x̄	αs	ϕs	Ls	MXs	x̄	αs	αs	Ls	MXs
GOB	αs	25·43	1·00	−0·09	−0·16	0·18	41·89	1·00	−0·60	0·08	−0·30
	ϕs	−42·10	−0·09	1·00	−0·33	0·11	−23·28	−0·60	1·00	−0·39	0·16
	Ls	1·05	−0·16	−0·33	1·00	−0·20	1·11	0·08	−0·39	1·00	−0·02
	MXs	0·41	0·18	0·11	−0·20	1·00	0·43	−0·30	0·16	−0·02	1·00
BFC	αs	22·65	1·00	−0·10	−0·36	0·18	46·27	1·00	0·08	0·38	0·07
	ϕs	−44·06	−0·10	1·00	−0·43	0·13	−10·84	0·08	1·00	0·15	0·01
	LEN	1·04	−0·36	−0·43	1·00	−0·20	1·04	0·38	0·15	1·00	−0·06
	MXs	0·41	0·18	0·13	−0·20	1·00	0·45	0·07	0·01	−0·06	1·00
VSP-1W	αs	60·64	1·00	−0·39	0·14	−0·14	58·04	1·00	−0·38	0·07	0·01
	ϕs	−62·66	−0·39	1·00	−0·46	0·12	−30·18	−0·38	1·00	−0·59	0·09
	Ls	0·92	0·14	−0·46	1·00	−0·17	1·05	0·07	−0·59	1·00	−0·14
	MXs	0·54	−0·14	0·12	−0·17	1·00	0·62	0·01	0·09	−0·14	1·00
VSP-2W	αs	73·79	1·00	−0·23	−0·14	0·19	74·06	1·00	−0·35	−0·01	0·14
	ϕs	−56·40	−0·23	1·00	−0·63	0·00	−28·26	−0·35	1·00	−0·45	−0·20
	Ls	1·03	−0·14	−0·63	1·00	−0·09	1·03	−0·01	−0·45	1·00	0·06
	MXs	0·60	0·19	0·00	−0·09	1·00	0·62	0·14	−0·20	0·06	1·00

The parameters of the empirical allometric relationships between the number of phytomers and axis length obtained for both genotypes are given in Table 3. Significant differences were observed for the primary axis, with ‘Syrah’ systematically presenting longer shoots than ‘Grenache’ (F = 157, P < 0·001). Secondary axes were shorter for a given number of phytomers but no genotypic differences were observed (F = 1·48, P = 0·34).

Table 3.

Parameters of allometric relationships (eqns 3 and 4) for ‘Grenache’ and ‘Syrah’

		‘Grenache’	‘Syrah’
Primary axis	a	65	88·4
	b	–243·8	–394
	r2	0·96	0·95
	CV	0·1	0·1
Secondary axis	a′	43·2	38·6
	b′	−72·9	−52·4
	r2	0·9	0·89
	CV	0·22	0·32

Step 3: Leaf parameters

Table 4 presents the estimated distributions of the leaf parameters θ_l and α_l associated with the various C × T pairs. All the observed distributions of α_l were normal (n > 650, sw, P > 0·55). For both genotypes, α_l was lower (i.e. leaf elevation was greater) in trellised training systems than in non-trellised systems (ks, P < 0·001). For θ_l, all but the BFC distributions displayed a typical Gaussian shape for each side of the row, with mean azimuth reached at ± 90° to the row direction, depending on the side (n > 650, sw, P > 0·14). In the BFC system, the observed distributions appeared to be uniform. These results thus confirmed that rows have a strong impact on leaf orientation if the shoots are positioned, but not if the shoots were allowed to orientate themselves freely.

Table 4.

Mean and standard deviation (in parentheses) characterizing the leaf parameter distributions (θ_l, α_l) of the eight studied C × T pairs

	GOB		BFC		VSP-1W		VSP-2W
	‘Grenache’	‘Syrah’	‘Grenache’	‘Syrah’	‘Grenache’	‘Syrah’	‘Grenache	‘Syrah’
αl	41·7 (19·3)	50·2 (19·4)	40·6 (19·0)	49·9 (17·4)	36·5 (17·3)	44·4 (20·1)	33·3 (19·7)	41·6 (21·2)
θl (north side)	83·2 (88·0)	89·1 (81·1)	82·4 (107·8)	98·8 (92·5)	91·2 (70·9)	87·2 (82·7)	80·6 (56·3)	90·1 (50·7)
θl (south side)	277·5 (92·9)	283·9 (100·9)	277·0 (115·6)	270·8 (107·4)	275·7 (71·9)	271·3 (75·3)	271·6 (91·2)	277·2 (68·4)

Assessment of the reconstruction model at the canopy scale

A first step in the process of evaluation of the reconstruction model was performed at the canopy scale, by comparing the light interception efficiency values (ε_i) measured during the growing season of 2004 with those estimated from the virtual scenes obtained as outputs of the model (Fig. 7).

Fig. 7.

Comparison of photographs taken in a real vineyard (veraison, stage 35, Coombe, 1995) with the corresponding simulations for one-wire (BFC) and three-wire (VSP-2W) training systems.

Figure 8 presents the daily integrated ε_i measured along an inter-row transect for four contrasting C × T pairs at veraison (end of vegetative growth usually observed in vineyards, stage 35 of the modified E.L. scale, Coombe 1995). The results show that the sampled HPs covered a wide range of ε_i values (20–67 % for this last measurement date alone). Both components of ε_i had similar spatial patterns, whatever the C × T pair considered. A minimal value was systematically observed in the middle of the inter-row (position 3), with the maximal value obtained near the row (position 1 or 2). These patterns were characteristic of the C × T pairs in all cases, except between the two VSP-2W systems. For a given position, variability in ε_i,direct (1–16 %) was greater than variability in ε_i,diffuse (0–6 %). Indeed, ε_i,diffuse integrates the whole sky vault seen from the digital camera location whereas ε_i,direct focuses on the canopy structure along the track followed by the sun (Fig. 5). As a result of the orientation of rows in this experiment, ε_i,direct was strongly affected by the variability between plants in the row. This variability was lower for ε_i,diffuse because it was weighted by large open-sky solid angles due to inter-rows.

Fig. 8.

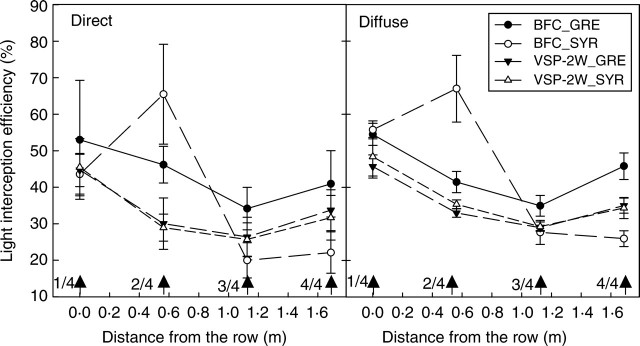
Measured spatial distribution of light interception efficiency for the direct and diffuse components of incoming light in the one-wire (BFC) and three-wire (VSP-2W) training systems. Arrows indicate positions 1/4, 2/4, 3/4 and 4/4 in the inter-row.

Figure 9 gives a comparison of ε_i components calculated from HPs in the vineyard with those calculated from VHIs generated from model outputs. Two rounds of simulation were carried out. In the first (Fig. 9A, B), the model was partially fixed (i.e. shoot parameters were imposed from direct measurement in the field) to minimize the impact of stochastic procedures on canopy structure. The light interception efficiency values calculated from VHI_pf were consistent with field data in terms of both absolute values (RMSE < 5·0 %; |B| < 2·9 %) and in the reproduction of variability (pairwise t-test on the confidence intervals, P > 0·26). Simulation accuracy was also shown to be similar for the various C × T pairs studied (RMSE < 5·3 %; |B| < 3·5 %). A second round of simulation was carried out, using a stochastic procedure generating vectors of shoot architecture parameters (Fig. 9C, D). As in previous simulations, ε_i,direct and ε_i,diffuse calculated from VHI_fr were both highly consistent with field data in absolute values for all the measurement dates and all C × T pairs (RMSE < 4·6 %; |B| < 1·8 %). The variability between VHIs was also correctly simulated (pairwise t-test, P > 0·72).

Fig. 9.

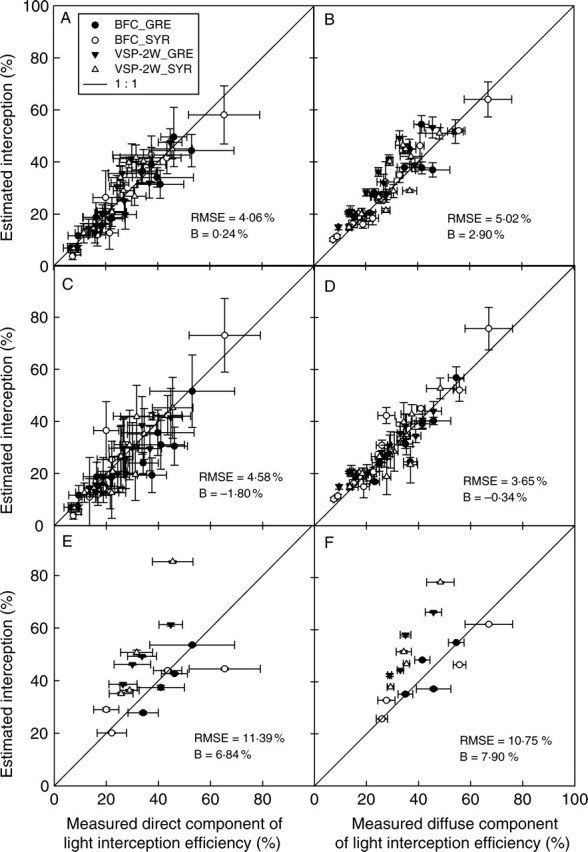
Comparison of measured and simulated light interception efficiency estimated from virtual scenes for the direct (A, C, E) and diffuse (B, D, F) components of incoming light. A, B and C, D correspond to partially fixed and free stochastic simulations, respectively; E, F represent virtual scenes obtained by the duplication of a single fully digitized plant. RMSE: root mean square error; B: bias.

Finally, ε_i values measured in the vineyard were compared with those calculated from virtual scenes consisting of one digitized vine duplicated 48 times, in line with the planting scheme of each plot (Fig. 9E, F). Even if a strong correlation was found between measured and simulated ε_i, RMSE values were significantly higher (11·4 and 10·8 % for ε_i,direct and ε_i,diffuse, respectively) than for ε_i calculated from the output of the model (<5·5 % for the same measurement date). Indeed, this method of representing canopy structure does not take into account plant to plant variability and thus heavily weights the single sampled plant. Depending on how representative the plant concerned turns out to be, this may result in satisfactory representations (e.g. BFC_GRE) or highly biased representations (overestimation in the case of VSP-2W_SYR, underestimation in the case of BFC_SYR, |B| > 5 %).

Assessment of the reconstruction model at the plant scale

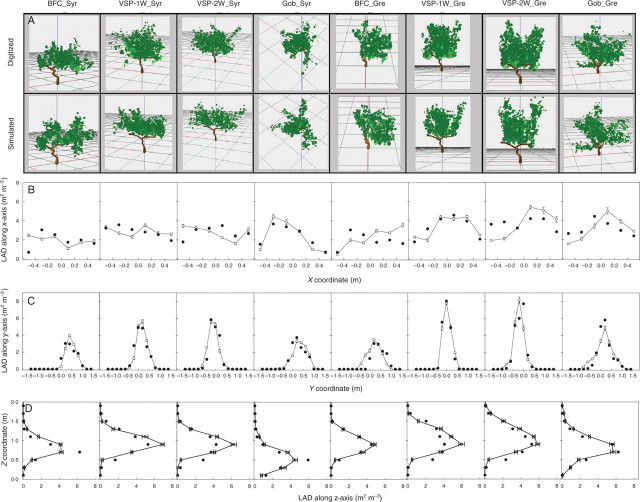
Model accuracy was assessed further, at the single plant scale. Visual comparisons of eight digitized plants representing the various C × T pairs studied with the corresponding simulated plants revealed good agreement between the exhaustive architecture measurements and the various simulation runs (Fig. 10). Slight discrepancies were visible in the general shape of some ‘Syrah’ shoots and the volumes they occupied (GOB_SYR, VSP-1W_SYR, Fig. 10A). These discrepancies seemed to result primarily from an oversimplification of the 3D path of the primary axis concerned for the set of five shoot parameters. Slight overestimations of canopy porosity in simulated mock-ups were also observed in some vines (VSP-2W_SYR, VSP-2W_GRE). Such overestimations were observed only for plants of well-trellised C × T pairs carrying large leaf areas. This may indicate that, in cases of high leaf area density, the assumption of independence of leaf orientation between the different leaves of the canopy does not hold.

Fig. 10.

Leaf area density distribution along the x- (B), y- (C) and z- axis (D) of the space for one fully digitized vine per C × T pair (solid circles) (A) and its corresponding simulation (open circles). Bars indicated confidence intervals on ten replicates of the simulated virtual scene at P = 0·05.

In order to quantify the visual impression of good agreement between the canopy structures of both types of mock-up, spatial leaf area density distributions were compared for each of the eight situations (Fig. 10B–D). The results show that a wide range of canopy structures was represented in this sample of plants: the maximal vertical LAD was between 4·2 m²m⁻³ (BFC_SYR) and 6·7 m²m⁻³ (VSP-2W_SYR), reflecting major differences in distribution shapes and canopy heights. Simulated LAD distributions satisfactorily fitted the measured values extracted from digitized data along the most-discriminating y-axis for the whole range of situations tested (χ² < 7·9, P > 0·16). However, significant differences were observed for the x-axis (BFC_SYR, BFC_GRE, VSP-2W_GRE, χ² > 11·7, P < 0·04) and z- axis (BFC_SYR, VSP-2W_SYR, VSP-1W_GRE, χ² > 12·8, P < 0·03) for some training systems. The inter-run variability of LAD was low for a given situation (confidence interval < 0·3 m²m⁻³; P = 0·05, n = 10), suggesting that the random positioning of leaves within the shoot volume occupied has little effect on LAD distribution.

Finally, the ability of the partially fixed reconstruction procedure to reproduce the light environment experienced by leaves was evaluated. In digitizations of ‘Grenache’, the distribution of leaf area in classes of daily cumulative intercepted radiation showed two clearly different patterns, depending on the training system (Fig. 11). Trellised vines (VSP-1W, VSP-2W) presented significantly different distributions (χ² > 26, P < 0·001), with a higher proportion of leaves in the most shadowed class, than non-trellised vines (BFC, GOB). In digitizations of ‘Syrah’, by contrast, these distributions were similar for all sampled plants (χ² < 2·4, P > 0·8). Model outputs were consistent with these results and reproduced the distributions for all C × T pairs (χ² < 8·5, P > 0·3). The simulated proportion of leaves in the most shadowed classes was, however, slightly overestimated, leading to the almost systematic over-representation of classes with intercepted light levels below 100 W m⁻² (up to 0·4 m²for VSP-2W_GRE, Fig. 11).

Fig. 11.

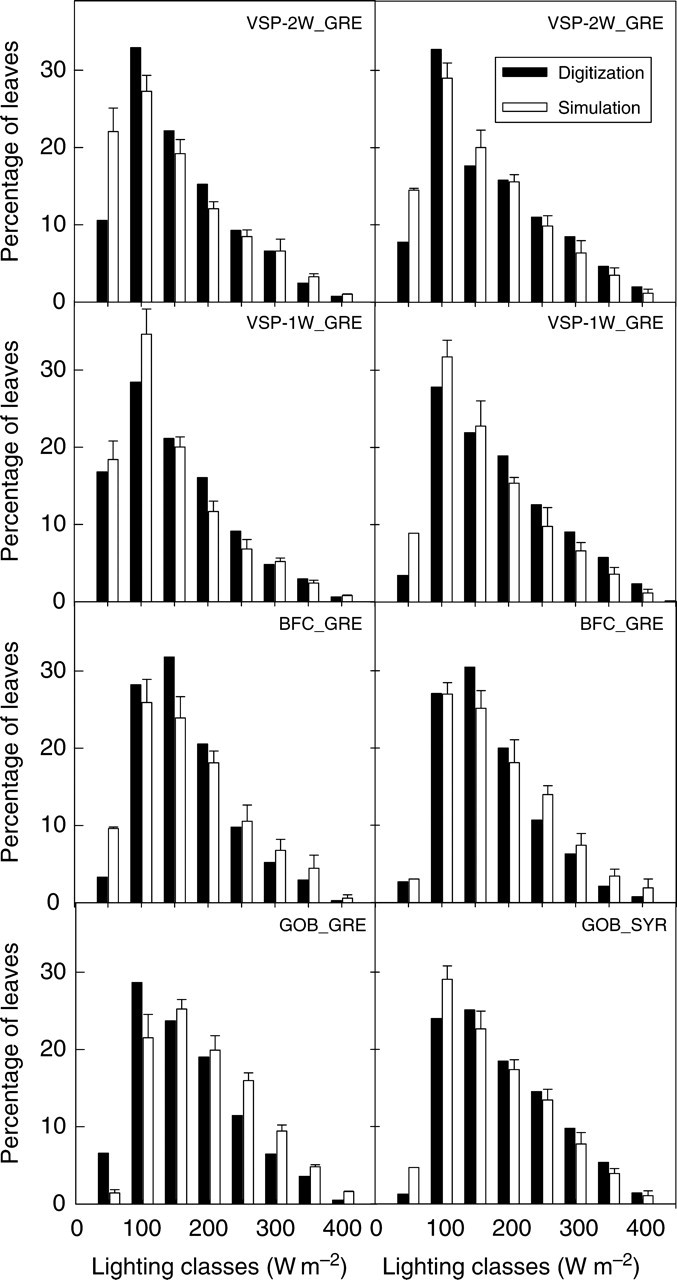
Distribution of cumulative daily intercepted radiation for one fully digitized vine per C × T pair and its corresponding simulation.

DISCUSSION

The aims of this study were to describe and evaluate a statistical reconstruction model simulating grapevine canopy structure and its variability, to compare different C × T pairs on the basis of relevant ecophysiological variables, such as light interception efficiency (ε_int) at the stand scale (involved in carbon acquisition, Monteith, 1977; Smart et al., 1982) or the distribution of light interception at the organ scale (involved in fruit ripening and quality development, Spayd et al., 2002). The model relies on two levels of simplification. First, the canopy is seen as an aggregation of homogeneous herbaceous shoots, the leaf area of which can be approximated by a ‘mean shoot leaf area’. Then, architecture variability between individual shoots is assumed to be primarily due to the variability in primary axes spatial paths for a given date (Tomasi et al., 2005), and secondarily due to differences in the volume occupied by the branches between different dates or plots. Based on these assumptions, the proposed reconstruction process focuses on computation of the 3D path of the primary axis and on the definition of a volume surrounding this path in which leaves are randomly distributed. It makes it possible to consider variations in shoot leaf area or occupied shoot volume, but this is currently possible only through a ‘mean shoot’ definition supplied as an input. Model parameterization thus focuses on the most discriminating geometric traits and ignores both topology and the geometric traits of the many branches, which are simply replaced by a ‘cloud of leaves’ concept. This pragmatic simplification represents a significant departure from generic methods of describing plant architecture, combining geometry and topology from data acquisition (Godin et al., 1999). However, this should not be seen as a step backwards. Instead, it reflects the need to adapt the conceptualization of complex canopies such as that of a vineyard and to concentrate data acquisition on the architectural determinants of light interception. This simplified procedure is indeed highly consistent with our knowledge of grapevine botany and physiology. For instance, breaking down shoot volume into a sum of flexible SOR allows the location of a correct number of leaves in a realistic prospected volume originating at each primary node, making it possible to take into account the great variability of branch development due to primary shoot structure (Ordovas et al., 1983), genotype (Louarn et al., 2007) or the environment (e.g. temperature, soil water deficit, Lebon et al., 2004, 2006). On the other hand, the most stable traits, such as leaf size or the topological relationship between axes (Lebon et al., 2006), are assumed to be fixed.

The approach reported here differs from previous statistical reconstruction models (Whitehead et al., 1990; Ross and Ross, 1998; Giuliani et al., 2005) in two main ways. First, it simulates complex canopy structure interactions between environment-related plasticity of the shoot, cultivar and training system from a very limited number of parameters, thereby maximizing the number of situations that can be studied. Second, this model was designed to allow the construction of virtual plants having insight at scales varying from the canopy to the shoot instead of focusing on either canopy (Casella and Sinoquet, 2003) or single plant (Giuliani et al., 2005) representations.

All the defined parameters displayed a significant variability within the range of canopy structure characterized and appeared to be relevant. Indeed, even if some of the shoot parameters were significantly correlated (Table 2), no systematic correlation across the various C × T pairs was observed, indicating that each parameter contributed to the description of the variability. We are also of the view that simplifying parameterization should not simply involve limiting the number of parameters through an appropriate conceptualization of architecture, but should also involve identifying parameter distributions common to different C × T pairs or reusable on different dates for a given situation. As parameter distributions are obtained from field measurements, they must be reset for each new date (Whitehead et al., 1990; Casella and Sinoquet, 2003). However, several of the defined parameters have seemingly constant distributions in grapevines, at least for a range of conditions. This is the case for shoot parameters between flowering and harvest, a period representing most of the growing cycle and during which primary axes maintain approximately the same shape (Tomasi et al., 2005). Furthermore, no clear variation between years was detected over this period during our 3-year follow-up (results not shown). Concerning leaf orientation, by contrast, we decided to perform the digitalization only once in spite of evidence for variations throughout the season in other species (Thanisawanyangkura et al., 1997; Takenaka et al., 2001). This should be checked on a finer scale before any generalization, but even if several dates were finally required, inter-annual validity of the distributions can reasonably be expected. Overall, the initial parameterization of a C × T pair remains a demanding task. The time required is estimated at the equivalent of digitizing two to three plants (1½ d). However, this approach opens up new avenues of investigation thanks to the possibility of saving measurements. It can be used to represent the canopy structure at any time during the flowering–harvest period, from measurements (discontinuous) or simulations (continuous, Louarn et al., 2007) of mean shoot characteristics (shoot leaf area, number of leaves, branching pattern).

The generated 3D virtual scenes were assessed at different levels. We first checked the consistency of the values taken by each parameter in the different situations studied. As expected from published results (OIV, 1983), the shoots of ‘Grenache’ were more erect (as shown by their generally higher α_s and lower ϕ_s) than those of ‘Syrah’. Moreover, the distributions of α_s, ϕ_s and θ_s depended on trellising intensity (Winkler et al., 1974), whereas the two parameters defining leaf orientation were affected principally by the openness of the canopy, as suggested by Smart et al. (1982) and Mabrouk et al. (1997a). Thus, the defined simplified set of parameters was clearly able to capture a major part of the variability between C × T pairs.

Quantitative model assessment was initially carried out at canopy level, by comparing the measured ε_i at various positions in actual vineyards with ε_i values calculated from generated virtual scenes (Andrieu et al., 1995). We assessed separately the capacity of the model to reconstruct a given situation (VHI_pf, test of the mean shoot hypothesis and of the spatial leaf area distribution procedure, using measured parameters) and the procedures used to generate new sets of parameters using stochastic methods (VHI_fr). In both rounds of simulation, the simulated ε_i values were highly consistent with the measured values. RMSE values were in the range of measurement error for these variables in the field (Louarn et al., 2005) and the observed variability at each position was correctly simulated. This demonstrates (1) the ability of the model to represent a wide range of situations at the canopy scale as long as the 3D paths of the main axes are accurately described, and (2) the reliability of the multivariate approach used for generating such 3D paths. The results also confirmed that the level of plant-to-plant variability is high in vineyards, even for trellised and summer-pruned training systems (Casteran et al., 1980). This variability potentially has an impact on fruit ripening (Bergqvist et al., 2001; Spayd et al., 2002) and is clearly not taken into account when plots are described on the basis of a very limited number of fully digitized vines (Fig. 9; Mabrouk et al., 1997a,b; Mabrouk and Sinoquet, 1998). Such an approach can lead to significant bias in the estimation of light interception, depending on the extent to which the sampled plants may be considered to be representative. Statistical modelling approaches clearly make a positive contribution in this case, because the inter-plant variability for a given C × T pair may exceed the mean difference between two C × T pairs. Variability must therefore be correctly integrated into the analysis if different situations are to be compared properly.

We then assessed the model at the individual plant scale, comparing radiative balances of fully digitized vines with those computed on their corresponding simulations. The distribution of leaf area into classes of daily cumulative intercepted radiation was correctly predicted in all situations. Thus, despite inaccuracies in predicting the spatial positioning of individual leaves, organ population characteristics, such as the shape of the distribution of light interception at the organ scale, can be inferred from statistical reconstructions and used to compare different C × T pairs. This trait is indeed theoretically linked to the potential exposed leaf area (Carbonneau, 1995), an empirical indicator broadly used in viticulture to predict productivity and harvest quality (Kliewer and Dokoozlian, 2005). However, for particular individual organs, the results suggested that light interception may be slightly underestimated. Consequently, the output of the model may not be suitable for predicting absolute light interception (Sonohat et al., 2006). The reorientation of leaves according to the surrounding light microclimate (Smart et al., 1982; Caldwell, 1987; Niinemets and Kull, 1995; Stenberg et al., 1999; Takenaka et al., 2001) may be involved. The implicit hypothesis of independence between leaf orientation and 3D leaf positioning usually made in reconstruction models is probably not respected, even here where the row canopy has been split into north and south sides to account for preferential leaf azimuth. The resolution of this problem constitutes an inviting track to follow in order to improve the predictions of this kind of model.

CONCLUSIONS

The results of the present study demonstrate the potential use of statistical reconstruction models combining pragmatic simplifications of plant architecture with Monte Carlo samplings to generate geometric 3D mock-ups reliable for a wide range of grapevine cultivars and training systems. We focused particularly on establishing a trade-off between data acquisition for a given situation and the accuracy of representation of the main variables involved in C × T pair differentiation (light interception efficiency, LAD, light microclimate), sometimes at the expense of visual realism and of the potential insight of virtual plants (the absence of a topological relationship between the axillary leaves implies that no insight can be obtained below shoot level). The approach developed here was dedicated to grapevine, but the same free tools (ALEA platform, Pradal et al., 2004) could be used to develop modified, simple-to-use reconstruction procedures for other plant canopies, or even for roots, which are also known to display strong architectural plasticity (Lynch, 1995). For instance, a declination of the present version based on a whole-plant envelope has recently been presented on cotton (Martin et al., 2007).

In grapevine, the estimation of light interception at plot scale was significantly more accurate with statistical reconstruction than with approaches derived from the duplication of a single fully digitized plant. The next step to compare properly the various C × T pairs will be to use the validated 3D reconstruction model to quantify the impact of management practices on LAD, light interception and light microclimate for a relevant number of plants. As the model is embedded in a platform dedicated to the analysis of 3D plant architecture, this last step is facilitated by the compatibility of model outputs with several functional tools (ARCHIMED, Dauzat and Eroy, 1997; RATP, Sinoquet et al., 2001). Finally, in the medium term, it should be possible to couple this model with ecophysiological models of shoot growth and development (Lebon et al., 2006; Louarn et al., 2007), to generate mean shoot characteristics in response to environment. This coupling of different models should transform the current mostly static description of 3D structure into a truly dynamic description.