Water Replacement Hypothesis in Atomic Detail—Factors Determining the Structure of Dehydrated Bilayer Stacks

Abstract

According to the water replacement hypothesis, trehalose stabilizes dry membranes by preventing the decrease of spacing between membrane lipids under dehydration. In this study, we use molecular-dynamics simulations to investigate the influence of trehalose on the area per lipid (APL) and related structural properties of dehydrated bilayers in atomic detail. The starting conformation of a palmitoyloleolylphosphatidylcholine lipid bilayer in excess water was been obtained by self-assembly. A series of molecular-dynamics simulations of palmitoyloleolylphosphatidylcholine with different degrees of dehydration (28.5, 11.7, and 5.4 waters per lipid) and different molar trehalose/lipid ratios (<1:1, 1:1, and >1:1) were carried out in the NPT ensemble. Water removal causes the formation of multilamellar “stacks” through periodic boundary conditions. The headgroups reorient from pointing outward to inward with dehydration. This causes changes in the electrostatic interactions between interfaces, resulting in interface interpenetration. Interpenetration creates self-spacing of the bilayers and prevents gel-phase formation. At lower concentrations, trehalose does not separate the interfaces, and acting together with self-spacing, it causes a considerable increase of APL. APL decreases at higher trehalose concentrations when the layer of sugar physically separates the interfaces. When interfaces are separated, the model confirms the water replacement hypothesis.

Introduction

Life exists in water and depends on water because the hydrophobic effect is a major driving force in the self-assembly of cellular membranes and in protein folding (1). Water removal normally causes irreversible structural changes in biological systems and loss of viability. Desiccation-tolerant or anhydrobiotic organisms can survive severe dehydration to a few percent of water (2). Membranes are considered a primary target of dehydration injury. Disaccharides can prevent fusion and loss of membrane integrity associated with dehydration in natural and model membranes (3–5). The nonreducing disaccharide trehalose is most effective for membrane protection. A number of applications for trehalose have been reported, including dry stabilization of vaccines, liposomes (6,7), and human blood cells (8). The latter has the potential to change blood banking. For all of these applications, we need a better understanding of the mechanisms underlying dry membrane protection by sugars.

Fourier transform infrared spectroscopy and differential scanning calorimetry have shown that disaccharides prevent the increase of the gel-to-liquid phase transition temperatures T_m of dehydrated lipid bilayers (4,5). There are two main hypotheses to explain this. According to the water replacement hypothesis (3,4) disaccharides replace water molecules that interact with polar headgroups of lipids and thus maintain sufficient spacing between lipids to keep the acyl chains in a liquid-crystalline state. An alternative hypothesis suggests that depression of T_m in dry phospholipids by sugars may be due solely to vitrification of sugars (9,10). There are strong arguments in favor of water replacement (11). However, recent publications have shown that sugars are excluded from dry bilayers (12,13), motivating further studies of the ability of sugars to create spacing in dry lipid bilayers.

The spacing between lipids within the bilayer can be quantified by the area per lipid (APL) at the bilayer interface. This structural property relates to the physical state of the hydrocarbon chains (14). The APL is inversely proportional to the mean thickness of the bilayer and decreases with increasing membrane order; therefore, x-ray (14–17) and nuclear magnetic resonance (NMR) (18,19) experiments can be used to determine the APL.

The APL in bilayers of lipids of the phosphatidylcholine (PC) family does not change during lipid dehydration if 12–13 waters per molecule remain, but it decreases with further dehydration (20). Experiments on the effect of trehalose on APL of PC bilayers are sparse. Crowe et al. (21) showed that trehalose causes a concentration-dependent increase of APL in dipalmitoylphosphatidylcholine (DPPC) monolayers. There are no direct experimental data demonstrating that trehalose causes an increase of APL in dry bilayers; however, this has been shown indirectly by decreasing phase transition temperatures (4,5). Disordering of the acyl chains of dry DPPC in the presence of trehalose, as determined by solid-state NMR, also indicates an increase of APL (22,23).

Molecular-dynamics (MD) simulations yield an atomically detailed picture of lipid bilayer structure (24,25). Simulations of dioleoylphosphatidylcholine (DOPC) (26) and dimyristoylphosphatidylcholine (DMPC) bilayers (27) at different levels of hydration have shown decreasing APL with water removal. In one study, the structure of a fully hydrated DPPC bilayer was largely unaffected by trehalose (28). In a recent study of the interactions of trehalose with a lipid bilayer at low water content, the authors focused on the formation of hydrogen bonds between trehalose and bilayers (29).

The purpose of this work was to study in atomic detail the factors that determine the APL of the lipid bilayer at different water and trehalose contents to validate or disprove the water replacement hypothesis. Palmitoyloleolylphosphatidylcholine (POPC), the most abundant lipid in biological membranes, was used. The bilayer was simulated at full hydration (28.5 waters per lipid) and at intermediate (11.7 waters per lipid or 27.8% water content on a dry weight basis) and low (5.4 waters per lipid or 12.8% on a dry weight basis) water contents. At intermediate water content, the headgroups remained hydrated, whereas the interbilayer water layer was removed. At low water content, the headgroups were partially dehydrated.

Materials and Methods

Simulation details

Here we discuss the simulations briefly; details are provided in the Supporting Material. A united atom description for the lipids was used. Parameters for bonded and nonbonded interactions were taken from a study of DPPC bilayers (30), available at http://moose.bio.ucalgary.ca/files/lipid.itp. Partial charges were obtained from Tieleman and Berendsen (31) and can be found at http://moose.bio.ucalgary.ca/files/popc.itp. The SPC water model (32) was used. The starting bilayer configuration was previously created manually (31) by placing lipid molecules on a grid. Simulations were performed using Gromacs 4 (33). The self-assembly of the bilayer from a random mixture of lipid and water molecules is another way to obtain the initial bilayer configuration (34). We applied the self-assembly of POPC to validate the simulation and force-field parameters. We performed the simulations with 256 lipids and a range of water and trehalose concentrations using standard techniques (35,36); the detailed systems and nomenclature are described in Table 1.

Table 1.

Stack model compositions and nomenclature used in this work

Model name	Lipids/box	Water/lipid	Trehalose/box	Trehalose/lipid
h28-00	256	28.5 fully hydrated	0	0
s11-00	256	11.7 intermediate	0	0
s11-a	256	11.7 intermediate	160	<1:1, low
s11-b	256	11.7 intermediate	256	1:1, intermediate
s11-c	256	11.7 intermediate	320	>1:1, high
s5-00	256	5.4 low	0	0
s5-a	256	5.4 low	128	<1:1, low
s5-b	256	5.4 low	256	1:1, intermediate
s5-c	256	5.4 low	320	>1:1, high

Analysis methods

Standard techniques were used as described in the Supporting Material. To calculate the main structural dimensions of the bilayer from the density profiles, we used the following definitions: The position of the interface is defined as the point where the water (solvent) density equals the lipid density (37). Solvent density is the sum of trehalose and water densities. The bilayer thickness (D_B) is the distance between two interface planes within the bilayer. The interbilayer water (solvent) thickness D_W (D_S) is the distance between two interface planes of adjacent bilayers. The peak-to-peak separation (PP) is the distance between two lipid peaks within one bilayer. The peak-to-peak distance PP1 is the distance between two lipid peaks of neighboring interfaces. The width of the interface is the distance along the bilayer normal, where water density decreases from 90% to 10% of maximum.

Results

APL under dehydration

Fig. 1 A shows the evolution of the APL during the simulation of the POPC bilayer at different water contents. Equilibrium was attained after 100 ns, so we average over the last 100 ns. Since the exponentially fitted APLs are close to the averaged APLs (Fig. 1 A and Table 2), we do not discuss them separately. We find an APL in the fully hydrated bilayer (h28-00) of 0.693 ± 0.008 nm² (Table 2). This is 0.03 nm² higher (0.66 nm²) than the literature average for experimental (38–42) and MD (43–47) data. A similar discrepancy was observed in simulations of DMPC (27). It was also reported that the average APL increases with simulation size in an NPT ensemble (48). In our preliminary simulations with 64 lipids per box, we obtained APL = 0.66 nm² over 20 ns. Here (Fig. 1 A), the APL of the 256 lipid system at 20 ns is also close to 0.66 nm², but the bilayer is not equilibrated.

Figure 1.

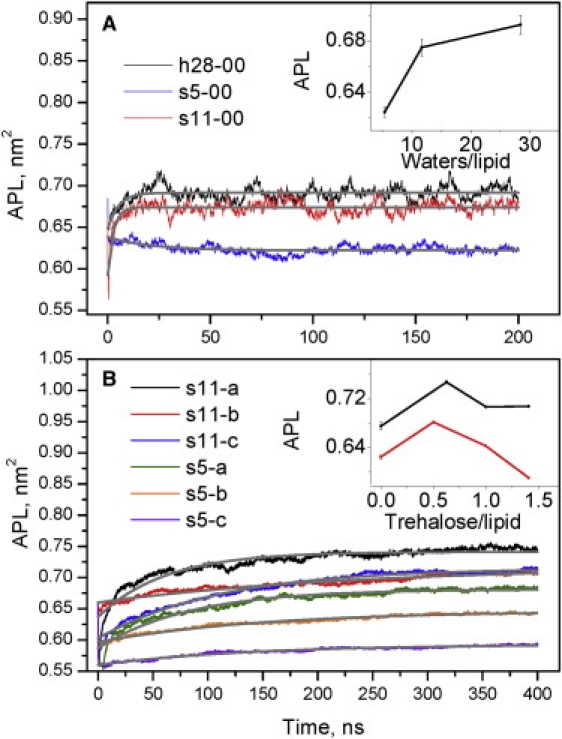
(A) Time evolution of the APL with different water contents; (inset) effect of dehydration. (B) Evolution of the APL with different trehalose contents at low and intermediate levels of dehydration; (inset) effect of trehalose on APLs. Gray thick lines are the fits y = A₁^∗exp(-x/t₁) + y_0. The SD is indicated; when error bars are not visible, they are smaller than the symbols.

Table 2.

APL (nm², averaged and fitted) and structural parameters of bilayers derived from the mass density profiles (see the text for definitions; all distances are in nanometers)

	APL averaged nm2 ± SD∗	APL fitted nm2 ± SE†	DB ± SE‡	P-P ± SE	P-P1 ± SE	DW or DS ± SE	% overlap ± SE§
h28-00	0.693 ± 0.008	0.69153 ± 0.00013	3.96 ± 0.05	2.69 ± 0.05	3.50 ± 0.05	2.24 ± 0.03	0.21 ± 0.10
s11-00	0.675 ± 0.007	0.67403 ± 0.00012	4.11 ± 0.01	3.07 ± 0.13	1.63 ± 0.12	0.58 ± 0.01	27.72 ± 7.08
s5-00	0.624 ± 0.004	0.62236 ± 0.0001	4.54¶ ± 0.01	3.41 ± 0.02	1.15 ± 0.02	n.d.	63.17 ± 2.94
S11-a	0.747 ± 0.003	0.74141 ± 0.00013	3.50 ± 0.01	2.31 ± 0.08	2.62 ± 0.07	1.40 ± 0.02	23.74 ± 0.29
S11-b	0.707 ± 0.002	0.71821 ± 0.00039	3.66 ± 0.01	2.66 ± 0.02	2.91 ± 0.01	1.90 ± 0.01	1.24 ± 0.06
S11-c	0.709 ± 0.003	0.71515 ± 0.0001	3.55 ± 0.04	2.33 ± 0.04	3.70 ± 0.06	2.51 ± 0.02	1.07 ± 0.03
S5-a	0.682 ± 0.002	0.68136 ± 0.00011	3.78 ± 0.01	2.31 ± 0.08	1.92 ± 0.03	0.87 ± 0.01	43.32 ± 0.8
S5-b	0.643 ± 0.001	0.64688 ± 0.0001	3.93 ± 0.01	2.67 ± 0.02	2.31 ± 0.01	1.64 ± 0.01	9.3 ± 0.3
S5-c	0.591 ± 0.001	0.59288 ± 0.00008	4.15 ± 0.01	2.33 ± 0.04	3.62 ± 0.02	2.37 ± 0.01	2.3 ± 0.03

^∗SD was calculated for APL averaged within 320–400 ns.

^†Evolution of APL in time is fitted by the function y = A₁^∗exp(−x/t₁) + y₀; y₀ is presented as the fitted APL ± SE.

^‡Time interval from 370 to 380 ns, for which the density profile is plotted in Fig. 2, is split into 2 × 5 ns intervals, and the structural parameters are calculated for each interval and averaged ±SE.

^§Lipid interface overlap is calculated as the percentage of lipid density in the middle of the interbilayer space from the maximal lipid density.

^¶See text; n.d.—not detectable.

According to the water replacement hypothesis, the spacing between lipids decreases with dehydration. Because the size of the PC hydration shell is ∼12 waters per lipid (20), only water removal below 12 waters per lipid (Hristova point) is expected to cause dehydration and change the bilayer properties. The APL decreases only slightly at 11.7 waters per lipid (0.675 ± 0.007 nm²) in comparison with 28.5 waters per lipid (Table 2). A significant decrease to 0.624 ± 0.004 nm² occurs when the bilayer contains 5.4 waters per lipid. The break at 11.7 waters/lipid (Fig. 1 A, inset) correlates with the estimated size of the hydration shell for PC (20). Thus the dependence of APL on water content shown here agrees well with experiments. However, APL at low water content (0.624 ± 0.004 nm², Table 2) does not appear in the gel state, which would be expected at 5.4 waters per lipid. A similar discrepancy was observed in simulations of DOPC (26) and DMPC (27) in which the APL at low water content (5.4 and 5 waters per lipid, respectively) was higher than in the gel state.

Effect of trehalose on the APL of dehydrated bilayers

Fig. 1 B shows the evolution of APL during the simulation at intermediate (s11) and low (s5) water contents with trehalose. Near-equilibrium conditions were attained after 320 ns, so we average over the last 80 ns. The remaining slight drift is considered in the fitting and does not influence the calculated values. The water replacement hypothesis suggests that trehalose increases the spacing between lipids in the dry bilayer to the values of the hydrated one. At low trehalose content, we observe an increased APL for both s5 and s11 (Fig. 1 B, inset). In the s5-a model, the APL is close to the hydrated bilayer (Table 2). The combination of low water and low trehalose content behaves as expected from the water replacement hypothesis. However, in the model s11-a, the APL is much higher than with the full hydration (Table 2). Here trehalose disturbs the bilayer rather than stabilizing it. A further increase in trehalose concentration causes the APL to decrease (Fig. 1 B, inset). One trehalose or more per lipid at intermediate water content (s11) keeps the APL close to a fully hydrated bilayer. At low water content (s5), the APL gradually decreases with increasing trehalose (Fig. 2 B, inset). The values are below the fully hydrated bilayer, and for s5-c even below the dry bilayer without trehalose (s5-00). This effect of trehalose concentration on the APL in dry bilayers disagrees with the water replacement hypothesis.

Figure 2.

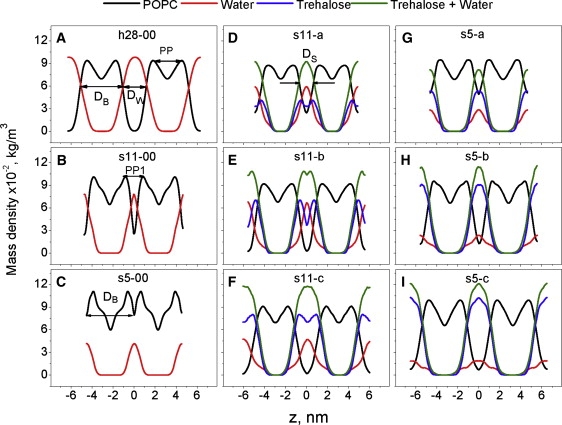
Mass density profiles of POPC, water, trehalose, and trehalose+water for different systems as designated in Table 1. Leaflets of adjacent bilayers through periodic boundary conditions from both sides are shown for clarity. All profiles are centered in the interbilayer space.

Mass density profiles

Mass density profiles and structural dimensions are presented in Fig. 2 and Table 2. In the fully hydrated model h28-00, the bilayer thickness D_B is 3.96 ± 0.05 nm, whereas the PP is 2.69 ± 0.05 nm (Fig. 2 A, Table 2). The thickness of the headgroup outward from the density peak is thus 0.64 nm. The interbilayer water thickness is 2.24 ± 0.03 nm, with a small part of the constant water density (Fig. 2 A) being bulk water. The remaining interbilayer water is within the interface with protruding lipids. The width of the interface is ∼1.2 nm, in accordance with the literature (49).

At intermediate water content (s11-00), the interbilayer water thickness is reduced to 0.58 ± 0.01 nm, with no bulk water (Fig. 2 B, Table 2). The interfacial regions of neighboring bilayers merge. The lipid density in the middle of the interbilayer space increases to 27.72% ± 7.08% of the maximum. At low water content (s5-00), we cannot define an interface plane, because at no point does the water density rise above the lipid density (Fig. 2 C). In this case we calculated D_B (Table 2) as the distance between two minima of lipid density at the interfaces of the two leaflets (Fig. 2 C). There is only interfacial water. The lipid density in the center of the interbilayer space is 63.17% ± 2.94% of maximum. It can be interpreted as the interpenetration of two neighboring membranes via periodic boundary conditions. The overlap of the headgroups at low water content (5.4 waters/lipid) was observed by Mashl et al. (26) in DOPC and by Essman et al. (50) in DPPC at 11 waters per lipid. This overlap may explain the higher-than-expected APL for the dehydrated bilayer.

The decrease of APL under dehydration is accompanied by the increase of PP and D_B (Table 2; see Fig. S2 in the Supporting Material). The degree of interpenetration decreases with trehalose, but remains higher for s5 than for s11 (Table 2, Fig. S3). Apparently, the deeper the interpenetration, the more trehalose is needed to separate the bilayers. When there is not enough trehalose to separate the two bilayers (<1:1), PP is the lowest and APL the highest in both the s5 and s11 models. When the two interfaces are separated, PP increases and APL decreases (Table 2).

Radial distribution functions between N and P of neighboring interfaces

The interpenetration of headgroups of adjacent bilayers can be resolved by radial distribution functions (RDFs) and 2D RDF maps between nitrogens (N) from one interface and phosphorus or nitrogens from the neighboring layer (p and n) plotted with respect to N-p and N-n atomic distances (Fig. 3). In the fully hydrated case (h28-00, Fig. 3 A), the RDFs between N-n and N-p gradually increase at distances of ≥2 nm, in agreement with the PP1 distance of 3.50 ± 0.05 nm (Table 2). The blue area in the 2D map visualizes the separation.

Figure 3.

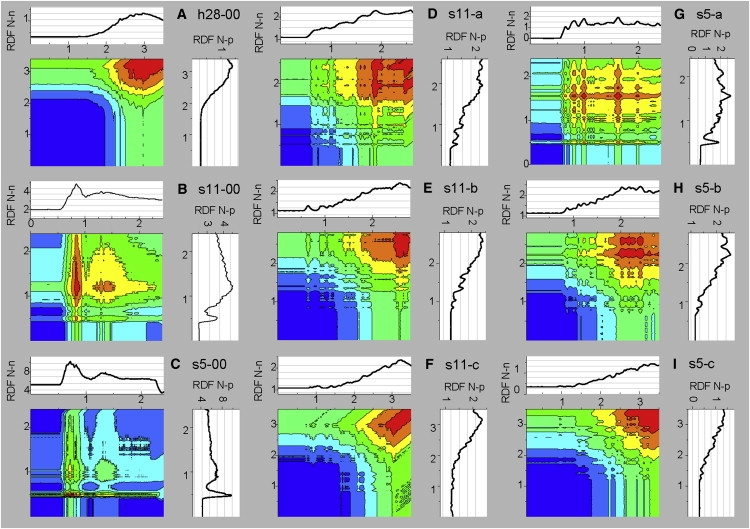
RDFs between N-n (top) and N-p atoms (right) from headgroups of adjacent bilayers, and 2D maps correlating RDF (N-n) and RDF (N-p) for models with different water and trehalose contents. All distances are in nanometers. Blue indicates the minimal level (close to zero) and red indicates the maximal level of RDFs.

At intermediate water content (s11-00, Fig. 3 B), the position of the first RDF peak is ∼0.5 nm for N-p and 0.84 for N-n. At low water content (s5-00), this decreases to 0.48 nm and 0.74 nm, respectively (Fig. 3 C). The N-p distances are shorter than the N-n distances due to the methyl groups around the nitrogens. These distances are less than half of the PP1 distances of 1.63 ± 0.12 nm (s11-00) and 1.15 ± 0.02 nm (s5-00, Table 2) showing that P and N atoms cross from one interface into the other. The probability of close N-p contacts increases with decreasing water content (Fig. 3, A–C).

In s11-a we see only a few close (r < 1 nm) N-p and N-n contacts (Fig. 3 D). The solvent thickness D_s is 1.40 ± 0.02 nm and the lipid density in the interbilayer space is 23.74% ± 0.29% (Table 2). The RDF peaks at intermediate trehalose content (s11-b, Fig. 3 E) become negligible and disappear at higher trehalose content (Fig. 3 F; see also Fig. S3). The neighboring interfaces are separated without close contacts between atoms of two adjacent monolayers. The solvent layers have the same thickness as in the hydrated model, and no lipids are in the interbilayer space. At low water content (s5) the population of close N-p and N-n pairs decreases, but is still substantial at low trehalose content (s5-a, Fig. 3 G). This correlates with the thin solvent layer of D_s = 0.87 ± 0.01 nm and high lipid density in the interbilayer space (43.32% ± 0.8%, Table 2). We find a much stronger interpenetration of interfaces in s5-a than in s11-a, in agreement with the data in Table 2 and Fig. S3. The close contacts across water become negligible at intermediate trehalose (s5-b, Fig. 3 H) and disappear at high trehalose content (s5-c, Fig. 3 I). The shapes of the 2D maps are almost identical as long as the interfaces are separated by ≥2 nm (Fig. 3, A, E, F, and I). The map for s5-00 (Fig. 3 C) is different, showing that practically all P and N are in close contact with the next layer. In s11-00 (Fig. 3 B), only some atoms are in close contact, correlating with the lipid density in the interbilayer space.

Influence of dehydration and trehalose on PN vector orientation

The APL is very sensitive to the detailed interplay between perpendicular and in-plane components of headgroup dipoles (51), which depend on the PN vector orientation. There is a wide symmetric distribution of PN vector orientations in h28-00, with a maximum (average orientation) corresponding to ∼75° (Fig. 4 A). This agrees with previous simulations (50,52,53) and experiments (54). With dehydration the orientation distribution becomes asymmetric, with a maximum at larger angles (Fig. 4, B and C). For both hydrated and dehydrated bilayers, the distribution can be fitted by two Gaussians for two distinct conformations of headgroups in hydrated DPPC bilayers (53,55). In the hydrated bilayer, the smaller population is ∼50° and the larger one is ∼80° (Fig. 4 A). With dehydration the average position of the smaller population stays around 50–55°. The position of the larger one shifts to higher angles. The average is 87° (Fig. 4 B) at intermediate water content and 91° at low water content (Fig. 4 C). This means that in the dehydrated bilayer, a considerable number of choline groups point inward. Similar behavior was found in previous simulations of DOPC (26) and studies that used NMR for DOPC (56) and POPC (57). Since the PN vector has a large dipole moment, the tendency to orient its dipoles parallel to the surface is favorable in terms of electrostatic interactions. This explains the orientation of the PN vector in dehydrated bilayers. In fully hydrated bilayers, the dipole interactions are weak due to shielding by water, and the parallel orientation is not favored as much. Smondyrev and Berkowitz (58) showed that the PN vector has a higher probability of orienting parallel to the surface and even to point inside for DPPC in DMSO. Additionally, larger motional freedom in the water phase and steric requirements opposing parallel orientation result in a preferential outward orientation of PN vectors in full hydration.

Figure 4.

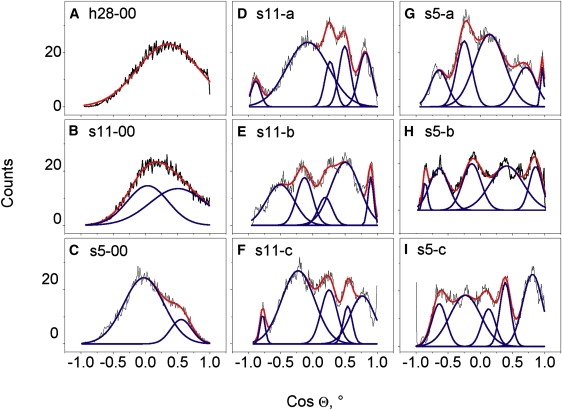
Orientation of PN vectors in the bilayers (cosine of the angle of the headgroup with the bilayer normal) with different water contents (A–C), at intermediate water content and different amounts of trehalose (D–F), and at low water content and different amounts of trehalose (G and H). Designation of the models is described in Table 1.

In dehydrated bilayers with trehalose, there are no strongly preferred orientations (Fig. 4, D–I). We approximate the distribution with five Gaussians. A large fraction points inward at any trehalose concentration. NMR experiments have revealed parallel orientations for hydrated POPC bilayers with trehalose (59). The effect of trehalose on PN orientation is concentration-dependent (59) and has been attributed to dehydration of the membrane surface (57). Parallel orientations in the presence of aqueous and hydrophobic anions and negatively charged amphiphiles have also been shown by NMR (60,61) and MD (53). The broad distribution of PN vectors without preferential orientation in dehydrated bilayers with trehalose probably results from both electrostatic and dynamic effects. Since trehalose immobilizes headgroups, the orientations are not averaged completely within the simulation time. The dipole moment of PN can be partly compensated for by trehalose, and the parallel orientation to the bilayer surface is less favored.

Lipid potential

The lipid potential is determined mainly by distributions of negative P and positive N atoms, and the orientation of the PN vectors with the bilayer. The overlap of interfaces upon dehydration changes the RDFs between P and N atoms of neighboring interfaces and the distribution of PN vectors. Separation of dry bilayers by trehalose restores the RDFs, but not the distribution of PN vectors. We show the lipid potential and atom distributions along the bilayer normal to demonstrate how dehydration and trehalose change the lipid potential. In h28-00 (Fig. 5 A) the lipid potential builds up across the interface where the P and N atoms are located, and levels off to bulk water (Fig. 2). The lipid potential is positive inside the membrane due to NP vectors pointing toward the water (Fig. 4). The potential under full hydration is 6.04 V, in agreement with literature values (26,62).

Figure 5.

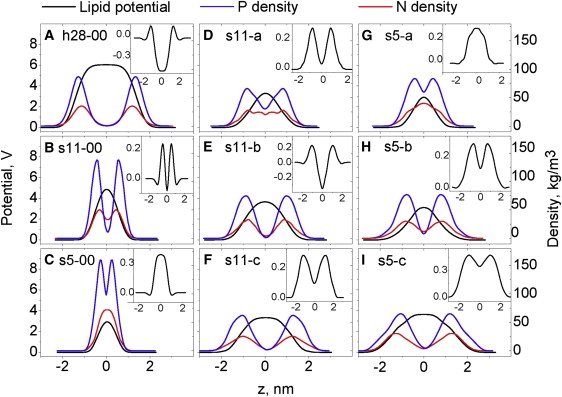
Lipid potentials and mass density profiles of N and P atoms in the bilayers with different water contents (A–C), at intermediate water content and different amounts of trehalose (D–F), and at low water content and different amounts of trehalose (G and H). Designation of the models is described in Table 1. (Insets) Total potential profiles.

When bulk water is removed and the interfaces merge (s11-00, Fig. 2), the N density profiles from neighboring interfaces overlap ∼66%, whereas the P density profiles overlap ∼8% (Fig. 5 B). We calculate the overlap as the P or N atom density at z = 0 as a percentage of their peak values. Obviously, the population of P atoms, which are in the plane at z = 0, have a zero potential with N atoms in the same plane (PN oriented parallel to the interface plane) and a negative potential with N atoms inside the interface (inward PN orientation). In both cases this decreases the lipid potential. For the model s11-00, the lipid potential is ∼4.9 V (Fig. 5 B). In s5-00, the overlap is 100% and ∼62% for N and P distributions, respectively (Fig. 5 C), resulting in a lipid potential of ∼2.6 V. Trehalose in the s11-a model does not separate, but increases the overlap of P and N distributions to ∼74% and ∼45%, respectively (s11-a, Fig. 5 D). This correlates with the increase of APL above full hydration values (Fig. 1 B). The increasing population of P atoms in the interbilayer space decreases the lipid potential to ∼2.4 V. The P and N atoms from neighboring interfaces are separated at higher trehalose contents (Fig. 5, E and F). The shape of the lipid potential profiles becomes similar to the hydrated bilayer (Fig. 5 A) without reaching the same value.

In s5-a, trehalose does not separate the bilayer and N distributions have 100% overlap (Fig. 5 G), resulting in one peak as in s5-00 (Fig. 5 C). P distributions have separated peaks with ∼72% overlap and a lipid potential of ∼1.8 V (Fig. 5 G). Higher trehalose concentrations cause the interfaces to separate, but the lipid potentials remain ∼1.7–1.8 V (Fig. 5, H and I). Thus, the interface interpenetration causes the overlap and decrease of the lipid potential. Trehalose at medium and high concentrations separates the interfaces but does not restore the lipid potential. This is probably due to parallel and inward-oriented PN vectors in dry bilayers with trehalose (Fig. 4, D–I).

Water and sugar potentials

Because water orients in the headgroup area to compensate for the lipid potential (63), the water potential is negative and almost mirrors the lipid potential (Figs. 5, A–C, and 6 A). The plateau in the water potential in h28-00 corresponds to bulk water, where the molecules are randomly oriented and do not see the lipids (Fig. 2 A).

Figure 6.

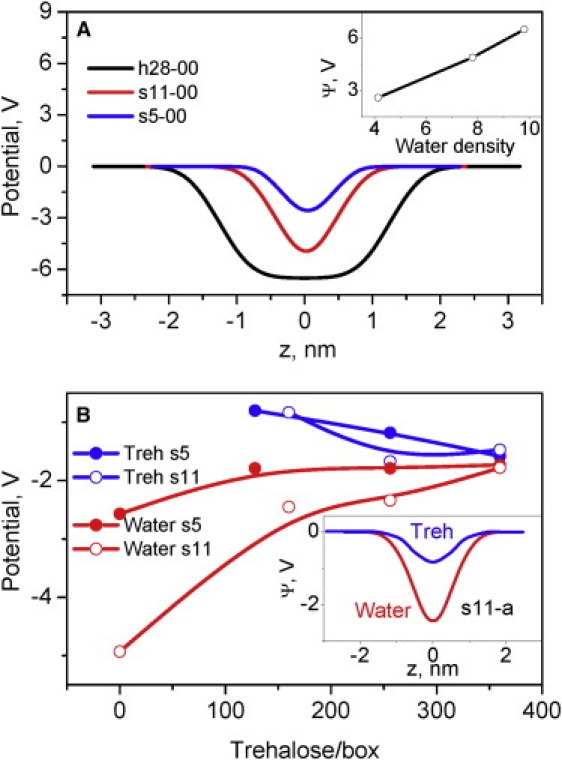
(A) Water potential profiles in the bilayers with different water contents; (inset) correlation between water potential and density at z = 0. (B) Changes in water and trehalose potentials in models with different water and trehalose contents; (inset) potential profiles.

The value of the water potential decreases with water removal from 6.5 V for the fully hydrated bilayer to 5.0 and 2.6 V for intermediate and low water contents, respectively. In contrast to the lipid potential, the water potential is proportional to water density (Fig. 6 A, inset). When trehalose is added, the sugar produces a negative potential, partly compensating for the lipids (for example, see model s11-a in Fig. 6 B, inset). In both the s5 and s11 models, the trehalose potential becomes more negative with increased trehalose (Fig. 6 B). In contrast, the water potential becomes less negative with trehalose (Fig. 6 B), possibly due to water redistribution from lipids to trehalose.

Total potential

The shape of the total potential profile reflects the interface position. In h28-00 it contains two separated positive peaks with a negative plateau of −0.46 V in the interbilayer space (Fig. 5 A, inset) due to overcompensation for the lipid potential (+6.04 V) by water (−6.5 V). In s11-00 two interfaces just merge, and the shape of the total potential has two close peaks with slightly negative minima in the middle of the interbilayer space of −0.08 V (Fig. 5 B, inset), indicating that the water compensates for the lipid potentials. The overcompensation in h28-00 may come from interbilayer free water, which is absent in the s11-00 model (Fig. 2 B). In the dehydrated bilayer s5-00, there is only one positive peak of +0.4 V (Fig. 5 C), indicating that the water does not compensate for the lipid potential. A similar sign reversal of the total potential was previously observed for DOPC at the same water contents of 11.4 and 5.4 waters per lipid (26). This may be partly due to insufficient water around the charges. Interpenetration of interfaces also can decrease the water potential due to the high charge density and disturbance of water orientation around the charges, leading to insufficient compensation for the lipid potential and a reversed sign of the total potential.

A low concentration (s11a) of trehalose does not separate the interfaces. The total potential (Fig. 5 D) has two peaks with minima of +0.04V at z = 0. Higher trehalose concentrations separate the interfaces, and the two peaks of the total potential move away from each other in proportion to trehalose. The total potential profile in s11-b (Fig. 5 E, inset) is similar to h28-00 (Fig. 5 A, inset) with a minimum of −0.35 V. In s11-c (Fig. 6 F, inset) we find two well-separated peaks with minima of +0.09 V.

The bell shape of the total potential in s5-a (Fig. 5 G) is similar to that of s5-00 (Fig. 5 C) and correlates with deep interpenetration of the interfaces (Fig. S3). The total potential remains strongly positive (+0.3 V). At higher trehalose concentrations the total potential exhibits two peaks with the maxima at the interfaces and the minima in the center of the interbilayer space. The total potential in the minima remains positive at all trehalose concentrations.

Discussion

The purpose of this work was to analyze at atomic levels whether trehalose can prevent the decrease of APL caused by dehydration, as predicted by the water replacement hypothesis. Indeed, dehydration caused a decrease of the APL as predicted. However, we did not obtain the gel state at low water content (s5-00). The analyses of the density profiles and the RDFs between N and P atoms from neighboring interfaces show that in the stack model, headgroups of neighboring interfaces interpenetrate and prevent the gel state. The interpenetration causes self-spacing within monolayers.

Why does interpenetration become possible when two interfaces approach each other? Probably the PN vector orientation is crucial. It influences the perpendicular component of the lipid dipole more dramatically than the in-plane component. The perpendicular component dominates despite its much smaller magnitude (51). In full hydration the PN vector is oriented outward and the normal component of the dipole causes repulsion perpendicular to the plane. At intermediate water content, the PN vector is parallel to the membrane (s11-00, Fig. 4). The perpendicular dipole vanishes and bilayers do not repel but can merge. The protrusions make slight interpenetration possible. At low water content the PN vector is oriented inward (s5-00, Fig. 4) and the perpendicular dipoles are oppositely oriented, resulting in attraction at overlap range and deep interpenetration of two interfaces (see Fig. S4). The in-plane dipole leads to attraction between lipids (51), which increases when the vector is parallel to the membrane (s11-00, Fig. 4). This may decrease the APL even though the headgroups remain hydrated (Fig. 1 A, inset). When the PN vector is oriented inward, the in-plane component of the lipid dipole decreases and the attraction between lipids within the monolayer decreases. This may be another factor, together with self-spacing, that prevents the APL from decreasing to the gel state.

When a low concentration of trehalose is added, the APL increases (Fig. 1 B, inset). In s11-a, trehalose causes a considerable disturbance to the bilayer, with the APL being larger than in full hydration. The APL in s5-a is close to that of the fully hydrated bilayer. In both the s5 and s11 models, the increase of APL is the result of two effects: spacing due to overlap of the interfaces with the inward orientation of the PN vector, and accommodation of trehalose in the headgroup area. In s11-a and s5-a, trehalose does not separate the interfaces (Table 2 and Fig. S3), and spacing caused by trehalose accommodation increases the effect of the headgroup overlapping. The separation of interfaces by trehalose (Table 2, Fig. S3) explains the decrease of APL at higher trehalose contents in s5 and s11 (Fig. 1 B, inset). Here the spacing between lipids is caused only by water and trehalose. The effect of interpenetrating bilayers is not considered in the water replacement hypothesis. Therefore, we cannot compare the effect of trehalose with the water replacement hypothesis when two interfaces overlap. When two interfaces are separated by trehalose, the model corresponds to the conditions of the water replacement hypothesis. At intermediate water content, APL decreases close to the value of the fully hydrated bilayer. This shows that if the headgroups are not dehydrated, trehalose does not influence the spacing between lipids. Obviously, at intermediate water content the spacing between lipids is enough to accommodate trehalose molecules without any changes. In fact, this is the same situation as in the fully hydrated bilayer, where the interactions with trehalose do not change the APL (28).

In s5-b, the decreasing overlap (Table 2, Fig. S3) causes the APL to decrease to the level of s5-00. The full separation of the interfaces by the sugar layer (s5-c) induces a further unexpected decrease of APL below s5-00. This does not contradict the water replacement hypothesis. The value of APL in the model s5-00 was higher than it should be due to dehydration. This is due to self-spacing by interface interpenetration and PN vectors pointing inward. If we could manage to separate two bilayers at low water content by an inert material, the APL would probably be lower than 0.5 nm² because experimentally we would be in the gel state at this water content. In this case, the fact that the APL in s5-c (0.59 nm²) is higher than that in the gel state (<0.5 nm²) is in accordance with water replacement. However, the APL in s5-c is not as high as that in the fully hydrated bilayer. This can be explained by the inevitable additional dehydration of lipids that occurs in our model when anhydrous trehalose is introduced into the system. This is in contrast to the experimental model, in which both lipids and trehalose are hydrated to equal matrix potentials by exposure to a certain relative humidity.

The cell membrane consists of various lipids. We selected POPC because phospholipids are most abundant in membranes. Different interactions between trehalose and membrane lipids with other headgroups may occur. In addition, plasma membranes contain carbohydrates as a part of their glycoproteins and glycolipids, and these carbohydrates may participate in desiccation-tolerant mechanisms. However, that is beyond the scope of this study, the purpose of which was to analyze at the atomic level the validity of the water replacement hypothesis as it has been formulated.

How real is the stack model described in this study? In x-ray experiments, stack models at low water contents are used to determine the physical parameters of bilayers. In this respect, our model fits the conditions for x-ray scattering experiments. If the data on the Bragg spacing of the DOPC bilayer at 5.4 waters/lipid (12) transfer to APL values, the APL will be much higher than expected for the gel phase (0.596 nm² (26)). However, such a system can hardly be found in vivo, where membranes are always separated and embedded into the dry cytoplasmic matrix. We therefore developed an additional model in which bilayers in dehydrated systems are physically separated and avoid contact. Our model is different from the one recently demonstrated by Leekumjorn and Sum (29) in that we effectively use a vacuum layer to separate the membranes. The results will be described in a forthcoming work.

Supporting Material

Further details, descriptions, four figures, and references are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00957-6.