Figure 6.

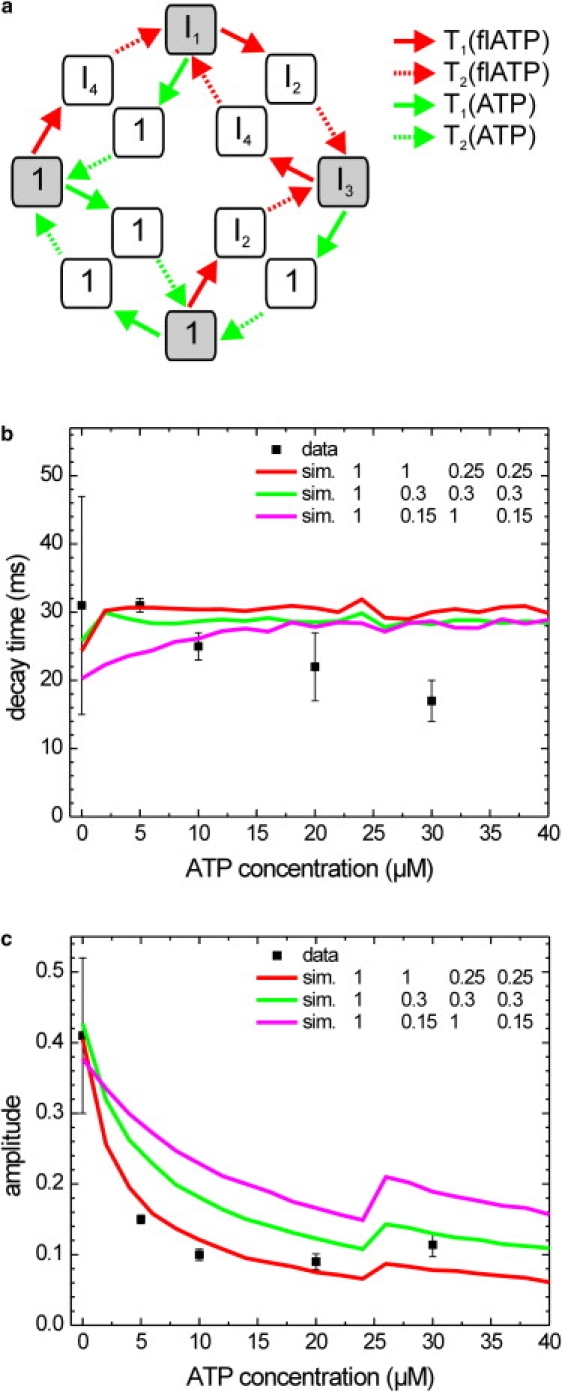
Experimental and simulated decay times and amplitudes of the autocorrelations of donor intensity time traces obtained with mixtures of fluorescent and normal ATP. (a) Schematic representation of the 12-state model used for the simulations. The model is an extension of the one presented in Fig. 5 and it incorporates all the possible conformations and transitions of a single-labeled construct with two types of substrate. The intensities of the states corresponding to those in the four-state model are indicated; the additional states have normal nucleotide bound and consequently intensity 1. Four transition rates are considered, as indicated. T₁ for fluorescent ATP depends on the fluorescent ATP concentration, T₁ for ATP depends on the ATP concentration, and both are calculated using the respective Michaelis-Menten parameters. Both T₂ values are independent of the nucleotide concentrations and are obtained from v_max of the respective nucleotide. The four states on the corners (shaded gray) represent ATP waiting states and act as branching points where a fluorescent or normal ATP can bind. (b) Average (mean ± SE) decay times obtained from exponential fits to the experimental (solid squares with error bars) and simulated autocorrelations of the donor fluorescence intensity (colored lines). For the simulations, a 12-state model was used, corresponding to the model used in Fig. 5a, with additional branching to states with normal nucleotide bound. The three simulations shown correspond to those with the same labeling and color in Fig. 5 (the intensities of other states, with ATP bound, were set to one). (c) Average (mean ± SE) amplitudes obtained from exponential fits to the experimental (solid squares with error bars) and simulated (colored lines) autocorrelations of the donor fluorescence intensity. The discontinuity at 25 μM ATP is caused by the abrupt increase of the fluorescent ATP concentration from 20 to 30 μM, for better comparison with the data.