Characterization of Antibiotic Peptide Pores Using Cryo-EM and Comparison to Neutron Scattering

Abstract

Magainin, a 23-residue antibiotic peptide, interacts directly with the lipid bilayer leading to cell lysis in a strongly concentration-dependent fashion. Utilizing cryo-electron microscopy, we have directly observed magainin interacting with synthetic DMPC/DMPG membranes. Visual examination shows that visibly unperturbed vesicles are often found adjacent to vesicles that are lysed or porous, demonstrating that magainin disruption is a highly stochastic process. Quantitatively, power spectra of large numbers of porous vesicles can be averaged together to produce the equivalent of an electron scattering curve, which can be related to theory, simulation, and published neutron scattering experiments. We demonstrate that magainin-induced pores in lipid vesicles have a mean diameter of ∼80 Å, compatible with earlier reported results in multilayer stacks. In addition to establishing a connection between experiments in multilayer stacks and vesicles, this also demonstrates that computed power spectra from windowed-out regions of cryo-EM images can be compared to neutron scattering data in a meaningful way, even though the pores of interest cannot yet be individually identified in images. Cryo-EM offers direct imaging of systems in configurations closely related to in vivo conditions, whereas neutron scattering has a greater variety of mechanisms for specific contrast variation via D₂O and deuterated lipids. Combined, the two mechanisms support each other, and provide a clearer picture of such ‘soft’ systems than either could provide alone.

Introduction

Magainin 2 is a 23-residue antibiotic peptide isolated from the skin of Xenopus laevis (1). Unlike most commercial antibiotics, which interact with specific protein targets, magainin 2 and other peptides in this class have been shown to interact directly with the lipid bilayer (2,3). Peptides in this class are ubiquitous, with hundreds of identified members (4) over a wide range of species, and they play a critical role in the early stages of host defense (5). Magainin 2 lyses a wide range of both Gram-negative and gram-positive bacteria at concentrations two-orders-of-magnitude lower than those required to lyse red blood cells (6,7). Magainin has also been demonstrated to lyse a range of cancer cells (8,9) at concentrations at which normal tissue is unaffected. For these reasons, peptides in this class are under active development by the pharmaceutical industry. Because they interact directly with the lipid bilayer, it is believed that bacteria will be largely unable to develop resistance to this class of antibiotics.

A wide range of techniques have been used to elucidate magainin's interaction with the lipid bilayer, including fluorescence leakage experiments (10), oriented circular dichroism (11), in-plane neutron and x-ray scattering and lamellar x-ray diffraction (12,13), solid-state nuclear magnetic resonance (14,15), Raman spectroscopy (16), and simulation (17), just to name a few. Several reviews are available with a more complete history of this active field (18–21). Magainin exists as a disordered chain in aqueous solution, and is believed to initially interact specifically with acidic lipids in the bacterial membrane through electrostatic interactions (22). Association with the lipid-water interface induces folding into a single-domain, amphipathic α-helix oriented parallel to the surface of the bilayer. This surface adsorption causes local thinning of the bilayer (13,23). Once a critical concentration of surface-adsorbed peptides is achieved, the peptides spontaneously rotate 90°, forming the boundary of an aqueous pore (Fig. 1) (18,24). It was previously shown by neutron scattering (12) that the pores formed by magainin were larger than anticipated (∼71 Å diameter), and hypothesized that the lipid bilayer itself was also involved in channel formation, with magainin acting as basically a stabilizing agent for a natural transient membrane defect. However, much of the work leading to these previous conclusions was performed using multilayer stacks of lipid bilayers rather than lipid vesicles. That is, many bilayers are forced into close contact in these experiments, and it was unknown what implications this might have, since, in vivo, the peptides would be interacting with isolated vesiclelike membranes. However, the fact that in some cases interactions between neighboring layers or pore-pore correlation were observed in the multilayer stack experiments (25) implied that there may be some differences between the two systems.

Figure 1.

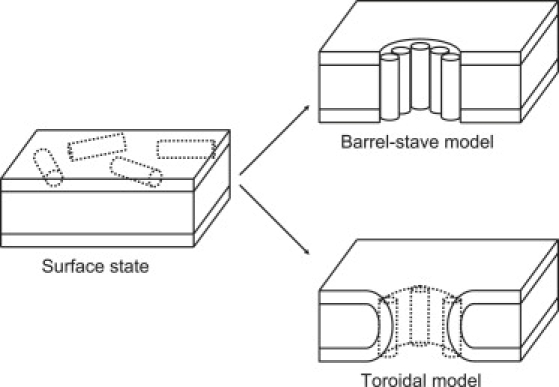
Schematic of possible modes of interaction between amphipathic peptides and lipid bilayers. At low concentration, peptides adsorb to the surface of the lipid bilayer. At higher concentrations, a fraction of peptide molecules rotate to form pores. If the peptide is oriented perpendicular to the membrane, two models must be considered: the barrel-stave channels or the toroidal channels. Previous neutron scattering evidence led to the hypothesis of the toroidal form for magainin channels based on arguments about the amount of peptide available for pore formation.

Cryo-EM and neutron/x-ray scattering have been used together in a cooperative approach in several cases (26–28), and in fact, x-ray solution scattering curves are a highly accurate method for CTF amplitude correction in cryo-EM single particle reconstructions (29,30).

Materials and Methods

Data conventions

Throughout this article, we make use of momentum transfer, q, as traditionally used in the scattering and physics communities in preference to the spatial frequency, s, traditionally used in cryo-EM. The relationship is simply s = q/2π. Spatial frequency is simply the reciprocal of the real-space periodicity of the oscillation. That is, a sinusoidal oscillation with a real-space wavelength of 10 nm would have a spatial frequency of s = 0.1 nm⁻¹.

Materials

1,2-Dimyristoyl-sn-glycero-3-phosphocholine (DMPC) and 1,2-dimyristoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (DMPG) were purchased from Avanti Polar Lipids (Alabaster, AL). Magainin 2 was purchased from Sigma-Aldrich Chemical (St. Louis, MO).

Sample preparation

Liposomes were prepared by mixing a 1:1 ratio of DMPC/DMPG in chloroform/methanol (1:1) and allowing the solvent to evaporate under a dry argon gas flow. The films were kept under light vacuum overnight to remove remaining traces of organic solvent. The resulting dried lipid films were hydrated with distilled water, and the suspension was then extruded using a mini-extruder with a 0.05-μm pore polycarbonate filter (Avanti Polar Lipids) (10). It has been shown by leakage experiments (31–33) that immediately after mixing magainin with vesicles, there is an initial period of high pore density, but that after equilibrium is reached (typically in under 10 min), the open pore fraction has fallen to ∼10% of the peak value. To achieve high pore density, the vesicles were vitrified as quickly as possible after addition of magainin (under 30 s). This is a fundamental difference from neutron scattering experiments in multilayer stacks, which were performed in equilibrium, and thus leaflets could not be defined as inner or outer. Experiments were conducted at various concentrations; the results presented here utilized 400 μM magainin to produce a high surface density. Although lower concentrations (tested down to 40 μM) also produce an effect, the lower pore density produces a much weaker scattering signal. For comparison with previous neutron scattering experiments, we desired a high surface density of pores. The 400-μM concentration used here would correspond to a lipid/peptide molar ratio of ∼25:1 if all magainin were associated with the lipid vesicles. Lipid concentration was determined by phosphorus analysis after extrusion (34).

Vitrification

Before vitrification, all specimen preparation was carried out at 33°C, well above the 24°C phase transition of the DMPC/DMPG mixture (35). It has been previously demonstrated that the vitrification process of the thin films on a TEM grid is so rapid (∼10,000°C s⁻¹), that the system effectively remains in a snapshot of its solution conformation (36,37). Previous experiments with lipid-dense systems have demonstrated that lipid preparations vitrified from higher than the phase-transition temperature will not change state upon vitrification (38). Vitrification was performed in LN₂ cooled liquid ethane using standard procedures on a Vitrobot (FEI, Hillsboro, OR).

Electron cryo-microscopy

All specimens were imaged on a JEM2010F electron microscope (JEOL, Peabody, MA) equipped with a field emission gun operated at 200 keV. Images were collected at 50 K magnification, and defocus ranged from 1.2 to 3.4 μm, putting the first zero crossing of the CTF at q = 0.2–0.4 Å⁻¹, respectively. Images were collected on a 4 K × 4 K charge-coupled device (CCD) camera (model No. US4000, Gatan, Pleasanton, CA) giving images at 2.2 Å/pixel.

Image analysis

Images of vesicles were manually selected (Fig. 2); in the presence of magainin, 69 CCD frames produced 304 magainin-perturbed vesicle images; for the control experiment with no magainin, 64 CCD frames yielded 537 vesicle images. Power spectra were determined by computing the two-dimensional fast Fourier transform (FFT) of each masked image, rotationally averaging the results, then averaging the one-dimensional power spectra from the set of images. The image analysis was performed using the EMAN software package (39). Vesicles from CCD frames were selected using the EMAN command “boxer” with a 320 × 320 box size. Each image was normalized such that the mean density around the edge was zero, then padded with zeroes to 640 × 640 pixels using the EMAN command “proc2d”. The central region of each vesicle was masked using a circular mask (radius = 150 pixels). Next, the squared modulus of the FFT was computed for each image to produce an estimated power spectrum. The masking process eliminates the strong signal produced by the bilayer edge of each vesicle, and limits the curvature of the vesicle surface area under consideration. To reduce noise levels, many such power spectra are then averaged together from many images. The final two-dimensional spectrum is then rotationally averaged to produce a one-dimensional power spectrum. This aggregate process is completed using the “fftavg” program in EMAN (39). The error bars are simply the standard deviation of the mean value at each spatial frequency.

Figure 2.

Typical cryo-EM images of (A) DMPC/PG without magainin (control experiment). (B and C) DMPC/PG with magainin. The bottom three vesicles in panel B have arrows showing strongly perturbed vesicles, and the top three are substantially less disturbed. In panel C, both lysed vesicles and minimally perturbed vesicles are observed. Circles inside vesicles indicate the region extracted for computation of power spectra. Scale bar represents 100 nm.

Background subtraction

As with any scattering experiment, it is necessary to perform background subtraction before modeling of the power spectra. Unlike solution scattering experiments, where a separate scattering experiment is performed for purposes of background subtraction, in cryo-EM this can theoretically be performed using data contained within individual images. Regions in each image where vesicles are not present can be treated as background. These regions are simply ice, with residual solution magainin, and power spectra from these regions can provide background curves for those computed from the center of each vesicle. Unfortunately, although this does a good job of background subtraction (Fig. 3 A), it appears not to account for the entire background at low spatial frequencies in the presence of magainin(q ∼ 0.02–0.05 Å⁻¹), which causes difficulties in modeling, particularly in the high-concentration magainin case.

Figure 3.

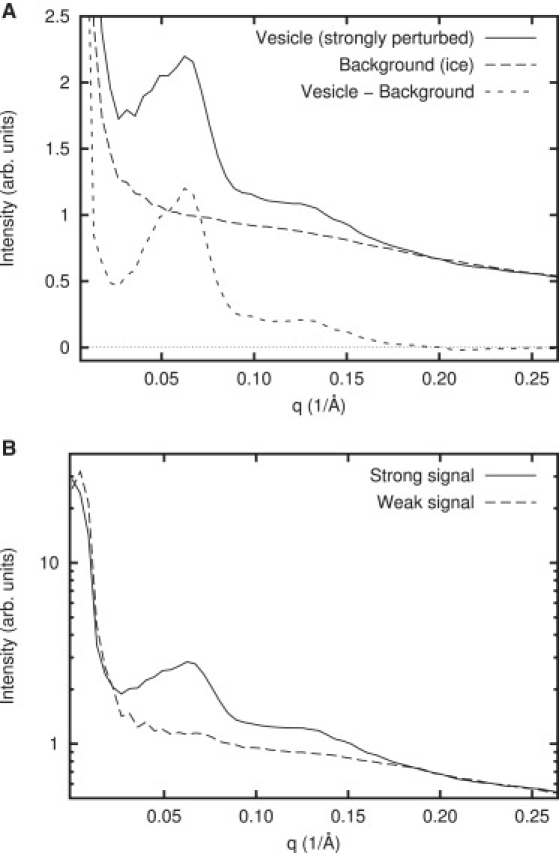
Background subtraction. (A) Example of a raw power spectrum and the background (ice only) subtraction process. The outer region of each vesicle was masked out using a circular mask with a diameter of 66 nm to eliminate the strong signal due to the bilayer edge of each vesicle and to limit the curvature of the vesicle surface. (B) Three-hundred-and-four power spectra from magainin perturbed vesicles including both rough and smooth appearing vesicles were separated into two groups based on peak intensity. The average of 116 strongly peaked power spectra was used as signal, and the average of 188 weakly peaked ones was used as background. The subtraction of the two is the final experimental curve and is used for fitting throughout the data analysis.

In addition, at q < 0.025 Å⁻¹, a sharp peak appears in the power spectrum. This peak is always observed in cryo-EM data, even in images of the background buffer alone. It is believed to be primarily due to inelastic electron scattering and local fluctuations in ice thickness. This peak is highly variable in amplitude and is routinely filtered out or reduced in traditional single particle analysis. Because of its variability, it cannot be accurately subtracted, and this region is not considered in our analysis. As this peak typically corresponds to periodicities in the specimen of ∼1000 Å, it plays no real role in our analysis of pore structures.

In visually observing vesicles at high magainin concentrations, an interesting observation can be made. Vesicles clearly fall into two classes: some appear smooth, like the magainin-free control experiment, and some appear visibly rough textured. Including both rough- and smooth-appearing vesicles, we have 304 power spectra from individual vesicles in the high-concentration magainin data set. Examining the region from 0.036 to 0.080 Å⁻¹, we observe that the averaged power spectrum exhibits a clear pattern of peaks. However, in looking at the distributions of mean intensity over this range, it becomes clear that separating the data into two populations based on peak height produces one curve with virtually no structure in this region, and another with very strong peaks (Fig. 3 B). Unsurprisingly, when comparing which images fell into each of the two groups, the flat spectrum corresponds to the smooth-looking vesicles, and the power spectrum with peaks corresponds to the images with a rough texture. For purposes of analyzing the observed peak pattern, we will consider the flat curve as the background to produce a new background-subtracted peaked curve (shown in Fig. 4) The difference between ice-only background subtraction and the background subtraction based on weakly perturbed vesicle data is small, but permits significantly better fitting, particularly when CTF is included.

Figure 4.

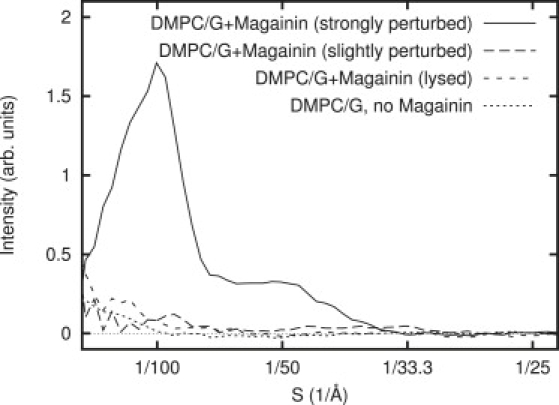
Power spectra of the four classes of vesicles observed: the control without magainin, strongly perturbed vesicles with magainin, slightly perturbed (but not lysed) vesicles with magainin, and lysed vesicles (with magainin). Slightly perturbed and lysed vesicles both clearly exhibit a signal above the control experiment.

Simulation

To permit more precise modeling of possible pore configurations, in addition to the basic two-dimensional hard-disk fluid theory, we also performed simulations. The basic simulation model was a solid spherical shell with pores (Fig. S2 A in the Supporting Material). Technically the pores are conical for simplicity, though this should be a minimal effect given the thinness of the membrane. A control was also simulated with no pores present (Fig. S2 B). The diameter and thickness of the spherical shell in the three-dimensional model were 1056 Å and 46 Å, respectively, but the bilayer was given no internal structure. Since we are limiting ourselves to nearly planar regions of the bilayer, the momentum transfer is almost entirely confined to the plane of the vesicle, so simulating the internal structure of the membrane was deemed unnecessary. Nonoverlapping pores with either a fixed size or a Gaussian size distribution were randomly placed on the surface until the specified density had been achieved. Analysis of these simulated vesicles was performed in the same way as for the experimental data.

CTF correction

In principle, the transmission electron microscope produces images representing two-dimensional projections of the electron density of the object being imaged. However, in actuality, this is not strictly true, as the images also include a number of largely correctable distortions. The functional form of the contrast transfer function (CTF) (40) is regarded as a very accurate representation of the imaging process. In the weak phase approximation, the overall transfer function is written as

$$C\left(q\right)=\sqrt{1-C_{\text{A}}^2}\sin \left(\gamma \right)+C_{\text{A}}\cos \left(\gamma \right),$$ (1)

where

$$\gamma =2\pi \left(-\frac{Cs{\lambda }^3{\left(q/2\pi \right)}^4}{4}+\frac{\Delta Z\lambda {\left(q/2\pi \right)}^2}{2}\right),$$

C_A is the fractional amplitude contrast, C_S is spherical aberration, λ is the electron wavelength, and ΔZ is defocus. In addition, there is an envelope function expressing the falloff in signal at high resolution, which for purposes of our analysis can be approximated as a Gaussian B-factor (41,42) :

$$E\left(q\right)=e^{\frac{-1}{4{\pi }^2}B{q}^2}\text{.}$$

The two most important features of this expression are that C(q) is oscillatory, with a number of zero crossings, and that at typical levels (C_A ∼ 0.1), there is very little contrast close to focus (small ΔZ), but contrast increases further from focus. It is thus standard practice to collect images out of focus to improve contrast. We specifically selected a defocus range such that the first zero crossing of the CTF is at substantially higher resolution (q > 0.25 Å⁻¹) than the region we are analyzing.

The CTF curves are highly dependent on microscope defocus, which is intentionally varied between images. To test for CTF effects, we separated our data by defocus into three groups, without performing any CTF correction. In Fig. 5, we show the averaged power spectra for each of these groups. The lack of significant variation between curves at different defoci demonstrates that defocus is a minor effect with little impact on interpretation. However, although variation with defocus is only a small effect, the presence or absence of the CTF model could have an important impact on interpretation. Therefore, our modeling work incorporates CTF and envelope function terms, using a defocus of 3 μm underfocus and 10% amplitude contrast. Although small changes in these parameters have no significant impact on the fit, omitting the CTF curve entirely causes a measurably worse fit.

Figure 5.

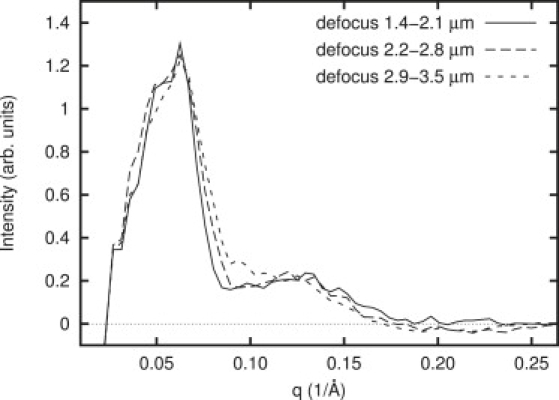
Background-subtracted power spectra of strongly perturbed vesicles grouped by defocus (ΔZ₁ 1.4–2.1 μm; ΔZ₂ 2.2–2.8 μm; and ΔZ₃ 2.9–3.5 μm). Despite the large difference in defocus, no significant peak position shifts occur, implying that our data is not sensitive to the defocus parameter in CTF.

Fitting procedure

The simulated curve, multiplied by the CTF, was used as a model to fit to the experimental data. We used the Levenberg-Marquardt generalized least-squares fitting algorithm (43) to perform fitting. Specific fitting parameters varied and are discussed in Results and Discussion.

Results and Discussion

Qualitative results

In the control experiments, without magainin, vesicles appear smooth, and the bilayer can be clearly observed (Fig. 2 A and Fig. S1). Interestingly, apparent bilayer thickness fluctuations observed around the edge of each vesicle, were substantially stronger than a similar experiment performed with POPC/POPG (POPC/PG) even in the magainin-free control experiment (Fig. S1). Although this relative difference is not entirely unexpected because of the shorter chain-length in the DM membranes, the degree to which the bilayer seems to fluctuate in DMPC/PG membranes is somewhat surprising. Although we cannot make any quantitative statements, it is possible that the fact that POPC/PG responds differently to magainin than DMPC/PG is related to this behavior.

In visually assessing the vesicles in the presence of magainin, they clearly appear to fall into three classes: smooth vesicles (Fig. 2 B, dotted line) similar to those without magainin (Fig. 2 A); highly perturbed vesicles with intact surfaces (Fig. 2 B, solid line); and lysed vesicles with clear discontinuities in their membranes (Fig. 2 C). Furthermore, lysed vesicles may appear directly adjacent to both strongly and weakly perturbed vesicles, and they appear to be, at most, only slightly perturbed. This demonstrates that the magainin-lipid interactions are highly stochastic, and we cannot simply assume that all vesicles will be impacted equally by the presence of magainin. The differentiation of the intact vesicles into two (rough and smooth) classes was not anticipated, but the effect is clear both visually and in terms of the power spectra (Fig. 4). As discussed in Materials and Methods, the weakly perturbed vesicles, as determined by quantitative analysis of the power spectra, were used to compute the background curve for the high-concentration magainin experiments.

A comparison of the power spectra for the four observed vesicle types is shown in Fig. 4:

• 1.The control experiment, with no magainin.
• 2.Vesicles in the presence of magainin exhibiting a strongly perturbed appearance.
• 3.Vesicles in the presence of magainin exhibiting a minimally perturbed appearance.
• 4.Vesicles that had been obviously lysed (containing at least one large gap in the bilayer).

As expected, the strongly perturbed membranes exhibit the strongest scattering peaks in the region of interest. The minimally perturbed vesicles still exhibit stronger scattering than the control experiment, but far weaker than the strongly perturbed class. Additionally, the lysed vesicles agree best with the minimally perturbed category.

Interpretation of power spectra

We now begin by attempting to interpret the data in terms of the model (Fig. 1) assuming a distribution of similar-sized water-filled pores in the bilayer. First we consider a two-dimensional hard-disk fluid model, which can be examined theoretically, but is clearly only a limited approximation of reality.

Theory

Although we are utilizing vesicles in these experiments, which are clearly nonplanar, by using only the central region of each vesicle for purposes of power spectrum calculations (Fig. 2), we are considering two only slightly curved membrane disks, one from the top of the vesicle and one from the bottom. For purposes of theoretical analysis, we consider these slightly curved surfaces to be flat, permitting us to invoke the same scattering theory used to interpret multilayer stack neutron-scattering experiments. This will cause some minor inaccuracies in the structure factor because of packing issues, but is acceptable as a first approximation.

Therefore, in this theoretical analysis, we consider the membrane to be a plane, and the pores to be circular holes in the plane. In the resolution range under consideration, we can consider the electron microscope to produce parallel beam projections of the three-dimensional specimen with corrections for the CTF of the instrument. Additionally, literature has suggested (25) a more complicated potential for pore-pore interactions, but here we consider a simple hard-disk model, with a specified disk radius and pore density to see if that suffices to explain the data. The power spectrum intensity can be expressed as

$$I\left(q\right)={\left|F\left(q\right)\right|}^{2}S\left(q\right),$$

with an additional arbitrary scaling factor. In scattering parlance, the form factor, F(q), is the radial profile of the Fourier transform of a single pore. Since we are modeling each pore as a hard disk, this is simply a Heaviside unit step function u,

$$f\left(r\right)=\frac{1}{\pi R^2}u(R^2-r^2),$$

where R is the radius of the pore and r is spatial coordinate with origin in the middle of pore. We can thus express F(q) as a Bessel function:

$$F\left(q\right)=2\frac{J_1\left(qR\right)}{qR}\text{.}$$

The first maximum after the origin is located at q ≈ 5.14/R. Thus, as expected, the peak moves to the left as the pore size increases.

The structure factor S(q) can be theoretically computed from two-dimensional hard-disk fluid theory (44),

$$S(qR,\eta )=1/\left[1-8\eta {\int }_0^{1}c(r^{\prime },\eta )J_0\left(qR{r}^{\prime }\right)r^{\prime }d{r}^{\prime }\right],$$

where η = (π/4) ρR² is the packing fraction, ρ is the density of pores, c(r′,η) is the direct correlation function, and r′ = r/R is the distance r scaled by the particle diameter R.

The first peak of S(q) is related to the mean distance between particles of the fluid. As the particle density is increased, the peak moves to the right, and increases in intensity. As shown in Fig. 6, in our experiment, the first peak in the power spectrum is thus due primarily to pore density, and the second peak is due primarily to pore size (Fig. S3).

Figure 6.

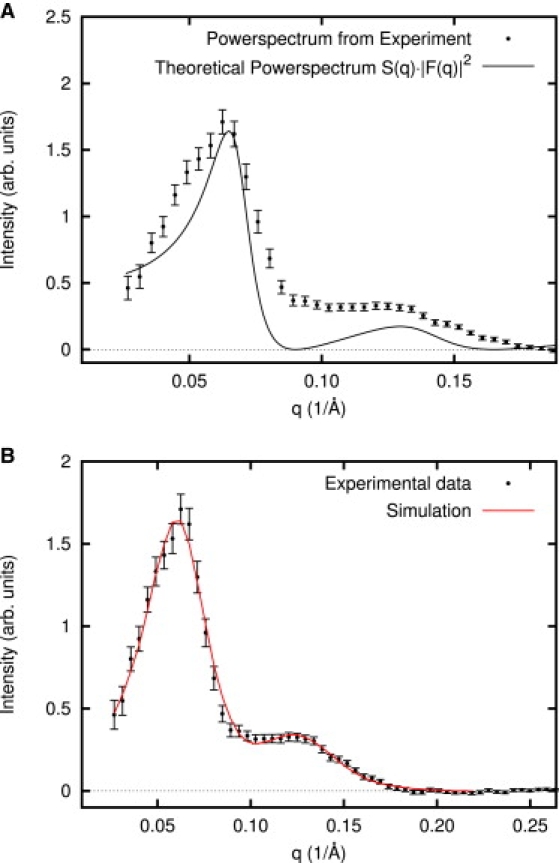
(A) Theoretical analysis of power spectrum of the strongly perturbed vesicles. The solid line is the aggregate theoretical curve including both form (|F(q)|²) and structure (S(q)) factors with pore size and densities optimized to match the experimental data. The pore size deduced from the best theoretical match is ∼83 Å, and the mean distance between pores (center to center) is ∼108 Å. (B) Fitting CTF-corrected simulation curve to the experimental data. Pore size, pore size variation, and pore density are allowed to vary in simulation to yield the best matching power spectra to the experimental data, with CTF correction performed. The best fitting parameter gives a mean pore size of 80 ± 2 Å and the pore size variation 12 Å.

The theoretical curve qualitatively reproduces the main features of the experimental power spectrum, but there are substantial discrepancies between theory and the experimental curve extending well beyond the error bars. However, given the simplicity of the model, we would not have expected an exact fit. A number of obvious possibilities for subtle improvements to the model come to mind, but to test these possibilities we must resort to simulation.

Simulation

One of the most useful aspects of a simulation is that its complexity can be controlled, permitting us to identify the minimal attributes of the problem required to accurately reproduce the data. In this case, a true simulation would include molecular dynamics on all of the molecular components of the experiment. However, before deciding such extremes are useful, we will first begin with our basic hard-disk model and begin adding attributes to it and observe agreement with the data. The details of the simulation are discussed in Materials and Methods, but basically, we begin with a solid spherical shell of specified thickness, then insert random pores. Projections of these simulated vesicles are then treated in the same fashion as the experimental data, including imposition of a simulated CTF. We then permit three parameters to vary, the pore size, the pore density, and the B-factor (see CTF above), and perform a fit. Simply performing the simulation on a spherical section already provides a more accurate description of the problem, as packing on a sphere is different than in a plane, impacting the structure factor. Performing the fit with the simulation provides a much better result than the theory (Fig. S4), but still does not fully model the data.

Additional attributes we could potentially add to the simulation include the structure of the bilayer, explicit peptides, making the edge of the cone soft rather than hard and variations in pore size and/or shape. Given that we observe that the experimental data does not fall to zero between the two peaks, whereas the theoretical curve does, and that the simulation has a deeper dip than the experimental data (Fig. S4), a natural idea would be to try varying the pore size. Indeed, including a Gaussian pore-size variation into the simulation, with the width of the Gaussian as a fourth free parameter produces an excellent fit, without requiring any additional subtleties in the model (Fig. 6 B). Thus, the final fit yields a mean diameter of 80 ± 2 Å, a Gaussian pore size variation of 12 Å, a density of 7.2 × 10⁻⁵ pores/Ų, and an envelope function B factor of 1321 Ų.

We now consider earlier neutron-scattering experiments. No actual neutron scattering was performed for this article, but a brief discussion is useful to make a meaningful comparison with our results. The advantage of neutron scattering over electron or x-ray scattering is that it provides a flexible contrast mechanism, as either the bulk water or various hydrogens in the lipids can be deuterated. In the experiment we are comparing with Ludtke et al. (12), hydrated lipid multilayer stacks are prepared with a known concentration of magainin. The separation between bilayers in the stack is ∼10 Å, so the magainin is effectively entirely associated with the lipid, regardless of charge interactions. Earlier oriented circular dichroism experiments already demonstrated in this environment that above a specific threshold concentration, the peptide oriented itself perpendicular to the surface of the bilayer (11). In the neutron-scattering experiment, the bulk water began as H₂O, then was exchanged for D₂O, then exchanged back to H₂O. In this experiment from Ludtke et al. (11), when the bulk water was H₂O, no signal was observed; but when it was D₂O, two peaks, one large and one small, appeared (Fig. 7, from original data).

Figure 7.

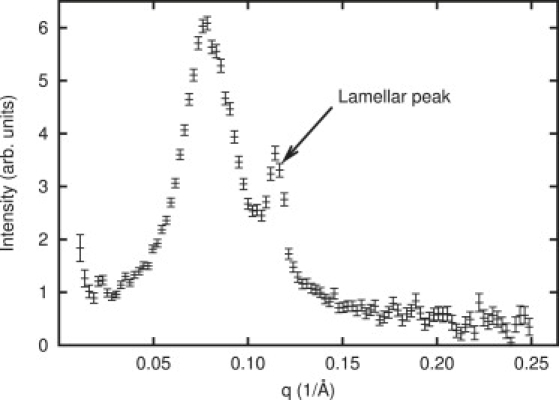
Small angle neutron scattering (SANS) curve from multilayer stacks of DMPC/PG regenerated from original data (12). Multilayer stacks of DMPC/PG showed a pore peak (left peak) yielding a size of ∼71 Å. (Right peak) Residual lamellar scattering peak due to imperfect alignment of the lipid multilayer stacks. Because of differing contrast mechanisms, this curve is not expected to match the electron scattering results directly.

Through an analysis comparable to the one performed here with electron scattering, it was demonstrated that the larger peak was almost certainly due to the presence of water-filled pores in the plane of the bilayers. The smaller peak was due to smectic defects in the multilayer stack structure. Based on this model, the diameter of the water channel was measured as 71 ± 3 Å. Initially, it might seem that the two experiments (neutron and electron scattering) should yield similar values; however, the differences in the source of contrast in the two experiments are quite important. In the neutron-scattering experiment only the column of water filling the actual pore appears, since the magainin and lipid were undeuterated. Only one peak is observed in this experiment, since the channel-channel contact radius is larger than the pore radius, and this produces a falloff in the theoretical scattering curve, which eliminates the second peak observed in the electron scattering experiment. In the electron scattering experiment, we are observing contrast between the lipid bilayer and three possible contrast producing agents:

• 1.The water in the channel.
• 2.The magainin around the edge of the channel.
• 3.If a “wormhole” channel, some portion of the bright phosphate peak lining the edge of the pore.

That is, the contrast-producing mechanism for neutron scattering includes only the pore, whereas in electron scattering it will also likely include some portion of the surrounding pore edge, and could thus be larger. In addition, our simulation required a model where the pore sizes were allowed to vary by ±12 Å for an accurate fit, making the neutron scattering result entirely consistent with this result.

Our simulation-based fit of the data in Fig. 6 B used four parameters, and accurately fit the data to within the limits of measurement uncertainty. However, it is worth considering that this fit determined the B-factor as ∼1300 Ų, rather than the more typical 200–500 Ų for this instrument. In many ways, our simulation model is still oversimplified. Specifically, we are still using pores represented as sharp-edged disks. Softening the edges of the pores would cause an additional decay in the form-factor of the channels, meaning less decay in the Gaussian B-factor would be required to fit the data. That is, with a gradual decay on the edges of the pores, the B-factor would be reduced in the fit. However, given the high accuracy of the current fit, an additional parameter to account for the level of softness in the pore edges would not be separable from the B-factor, and the fit would produce two values with high uncertainty rather than a single well-determined value. The B-factor we are presently determining is a combination of the experimental B-factor from the microscope and the true shape of the edge of the pores, but we do not believe the data permits a more detailed answer without making the results ambiguous.

Conclusions

We have demonstrated clearly that magainin induces surface perturbations in synthetic lipid vesicles, and that these perturbations can be attributed to a random distribution of pores ∼80 Å in diameter, compatible with results from earlier neutron-scattering experiments in multilayer lipid stacks.

Unlike earlier neutron-scattering experiments, the cryo-EM experiments were performed out of equilibrium during the vesicle lysis process. Our results demonstrate that the earlier results in multilayer stacks were not an artifact of that experimental geometry, but can be reproduced in a nativelike situation. This experiment, combined with earlier experiments establishing peptide orientation and leakage, combine to give a clear picture of the biochemistry taking place in this system. When mixed in solution, the magainin first interacts with the outer leaflet of the (charged) vesicles, initially adsorbing to the surface. When the concentration on any specific vesicle surface exceeds a threshold level, the peptide begins inducing wormhole pores, briefly making topological connections between the inner and outer leaflets. The magainin then passes along the topological connection to the inner leaflet. Pores continue to form after magainin equilibrium has been reached between the inner and outer leaflets, but with a much reduced probability, because of both a reduction in surface stress once the peptide has equilibrated and the relative lower concentration of peptide in each leaflet. It is worth mentioning that the argument for wormhole-style pores rather than the traditional barrel-stave pores (Fig. 1) was that in the neutron-scattering experiment, there was an insufficient amount of magainin present to form the lining around the observed pores. The experiment presented here does not offer any new evidence for this particular question, aside from the observation of substantial distortions in membrane thickness already present for DMPC/PG in the absence of magainin.

In some of the vesicles in our experiments, the pore-forming process was sufficient to cause lysis of the vesicle, but as there is no osmotic stress in this synthetic system, it is also quite possible for vesicles to survive this process intact. This model is supported by the fact that the lysed vesicles exhibit a similar pore formation pattern to the less-perturbed looking vesicles, implying that those vesicles are ones that have already achieved equilibration between leaflets. One would expect bacteria to be far less likely to survive the high-density pore-forming phase because of osmotic stress.

We have also demonstrated that cryo-EM can be a powerful tool for studying peptide-lipid interactions even in cases where the resulting structures cannot be individually resolved, and demonstrated that it is straightforward to relate such cryo-EM virtual scattering results to in-plane neutron scattering experiments. One of the major advantages of cryo-EM imaging over a technique like small angle neutron or x-ray scattering is fine control over the portion of the image included in the power spectrum calculation. By computing the power spectrum of only the center of each vesicle, we can effectively perform in-plane scattering, equivalent to a neutron/x-ray scattering experiment, which requires use of lipid multilayer stacks. However, although cryo-EM is an extraordinarily powerful technique, contrast mechanisms are not as flexible as those available in neutron scattering, where deuterium can be used as a very flexible contrast agent with minimal impact on the physical properties of the system. Although there are mechanisms for varying contrast in cryo-EM or x-ray scattering, none are nearly as flexible, and addition of agents such as nanogold labels would have a strongly perturbing effect on systems such as this. This argues for future hybridizations of these independently powerful techniques.

Finally, although we can qualitatively claim that the surface of the perturbed vesicles appears porous, the fact that we are looking through two bilayers, each of which has a high density of pores, makes direct visualization a difficult position to argue. To address this issue and truly visualize individual peptide-induced pores, it will be necessary to move into three dimensions through use of cryo-electron tomography. Although, theoretically, visualizing pores of this size using this technique is possible, there are many complexities, such as the missing-wedge problem, due to the inability to tilt cryo-EM specimens >60–70°. Nonetheless, a successful cryo-electron tomography experiment is clearly the next step in developing cryo-EM as a technique for studying such lipid systems. These same techniques may also offer powerful tools for studying events such as vesicle fusion or the mechanics of membrane-penetrating peptides.

Supporting Material

Four figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)00905-9.