Figure 2.
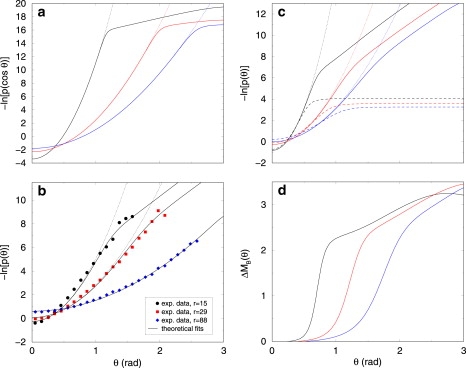
Theoretical predictions of DNA elastic properties in two and three dimensions. (a) Logarithm of the probability distribution p(cos θ) = p(s) in 3D (Eq. 3, solid lines) for different values of r = 5, 15, and 25 bp (from left to right) compared with the WLC model (dotted lines). One bp length is a = 0.34 nm. The Ising and elastic parameter values (in units of kBTR) come from fits to earlier experiments (16): κU = κUB = 147; κB = 5.54; μ = 1.7977; and J = 3.6674. The probability distribution is given by , because ds = sin θ dθ. (b) Logarithm of the probability distributions p(θ) in 2D. Symbols represent experimental data taken from Wiggins et al. (7), whereas the curves are now our best fits, from Eq. 4. The curvilinear distances between monomers in Wiggins et al. (7), namely 5, 10, and 30 nm, correspond, respectively, to r = 15, 29, and 88 bp. The value κB = 5.54 (in units of kBTR) comes from Palmeri et al. (16) and κU = 160.82 comes from fitting the r = 88 bp set of data by a pure WLC model, as in Wiggins et al. (7) (because for such large r, the Gaussian character is restored). The remaining parameters (κUB, J, and μ) are fitted. One possible parameter set is (κUB, J, and μ) = (20.97,1.3173,and 1.6685) (section D in Supporting Material). Dotted lines show the predictions of the WLC model, for comparison. (c) Logarithm of the probability distribution p(θ) in 2D. Parameter values are coming from fits (see panel b), and r = 5, 15, and 25 bp (from top to bottom, solid lines). Dotted line shown the predictions of the WLC model and dashed lines show the same profiles when κB = 0. (d) Average excess chain melting ΔMB(θ) in 2D. Same parameter values as in panel b. From left to right, r = 5, 15, and 25 bp. The elasticity is linear until a threshold , where excessive bending induces bp melting.
