The impact of linac output variations on dose distributions in helical tomotherapy

Abstract

It has been suggested for quality assurance purposes that linac output variations for helical tomotherapy (HT) be within ±2% of the long-term average. Due to cancellation of systematic uncertainty and averaging of random uncertainty over multiple beam directions, relative uncertainties in the dose distribution can be significantly lower than those in linac output. The sensitivity of four HT cases with respect to linac output uncertainties was assessed by scaling both modelled and measured systematic and random linac output uncertainties until a dose uncertainty acceptance criterion failed. The dose uncertainty acceptance criterion required the delivered dose to have at least a 95% chance of being within 2% of the planned dose in all of the voxels in the treatment volume. For a random linac output uncertainty of 5% of the long-term mean, the maximum acceptable amplitude of the modelled, sinusoidal, systematic component of the linac output uncertainty for the four cases was 1.8%. Although the measured linac output variations represented values that were outside of the ±2% tolerance, the acceptance criterion did not fail for any of the four cases until the measured linac output variations were scaled by a factor of almost three. Thus the ±2% tolerance in linac output variations for HT is a more conservative tolerance than necessary.

1. Introduction

1.1. Helical tomotherapy

Helical tomotherapy (HT) is an intensity modulated x-ray therapy (IMXT) modality that is capable of delivering highly conformal dose distributions (Mackie et al 1993, 1999, 2006). Using the Hi-Art™ unit (TomoTherapy, Inc., Madison, WI), radiation is delivered from a 6 MV linear accelerator (linac), with an intensity modulated x-ray fan beam that rotates on a ring-style gantry, while the patient is simultaneously translated into the bore on a treatment couch. The width of the fan beam is controlled by a set of tungsten jaws. The fan beam is divided into beamlets by a binary multileaf collimator (MLC) with 64 leaves, each with a projection at isocenter of 6.25 mm. The intensity of each beamlet is modulated by controlling the amount of time its leaf is open during the 51 angular increments, corresponding to about 7° each, in which the gantry rotation is discretized (Fenwick et al 2004). The ratio of the maximum to the average of all non-zero leaf opening times is restricted in the treatment planning process to be less than or equal to a pre-defined modulation factor, which is usually required to be between unity and five. The distance between windings in the helix is controlled by the pitch, which is defined as the fraction of the field width that the couch translates per gantry rotation. The reciprocal of the pitch is the number of gantry rotations over which a point on the gantry rotation axis in the treatment volume resides inside the primary beam (Fenwick et al 2004, Kissick et al 2005).

1.2. Linac output variations in helical tomotherapy

Throughout the current work it is assumed that the deviation in the HT linac output from the long term mean at a given gantry angle increment is a random variable, sampled from a Gaussian distribution function. The Gaussian distribution function is characterized by its mean and standard deviation, which are referred to as the random and systematic linac output uncertainties, respectively, and are assumed to be functions of gantry angle. The observed linac output variations are assumed to be samplings of the distributions. For convenience, linac output uncertainties will be referred to as percentages of the long-term linac output average, and uncertainties at a point in the spatial dose distribution will be referred to as percentages of the planned dose at that point.

In a set of HT quality assurance (QA) recommendations developed at the University of Wisconsin (Fenwick et al 2004) and based on the QA recommendations for conventional linear accelerators (Kutcher et al 1994) and serial tomotherapy (Low et al 1998a, Low et al 1998b, Woo et al 2003), it is suggested, as monthly check M2, that the rotational linac output stability be within ±2% of the long-term average. To approximate the effects of the linac output variations on the dose distribution, monthly check M3 (Fenwick et al 2004) may also be performed. Check M3 entails averaging the linac output data over a 30 second time window and ensuring that the resulting smoothed data are within ±2% of the long-term average. The 30 second time window is suggested since it is a representative amount of time that a point in the treatment volume would reside inside the aperture defining the primary radiation beam.

The current paper addresses two issues with checks M2 and M3. First, the maximum and minimum of averaged data are always between or equal to the maximum and minimum of the original data, therefore check M3 is redundant if check M2 already passed, and, conversely, passing check M3 does not imply passage for check M2. Second, the validity of check M3 is based on the assumption that all points in the treatment volume receive equal dose contributions from all beams delivered over a 30 second window. As the intensity profiles of individual fan beams are modulated, and the attenuation and scatter of each fan beam in the patient is dependent on the gantry angle, this is not generally the case.

The effects of random and systematic linac output uncertainties on dose distributions are studied by propagating the linac output uncertainties to the dose distributions for four example HT treatment cases. The sensitivity of the dose uncertainty to the linac output uncertainty is assessed by determining the maximum allowable random and systematic linac output uncertainties that would still result in the passage of a dose uncertainty acceptance criterion, which is based on the criterion for acceptance of check M3, but more comprehensive in that the effects of intensity modulation, beam attenuation, and scatter, are accounted for. This approach is used for both modelled and measured linac output uncertainties. It is shown that the acceptance threshold for check M2 could likely be increased above ±2%, as cancellation effects between multiple beam directions tend to reduce the magnitude of the systematic dose uncertainty significantly below the maximum and minimum systematic linac output uncertainty.

2. Materials and Methods

2.1. Dose expression

The dose, d_i, delivered to the voxel indexed by i, can be written as a weighted sum over all of the beamlets that contribute to the dose at that voxel:

$$d_i={\displaystyle \sum _m{\mathrm{\Psi }}_m{\displaystyle \sum _j{D}_{\mathit{\text{ijm}}}{w}_{\mathit{\text{jm}}},}}$$ (1)

where Ψ_m is the intensity at isocenter from the beam delivered over the angular gantry increment indexed by m (m = 1,…,M), which is proportional to the linac output over gantry increment m. The delivery sinogram is represented by w_jm, which is the fraction of time that the MLC leaf indexed by j (j = 1,…,64) is open over angular increment m. D_ijm is the dose per unit intensity at isocenter, or beamlet, delivered to voxel i, corresponding to MLC leaf j of beam m.

2.2. Dose uncertainty

During the treatment planning process, the TomoTherapy TPS calculates the planned dose distribution, $d_i^p$ , by assuming that the linac output intensities, Ψ_m, are always equal to the long term mean intensity, Ψ^p, and assuming perfect models for the dose calculation and sinogram delivery systems. In actuality, Ψ_m, D_ijm, and w_jm are all random variables due to uncertainties in linac output, the dose calculation process, and the MLC leaf opening times, respectively. In the current study, uncertainties in D_ijm and w_jm are neglected, as the TomoTherapy TPS dose calculation systems (Lu et al 2005) and sinogram delivery systems (Balog et al 1999a, Balog et al 1999b) have been well-studied elsewhere. The focus is thus restricted to the propagation of the uncertainty in Ψ_m to the dose distribution.

In the current paper it is assumed that Ψ_m = Ψ^p + ΔΨ_m, where ΔΨ_m is a random variable sampled from a Gaussian distribution with a mean of ${\mu }_m^{\mathrm{\Psi }}$ and a standard deviation of ${\mathrm{\sigma }}_m^{\mathrm{\Psi }}$ . The dose delivered to voxel i can therefore be expressed as $d_i=d_i^p+\mathrm{\Delta }{d}_i$ , where Δd_i is a random variable that is dependent upon ΔΨ_m for all m. Define the systematic and random uncertainties in the dose delivered to voxel i as the mean, ${\mu }_i^d$ and standard deviation, ${\mathrm{\sigma }}_i^d$ , of Δd_i, respectively, which can be obtained using the rules of uncertainty propagation (Bevington 2003) as:

$${\mu }_i^d={\displaystyle \sum _m\frac{\partial (\mathrm{\Delta }{d}_i)}{\partial (\mathrm{\Delta }{\mathrm{\Psi }}_m)}{\mu }_m^{\mathrm{\Psi }}={\displaystyle \sum _m{\mu }_m^{\mathrm{\Psi }}{\displaystyle \sum _j{D}_{\mathit{\text{ijm}}}{w}_{\mathit{\text{jm}}},}}}$$ (2)

and

$${\left({\mathrm{\sigma }}_i^d\right)}^2={\displaystyle \sum _m{\left(\frac{\partial (\mathrm{\Delta }{d}_i)}{\partial (\mathrm{\Delta }{\mathrm{\Psi }}_m)}\right)}^2{\left({\mathrm{\sigma }}_m^{\mathrm{\Psi }}\right)}^2={\displaystyle \sum _m{\left({\displaystyle \sum _j{D}_{\mathit{\text{ijm}}}{w}_{\mathit{\text{jm}}}}\right)}^2{\left({\mathrm{\sigma }}_m^{\mathrm{\Psi }}\right)}^2.}}$$ (3)

As Δd_i is a linear combination of the Gaussian-distributed random variables, Ψ_m, for all m, it follows that Δd_i is also a Gaussian-distributed random variable (Larson and Marx 2001).

2.3. Cases and treatment planning

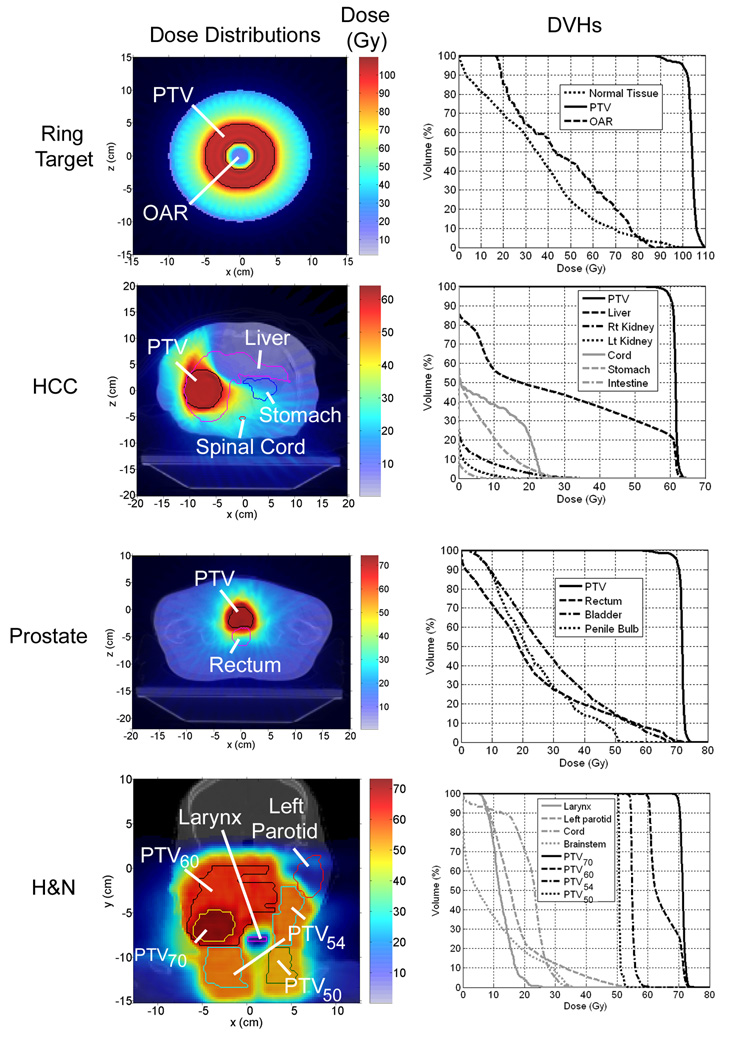
One idealized case and three clinical cases were considered for study. The idealized case, or ring target case, consisted of a ring-shaped dose prescription in a simulated cylindrical phantom with both radius and height of 10 cm. The prescription region had a height of 5 cm, with an annular transverse cross section of 2 cm inner radius and 5 cm outer radius. The ring target case was chosen to represent a symmetric dose distribution with a central avoidance region. The treatment couch was neglected for the ring target in order to ensure that the fan beam intensity profiles would be nearly constant for all delivery angles.

The three clinical cases were a hepatocellular carcinoma (HCC) case, a prostate case, and a head and neck (H&N) case. The clinical cases were chosen to represent three delivery situations: an off-centre tumour (HCC), a centralized tumour with adjacent avoidance regions (prostate), and a complex situation with multiple planning target volumes (PTVs) and multiple avoidance regions (H&N). The prescription for the HCC case required that 95% of the PTV receive 60 Gy or higher, and the kidneys, spinal cord, stomach, intestine, and liver were all considered avoidance structures. For the prostate case, 95% of the PTV was required to receive 70 Gy or higher, and the rectal wall, bladder, and penile bulb were considered avoidance structures. The H&N case had the most complex prescription, with four PTVs, each of which was subscripted with the dose in Gy that was prescribed to 95% of its volume: PTV₇₀, PTV₆₀, PTV₅₄, and PTV₅₀. PTV₇₀ was the gross tumour volume (GTV) on the right hand side of the patient, and was surrounded by PTV₆₀, which contained regional lymph nodes. PTV₅₄ contained both supraclavicular lymph nodes contralateral to the GTV and subclavicular lymph nodes ipsilateral to the tumour. PTV₅₀ contained subclavicular nodes contralateral to the tumour. Avoidance structures for the H&N case included the spinal cord, larynx, brainstem, left parotid, and oral cavity.

All beamlet (D_ijm) calculations were done on a 2.35×2.35×3 mm³ grid of voxels for all cases. Since the commercial TomoTherapy treatment planning system (TPS) does not provide the user with individual beamlets in an easily accessible format, D_ijm calculations for each case were done with a non-commissioned, in-house, convolution superposition algorithm. The in-house convolution superposition algorithm calculates dose distributions based on CT scans in a similar manner as the algorithm used by the TomoTherapy TPS (Lu et al 2005), using polyenergetic energy deposition kernels (Hoban et al 1994) based on monoenergetic kernels (Mackie et al 1988). Delivery sinograms for each case were obtained by minimizing a quadratic objective function of the same form as that used by the commercial TomoTherapy treatment planning system using 500 iterations of the linear least squares method (Shepard et al 2000). Although not suitable for clinical treatment planning, dose distributions calculated from the code were suitable for the current study, as the analysis focused on the relative effects of linac output uncertainty on the dose distributions rather than the accuracy of the dose calculation itself.

A list of the delivery and optimization parameters for each case is shown in table 1. Images of the planned dose distributions and cumulative dose volume histograms (DVHs) for all of the optimized plans are shown in the first and second columns of figure 1, respectively.

Table 1.

Delivery and optimization parameters for treatment plans.

Case	Actual Modulation Factor	Field Width (cm)	Pitch (rot−1)	Structure	Criterion	Weight
Ring target	3.0	2.5	0.216	PTV	Uniform dose = 100 Gy	100
				OAR	Max dose = 20 Gy	1
				Normal tissue	Max dose = 10 Gy	1
HCC	3.0	2.5	0.216	PTV	Uniform dose = 60 Gy	100
				Liver minus	Max DVH: 10 Gy to 35%	80
				PTV	Max dose = 50 Gy	30
				Spinal cord	Max dose = 22.8 Gy	40
					Max DVH: 20 Gy to 10%	1
				Stomach	Max dose = 30 Gy	6
					Max DVH: 19.2 Gy to 50%	1
				Kidneys	Max DVH: 5 Gy to 5%	1
				Intestine	Max DVH: 19.2 Gy to 50%	1
					Max dose = 30 Gy	1
Prostate	3.0	2.5	0.216	PTV	Uniform dose = 70 Gy	1200
				Bladder	Max DVH: 30 Gy to 30%	200
					Max dose = 60 Gy	10
				Rectal wall	Max DVH: 20 Gy to 35%	100
					Max dose = 60 Gy	10
				Unspecific	Max DVH: 10 Gy to 10%	3
				normal tissue	Max dose = 70 Gy	1
Head and Neck	3.3	2.5	0.172	PTV70	Min dose = 70 Gy	100
					Max dose = 70 Gy	5
				PTV60	Min dose = 60 Gy	100
					Max dose = 60 Gy	5
				PTV54	Min dose = 54 Gy	100
					Max dose = 54 Gy	5
				PTV50	Min dose = 50 Gy	20
					Max dose = 50 Gy	5
				Spinal cord	Max DVH: 25 Gy to 25%	10
					Max dose = 35 Gy	10
				Larynx	Max DVH: 20 Gy to 15%	10
					Max dose = 20 Gy	10
				Brainstem	Max DVH: 25 Gy to 20%	10
					Max dose = 35 Gy	5
				Left Parotid	Max DVH: 20 Gy to 20%	5
					Max dose = 54 Gy	5
				Oral cavity	Max dose = 40 Gy	5
					Max DVH: 20 Gy to 30%	2

Figure 1.

Left column: planned dose distributions. Axial images are shown for ring target, HCC, and prostate cases. A coronal image is shown for the H&N case. Right column: cumulative DVHs corresponding to the dose distribution in the same row.

2.4. Dose uncertainty acceptance criterion

Since the dose variation in voxel i, Δd_i, is assumed to be a Gaussian-distributed random variable with mean μ_i and standard deviation σ_i, the probability, P, that Δd_i is within some fraction, α, of the planned dose, can be calculated as follows:

$$P(-\alpha d_i^p\le \mathrm{\Delta }{d}_i\le \alpha d_i^p)={\displaystyle \underset{-\alpha d_i^p}{\overset{\alpha d_i^p}{\int }}\frac{\mathit{dx}}{\sqrt{2\pi }{\mathrm{\sigma }}_i^d}\text{exp}\left[-\frac{1}{2}{\left(\frac{x-{\mu }_i^d}{{\mathrm{\sigma }}_i^d}\right)}^2\right] .}$$ (4)

Define η_i as the binary dose uncertainty acceptance variable for voxel i:

$${\eta }_i=\{\begin{array}{cc}\hfill 1\hfill & \hfill \text{if}P(-\alpha d_i^p\le \mathrm{\Delta }{d}_i\le \alpha d_i^p)\ge P_{\mathit{\text{accept}}}\hfill \\ \hfill 0,\hfill & \hfill \text{else},\hfill \end{array}$$ (5)

where P_accept is the minimum acceptable probability that the delivered dose is within a ±α fraction of the planned dose. An η_i value of zero represents a fail, whereas a value of unity represents a pass.

The dose uncertainty acceptance criterion is satisfied if equation 5 is satisfied for all of the voxels in the PTV, for an α value of 2% and a P_accept value of 95%. This acceptance criterion is based on the HT QA requirement M3 (Fenwick et al (2004)), but it is more comprehensive in that the dose uncertainties in all voxels in the PTV are considered, and the beamlets (D_ijm) and delivery sinogram (w_jm) are directly used in the uncertainty propagation. Thus the non-uniform fan beam intensity profiles, beam attenuation, and scatter in the patient are accounted for.

Since approximately 95% of the area under a Gaussian curve is within two standard deviations from the mean, equation 5 can be simplified for a P_accept of 95% to:

$${\eta }_i=\{\begin{array}{cc}\hfill 1\hfill & \hfill \text{if}\left|{\mu }_i^d\right|+2{\mathrm{\sigma }}_i^d\le \alpha d_i^p\hfill \\ \hfill 0.\hfill & \hfill \text{else}.\hfill \end{array}$$ (6)

The effects of random and systematic linac output uncertainties on dose distributions were investigated by determining how great ${\mu }_m^{\mathrm{\Psi }}$ and ${\mathrm{\sigma }}_m^{\mathrm{\Psi }}$ can become before the dose uncertainty acceptance criterion failed to be satisfied for each case described in section 2.3. The analysis was performed for both modelled and measured versions of ${\mu }_m^{\mathrm{\Psi }}$ and ${\mathrm{\sigma }}_m^{\mathrm{\Psi }}$ .

2.5. Modelled linac output uncertainties

Since the Hi-Art™ linac output as a function of gantry angle is known to be sinusoidal in shape (Fenwick et al 2004), a cosine function was used to model ${\mu }_m^{\mathrm{\Psi }}$ :

$${\mu }_{m,\text{mod}}^{\mathrm{\Psi }}={\mathrm{\Psi }}^{p}A\text{cos}\left(2\pi f\frac{m}{51}\right).$$ (7)

The frequency, f, represented the number of oscillations in ${\mu }_{m,\text{mod}}^{\mathrm{\Psi }}$ per gantry rotation, and A was the amplitude of the oscillations expressed as a fraction of the planned output intensity, Ψ^p. ${\mathrm{\sigma }}_m^{\mathrm{\Psi }}$ was modelled as:

$${\mathrm{\sigma }}_{m,\text{mod}}^{\mathrm{\Psi }}={\mathrm{\Psi }}^p\beta ,$$ (8)

where 0 ≤ β.

The effects of the modelled linac output uncertainties on each of four cases shown in figure 1 were investigated by finding the maximum acceptable amplitude, i.e., the lowest A (0 ≤ Α) such that the dose uncertainty acceptance criterion was violated. This test was performed for frequency parameters in equation 7 varying between 0.5 and 10 rot⁻¹ in increments of 0.5 rot⁻¹, and for β values between 0% and 5% in increments of 1%.

2.6. Measured linac output uncertainties

Linac output variation measurements were obtained by accessing Hi-Art™ monitor chamber data from a Hi-Art™ machine at the University of Wisconsin, as suggested by Fenwick et al (2004). A data set was chosen that represented an actual scenario in which the linac output variations were outside of the ±2% tolerance required by check M2. The variations returned to acceptable levels of around ±1% after linac servicing.

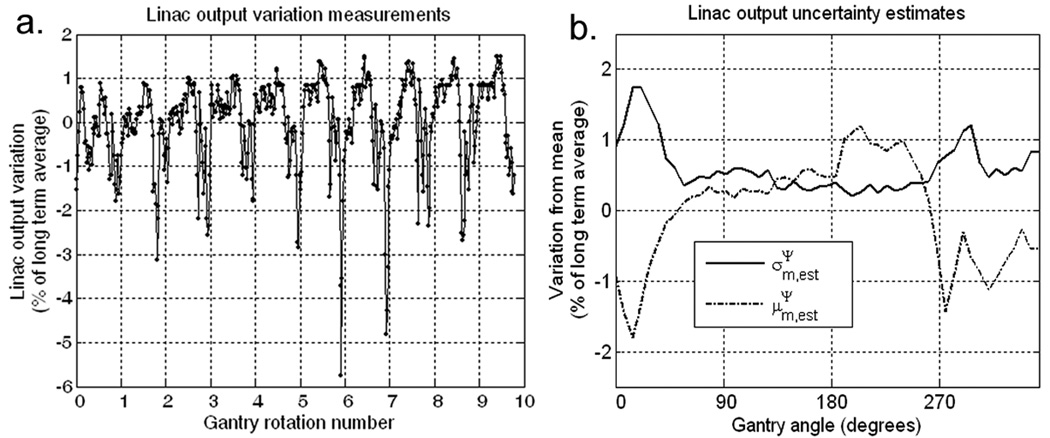
The monitor chamber data were acquired while the gantry underwent ten rotations with a period of 20 s. During the measurement process, the number of linac pulses per second (trigger rate) was 300 Hz, the monitor unit (MU) rate was 800 MU/min, the pitch was zero, and the jaw width was 2.45 cm at isocenter. The monitor chamber was read out at a rate of 30 Hz, therefore each measurement represented the monitor chamber charge accumulated over approximately 10 linac pulses. The monitor chamber charge, χ_m,k, collected in angular increment m (m=1,…,51), of gantry rotation k (k=1,…,10), was obtained by binning the raw monitor chamber charge data into fifty-one 7.06° angular bins for each rotation, each corresponding to one angular increment in the delivery sinogram. About twelve raw monitor chamber measurements were acquired for each angular bin (30 Hz times 20 s per rotation divided by 51 gantry angle increments per rotation). The linac output intensity, ψ_m,k, for gantry angle increment m, and rotation, k, could be obtained by multiplying χ_m,k by ψ͘, the beam intensity per unit monitor chamber charge.

The estimated long term average of the linac output, ${\mathrm{\Psi }}_{\mathit{\text{est}}}^p$ , was obtained by averaging ψ_m,k over all k and m. The measured linac output variations, Δψ_m,k, were calculated as: $\mathrm{\Delta }{\psi }_{m,k}={\psi }_{m,k}-{\mathrm{\Psi }}_{\mathit{\text{est}}}^p$ . A plot of the fluctuations of Δψ_m,k as a percentage of ${\mathrm{\Psi }}_{\mathit{\text{est}}}^p$ is shown in figure 2a. The estimated systematic, ${\mu }_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ , and random, ${\mathrm{\sigma }}_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ , uncertainties in the linac output were obtained by calculating the mean and the standard deviation of Δψ_m,k, over all k, as follows:

$${\mu }_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}=\frac{1}{10}{\displaystyle \sum _{k=1}^{10}\mathrm{\Delta }{\psi }_{m,k},}{\left({\mathrm{\sigma }}_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}\right)}^2=\frac{1}{9}{\displaystyle \sum _{k=1}^{10}{\left(\mathrm{\Delta }{\psi }_{m,k}-{\mu }_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}\right)}^2,m=1,\dots ,51.}$$ (9)

Figure 2.

(a) Linac output variation data, Δψ_m,k, obtained from pulse-by-pulse monitor chamber data acquired over ten HT gantry rotations. Each point represents the sum of all of the output pulses acquired over a single gantry angle increment of about 7°. (b) Random and systematic linac output uncertainty estimated from the data in (a). All data are expressed as a percentage of the long term average measured linac output.

Plots of ${\mu }_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ and ${\mathrm{\sigma }}_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ are shown in figure 2b, which were propagated to the dose distributions for all four cases by assuming ${\mu }_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ and ${\mathrm{\sigma }}_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ exhibited periodicity with a period of 51 with respect to the gantry angle index, m. In order to determine the highest acceptable magnitude for the linac output variation data, ${\mu }_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ and ${\mathrm{\sigma }}_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ were scaled for all four cases described in section 2.3 until the dose acceptance criterion failed. The exact value of ψ͘ need not be known for the uncertainty propagation analysis. This is because $d_i^p,{\mu }_i^d$ , and ${\mathrm{\sigma }}_i^d$ are all proportional to ψ͘, thus equation 6 is independent of ψ͘.

3. Results and Discussion

3.1. Acceptance tolerances for modelled systematic and random uncertainties

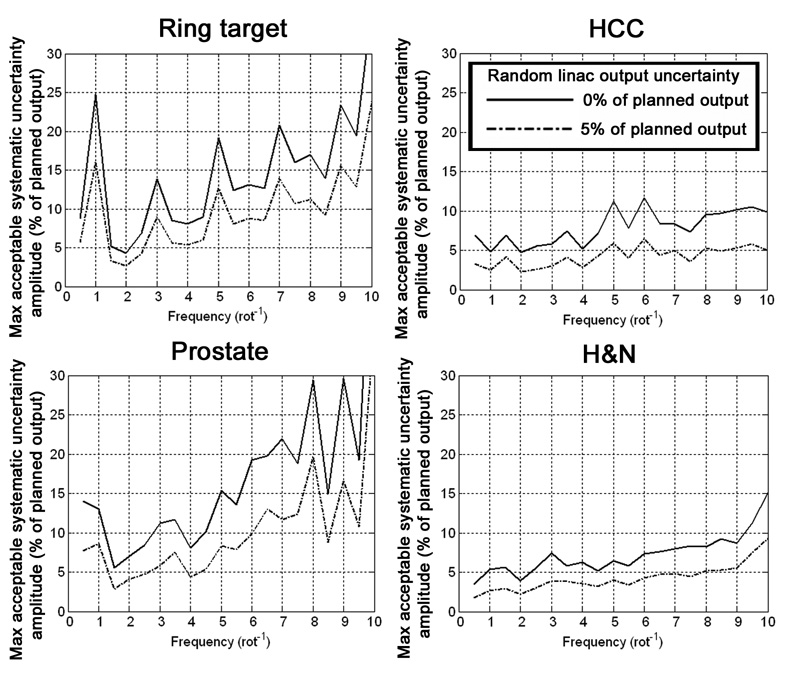
Using the terminology in section 2.5, the maximum acceptable A values as a function of f, for β values of 0% and 5%, are shown for all four cases in figure 3. Higher curves represent plans that are less sensitive to random and systematic linac output uncertainties. The f and A values corresponding to the most (f_worst, A_worst) and least (f_best, A_best) sensitive systematic linac output uncertainty situations for β values of 0% and 5% are listed table 2.

Figure 3.

Tolerances for sinusoidal systematic uncertainty amplitudes. Higher curves represent a lower sensitivity to systematic uncertainties.

Table 2.

Summary of the most sensitive systematic linac output uncertainty frequencies and corresponding amplitudes (f_worst and A_worst, respectively), and the least sensitive frequencies and corresponding amplitudes (f_best and A_best, respectively). Data for random linac output uncertainties of 0% and 5% of the long-term linac output are listed.

	β = 0%				β = 5%
	fworst (rot−1)	Aworst (%)	fbest (rot−1)	Abest (%)	fworst (rot−1)	Aworst (%)	fbest (rot−1)	Abest (%)
Ring target	2.0	4.3	10.0	35.3	2.0	2.7	10.0	23.8
HCC	2.0	4.7	6.0	11.7	2.0	2.3	6.0	6.4
Prostate	1.5	5.5	10.0	56.8	1.5	2.8	10.0	36.6
H&N	0.5	3.5	10.0	15.2	0.5	1.8	10.0	9.3

For all four cases, the ratio of ${\mathrm{\sigma }}_i^d$ to $d_i^p$ in the voxels in the PTV was lower than the ratio of ${\mathrm{\sigma }}_m^{\mathrm{\Psi }}$ to Ψ^p by about a factor of $1/\sqrt{N}$ (data not shown), where N was the number of beams affecting the voxel, approximately equal to 51/pitch. This was expected, as random uncertainties propagate in quadrature.

The plot for the ring target case in figure 3 is useful for developing intuition regarding the behaviour of ${\mu }_i^d$ as a function of the parameters f and A. This is because the radial symmetry of the cylindrical phantom and dose prescription about the isocenter resulted in similar intensity profiles for all beams that affected the PTV, making the analysis straightforward. When f is an even integer, the ${\mu }_{m,\text{mod}}^{\mathrm{\Psi }}$ values for two beams that oppose each other have the same sign and values, and therefore do not cancel each other. When f is an odd integer, the ${\mu }_{m,\text{mod}}^{\mathrm{\Psi }}$ values for opposing beams have opposite signs and values, therefore there is some cancellation between the two beams, resulting in spikes in acceptable A values for odd f, as shown in figure 3. In addition, cancellation is more likely to occur at points that are affected by a relatively high number of beams, as single or opposing beams do not dominate the ${\mu }_i^d$ calculation at those points. For the ring target case, the voxels that caused the dose uncertainty acceptance criterion to fail first for all f lay on the PTV-side of the interface between the PTV and the OAR. These voxels were affected by a relatively low number of beams due to their close proximity to the OAR, and therefore were more sensitive to increases in A.

Since patients are never radially symmetric, the simple intuitive arguments that hold for the ring target case no longer apply, and ${\mu }_i^d$ becomes more difficult to interpret. In the plots for the clinical cases in figure 3 the behaviour of the maximum acceptable A is a complicated function of f, and a trend of spikes at the odd values of f is not evident, except for the prostate case, which is due to the central location and approximate cylindrical shape of the prostate. The curves in figure 3 for the HCC and H&N cases were lower than those for the prostate case due to the presence of PTVs that were off-centre. The relatively low number of beams and the lack of symmetry in the beam intensities affecting the voxels near the outer peripheries of the off-centre PTVs made cancellation of systematic dose uncertainties from multiple beam directions less likely in those voxels, making them the first to cause the failure of the dose uncertainty acceptance criterion.

Assuming that the maximum allowable A value for any given case is represented by the worst-case scenario, A_worst, the corresponding amplitudes for the ring target, HCC, prostate, and H&N cases were 4.3%, 4.7%, 5.5%, and 3.5%, respectively, for a β value of 0%, and 2.7%, 2.3%, 2.8%, and 1.8%, respectively, for a β value of 5%. For each f, the A_worst values corresponding to β values from 1% and 4% decreased linearly between those for β values of 0% and 5%. For all four cases, the A_worst values occurred at frequencies of 2.0 rot⁻¹ or below, which are representative of systematic linac output uncertainty frequencies that occur in practice (Fenwick et al 2004).

Dose acceptance curves for an arbitrary α value (α > 0), α_new, in the dose uncertainty acceptance criterion can be obtained by scaling the curves in the left hand column of figure 3 by α_new/2%. This follows from the linearity of the binary voxel-based dose uncertainty acceptance criterion in equation 6.

3.2. Uncertainty propagation analysis for measured output variations

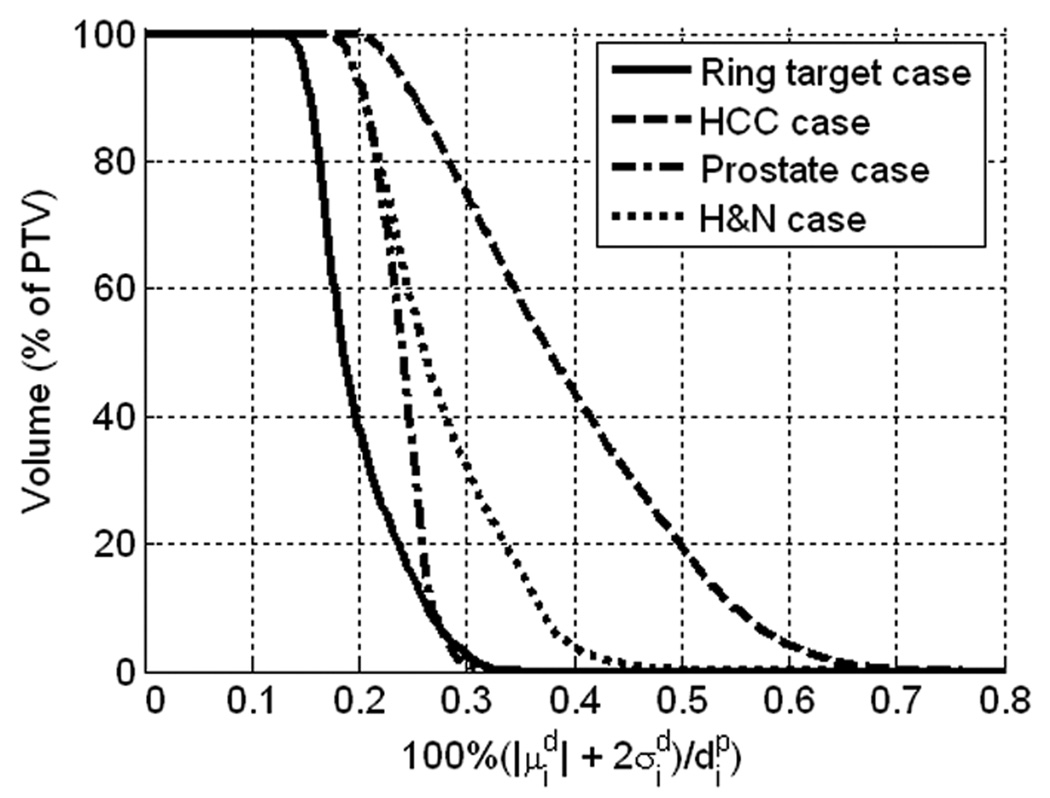
In order to quantitatively display the dose uncertainties corresponding to the measured output variations, cumulative uncertainty volume histograms (UVHs) are shown for all four cases in figure 4. The cumulative UVH is defined as:

$$\text{UVH}(x)=\text{percentage}\text{of}\text{voxels}\text{in}\text{volume},V,\text{such}\text{that}x\le \frac{\left|{\mu }_i^d\right|+2{\mathrm{\sigma }}_i^d}{d_i^p}·100\%,$$ (10)

which is similar to the definition of the cumulative DVH (Niemierko and Goitein 1991), except that dose is not the quantity of interest in the volume. The distribution of $\left(\right|{\mu }_i^d|+2{\mathrm{\sigma }}_i^p)/d_i^p$ in the PTV of each case is relevant due to its direct relationship to the binary dose uncertainty acceptance criterion (equation 6). Each UVH in figure 4 is based on the PTV of the corresponding case, and the PTV for the H&N case was the union of the PTV₅₀, PTV₅₄, PTV₆₀, and PTV₇₀ regions.

Figure 4.

Uncertainty volume histograms (UVHs) for the quantity 100%· $\left(\right|{\mu }_i^d|+2{\mathrm{\sigma }}_i^d)/d_i^p$ , estimated from the HT linac output measurements, for voxel indices, i, in the PTV for each case. The PTV for the H&N case was taken to be the union of PTV₅₀, PTV₅₄, PTV₆₀, and PTV₇₀.

The UVH plots in figure 4 show that the $\left(\right|{\mu }_i^d|+2{\mathrm{\sigma }}_i^p)/d_i^p$ values for the linac output variations in figure 2b were between zero and 0.8% for all four cases, and therefore the dose uncertainty acceptance criterion passed for all cases. The scaling of the measured output uncertainties required such that the dose uncertainties failed to satisfy the dose uncertainty acceptance criterion for the ring target, HCC, prostate, and H&N cases were 6.6, 2.9, 8.4, and 3.4, respectively. As the plot of measured linac output variations shown in figure 2a contains points that are outside of the acceptance threshold for check M2, this suggests that the tolerance of ±2% is more conservative than necessary in practice.

3.3. Relationship between modelled and measured linac output uncertainties

A crude estimate for the scaling factor for the measured uncertainties that will result in the failure of the dose uncertainty acceptance criterion can be calculated using data from the cases of the modelled linac output uncertainties. By taking a conservative approach in which it is assumed that A_worst for an arbitrary case is modelled as a function of β using the data from the H&N case, which was the worst-case-scenario for the cases of modelled linac output uncertainties examined in the current work, A_worst can be expressed as a function of β as:

$$\begin{array}{cc}{A}_{\mathit{\text{worst}}}(\beta )& =A_{\mathit{\text{worst}}}^{H\&N}{|}_{\beta =5\%}+\left(A_{\mathit{\text{worst}}}^{H\&N}{|}_{\beta =0\%}-A_{\mathit{\text{worst}}}^{H\&N}{|}_{\beta =5\%}\right)\frac{5-\beta }{5},0\le \beta \le 5\%\\ & =1.8+(3.5-1.8)\frac{5-\beta }{5}\ge 0.34(10-\beta ),0\le \beta \le 5\%,\hfill \end{array}$$ (11)

where the $A_{\mathit{\text{worst}}}^{H\&N}{|}_{\beta =0\%}$ and $A_{\mathit{\text{worst}}}^{H\&N}{|}_{\beta =5\%}$ data were taken from table 2. Assume now, referring to figure 2b, that ${\mu }_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ can be approximately represented as a cosine function, shifted by −180°, with an amplitude to 1.5%, and the ${\mathrm{\sigma }}_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ data can be represented by their average over all gantry angles, which is 0.6%. An estimate of the maximum allowable scaling factor for the measured data, a, can be calculated by substituting 1.5a and 0.6a for A_worst and β, respectively, in equation 11, and solving for a. This process yields an a of 2.0, which is less than the lowest acceptable scaling value for the measured data, which was 2.9 for the HCC case, and therefore a safe estimate.

3.4. A simple check for the acceptability of linac output variations

A simple check for assessing the acceptability of a set of linac output variations is to associate the maximum of ${\mu }_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}/{\mathrm{\Psi }}^p$ (m = 1,…,51), with a sinusoidal amplitude, A_est. Conservatively assuming that ${\mu }_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ has a frequency of f_worst (although ${\mu }_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ may have sinusoidal components of multiple different frequencies), a worst-case value of β can be derived from equation 11 by letting A_worst = A_est and then solving for β. The check fails if the average value of ${\mathrm{\sigma }}_{m,\mathit{\text{est}}}^{\mathrm{\Psi }}$ is greater than β, and linac servicing will be required.

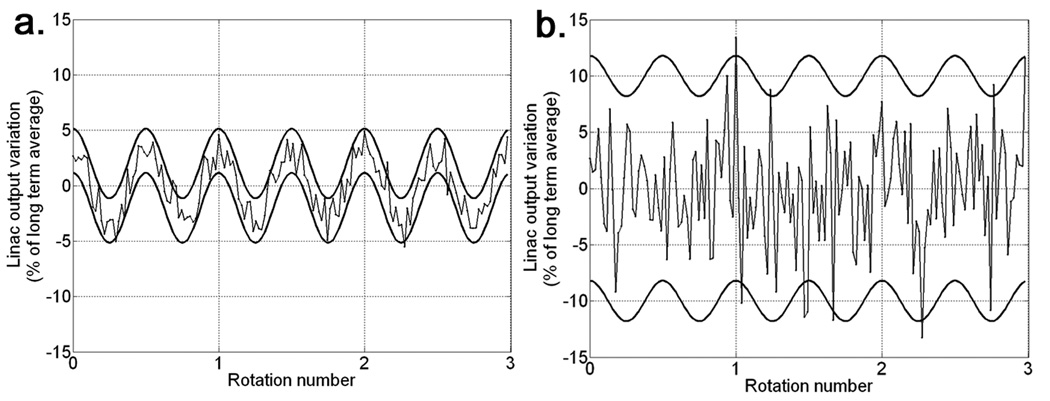
Two examples of simulated linac output variations that are on the borderline of failing the check are shown for three gantry rotations in figure 5. Figure 5a shows output variations that were sampled at each gantry angle increment from a Gaussian function with mean given by equation 7, with f = 2.0 and A = 3.06%, and standard deviation given by equation 8, with β = 1%. Figure 5b shows output variations that were sampled in the same way as those in figure 5a, except that A = 1.8% and β = 5%. The A and β parameters used for figures 5a and 5b satisfy equation 11. Both of these linac output variation plots have many points that are above the ±2% tolerance of check M2, but the corresponding dose uncertainties are sufficiently low to satisfy the dose uncertainty acceptance criterion.

Figure 5.

(a) Upper and lower thick curves represent the sinusoidal, systematic, linac output uncertainty, ${\mu }_{m,\text{mod}}^{\mathrm{\Psi }}$ (f = 2 rot⁻¹, A = 3.06%), plus and minus two standard deviations of the modelled random linac output uncertainty, ${\mathrm{\sigma }}_{m,\text{mod}}^{\mathrm{\Psi }}$ (β = 1%) , respectively. The thin curves represent an example set of realized output variations, ΔΨ_m, for m=1,…,153 (3 gantry rotations), sampled at each m from a Gaussian distribution with mean ${\mu }_{m,\text{mod}}^{\mathrm{\Psi }}$ and standard deviation of ${\mathrm{\sigma }}_{m,\text{mod}}^{\mathrm{\Psi }}$ . (b) Same as (a), except that A = 1.8% and β = 5%. All curves are expressed as percentages of the long term average linac output intensity, Ψ^p.

4. Conclusions

Assuming the long-term mean linac output matches the planned value, sinusoidal systematic linac output uncertainties tend to cancel when propagated to the dose distribution, and random dose uncertainties in voxels in the PTV were reduced relative to random linac output uncertainties by about a factor of $1/\sqrt{N}$ , where N = 51/pitch was the number of HT beams affecting the voxel.

The ±2% linac output variation threshold for passage of check M2 was shown to be overly conservative, as, for all four cases, the dose uncertainty acceptance criterion was satisfied for modelled sinusoidal systematic and random linac output uncertainties of 1.8% and 5%, respectively, which resulted in linac output variations that were well above 5%, as shown in figure 5b. This point was demonstrated for measured linac output variations also, as variations that failed to pass check M2 only failed to satisfy the dose uncertainty acceptance criterion for one of the cases after being scaled by a factor of around three.

All four cases were most sensitive to sinusoidal systematic linac output uncertainties with frequencies of 2 rot⁻¹ or less, which are representative of the frequencies that occur in practice. Although the prostate and ring target cases satisfied the dose uncertainty acceptance criterion for sinusoidal systematic linac output uncertainties with amplitudes above 20%, such high amplitudes should never be allowed in practice, as cancellation of the corresponding systematic linac output uncertainty will only occur in fortuitous cases. A new output variation check has therefore been suggested that is based on the worst-case findings of the modelled systematic linac output uncertainty.