Power Computations for Intervention Analysis

Abstract

In many intervention analysis applications, time series data may be expensive or otherwise difficult to collect. In this case the power function is helpful, because it can be used to determine the probability that a proposed intervention analysis application will detect a meaningful change. Assuming that an underlying autoregressive integrated moving average (ARIMA) or fractional ARIMA model is known or can be estimated from the preintervention time series, the methodology for computing the required power function is developed for pulse, step, and ramp interventions with ARIMA and fractional ARIMA errors. Convenient formulas for computing the power function for important special cases are given. Illustrative applications in traffic safety and environmental impact assessment are discussed.

1. INTRODUCTION

Intervention analysis developed by Box and Tiao (1976a) has been widely used in a variety of applications in engineering, biological, environmental, and social sciences to quantify the effect of a known intervention at time t = T on data collected as a time series, z_t, t = 1,…, n. In its simplest form, intervention analysis itself may be regarded as a generalization of the two-sample problem to the case where the error or noise term is autocorrelated. It is well known that the usual two-sample procedures are not robust against alternatives involving autocorrelation (Box, Hunter, and Hunter 1978, sec. 3.1). The purpose of this article is to describe methods for computing the sample size necessary to detect an intervention with a prescribed power and level. It is shown by simulation experiments that these methods can be accurate even in moderately small samples. Statistical power computations have also been studied by Tiao et al. (1990) and Weatherhead et al. (1998) for particular types of intervention analysis models used for trend detection with environmental time series. The present article extends and refines these results.

It is assumed that for t < T + b, where b is the delay parameter, the time series is generated by a fractional autoregressive integrated moving average model, ARIMA(p, d, q) with fractional differencing parameter | f | < .5. Stationary short-memory time series models, d = f = 0, are used in environmental impact assessment (Box and Tiao 1976a; Tiao et al. 1990; Noakes and Campbell 1992; Weatherhead et al. 1998; Hipel and McLeod 1994, sec. 19.4.5) and in quality control (Jiang, Tsui, and Woodall 2000), as well as in many other areas of science and technology. Nonstationary models with d = 1 and/or long-memory models with 0 < f < .5 have numerous applications in the physical and engineering sciences, such as quality control and industrial time series (Luceño 1995; Box and Luceño 1997), Internet traffic (Cao, Cleveland, Lin, and Sun 2001), daily solar irradiance (Kärner 2002), levels of Lake Huron (Roberts 1991, pp. 319–320), daily wind speed (Haslett and Raftery 1989), and various types of hydrologic time series (Beran 1994; Hipel and McLeod 1994).

In general, we may write the fractional ARIMA model for the preintervention series as

$${\nabla }^{d+f}{z}_t=\xi +\theta (B)/\phi (B)a_t,t=1,\dots ,T+b-1,$$ (1)

where ξ is the constant term, d is the differencing parameter, ∇ = 1 − B, θ (B) = 1 − θ₁B − ··· − θ_qB^q, φ (B) = 1 − f₁B − ··· − φ_pB^p, and B is the backshift operator on t. The innovations, denoted by a_t, t = 1,…, n, are assumed to be independent and normally distributed with mean 0 and variance ${\sigma }_{\mathbf{a}}^2$. It is also assumed that φ (B) = 0 and θ (B) = 0 have no common roots and that all roots are outside the unit circle.

2. SIMPLE INTERVENTION ANALYSIS MODEL

2.1 Introduction

The simple intervention analysis (SIA) model may be written as

$${\nabla }^d{z}_t=\xi +\omega {\nabla }^d{B}^b{I}_t^{(T)}+{\nabla }^{-f}\frac{\theta (B)}{\phi (B)}{a}_t,t=1,\dots ,n,$$ (2)

Where $I_t^{(T)}$ is the intervention series, ω is the parameter indicating the magnitude of the intervention, and ∇^−f θ(B)/φ(B)a_t is the stationary error component. In this article three types of intervention series are used, the step, pulse, and ramp series, defined by

$$I_t^{(T)}=S_t^{(T)}=\{\begin{array}{ll}0\hfill & \text{if}t<T\hfill \\ 1\hfill & \text{if}t\ge T,\hfill \end{array}$$ (3)

$$I_t^{(T)}=P_t^{(T)}=\{\begin{array}{ll}0\hfill & \text{if}t\ne T\hfill \\ 1\hfill & \text{if}t=T,\hfill \end{array}$$ (4)

or

$$I_t^{(T)}=R_t^{(T)}=\{\begin{array}{ll}0\hfill & \text{if}t<T\hfill \\ t-T+1\hfill & \text{if}t\ge T.\hfill \end{array}$$ (5)

In practice, two of the most common models for the error are the autoregressive AR(1), and integrated moving average IMA(1), which correspond to p = 1, d = 0, q = 0 and p = 0, d = 1, q = 1. In the case of a step intervention, the SIA model implies that for t ≥ T + b, an increase of ω occurred. So the SIA model with a step intervention can be regarded as the time-series generalization of the standard two-sample test for a change in location. In practice, this is one of the most frequently applicable models. Pulse interventions are useful for dealing with outliers (Chang, Tiao, and Chen 1988). A ramp intervention has been used to model the recovery trend in stratospheric ozone (Reinsel et al. 2002).

The SIA model may be generalized by allowing for multiple interventions and other types of interventions, as well as for seasonal ARIMA errors and possible covariates (Tiao et al. 1990; Weatherhead et al. 1998; Reinsel 2002; Reinsel et al. 2002). All of these situations are easily handled with the methods discussed in Sections 2.2 and 2.3. Power computations, although possible, are less useful when applied to dynamic response interventions, for the reasons explained in Appendix B.

2.2 Information Matrix

Letting λ₁ = (ξ, ω) and λ₂ = (φ₁,…, φ_p, θ₁,…, θ_q, f), it is shown in Appendix A that the expected Fisher information matrix is block diagonal with blocks, ℐ_λ1 and ℐ_λ2 corresponding to λ₁ and λ₂. For the first block,

$${\mathcal{I}}_{\xi ,\omega }={\sigma }_{\mathbf{a}}^{-2}{\mathbf{J}}^{\prime }{\mathbf{\Gamma }}_n^{-1}\mathbf{J},$$ (6)

Where ${\sigma }_{\mathbf{a}}^{-2}{\mathbf{\Gamma }}_n^{-1}$ is the inverse of the covariance matrix of the stationary component and J is an n × 2 matrix with 1 in the first column and ${\nabla }^d{I}_t^{(T)}$, t = 1,…,n, in the second column. The Trench algorithm (Golub and Van Loan 1983) provides a computationally efficient method for computing ${\mathbf{\Gamma }}_n^{-1}$. An expression essentially equivalent to (6) was obtained by Tiao et al. (1990) and Weatherhead et al. (1998) using generalized least squares. Assuming approximate normality of the estimates, the asymptotic variance of the maximum likelihood estimate of ω is found by taking the (2, 2) element of the inverse of (6),

$${\sigma }_{\widehat{\omega }}=\sqrt{\left({\mathcal{I}}_{1,1}/({\mathcal{I}}_{1,1}{\mathcal{I}}_{2,2}-{\mathcal{I}}_{1,2}^2)\right)},$$ (7)

where ℐ_i,j denotes the (i, j) entry in the matrix ℐ_{ξ, ω}. If the constant term, ξ, is not present, then ${\sigma }_{\widehat{\omega }}=1/\sqrt{{\mathcal{I}}_{2,2}}$. When there is an extensive amount of data before the intervention, it is sometimes helpful to simply correct the series by its sample mean and assume that ξ = 0 (Tiao et al. 1990).

The results of Pierce (1972) provide a computationally efficient approximation to (6) when f = 0. From Pierce [1972, eq. (3.2)] we can write the Fisher information for (ξ, ω) based on n observations as

$${\mathcal{I}}_{\xi ,\omega }={\sigma }_{\mathbf{a}}^{-2}\left(\begin{array}{cc}n{\kappa }^2& \kappa {\sum }_t{v}_t\\ \kappa {\sum }_t{v}_t& {\sum }_t{v}_t^2\end{array}\right),$$ (8)

where κ = − φ (1)/θ (1) and v_t = −φ (B)/θ (B)w_t, where $w_t={\nabla }^d{I}_t^{(T)}$. Without loss of generality, we take b = 0, because if b > 0, the formulas hold with T replaced by T + b. Provided that T is not too small and T is not too close to n, (8) yields almost identical values to the more exact formula given in (6). New explicit expressions, using Pierce’s approximation for AR(1) and IMA(1) cases, are given in Tables 1 and 2 for step, pulse and ramp interventions.

Table 1.

Information Matrix for Simple Intervention Analysis With AR(1) Errors

Type	Information matrix entries
Step	${\mathcal{I}}_{1,2}/{\sigma }_{\mathbf{a}}^2=(n-T){(1-{\phi }_1)}^2+1-{\phi }_1$
	${\mathcal{I}}_{2,2}/{\sigma }_{\mathbf{a}}^2=(n-T){(1-{\phi }_1)}^2+1$
Pulse	${\mathcal{I}}_{1,2}/{\sigma }_{\mathbf{a}}^2=1-{\phi }_1^2$
	${\mathcal{I}}_{2,2}/{\sigma }_{\mathbf{a}}^2=1-{\phi }_1^2$
Ramp	${\mathcal{I}}_{1,2}/{\sigma }_{\mathbf{a}}^2=(1+n-T)(1-{\phi }_1)(2+n-T-(n-T){\phi }_1)/2$
	$\begin{array}{l}{\mathcal{I}}_{2,2}/{\sigma }_{\mathbf{a}}^2=(1+n-T)(6+7n+2n^2-7T-4nT+2T^2-8n{\phi }_1\\ -4n^2{\phi }_1+8T{\phi }_1+8nT{\phi }_1-4T^2{\phi }_1+n{{\phi }_1}^2+2n^2{\phi }_1^2-T{\phi }_1^2\\ -4nT{\phi }_1^2+2T^2{\phi }_1^2)/6\end{array}$

NOTE: This table gives the (1, 2) and (2, 2) entries, ${\mathcal{I}}_{1,2}/{\sigma }_{\mathbf{a}}^2$ and ${\mathcal{I}}_{2,2}/{\sigma }_{\mathbf{a}}^2$. For each intervention type, ${\mathcal{I}}_{1,1}/{\sigma }_{\mathbf{a}}^2=n{(1-{\phi }_1)}^2$, and the (2, 1) entry is obtained by symmetry.

Table 2.

Information Matrix for Simple Intervention Analysis With IMA(1) Errors

Type	Information matrix entries
Step	${\mathcal{I}}_{1,2}/{\sigma }_{\mathbf{a}}^2={(1-{\theta }_1)}^{-2}(1-{\theta }^{n+1-T})$
	${\mathcal{I}}_{2,2}/{\sigma }_{\mathbf{a}}^2={(1-{\theta }_1^2)}^{-1}(1-{\theta }^{2(n+1-T)})$
Pulse	${\mathcal{I}}_{1,2}/{\sigma }_{\mathbf{a}}^2={(1-{\theta }_1)}^{-1}{\theta }_1^{n-T}$
	${\mathcal{I}}_{2,2}/{\sigma }_{\mathbf{a}}^2={(1+{\theta }_1)}^{-1}2(1+{\theta }^{2(n-T)+1})$
Ramp	${\mathcal{I}}_{1,2}/{\sigma }_{\mathbf{a}}^2={(1-{\theta }_1)}^{-3}(n+1-T+{\theta }_1^{n+2-T}-(n+2-T)\theta )$
	$\begin{array}{l}{\mathcal{I}}_{2,2}/{\sigma }_{\mathbf{a}}^2={(1+\theta )}^{-1}{(1-{\theta }_1)}^{-3}(2{\theta }^{2+n+T}(1+\theta )-{\theta }^{4+2n}\\ +{\theta }^{2T}(n+1-T-2\theta -(2+n-T){\theta }^2))\end{array}$

NOTE: For θ₁ = 0, set ${\theta }_1^0=1$. The table gives the (1, 2) and (2, 2) entries, ${\mathcal{I}}_{1,2}/{\sigma }_{\mathbf{a}}^2$ and ${\mathcal{I}}_{2,2}/{\sigma }_{\mathbf{a}}^2$. For each intervention type, ${\mathcal{I}}_{1,1}/{\sigma }_{\mathbf{a}}^2=(n-1)/{(1-{\theta }_1)}^2$, and the (2, 1) entry is obtained by symmetry.

From (6), it follows that for consistency of the estimates ξ̂ and ω̂, ℐ_ξ,ω/n (or, equivalently, J′J/n) must converge to a nonsingular matrix. For the intervention analysis models defined by (2)–(5), this occurs provided that

$$\frac{1}{n}\sum _{t=1}^n{\nabla }^d{I}_t^{(T)}\to c,c>0,c\ne 1.$$ (9)

If the constant term, ξ, is assumed to be known or 0, then only c > 0 is needed. This result is certainly not the whole story from an application standpoint. In Section 2.5 we show, using simulation experiments, that the empirical variances may be accurately estimated from (7) even when (9) is not satisfied.

2.3 Power and Sample Size

The null hypothesis ℋ₀: ω = 0 can be tested using two asymptotically equivalent methods. The first method, referred to as the “Z-test,” uses Z = ω̂/σ̂_ω̂, where ω̂ is the maximum likelihood estimate for ω and σ̂_ω̂ is its estimated standard error. Note that σ_ω̂, the standard error of ω̂, depends only on the underlying ARIMA model in the preintervention period, and so it can be estimated before the postintervention data are obtained. A second, asymptotically equivalent method is to use a likelihood ratio test.

The asymptotic theoretical power function for the Z-test of the null hypothesis ℋ₀: ω = 0 against the two-sided alternative at level α is Pr{|ω̂| > Z_1−α/2σ_ω̂|ω}, where Z_1−α/2 is the upper (1 − α/2)-quantile in the standard normal distribution. For brevity, the asymptotic theoretical power function is referred to simply as the “power function.” In practice, this power function is approximated by replacing σ_ω̂ by an estimate, σ̂_ω̂, based either on the preintervention data or on other prior knowledge. Often it is more convenient to use the rescaled parameter, δ = ω/σ, where σ² is the variance of the stationary error component, because in this case knowledge of σ² is not needed. The power function may be expressed in terms of δ as

$$\mathrm{\Pi }(\delta )=\mathrm{\Phi }\left(-{\mathcal{Z}}_{1-\alpha /2}-\delta \sigma /{\sigma }_{\widehat{\omega }}\right)+1-\mathrm{\Phi }\left({\mathcal{Z}}_{1-\alpha /2}-\delta \sigma /{\sigma }_{\widehat{\omega }}\right),$$ (10)

where Φ(·) denotes the cumulative distribution function of the standard normal. If the variance of the preintervention series, σ², is known or estimated, then the power function for ω is Π(ω/σ). Equation (10) should be adjusted if only a one-sided alternative is under consideration.

As was done by Tiao et al. (1990), it is sometimes of interest to estimate the amount of additional data needed to detect an intervention of a specified magnitude with a prescribed power. The power function Π(δ) may be expressed more fully as a function of the test level α and the other underlying parameters n and T, so we can write the power function more fully as Π(δ, α, n, T). For a fixed α = α⁽⁰⁾, δ = δ⁽⁰⁾, and a prescribed power Π⁽⁰⁾, we may estimate the number of additional data values, m, that are required by numerically solving the equation Π(δ⁽⁰⁾, α⁽⁰⁾, T + m − 1, T) = Π⁽⁰⁾. If, as in the geophysical datasets considered by Tiao et al. (1990), there is extensive preintervention data, we may assume that the mean is known and take T = 1 and solve Π(δ⁽⁰⁾, α⁽⁰⁾, m, 1) = Π⁽⁰⁾. This technique is illustrated in Section 2.4, where it is also explained that in some situations, due to the limitations imposed by the model, there is no solution for m.

In general, the power and sample size computations for interventions with ARIMA and fractional ARIMA errors are easily done using an advanced quantitative programming environment, such as Mathematica, MatLab, S, or Stata. In the case of SIA with AR(1) or IMA(1) errors, power computations can even be done on a hand calculator.

2.4 Numerical Illustrations

In this section the power and sample size computations are illustrated for the SIA with a step intervention with AR(1), IMA(1), and fractionally differenced white noise. First, an approximation to the detection limit, δ′, is derived for the step intervention in an SIA model with unknown mean and stationary short-memory errors, with f = d = 0 and a fixed number, T − 1, of preintervention observations. The variance of the estimate, δ̂, may be written as var(δ̂) ≐ γ_δ/T, where ${\gamma }_{\delta }={\sum }_{k=-\infty }^{\infty }{\gamma }_k/{\gamma }_0$, γ_k is the autocovariance function for the stationary preintervention series, and γ₀ = σ². To achieve 90% power, Pr{(δ̂−δ′)/SE(δ̂)>1.96− δ′/SE(δ̂)} ≐ 9. Hence,2− δ&prime;/SE(δ̂) ≐ −1.3. So δ′ ≐ 3.3SE(δ̂).

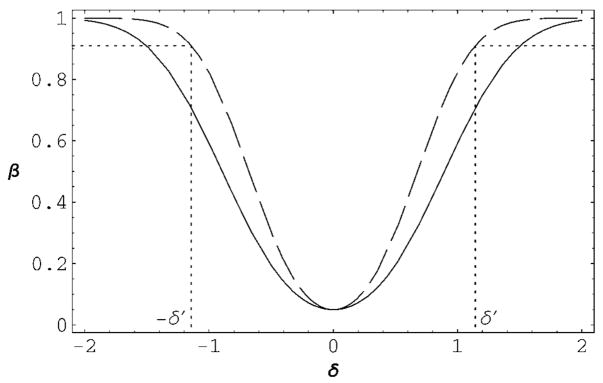
Using Table 1, the power curve for the AR(1) with unknown mean, n = 50, T = 25, and φ₁ = .5, σ_ω = .526681. With $\sigma =1/\sqrt{(1-{\phi }_1^2)}=1.1547$, the power curve is Π(δ) = 1 + Φ(−1.960 − 2.192 × δ) − Φ(1.960 − 2.192 × δ). This and the power curve obtained by letting n → ∞ are shown in Figure 1, as is as the approximate detection level, ${\delta }^{\prime }\doteq {\gamma }_{\delta }/\sqrt{T}=1.14$. For comparison, the exact value of δ′ found by numerically solving Π(δ′, .5, 10⁹, 25) = .9 is δ′ = 1.12. Assuming an unknown mean and that T = 25, we can find m, the number of additional observations needed to achieve a prescribed power level. For example, for 90% power with δ⁽⁰⁾ = 1.5, solving Π(1.5, .05, 25 + m − 1, 25) = .9, we find m = 23. In the known mean case, taking T = 1, we find m = 10. In the unknown mean case, if δ⁽⁰⁾ ≤ γ_δ, then there is no solution, but if the mean is known, then m can always be found.

Figure 1.

Comparison of Power Curves for n = 50, T = 25, and n = ∞, T = 25. The solid curve represents for n = 50, T = 25; the dashed curve, n = ∞, T = 25. The approximate detection limit, δ′ ≐ 1.143, is also shown.

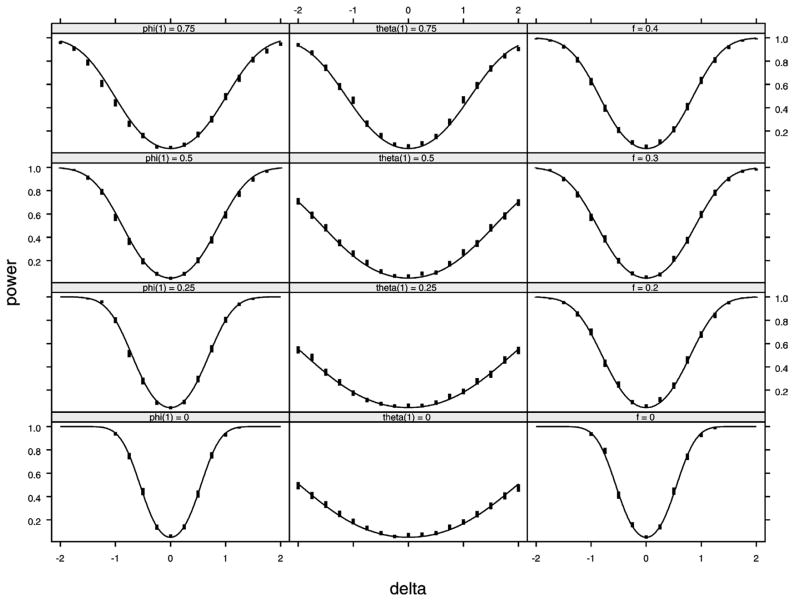
The middle panels of Figure 2 illustrate the power curves for an IMA(1) with n = 50 and T = 25. With θ₁ = .5, Π(δ) = 1 + Φ (−1.960 − 1.252 × δ) − Φ (1.960 − 1.252 × δ).

Figure 2.

Comparison of Empirical and Theoretical Asymptotic Power in the SIA Model With AR(1), IMA(1), and Fractionally Differenced White Noise. The parameter δ = ω/σ is the rescaled step size. The solid curve shows the theoretical power defined in (10). The vertical bars show the width of a 95% confidence interval for the empirical power in 1,000 simulations of the model. The AR(1) and IMA(1) parameters φ₁ and θ₁ are denoted by phi(1) and theta(1).

Because long-memory or fractional time series have also been suggested for various types of geophysical data, it is of interest to examine the impact of this type of process on our ability to detect interventions. Table 3 compares the power of a two-sided 5% level test of the fractionally differenced white noise model p = d = q = 0 with f = .2 and f = .4 to the corresponding approximating ARMA(1, 1) when n = 50 and T = 25. The approximating ARMA(1, 1) model was determined by equating the first two autocorrelations in the fractional model with the first two autocorrelations in the ARMA(1, 1) model and solving to obtain the parameters φ₁ and θ₁. In the first case with f = .2, the power is almost identical; in the second case with f = .4, the power is slightly higher for the ARMA(1, 1) approximation. This suggests that long-term memory in the fractional noise model has little effect on the power when the length of the series is moderate, as in this example with n = 50 and T = 25. For sufficiently long time series, the effect on long memory is much more important, and the ARMA(1, 1) approximation does not hold.

Table 3.

Power Function, Π (δ), for Fractionally Differenced White Noise With Parameter f and the Approximating ARMA(1, 1) Model for a Two-Sided 5% Level Test in the SIA Step Intervention Model With n = 50 and T = 25

δ	f = .2	f = .4
0	.050, .050	.050, .050
.5	.198, .202	.086, .076
1.	.602, .612	.198, .156
1.5	.914, .920	.384, .291
2.	.993, .994	.602, .468
2.5	1.000, 1.000	.792, .651
3.	1.000, 1.000	.914, .805

NOTE: The first entry in each pair is for the fractional model, and the second is for the ARMA(1, 1) model. The parameters in the approximating ARMA model are φ₁ = .667, φ₂ = .451 and φ₁ = .875, φ₂ = .405 corresponding to f = .2 and f = .4.

2.5 Simulation Experiment

The power function derived in (10) relies on the asymptotic normality of the maximum likelihood estimator, and so it is helpful to check its accuracy by simulation. We do this by comparing the power function with the empirical power function, Π̂. For each simulated time series, all parameters in the model were estimated by exact maximum likelihood estimation, and the Z-test was computed. The empirical power, Π̂, of a two-sided 5% test is then the proportion of times that the absolute value of this Z-statistic exceeded 1.96 in absolute value, and the 95% confidence interval for Π is $\widehat{\mathrm{\Pi }}\pm 1.96\sqrt{(\widehat{\mathrm{\Pi }}(1-\widehat{\mathrm{\Pi }})/N)}$, where N is the number of simulations. For each model and each parameter setting, N = 1,000.

The model in (2) was simulated with n = 50 and T = 25 and AR(1) errors with φ₁ = 0, .25, .5, .75, ω = δσ, where δ = 0, ±.25,…, ±2.0. The empirical power confidence limits and theoretical power given by (10) are compared in Figure 2. It is seen that (10) provides an accurate approximation. IMA(1) is a commonly occurring nonstationary time series model. Figure 2 also compares the theoretical and empirical powers for the case with n = 50 and T = 25 using a two-sided Z-test at the 5% level. Once again, it is seen that (10) holds very well despite the small sample size. The values selected for θ₁ are positive, because this is the most common situation in practice. The power improves, as expected, as θ₁ increases from 0 to 1. Notice that this model does not satisfy (9). The last column of Figure 2 compares the empirical and theoretical powers in the case of fractionally differenced white noise, p = q = d = 0 for f = .0, .2, .3, .4. The approximation to the theoretical power improves with increasing f . The simulations shown in Figure 2 were repeated using the likelihood-ratio test, and essentially equivalent results were obtained.

In conclusion, the simulations in Figure 2 suggest that for practical purposes, if n, T, and n − T are not too small, then the asymptotic theoretical power curve provides a good small-sample approximation. Alternatively, the simulations show that ω̂ is well approximated using its large-sample approximation even for moderately small samples. As already noted, σ_ω̂ also must be estimated by σ̂_ω̂ using either the preintervention data or an estimate of its likely autocorrelation function. In practice, as in the example in Section 3.1, a range of likely parameter values is often used to indicate a range of possible power curves.

2.6 Model Uncertainty

Box, Jenkins, and Reinsel (1994) found that both the ARMA(1, 1) and IMA(1) fit series A, chemical process concentrations, about equally well. Both models give similar onestep-ahead forecasts, but very different long-run forecasts. The situation is similar with the power functions for these two models.

Consider a hypothetical step intervention that occurs immediately after the last observation. In this case T = 198, and the power curve as a function of ω is tabulated for a few selected values in Table 4 for a two-sided 5% test assuming that m postintervention observations are available for m = 5 and m = 50. When m = 5, the power curves are quite similar, but for m = 50, the power increases for the ARMA model but stays essentially the same for the IMA model. For example, Table 4 shows that there is a 75% chance of detecting a change of .6 with just five postintervention observations.

Table 4.

Power Comparison for Step Interventions With ARMA(1, 1) and IMA(1) Errors for Series A With n = 197 + m and T = 198

	ARMA(1, 1)		IMA(1)
ω	m = 5	m = 50	m = 5	m = 50
.2	.141	.205	.141	.143
.3	.258	.398	.258	.264
.4	.415	.621	.416	.425
.5	.588	.809	.589	.600
.6	.745	.925	.746	.756
.7	.863	.978	.864	.872

NOTE: The models’ other parameters are {φ₁ = .9087, θ₁ = .5758, σ_a = 0.3125} and {θ₁ = .7031, σ_a = .3172}.

2.7 Forecast-Actuality Significance Test

Box and Tiao (1976b) described an omnibus significance test for detecting whether an intervention has occurred. If a_t, t = T,…, n, denote the one-step-ahead prediction errors of an assumed model, then the test statistic may be written as $Q={\sum }_{t=T}^n{a}_t^2/{\sigma }_{\mathbf{a}}^2$. If the intervention has no effect, then Q is approximately chi-squared distributed on m = n − T + 1 degrees of freedom. This significance test is easy to apply and does not require specification of an intervention model and its estimation. However, as might be expected, the loss of power can be considerable, as we now demonstrate.

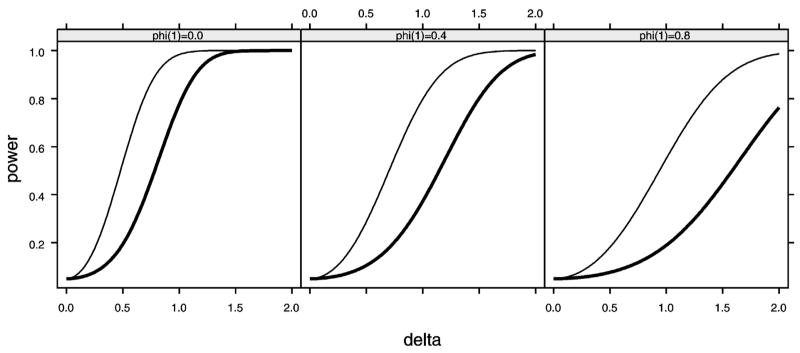
As an example, consider the SIA model with a step intervention. Then it can be shown, using (4) of Box and Tiao (1976b), that $Q=\parallel \omega {\mathbf{1}}_m^{\prime }\mathit{\pi }/{\sigma }_{\mathbf{a}}+\mathbf{a}/{\sigma }_{\mathbf{a}}\mid {\mid }^2$, where 1_m denotes the m-dimensional vector with a 1 in each position, a = (a_T,…, a_n), and π = (π_i−j) is the lower triangular matrix with (i, j) entry π_i−j, where π_k is the coefficient of B^k in the expansion ∇^d φ(B)/θ(B) = 1 + π₁B + π₂B² + ···. So Q has a chi-squared distribution with m degrees of freedom and non-centrality parameter $\nu =({\omega }^2/{\sigma }_{\mathbf{a}}^2)\parallel {\mathbf{1}}_m^{\prime }\mathit{\pi }\mid {\mid }^2$, and hence the large-sample power function can be computed. Figure 3 compares the power of this significance test with that of the SIA model hypothesis test for an example with n = 120, T = 101, and AR(1) errors. Figure 3 shows that the power of the significance test can be substantially less than that of the intervention analysis hypothesis test.

Figure 3.

Comparison of Power Functions for a SIA Model With a Step Intervention With AR(1) Errors and the Forecast-Actuality Significance Test for a Two-Sided Test at the 5% Level. The model parameters are n = 120, T = 101, delta = δ = ω/σ, and phi(1) = φ₁. The solid thin curve shows the SIA model-based hypothesis test, and the solid thick curve shows the omnibus significance test using Q. Because both power functions are symmetric about δ = 0, only the upper half is shown.

3. ILLUSTRATIVE APPLICATIONS

3.1 Traffic Safety and Public Policy

On May 1, 1996, liquor bar closing time in Ontario was changed from 1 AM to 2 AM. In a proposed intervention analysis, we wished to examine the possible effect of this change on late-night automobile fatalities. The data for this study comprised the total number of fatalities each month in Ontario during the hours of 11 PM to 4 AM for a period of years before and after May 1, 1996. For comparison, we also collected similar time series data for Michigan and New York. Data for this analysis were expensive to obtain, because raw records needed to be assembled, cleaned, and aggregated from sources in various jurisdictions. Initially, we planned to obtain monthly time series on the total number of fatalities from January 1994 to December 1998. This would yield n = 60 observations, and with the intervention occurring at T = 36. At additional cost, we could obtain complete monthly time series covering the period January 1992–December 1998, which corresponds to n = 84 and T = 48. We were interested to know whether (n = 60, T = 36) or (n = 84, T = 48) would be sufficient to detect change of σ or greater with a reasonably high probability, where σ is the standard deviation of the preintervention series.

Based on previous experience with similar time series (Vingilis, Blefgen, Lei, Sykora, and Mann 1988), we expected the time series to exhibit small autocorrelations that may be modeled by an AR(1) model with parameter φ₁ ≤ .5. The intervention was expected to cause an increase in late-night fatalities, so a one-sided upper-tail test is appropriate. The power function in this case is Π(δ) = 1 − Φ(1.645 − 2.362 × δ). Table 5 gives the power of a 5% upper-tail test for these two plans for various φ₁. When φ₁ = .5, Table 5 shows that (n = 84, T = 48) has a 86.7% chance of detecting a step intervention whose magnitude is only one standard deviation of the error component, whereas the corresponding power for (n = 60, T = 36) is 76.3%. The results of Table 5 demonstrated to the satisfaction of us and the granting agency that (n = 84, T = 48) had a good chance of detecting a meaningful change and was worth the extra expenditure.

Table 5.

Power Comparison for AR(1) Errors for (n = 60, T = 36) and (n = 84, T = 48)

δ	φ1 = 0	φ1 = .25	φ1 = .5	φ1 = .75
.000	.050, .050	.050, .050	.050, .050	.050, .050
.250	.245, .306	.186, .226	.146, .170	.124, .135
.500	.604, .736	.444, .555	.321, .395	.253, .288
.750	.889, .961	.729, .848	.550, .664	.431, .493
1.000	.985, .998	.914, .973	.763, .867	.624, .700
1.250	.999, 1.000	.983, .998	.904, .964	.790, .857
1.500	1.000, 1.000	.998, 1.000	.971, .994	.903, .946
1.750	1.000, 1.000	1.000, 1.000	.994, .999	.963, .984
2.000	1.000, 1.000	1.000, 1.000	.999, 1.000	.989, .996

NOTE: The first entry in each column corresponds to (n = 60, T = 36) and the second (n = 84, T = 48).

3.2 Detecting Ozone Turnaround

Tiao et al. (1990) used the SIA model with a ramp intervention with AR(1) errors to model the trend in monthly deseasonalized stratospheric ozone and other environmental variables. For simplicity, Tiao et al. (1990) assumed that the mean of the preintervention series was known. It may be shown that the expression obtained by Tiao et al. (1990, app. A) for σ_ω̂ is exactly equal to ${\sigma }_{\widehat{\omega }}=1/\sqrt{{\mathcal{I}}_{2,2}}$ using Table 1 with n = T and T = 1. Table 6 compares this result with the corresponding result obtained using the exact expected Fisher information matrix given in (6) for the same parameters as used by Tiao et al. (1990, table 1). When φ = .8, the difference is as high as 17%, but it decreases as the sample size increases. The approximation is very good for parameter values ≤.6. For most of the geophysical time series considered by Tiao et al. (1990), the degree of autocorrelation is quite low, so this approximation works well.

Table 6.

Comparison of Exact and Approximate Methods

Number of years	φ = .6	φ = .8
6	−6	−17
7	−5	−15
8	−5	−13
9	−4	−11
10	−4	−10

NOTE: The function g(T, φ) defined by Tiao et al. (1990) was computed using the exact form of the information matrix (6) and the approximation (8) for selected parameter values given in table 1 of Tiao et al. (1990). The entries in the table show the percentage difference, 100 × (EXACT − APPROXIMATE)/EXACT.

Tiao et al. (1990, table 2) also considered the number of years of monthly data needed to detect a ramp intervention for several geophysical time series of interest. In their computations it was assumed that T = 1 and that the mean was known. Table 7 computes the number of years of data needed for these time series under the assumptions that the mean is unknown but there are 30 years of prior data. The other assumptions about the data and the form of the intervention are the same as those of Tiao et al. (1990). The parameter δ shown in the table was based on the information supplied by Tiao et al. (1990). Specifically, δ = ω/(12 × σ̂), where φ̂₁ and σ̂ are as obtained by Tiao et al. (1990, table 2) and ω is as obtained by Tiao et al. (1990, pp. 20, 510). Note that ω was divided by 12, because the form of the intervention used by Tiao et al. (1990) was $R_t^{(T+1)}/12$. In conclusion, the estimate of the sample size required shown in Table 7 is in reasonable agreement with the results of Tiao et al. (1990).

Table 7.

Number of Years, n^*, for 90% Probability of Detecting a Prescribed Trend, δ Using a Two-Sided 5% Test Given 30 Years of Prior Data and Assuming AR(1) Errors With Estimated Parameter φ̂₁

	Tateno	Hohen	Wakkan	Bulawayo	Abidajan
φ̂1	.32	.05	.14	.43	.65
ω	.003	.003	.2	.2	.2
δ	.00758	.00543	.01042	.01282	.01111
N*	11.6	12.1	8.0	8.6	12.0
n*Tiao	14	14	10	10	13

NOTE: The last line of the table shows the comparable values given by Tiao et al. (1990, table 2).

4. CONCLUDING REMARKS

We have shown how the power function for an intervention analysis may be computed provided that we have an estimate of the ARIMA parameters in the preintervention time series or in some closely related time series. In the case of the SIA model with AR(1) or IMA(1) errors, the power function can be easily computed using a hand calculator. Such programs are freely available for the Texas Instruments TI-83 at the first author’s webpage. Mathematica and S software for computing the power functions and all tables and figures described in this article are also available there, as are various other supplements to this article.

The emphasis of this article has been on using the power function as an aid in selecting the sample size. In the case of the SIA model, if Π(ω′) = 1 − β′ for a 5% two-sided test of ℋ₀: ω = 0, then the usual 95% confidence interval for ω will contain 0 with probability β′ when ω = ω′. Thus the power function may be used as an aid in choosing the sample size so that a useful confidence interval is obtained. Instead of the power function, we could have focused on the width of a suitable interval estimate of ω. Because this also depends on an estimate of σ_ω̂, the methods presented are applicable. It may be noted that overemphasis on hypothesis tests has long been condemned, as was noted many years ago by Cox (1977). Nevertheless, as indicated by Cox (1977), such tests remain important in practice.

The power function depends strongly on the degree of autocorrelation in the preintervention time series. In the stratospheric ozone example, Section 3.2, a long preintervention series was available that enabled the model to be accurately estimated. In other cases, such as the traffic safety example in Section 3.1, the preintervention series is either unavailable or quite short. In such cases prior information may be available that indicates a range of likely models. As discussed in Section 3.1, this still may be very useful for planning purposes. A final note of caution, power computations should be used only before the data analysis is done (Hoenig and Heisey 2001; Lenth 2001) and should never be used to compute the observed power after a test of hypothesis has already been carried out.

APPENDIX A: DERIVATION OF THE INFORMATION MATRIX

The log-likelihood function, apart from a constant, may be written as

$$L({\mathit{\lambda }}_1,{\mathit{\lambda }}_2,{\sigma }_{\mathbf{a}}^2)=-log(\sigma )-log(det({\mathbf{\Gamma }}_n))-\frac{1}{2{\sigma }_{\mathbf{a}}^2}{\mathbf{y}}^{\prime }{\mathbf{\Gamma }}_n^{-1}\mathbf{y},$$ (A.1)

where y is the column vector of length n − d with tth entry ${\nabla }^d{z}_t-\xi -\omega {\nabla }^d{S}_t^{(T)}$, t = d + 1,…, n. Then ∂y/∂ξ = (−1, …, −1). Similarly, $\partial \mathbf{y}/\partial \omega =(-S_1^{(T)},\dots ,-S_n^{(T)})$. Hence

$$\begin{array}{l}{\mathcal{I}}_{{\mathit{\lambda }}_1}=-E\left({\partial }_{{\mathit{\lambda }}_1,{\mathit{\lambda }}_1}^{2}L({\mathit{\lambda }}_1,{\mathit{\lambda }}_2,{\sigma }_{\mathbf{a}}^2)\right)\\ =\frac{1}{{\sigma }_{\mathbf{a}}^2}{\mathbf{J}}^{\prime }{\mathbf{\Gamma }}_n^{-1}\mathbf{J},\end{array}$$ (A.2)

where J is as in (6). Because $E({\partial }^{2}L({\mathit{\lambda }}_1,{\mathit{\lambda }}_2,{\sigma }_{\mathbf{a}}^2)/(\partial {\mathit{\lambda }}_1\partial {\mathit{\lambda }}_2))=\mathbf{0}$ and $E({\partial }^{2}L({\mathit{\lambda }}_1,{\mathit{\lambda }}_2,{\sigma }_{\mathbf{a}}^2)/(\partial {\mathit{\lambda }}_1\partial {\mathit{\lambda }}_2))=\mathbf{0}$, the information matrix is block diagonal.

APPENDIX B: INTERVENTIONS WITH A DYNAMIC RESPONSE

For completeness, we also discuss the intervention analysis model with a dynamic response to the intervention, which may be written as

$${\nabla }^d{z}_t=\xi +\omega (B)/\delta (B){\nabla }^d{B}^b{I}_t^{(T)}+{\nabla }^{-f}\frac{\theta (B)}{\phi (B)}{a}_t,t=1,\dots ,n,$$ (B.1)

where ω(B) = ω₀ + ω₁B + ··· ω_rB^r and δ(B) = δ₀ − δ₁B − ··· δ_sB^s. For stability of the transfer function, it is assumed that all roots of δ(B) = 0 lie outside the unit circle. As in Appendix A, the exact information matrix for the parameters is ${\mathit{\lambda }}_1=(\xi ,{\omega }_0,\dots ,{\omega }_r,{\delta }_1,\dots ,{\delta }_s){\mathcal{I}}_{{\mathit{\lambda }}_1}={\sigma }_{\mathbf{a}}^{-2}{\mathbf{J}}^{\prime }{\mathbf{\Gamma }}_n^{-1}\mathbf{J}$, where J is an n − d × (2 + r + s) matrix with rows (1, u_t,…, u_t−r, v_t,…, v_t−s) for t = 1,…, n − d, where $u_{t-j}={\nabla }^d(1/\delta (B))I_{t-j}^{(T)}$ and $v_{t-j}={\nabla }^d(\omega (B)/\delta (B))I_{t-j}^{(T)}$. Alternatively, the large-sample approximation given by Pierce (1972) may be used. The steady-state gain (Box et al. 1994, sec. 10.1.1), which measures the long-run change of the intervention, is defined by g = (ω₀ + ··· + ω_r)/(1−δ₁ − ··· − δ_s). The maximum likelihood estimates for the model may be used to form the estimate of g, ĝ . Using a Taylor series linearization, the standard deviation of ĝ is given by ${\sigma }_{\widehat{g}}=\sqrt{({\mathbf{d}}_{\zeta }^{\prime }{\mathbf{V}}_{\zeta }{\mathbf{d}}_{\zeta })}$, where V_ζ is obtained by dropping the first row and column from ${\mathcal{I}}_{{\mathit{\lambda }}_1}^{-1}$ and d_ζ = (∂g/∂ω₀, …, ∂g/∂ω_r,∂g/∂δ₁,…, ∂g/∂δ_S). For dynamic intervention analysis models, we may consider testing ℋ₀: g = 0 using the Z test. Notice that when s > 0, we need estimates of all parameters in the full intervention model to estimate σ_ĝ. This limits the applicability of this approach, because even if the preintervention series were known, it is not likely that such precise information would be available for the intervention parameters. Often the SIA model can be used to get an approximation to the power in this case.

As a numerical illustration, consider the dynamic step intervention model, $z_t=\xi +{\omega }_0(1)/(1-{\delta }_{1}B)S_t^{(T)}+a_t/(1-{\phi }_{1}B)$, t = 1,…, n. Taking n = 50, T = 25, ξ = 0, φ₁ = .5, and ${\sigma }_{\mathbf{a}}^2=1$, Table B.1 compares the power of a 5% two-sided test, ℋ₀: g = 0, where g = ω₀(1), with that of the Z-test ${\mathscr{H}}_0:{\omega }_0^{(2)}=0$ in the corresponding SIA model defined by $z_t=\xi +{\omega }_0^{(2)}{S}_t^{(T)}+a_t/(1-{\phi }_{1}B)$, where ${\omega }_0^{(2)}=g$ and the other parameter settings are the same. On an intuitive basis, the effect in the SIA model is slightly larger, so one might expect the power in the SIA model to be slightly larger. Table B.1 shows, comparing the first two entries in each triplet, that this is exactly what happens. The third entry in each triplet in Table B.1 is the empirical power of a two-sided 5% test of ${\mathscr{H}}_0:{\omega }_0^{(2)}=0$ when the SIA model is fitted to a time series generated by the dynamic step intervention model. A total of 1,000 simulations were used for each model. The empirical power is predicted well by the theoretical asymptotic power for the SIA model. These simulations were repeated with various values of the parameter φ, and similar results where found when −1 < φ ≤ .5. For φ₁ > .5, there was a much larger difference between the asymptotic theoretical power of the dynamic model and the step model. For example, with φ₁ = .9, ω₁ = .75 and δ₁ = .75, the asymptotic power for the two-sided 5% level gains test was only .199, whereas the predicted power using a SIA step intervention was .972. The empirical power of the two-sided 5% level test of ℋ₀: ω₁ = 0 in the step SIA model was .283. The general conclusion reached was that the step SIA model provides a useful approximation to the more complicated dynamic step intervention model provided that the autocorrelation is not too large. Further simulation results are available in the online supplements.

Table B.1.

Power Comparisons of the Dynamic Step Intervention Model With Simple Step Intervention When n = 50 and T = 25

δ0	ω0 = .5	ω0 =.75	ω0 = 1.0
.25	.226, .252, .241	.416, .490, .466	.879, .972, .880
.50	.439, .490, .445	.745, .827, .758	.997, 1.000, .974
.75	.673, .732, .692	.937, .972, .932	1.000, 1.000, .955

NOTE: The first entry in each triplet shows the theoretical power of a 5% two-sided test of ℋ₀: g = _0, where $g={\omega }_0^{(1)}/(1-{\delta }_1)$ in the dynamic step intervention model $z_t=\xi +{\omega }_0^{(1)}/(1-{\delta }_{1}B)S_t^{(T)}+a_t/(1-{\phi }_{1}B)$ with ξ = 0, φ₁ = .5, and ${\sigma }_{\mathbf{a}}^2=1$. The second entry is the theoretical power of a 5% test of ${\mathscr{H}}_0:{\omega }_0^{(2)}=0$ in the SIA model, $z_t=\xi +{\omega }_0^{(2)}{S}_t^{(T)}+a_t/(1-{\phi }_{1}B)$, where ${\omega }_0^{(2)}={\omega }_0^{(1)}/(1-{\delta }_1)$ and all other parameters are the same as in the dynamic model. The third entry is the empirical power, based on 1,000 simulations, for a two-sided 5% test of ${\mathscr{H}}_0:{\omega }_0^{(2)}=0$ when the SIA model is fitted to a time series generated by the dynamic step intervention model.