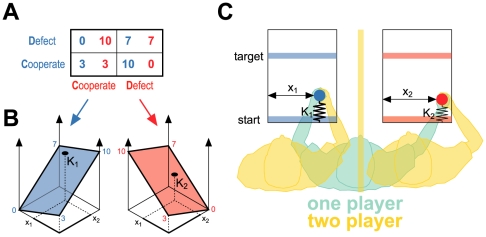
Figure 1. The prisoner's dilemma motor game.

(A) Pay-off matrix for the classical prisoner's dilemma for two players (players denoted by red and blue). Depending on the choice of each player there are four different outcomes in terms of years that each player will serve in prison. (B) The motor version of the prisoner's dilemma. Each player controls a cursor and moves from a starting bar to a target bar and experiences a force that resists forward motion. The force arises from a virtual spring that attaches the handle to the starting bar (the springs are only shown on the schematic and are not visible to the players). The stiffness of the springs (K₁ & K₂) can vary online and each depends on the x-positions of both players' cursors (x₁ & x₂). (C) Continuous cost landscape for the motor prisoner's dilemma game. Each pair of x-positions (x₁, x₂) corresponds to a spring constant for each player. The corners of the plane correspond to the classical prisoner's dilemma matrix (A) and intermediate spring constants are obtained by linear interpolation. The current spring constants experienced by the players in B are shown by the points on the surface. The game was played by eight pairs of players and by eight individual players bimanually.