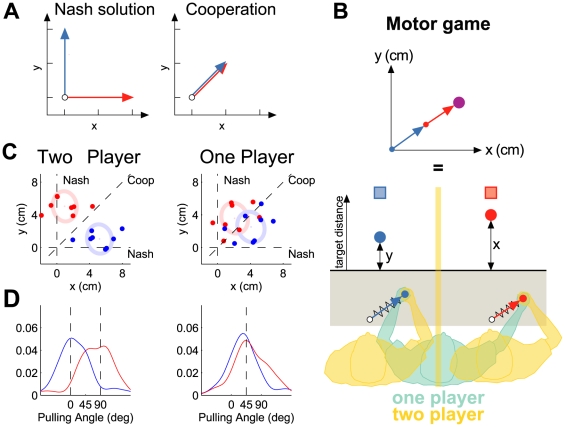
Figure 5. The rope-pulling game.

(A) The rope-pulling game in which a mass (circle) is pulled by two players. The arrows show the direction of force for two players for the Nash and cooperative solutions. Red and blue colors represent right and left handles throughout. (B) The motor version of the rope-pulling game. The position of a virtual mass is the sum of the displacements of the two handle positions from their origin (blue and red displacement vectors). However, the visual feedback is only a one-dimensional cursor location that is the y and x values of the mass position for players 1 and 2 respectively. Each player is required to reach a visual target with their cursor. Each robot was used to simulate the forces that would arise from a spring (with constant stiffness) attached between the handle and its origin. The arrow vectors and springs are only shown on the schematic and are not visible to the participants (grayed area not visible). For the one player game, a single participant controls both handles. The game was played by 4 pairs of participants and by 4 different participants individually. (C) Mean end points for each pair of left and right players for the last 40 trials in each set. The ellipses are centered at the average end points across all participants and indicate one standard error. (D) Smoothed frequency histograms (Gaussian kernel sd 20°) of pulling angles for the two-player condition (left: Nash equilibrium shown by vertical lines) and for the one player condition (right: cooperative solution shown by vertical line).