Forward locomotion of the nematode C. elegans is achieved through modulation of a single gait

Abstract

The ability of an animal to locomote through its environment depends crucially on the interplay between its active endogenous control and the physics of its interactions with the environment. The nematode worm Caenorhabditis elegans serves as an ideal model system for studying the respective roles of neural control and biomechanics, as well as the interaction between them. With only 302 neurons in a hard-wired neural circuit, the worm’s apparent anatomical simplicity belies its behavioural complexity. Indeed, C. elegans exhibits a rich repertoire of complex behaviors, the majority of which are mediated by its adaptive undulatory locomotion. The conventional wisdom is that two kinematically distinct C. elegans locomotion behaviors—swimming in liquids and crawling on dense gel-like media—correspond to distinct locomotory gaits. Here we analyze the worm’s motion through a series of different media and reveal a smooth transition from swimming to crawling, marked by a linear relationship between key locomotion metrics. These results point to a single locomotory gait, governed by the same underlying control mechanism. We further show that environmental forces play only a small role in determining the shape of the worm, placing conditions on the minimal pattern of internal forces driving locomotion.

Among the simplest animal nervous systems is that of the nematode worm Caenorhabditis elegans, “the hydrogen atom” of systems neuroscience. The adult hermaphrodite is 1 mm long and consists of a mere 959 nongonadal cells, of which exactly 302 are neurons. Furthermore, the availability of a detailed reconstruction of its invariant nervous system (White et al., 1986; Chen et al., 2006), including location, morphology, and interconnectivity of all the neurons, provides insight unparalleled in the animal kingdom. Nonetheless, translating this static circuit into an understanding of the rich behavioral dynamics of the worm remains an open and exciting question (Harel, 2003; de Bono and Maricq, 2005; Schafer, 2005).

Of particular significance is the locomotion subsystem, which is involved in most if not all of the worm’s behavior (from navigation and foraging to mating and aggregation). Until recently, however, C. elegans locomotion has not been extensively studied per se, instead being used primarily as a behavioral assay in genetic analysis, where crawling (e.g., Wittenburg and Baumeister, 1999; Sawin et al., 2000; Esmaeili et al., 2002; Chase et al., 2004, Davies et al., 2004; Mehta et al., 2004; Mohri et al., 2005; Darby et al., 2007) and, less often, swimming related statistics (e.g., Petersen et al., 2004; Chronis et al., 2007; McDonald et al., 2007; Tsechpenakis et al., 2008) are used to score phenotypes linked to a wide range of developmental, sensori-motor, neuromodulatory, and structural defects, to list but a few (see reviews in Jorgensen and Mango, 2002; Syntichaki and Tavernarakis, 2004; de Bono and Maricq, 2005). Worms are routinely maintained and observed in laboratories on agar surfaces where locomotion is limited to crawling.

The motor behavior of the worm is particularly interesting given the animal’s fully mapped nervous system. However, the worm’s locomotion dynamics derive, not only from the neuromuscular control system, but from a combination of internal control and the physical properties of the body, the environment in which it moves, and the interaction between these internal and external contributions. Thus the detailed and integrated modeling of the worm’s locomotion stands as a prime challenge to a broad, interdisciplinary scientific community.

We note that when studying the physical forces involved in the locomotion, it is important to consider the small size of the worm. At the scale of the worm, gravity and other inertial forces (proportional to the worm’s mass) are practically negligible. Instead, local properties of the environment dominate. This effect is captured by the Reynolds number, defined as the ratio of inertial forces to viscous forces of a medium. In a low Reynolds number environment such as the worm’s, locomotion can be likened to moving through treacle. The neuromuscular control and the properties of the body must therefore take such forces into account to achieve effective and robust locomotion.

C. elegans crawling and swimming

Currently, our understanding of C. elegans locomotion is largely restricted to the crawling behavior (slow, sinusoidal undulations) in which worms form grooves with their heads when moving through dense suspensions or on the surface of agar gels (Gray and Lissmann, 1964). In the latter case, although the mass of the worm is negligible, a thin film of water gives rise to strong capillary forces which press it against the surface, allowing it to carve a groove (Wallace 1958, 1969). The body can then push against the side-walls of this groove, increasing thrust. The effect of the groove can be represented by the ratio of forces resisting motion in the normal (perpendicular) and longitudinal directions to the local body surface, denoted K. In a viscoelastic environment K reduces to the ratio of the normal and longitudinal drag coefficients (Gray and Hancock, 1955).

Models of C. elegans locomotion have also generally been restricted to the crawling behavior and have primarily focused on the undulation pattern associated with forward motion and its sensori-motor control (Niebur and Erdös, 1991, 1993; Suzuki et al., 2005; Boyle and Cohen, 2008; Bryden and Cohen, 2008; Karbowski et al., 2008). The canonical model of C. elegans crawling due to Niebur and Erdös (1991) (NE) assumes a very stiff groove withK=10,000. Such strong lateral forces would allow the groove to maintain the sinusoidal waveform of the worm as well as to generate forward thrust, all with a minimal muscle activation pattern in which relatively few muscles are active at any one time. Interestingly, the NE model predicts that in the absence of a strong groove, the worm will straighten out, preventing further locomotion. In fact, when C. elegans is placed in water (M9 buffer), the crawling behavior is replaced by swimming (fast thrashing motion). Thus, despite intermediate behaviors being reported for another nematode species (Wallace, 1958), C. elegans is typically described as either swimming or crawling—two distinct gaits, each associated with a well defined waveform (Karbowski et al., 2006; Korta et al., 2007; Karbowski et al., 2008; Pierce-Shimomura et al., 2008).

To address this two-gait hypothesis we characterize the transition from swimming to crawling. If swimming and crawling really do represent distinct gaits, this would be marked by a discontinuous change in one or more locomotion metrics at some point during the transition between these behaviors (Alexander, 1989). Conversely, a smooth and continuous transition would suggest that swimming and crawling are achieved through modulation of a single gait.

RESULTS

Swimming and crawling correspond to a single gait

To characterize the transition between swimming and crawling we introduce a tunable environment in which the viscoelastic properties of the medium, and hence the stiffness of the groove, can be modulated from waterlike Newtonian conditions (with K of order 1) to strongly non-Newtonian media. We record the locomotion of freely moving worms fully immersed in gelatin solutions (see Methods), where increasing concentrations correspond to more viscoelastic media with a higher ratio of effective drag coefficients K. We also recorded motion on agar (the standard culture medium) for comparative purposes. Using specially developed software (Methods), we extract worm midlines and calculate locomotion metrics including the wavelength λ, amplitude A, and frequency f of undulations. We use a physiologically grounded version of wavelength, defined as the arc length of a single period along the body, that reflects the underlying pattern of muscle activation and more naturally links to neuromuscular locomotion models. We also conducted a rheological characterization of the various gelatin solutions (Methods). Unfortunately K is not readily measurable by these means and is particularly hard to estimate experimentally for small flexible objects moving in heterogeneous media, where bulk measurements are not appropriate. Instead, we use a physics simulator (described in Methods) to fit K to the motion of the worm, given its observed waveform in time.

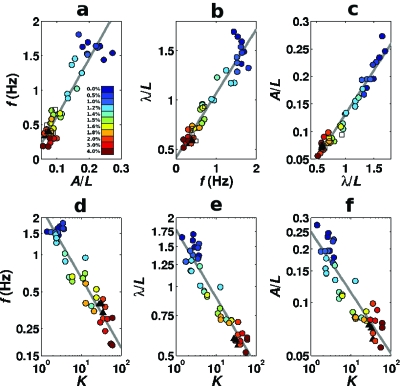
The results of this investigation are summarized in Fig. 1, which includes locomotion data recorded in 11 different gelatin concentrations as well as on the surface of agar (see Supplementary Movies for examples). Note that while locomotion on agar is comparable to that in 2% gelatin, our assay goes up to 4%. Thus the behaviors demonstrated here extend from swimming, through intermediate behaviors, to crawling and beyond. In marked contrast to what one would expect from the two-gait hypothesis, we find that across this entire range of environments there is a clear linear relationship between the frequency, amplitude, and wavelength of undulations [Figs. 1a, 1b, 1c], with no discontinuity in this transition. Moreover, when each of these locomotion metrics is plotted against our estimates of K [Figs. 1d, 1e, 1f], we find that all three of them decay smoothly and continuously. Thus, we find no evidence for the existence of distinct swimming and crawling gaits, nor for a switch between different modes of locomotion. Rather, our results strongly suggest that all C. elegans locomotory waveforms are achieved by a continuous modulation of a single gait.

Figure 1. (a)–(c) Proportionality of key locomotion parameters in a variety of environments (a range of gelatin concentrations, deformable agar surface, non-deformable membrane surface, with n ⩾3 replicates per environment).

Lines show the best linear fits to the data. (d)–(f) frequency, wavelength, and amplitude of the locomotion wave all decay smoothly with K in the different media (gelatin and agar, with n⩾3 replicates per environment). Lines show the best power-law fits to the data. Note the doubly logarithmic scales. In all graphs, filled circles show gelatin data. Different colors represent different gelatin concentrations. Agar and membrane data are represented by black triangles and white squares respectively.

The groove is not required for crawling

Our results are particularly surprising in light of the importance generally attributed to the groove in shaping the crawling waveform (Gray and Lissmann, 1964; Niebur and Erdös, 1991; Alexander, 2002) and the specific predictions of the NE model. Not only is the worm capable of modulating its locomotion properties smoothly, but the very low values of K we obtain for motion on agar (K=32±4), in the closest matching gelatin concentration of 2% (K=37±3) and even for 4% gelatin (K=58±3), suggest that these environments could lie outside the regime described by the NE model (with K=10⁴). We therefore implemented the NE model in computer simulations (Boyle et al., 2008) and found that as K is reduced from 10,000, undulations remain robust down to about K=1000 but gradually lose stability for lower values. For K⩽200, we find that undulations are no longer sustained even for a single undulation period. It therefore appears that locomotion on agar (and even in the stiffest gelatin tested) cannot rely on the strength of the groove to maintain the sinusoidal body shape. Rather, in this regime, the strong normal drag forces due to the groove serve only to generate thrust.

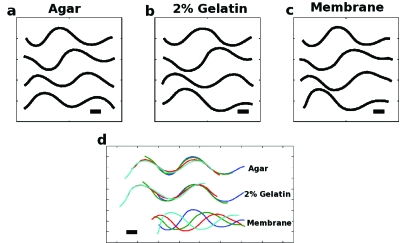
To further check this hypothesis, we sought to eliminate the presence of a groove altogether, by placing worms on a flat, non-deformable surface (Methods). The resulting locomotion was recorded and compared to that of worms on agar and in 2% gelatin [Figs. 2a, 2b, 2c]. The body waves produced in all three environments are very similar [λ_agar=(0.58±0.02)L, λ_2%gel.=(0.63±0.07)L and λ_surface=(0.65±0.06)L], where L is the body length of the worm. To verify the absence of a groove, we note that the worm produces minimal forward motion [Fig. 2d], implying that K is close to unity. For K=1 (an ideal surface with no forces except surface friction), theory predicts that the worm’s center of mass will remain stationary relative to the surface (Gray and Hancock, 1995).

Figure 2. Sequences of four midlines extracted from movies of worms moving in/on different media.

(a)–(c) Worm midlines have been displaced vertically, rotated, and aligned for clarity, with the head to the left and time increasing from top to bottom in quarter-period steps. The scale bar corresponds to approximately 0.1 mm. Estimated K values are (a) 35, (b) 35, and (c) 1.9. (d) Same midlines as above (a)–(c), still rotated, with the head to the left, but without removing the center of mass motion.

The above results strongly indicate that external forces play a much smaller role in shaping the locomotion than previously suspected. This in turn imposes a condition for the minimal muscle activation pattern that is sufficient to determine the body shape during normal locomotion, e.g., as found in alternative models of C. elegans crawling that neglect environmental forces (Bryden and Cohen, 2004, 2008; Karbowski et al., 2008).

C. elegans does not exhibit power saturation during locomotion

Clearly, the worm is capable of a smooth transition between swimming and crawling waveforms, which must surely involve some underlying change in the pattern of neuromuscular activity. It is therefore interesting to ask whether, in so doing, the worm is responding to internal constraints, e.g., as would be expected if it became power limited.

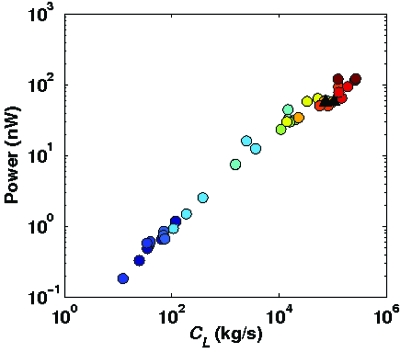
While power dissipation cannot be directly estimated from our recordings (as it requires a knowledge of the magnitudes of resistive forces of the environment, not just the ratio K), a crude approximation can be obtained under two assumptions, first that the viscoelastic model of the environment is a valid approximation (i.e., neglecting other dissipative forces) and, second, that the frequency dependence in such environments is similar to that observed by Korta et al. (2007) in a near-Newtonian medium. Though approximate, the power estimates we obtain (see Methods for more details) indicate that the worm is not power limited (Fig. 3), in agreement with previous results in the nematode (Alexander, 2002) and C. elegans (Korta et al., 2007) literature.

Figure 3. Estimated power dissipation due to resistive drag (see Methods).

Agar data are represented by black triangles, while filled circles show gelatin data. Different colors represent different gelatin concentrations.

Gel media are adequately described by a single-parameter model

As with the theory of Gray and Lissmann (1964), our simulator models the low Reynolds number environmental forces in terms of local resistance coefficients for normal and longitudinal motion. In both works it is the ratio K, in conjunction with the locomotion waveform, that determines the actual motion of the worm. However, it is clear that this model only approximates the properties of gels and complex fluids. To assess the validity of this approximation, we compared the simulated center of mass motion of the worm (for the optimal value of K) to the corresponding experimental trajectory and computed the percent error for each time step of the simulation. We find that the error is generally small, but that large spikes occur at irregular intervals (due to noise in the experimental center of mass recordings). For example, for worms moving on agar or in 2% gelatin, we find that, on average, 81% of simulation time steps have an error of less than 2%, while 91% have an error of less than 5%. We conclude that, indeed, C. elegans locomotion in gelatin and agar environments is adequately described by a single-parameter viscoelastic model of the environment.

DISCUSSION

The primary result of this work is the demonstration of a smooth and continuous change between the so-called swimming and crawling waveforms, indicating that the whole range of behaviors corresponds to a single gait. In the C. elegans literature, however, swimming (often dubbed thrashing) is typically described as having a C-shape as distinct from the S-shape associated with “crawling” (Pierce-Shimomura et al., 2008). This suggests a McNeill Alexander standing-wave buckling motion and is consistent with the two-gait assumption . By demonstrating a smooth transition, our work reveals that swimming and crawling are not qualitatively different and that the observed C-shapes, rather than being universal, are simply the extreme phases of an S-shaped travelling wave with a wavelength longer than the worm’s body. Indeed, Purcell’s scallop theorem (Purcell, 1977) teaches us that any waveform that is invariant under time reversal (as a C-shaped buckling motion would be) cannot propel a body in low Reynolds number environments. Our finding is therefore consistent with recent evidence that the worm can perform goal-directed locomotion even when “swimming” in water (Pierce-Shimomura et al., 2008).

Clearly the worm can (or must) change its locomotion waveform when subjected to different environments. Yet it remains unclear what properties of the environment are relevant and how this information is integrated to adapt the locomotion pattern. The accumulating evidence suggests that for both swimming and crawling, frequency but not wavelength has been observed to change under a variety of conditions (Sawin et al., 2000; Korta et al., 2007). In contrast, here we show that (1) for environments with varying viscoelastic properties (and hence variable K), wavelength and frequency both change and are linearly related; and (2) for flat, non-deformable surfaces where nearly isotropic frictional forces appear to dominate (i.e., K≈1) the worm can nonetheless generate a slow, short wavelength (crawling) undulation pattern. We considered the possibility that the change in waveform is simply a power saturation effect, but our estimates of power dissipation show no sign of approaching a limit, suggesting that this is not the case.

In conclusion, we have extended the traditional approach to studying the locomotion control system of C. elegans by pursuing a more detailed understanding of the environment in which the animal moves. We have demonstrated both that the “crawling” waveform can be produced in the total absence of a groove, and that the physical properties of the groove, when it exists, are insufficient to support the sinusoidal shape of the body. Thus, the motion of the head on its own cannot determine the body shape. Rather the contractions along the body of the worm must be strong and extensive enough to do so, as predicted, for example, in previous work (Bryden and Cohen, 2004, 2008). Furthermore, we have shown that changing the viscoelastic properties of the environment results in a smooth and continuous range of locomotory behaviors, corresponding to a single gait. Thus, while swimming and crawling may involve different patterns of motor control, these differences are only quantitative. The linear relationships among wavelength, frequency, and amplitude compactly capture this smooth modulation of a single class of behaviors. Taken together, our findings unveil a surprising sophistication of the underlying control system. Specifically, our unified description of swimming and crawling poses a clear and focused challenge to the complete and integrated modeling of this complex system.

MATERIALS AND METHODS

Worm culture and behavioral assay

Wild type N2 C. elegans worms were cultivated using standard methods (Brenner, 1974). Experiments were performed on young adult hermaphrodites (4 days from hatching) at 20 °C. Gelatin (SIGMA G-8150) was dissolved in M9 and diluted to the required concentration. 2.5% (v∕v) of swelled Sephadex (G-50 Medium MP Biomedicals 195580) was added to each sample to maintain the space between glass slide and coverslip at 200 μm. Gelatin solution filled the space between slide and coverslip, containing a single worm. A moist dialysis membrane placed on a 2% agar gel pad was used for flat surface experiments. Worms were recorded at 25 frames∕second. Worm midlines were extracted using specially developed “skeletonizer” software. Midlines and worm coordinates were also fed to the physics simulator (see below) to obtain estimates of K.

Skeletonizer

All image analysis relied on a specially developed “skeletonizer” program written in Matlab (MathWorks) to extract sequences of worm body midlines (“skeletons”) from locomotion movies. The algorithm is schematically described in Supplemental Fig. S1. For each frame of the movie, the first step of the algorithm is adapted from Baek et al. (2002) and approximates the location and rough outline of the worm. However, instead of “shrinking” the binarized image of the worm, as done in most skeletonizers, our algorithm uses the original gray scale image to obtain the body midline. The rough binary outline is used to obtain an initial point near the middle of the worm, and the line perpendicular to the body’s local orientation at this point is found. The gray scale intensity profile along this perpendicular is filtered using a Gaussian-derivative kernel yielding the two edges of the profile. The skeleton point is taken to be midway between the two edges, correcting the initial estimate. The process is iterated for points on either side of the starting point (towards head and tail). A minimum intensity threshold criterion (for the filtered intensity profile) is applied to determine the termination points. N=25 equidistant points are then interpolated along this midline. This method has several advantages over those that obtain the body midline by shrinking a black and white image: (1) This method is particularly well suited for detecting worm midlines in low resolution and low contrast images (e.g., worms swimming in liquid imaged with an ordinary webcam and 10× objective). (2) Artifacts due to the use of a shrinking algorithm from a binary image are avoided. In particular, shrinking may lead to (a) skeletons that do not reach the head∕tail and are therefore shorter than the real worm, and (b) branching of the skeleton along the body. (3) This method does not require spline interpolation of the pixels, reducing the risk of artifacts.

Data analysis

Wavespeed, wavelengths and frequency were obtained as described by Korta et al. (2007). Note that the “wavelength” obtained both here and by Korta et al. follows the definition given in the text and corresponds to the arc length along the worm’s body spanning exactly one period. The conventional wavelength is the straight line connecting the extremes of a wave spanning exactly one period (Supplemental Fig. S2).

Reynolds number

All experiments are performed in the low Reynolds number regime. In our Newtonian media (water or M9 buffer), the Reynolds number is highest: Re=vL∕ν≈1 where v is the worm’s velocity (≈1 mm∕s), L is the length of the worm (1 mm), and ν is the kinematic viscosity (≈1 mm²∕s in room temperature water). In viscoelastic environments, the higher effective viscosity and slower motion will yield significantly lower Reynolds numbers.

ESTIMATING K: PHYSICS SIMULATOR

Although we performed a rheological characterization of the range of gelatin concentrations we used, the factor K is unfortunately not measurable by rheological means. Indeed K is particularly hard to estimate experimentally since bulk measurements are not appropriate due to a variety of complicating factors, including the heterogeneity of the gelatin solutions, possible wall effect due to the slides, and the small size of the worm. Instead, we estimate K using our physics simulator. Given an initial guess for K, we solve the equations of motion for the recorded sequence of body shapes and compare the progress (translation and rotation of the center of mass) of the simulated worm to that of the actual worm in the original recording. We can then adjust the value of K according to the discrepancy, repeating this process until the best fit value of K is obtained.

Setup

Worms are recorded at 25 frames∕second (fps) and midlines extracted to obtain the time sequence of coordinates of N equidistant points along the body. Spline interpolation over time was used to upsample the time series to 1000 fps. In each frame the midline is displaced∕rotated such that the center of mass (CoM) is stationary and the head is to the left, yielding a time series of body midlines s(t)={x(t),y(t)}.

Simulation

Our simulation, like the motion of the real worm, is two dimensional. While the body is represented by a 1D curve embedded in this 2D space, the shape of the worm is taken into account by scaling the local drag coefficients for each of the N points according to the diameter of the worm at that point along the body. For an input sequence s(t) and a given value of K, the simulation proceeds as follows. For each time step, the velocities of the N points are resolved into normal and longitudinal components, which evoke reactive environmental forces. Since inertia is negligible, the net external force acting on the worm must at all times be zero. We therefore obtain the CoM translation and rotation giving zero net force and torque over the time step in question. Repeating this process and combining these small displacements gives the CoM trajectory, corresponding to the solution of the equations of motion for the sequence of shapes in question.

Validation against theory

To validate the software, simulations were run in a variety of virtual environments (with K ranging from 1 to 10⁴) using artificially generated sinusoidal midlines with variable wavelength and amplitude. Resulting CoM speeds (v_CoM) were compared to the theory of Gray and Lissmann (1964) using

$$v_{\mathrm{CoM}}=v_{\text{wave}}\frac{B(K-1)}{KB+1},$$ (1)

where v_wave=fλ_conv refers to the wavespeed of undulations (projected onto the axis of the worm’s motion) and $B=2{\pi }^2{A}^2∕{\lambda }_{\mathrm{conv}}^2$ is a property of the amplitude A and conventional wavelength λ_conv. Note that λ_conv is different from the physiological wavelength defined earlier and follows the conventional definition of wavelength.

We find that for low amplitude sinusoidal midlines spanning multiple wavelengths (specifically λ_conv=0.125L, A=0.016λ_conv), the average error per undulation cycle between the simulated and theoretical CoM velocities is at most 0.73% (for K=1.5) and improves slightly with increasing K. For K>20 the error is less than 0.6%.

Numerical results versus simplified analytical treatment

By making certain mathematical simplifications, Gray and Lissmann (1964) were able to derive a mathematical expression relating CoM velocity to the locomotion wave properties (λ,A,F) and the ratio K [Eq. 1]. This expression could easily be rewritten to give K as a function of v_CoM, v_wave, and B, all of which could be obtained from experimental recordings. So why then do we use the admittedly more laborious approach of estimating K from simulations? The reason is that in order to derive their analytical results, Gray and Hancock (1955) made several assumptions: first, that the locomotion wave is sinusoidal; second, that the wavelength λ is short compared to the body length L; and, third, that the amplitude A is sufficiently small that λ≈λ_conv. The simulator, on the other hand, makes no such assumptions about waveform.

Having found close agreement between our simulator and Eq. 1 under certain conditions, we now use the simulator to assess the scope of validity of the simplified analytical treatment. Simulations were performed for a range of K values using locomotion waveforms that (i) have larger, more realistic amplitude [Supplemental Fig. S3(a)], (ii) that deviate from perfect sinusoids and better match the observed shapes of the worm [Supplemental Fig. S3(b)], and (iii) span less than a complete wavelength [as observed in sufficiently dilute gelatin or water, Supplemental Fig. S3(c)].

We find that all of these changes lead to greater discrepancies between theory and simulation, due to the limited applicability of the theory. Specifically, when the waveform deviates from a sine wave in such a way that the wavelength increases towards the tail (as in the real worm), v_wave ceases to be constant along the worm. In high K environments, the maximum λ dominates while for lower K the average λ is more meaningful. Higher amplitude waves introduce errors, particularly in the low K regime, where B dominates in Eq. 1. Shapes spanning less than a wavelength also pose a problem for the theory. This can be explained by considering an extreme case where λ→∞. While this would imply v_wave=fλ_conv→∞, and therefore infinite velocity, the body will actually be a straight line at all times, and no motion will result. Thus, we conclude that for realistic body shapes across a range of K values, a physics simulator is best suited to estimate K.

Estimating power dissipation

The physical simulator was used to estimate power dissipation due to resistive drag. Viscoelastic drag forces give rise to power dissipation of the form

$$P\left(t\right)=C_L{v}_L^2\left(t\right)+C_N{v}_N^2\left(t\right),$$

where C_L,C_N are the drag coefficients, v_L,v_N are the velocities, and the subscripts L and N indicate the longitudinal and normal direction to the local body surface, respectively. Given either C_L or C_N and our estimate of K, it is therefore possible to integrate the power over the length of the worm and over time. Results in Fig. 3 are calculated by estimating C_L from the frequency∕viscosity relationship in Korta et al. (2007).

Rheological characterization of gelatin

The viscoelastic properties of gelatin solutions were measured with a stress-controlled rheometer (Rheometrics DSR 500) equipped with cone and plate fixtures (40 mm plate diameter, 0.04 rad cone angle). A thermo-bath unit guaranteed constant temperature measurements at 20 °C with ±0.1 °C accuracy. Molten gelatin solutions were loaded in the rheometer and then cooled down to the measuring temperature. The temperature equilibration process was monitored with linear oscillatory test at 10 rad∕s. The elastic and loss modulus, G^′ and G^″, of gelatin solutions were measured over a frequency (ω) range of 0.1–100 rad∕s.

For gelatin concentrations <0.8%w∕v, the solutions exhibited viscoelastic behavior, while higher concentration solutions formed gels [i.e., G^′ and G^″ almost frequency independent (Rubinstein and Colby, 2003)]. The results of our characterization are shown in Supplemental Fig. S4. Note that these rheological experiments are conducted on intact solutions, where gels form above a certain concentration. However, in actual locomotion experiments the worm travels through the medium, breaking up the network or molecular mesh making up the gel. Thus, as demonstrated by the validation of the physical simulator, the immediate environment of the worm is effectively viscoelastic for the entire range of gelatin concentrations.

SUPPORTING INFORMATION

Supplementary Movie S1.

Flat surface (dialysis membrane)

Supplementary Movie S2.

Liquid

Supplementary Movie S3.

1.2% gelatin

Supplementary Movie S4.

1.5% gelatin

Supplementary Movie S5.

2.0% gelatin