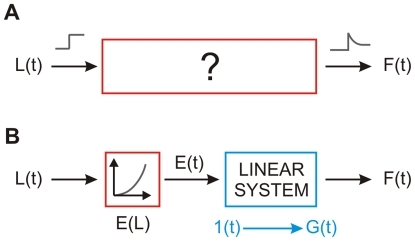
Figure 1. Schematic view of Fung's theory.

A: In most biological passive materials, a stepwise change in elongation (gray trace on the left) causes the force to suddenly increase and then decay over time (gray trace on the right). B: Fung proposed that this response scales with the size of the step, and that there is a nonlinear relationship E(L) between the peak force and the step size (which he called elastic response). He also posited that the decaying response is generated by a linear system, which can be described in terms of its step response. G(t) is then the response of the linear subsystem to a unitary step, 1(t), of the elastic response. This is a cascade of a static nonlinearity and a linear system, often referred to as a Hammerstein system. The model is not limited to reproducing the response to a strain step, but can be used to predict the response to an arbitrary strain history. Blue blocks indicate linear processes, whereas red blocks indicate the presence of a nonlinearity.