Table 4.

Results from a simulation study on 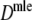for a range of values of genetic similarity p_gs and expected numbers of fragments m₁ and m_2, 10,000 replicated pairs of AFLP profiles, 1,000 bootstrap resamples, fldF_S from A. thaliana with N = 450

Parameter settings			Results for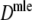
					Wald ci		Profile likelihood ci		Back transformed Wald ci
pgs	m1	m2	Mean	SE	Non-coverage% (too low, too high)	Length	Non-coverage% (too low, too high)	Length	Non-coverage % (too low, too high)	Length
0.0	40	40	0.0202	0.0759	0.59 (0.59)	0.1689	1.98 (1.98)	0.1401	–	–
	70	70	0.0203	0.0651	1.18 (1.18)	0.1477	2.35 (2.35)	0.1275	–	–
	120	120	0.0216	0.0611	1.48 (1.48)	0.1409	2.26 (2.26)	0.1236	–	–
0.1	40	40	0.1004	0.0721	2.41 (0.97, 1.44)	0.2320	4.49 (2.40, 2.09)	0.2364	5.28 (0, 5.28)	0.4532
	70	70	0.1006	0.0645	3.13 (1.25, 1.88)	0.2144	4.64 (2.29, 2.35)	0.2164	5.51 (0, 5.51)	0.3974
	120	120	0.1001	0.0611	3.06 (0.94, 2.12)	0.2056	4.94 (2.59, 2.35)	0.2059	5.80 (0, 5.80)	0.3742
0.3	40	40	0.2979	0.0807	6.27 (3.56, 2.71)	0.3151	5.23 (2.70, 2.53)	0.3074	3.56 (0.02, 3.54)	0.3123
	70	70	0.2987	0.0690	5.77 (2.81, 2.96)	0.2702	5.24 (2.52, 2.72)	0.2660	3.81 (0.15, 3.66)	0.2670
	120	120	0.2985	0.0622	5.43 (2.69, 2.74)	0.2436	5.08 (2.63, 2.45)	0.2411	3.90 (0.24, 3.66)	0.2410
0.5	40	40	0.4978	0.0777	5.54 (2.09, 3.45)	0.3045	4.73 (2.42, 2.31)	0.2948	4.09 (1.40, 2.69)	0.2955
	70	70	0.4978	0.0643	5.29 (2.06, 3.23)	0.2519	4.90 (2.36, 2.54)	0.2495	4.38 (1.51, 2.87)	0.2467
	120	120	0.4981	0.0560	5.08 (2.21, 2.87)	0.2195	4.99 (2.74, 2.25)	0.2183	4.36 (1.76, 2.60)	0.2161
0.7	40	40	0.6974	0.0646	6.24 (1.66, 4.58)	0.2532	6.39 (3.56, 2.83)	0.2363	4.72 (2.35, 2.37)	0.2492
	70	70	0.6989	0.0523	5.53 (1.75, 3.78)	0.2049	5.01 (2.55, 2.46)	0.2030	4.56 (2.35, 2.21)	0.2028
	120	120	0.6987	0.0445	5.67 (1.65, 4.02)	0.1744	5.20 (2.43, 2.77)	0.1741	4.88 (2.20, 2.68)	0.1731
0.9*	40	40	0.8976	0.0382	7.74 (0.70, 7.04)	0.1496	12.60 (9.95, 2.65)	0.1301	3.77 (3.04,0.73)	0.1582
	70	70	0.8995	0.0304	6.96 (0.87, 6.09)	0.1192	7.76 (5.14, 2.62)	0.1092	4.24 (2.88, 1.36)	0.1238
	120	120	0.8997	0.0255	6.83 (1.05, 5.78)	0.0999	5.30 (2.50, 2.80)	0.0990	4.54 (2.87, 1.67)	0.1026
0.95*	40	40	0.9491	0.0266	13.42 (0.22, 13.20)	0.1007	19.34 (15.61, 3.73)	0.0899	6.43 (2.95, 3.48)	0.1199
*	70	70	0.9496	0.0208	9.96 (0.46, 9.50)	0.0817	12.87 (9.48, 3.39)	0.0736	3.73 (3.20, 0.53)	0.0923
*	120	120	0.9500	0.0175	9.06 (0.75, 8.31)	0.0684	6.47 (3.42, 3.05)	0.0659	4.10 (3.08, 1.02)	0.0750
0.5	100	50	0.4977	0.0592	5.56 (2.35, 3.21)	0.2320	5.23 (2.66, 2.57)	0.2301	4.71 (1.86, 2.85)	0.2280
0.5	100	80	0.4982	0.0595	5.36 (2.30, 3.06)	0.2330	4.88 (2.57, 2.31)	0.2314	4.54 (1.84, 2.70)	0.2289
0.7	70	40	0.6980	0.0544	5.96 (1.67, 4.29)	0.2132	5.65 (2.77, 2.88)	0.2054	4.97 (2.34, 2.62)	0.2109
0.7	80	70	0.6985	0.0509	5.75 (2.62, 2.21)	0.1995	5.20 (2.84, 2.36)	0.1983	4.83 (2.62, 2.21)	0.1976

Shown are the mean, mean standard error, and properties of three types of confidence intervals: non-coverage percentage (with left and right non-coverage percentages), and mean length of (1) 95% Wald c.i., (2) 95% profile likelihood c.i., and (3) 95% logit-back transformed Wald c.i. At p_gs = 0.0, only non-coverage at the right of p_gs = 0.0 is considered

* In case p_gs = 0.9 (m = 40), or p_gs = 0.959 (m = 40, 70, 120) identical pairs of profiles were sampled (10, 348, 53, and 10 times, respectively); in these cases 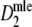 = 1, with standard error 0, and we took logit(p_c) = 16 with standard error 0